1.3.2 证明的表达格式 课件(共12张PPT)
文档属性
| 名称 | 1.3.2 证明的表达格式 课件(共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
浙教版
八年级上
1.3
证明
第2课时
证明的表达格式
新知导入
什么是证明?
要判定一个命题是真命题,往往需要从命题的条件出发,
根据已知的定义、基本事实、定理,一步一步推出结论成立,
这样的推理过程叫做证明.
新知讲解
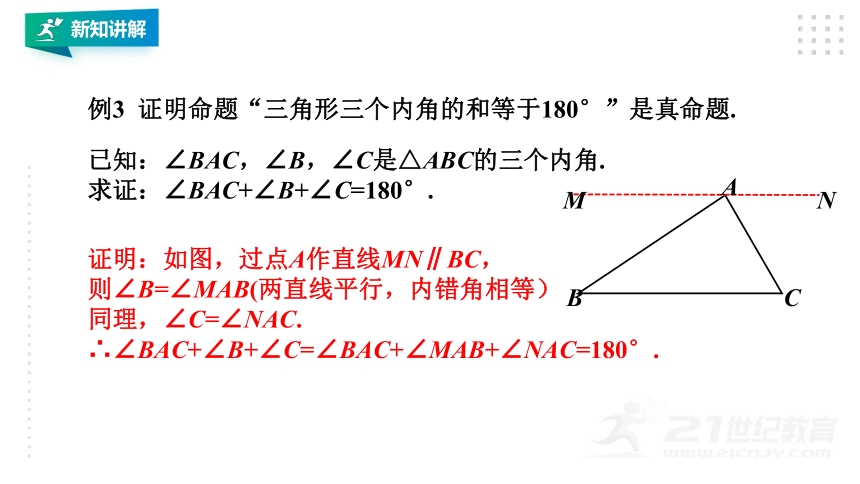
证明:如图,过点A作直线MN∥BC,
则∠B=∠MAB(两直线平行,内错角相等)
同理,∠C=∠NAC.
∴∠BAC+∠B+∠C=∠BAC+∠MAB+∠NAC=180°.
A
B
C
M
N
例3
证明命题“三角形三个内角的和等于180°”是真命题.
已知:∠BAC,∠B,∠C是△ABC的三个内角.
求证:∠BAC+∠B+∠C=180°.
新知讲解
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边CA组成的角,这样的角叫做该三角形的外角.
三角形的外角等于与它不相邻的两个内角的和.
∵∠ACD+∠ACB=180°,
且∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠B.
A
B
C
D
这是由三角形的内角和定理直接推理得到的一个推论.
推论也可以作为推理的依据.
新知讲解
证明几何命题时,表述格式一般是:
(1)按题意画出图形;
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,
在“求证”中写出结论;
(3)在“证明”中写出推理过程.
为了使我们的解答更为规范和有条理,请同学们总结一下
证明一个命题的一般步骤.
新知讲解
例4
已知:如图,∠B+∠D=∠BCD.求证:AB∥DE.
分析:如图,延长BC,交DE于点F.
根据平行线的判定定理,只要证明∠B=∠CFD,
或∠B+∠BFE=180°,就能证明AB∥DE.
A
B
C
D
E
F
证明:如图,延长BC,交DE于点F.
∵∠B+∠D=∠BCD(已知),
又∵∠BCD=∠D+∠CFD
(三角形的外角等于与它不相邻的两个内角的和),
∴∠B+∠D=∠D+∠CFD,
∴∠B=∠CFD.
∴AB∥DE(内错角相等,两直线平行).
课堂练习
1.如图,下列关于△ABC的外角的说法正确的是( )
A.∠HBA是△ABC的外角
B.∠HBG是△ABC的外角
C.∠DCE是△ABC的外角
D.∠GBA是△ABC的外角
D
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
C
课堂练习
3.如图,将三角形纸板的直角顶点放在直尺的一边上,
∠1=20°,∠2=40°,则∠3等于( )
A.50°
B.30°
C.20°
D.15°
C
4.如图,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
B
课堂练习
拓展提高
5.如图,已知∠BDC=142°,∠B=34°,∠C=28°,
则∠BAC=________.
【提示】连结AD并延长,如图:
∵∠1=∠DAC+∠C,∠2=∠DAB+∠B,
∴∠1+∠2=∠DAC+∠C+∠DAB+∠B,
∴∠BDC=∠BAC+∠B+∠C.
∵∠BDC=142°,∠B=34°,∠C=28°,
∴142°=∠BAC+34°+28°,
∴∠BAC=142°-34°-28°=80°.
中考链接
6.(2020?泰州)如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为
.
140°
中考链接
7.(2018?宜昌)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.求∠CBE的度数.
解:∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°-∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD÷2=65°
课堂总结
(1)三角形内角和定理的证明方法.
(2)三角形外角的性质:
三角形的外角等于与它不相邻的两个内角的和.
(3)常用的几何证明方法:
由结论出发寻求使结论成立的条件,进而形成解题思路.
本节课你学到了什么?
https://www.21cnjy.com/help/help_extract.php
浙教版
八年级上
1.3
证明
第2课时
证明的表达格式
新知导入
什么是证明?
要判定一个命题是真命题,往往需要从命题的条件出发,
根据已知的定义、基本事实、定理,一步一步推出结论成立,
这样的推理过程叫做证明.
新知讲解
证明:如图,过点A作直线MN∥BC,
则∠B=∠MAB(两直线平行,内错角相等)
同理,∠C=∠NAC.
∴∠BAC+∠B+∠C=∠BAC+∠MAB+∠NAC=180°.
A
B
C
M
N
例3
证明命题“三角形三个内角的和等于180°”是真命题.
已知:∠BAC,∠B,∠C是△ABC的三个内角.
求证:∠BAC+∠B+∠C=180°.
新知讲解
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边CA组成的角,这样的角叫做该三角形的外角.
三角形的外角等于与它不相邻的两个内角的和.
∵∠ACD+∠ACB=180°,
且∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠B.
A
B
C
D
这是由三角形的内角和定理直接推理得到的一个推论.
推论也可以作为推理的依据.
新知讲解
证明几何命题时,表述格式一般是:
(1)按题意画出图形;
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,
在“求证”中写出结论;
(3)在“证明”中写出推理过程.
为了使我们的解答更为规范和有条理,请同学们总结一下
证明一个命题的一般步骤.
新知讲解
例4
已知:如图,∠B+∠D=∠BCD.求证:AB∥DE.
分析:如图,延长BC,交DE于点F.
根据平行线的判定定理,只要证明∠B=∠CFD,
或∠B+∠BFE=180°,就能证明AB∥DE.
A
B
C
D
E
F
证明:如图,延长BC,交DE于点F.
∵∠B+∠D=∠BCD(已知),
又∵∠BCD=∠D+∠CFD
(三角形的外角等于与它不相邻的两个内角的和),
∴∠B+∠D=∠D+∠CFD,
∴∠B=∠CFD.
∴AB∥DE(内错角相等,两直线平行).
课堂练习
1.如图,下列关于△ABC的外角的说法正确的是( )
A.∠HBA是△ABC的外角
B.∠HBG是△ABC的外角
C.∠DCE是△ABC的外角
D.∠GBA是△ABC的外角
D
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35°
B.95°
C.85°
D.75°
C
课堂练习
3.如图,将三角形纸板的直角顶点放在直尺的一边上,
∠1=20°,∠2=40°,则∠3等于( )
A.50°
B.30°
C.20°
D.15°
C
4.如图,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
B
课堂练习
拓展提高
5.如图,已知∠BDC=142°,∠B=34°,∠C=28°,
则∠BAC=________.
【提示】连结AD并延长,如图:
∵∠1=∠DAC+∠C,∠2=∠DAB+∠B,
∴∠1+∠2=∠DAC+∠C+∠DAB+∠B,
∴∠BDC=∠BAC+∠B+∠C.
∵∠BDC=142°,∠B=34°,∠C=28°,
∴142°=∠BAC+34°+28°,
∴∠BAC=142°-34°-28°=80°.
中考链接
6.(2020?泰州)如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为
.
140°
中考链接
7.(2018?宜昌)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.求∠CBE的度数.
解:∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°-∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD÷2=65°
课堂总结
(1)三角形内角和定理的证明方法.
(2)三角形外角的性质:
三角形的外角等于与它不相邻的两个内角的和.
(3)常用的几何证明方法:
由结论出发寻求使结论成立的条件,进而形成解题思路.
本节课你学到了什么?
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
