第一章二次根式复习
图片预览




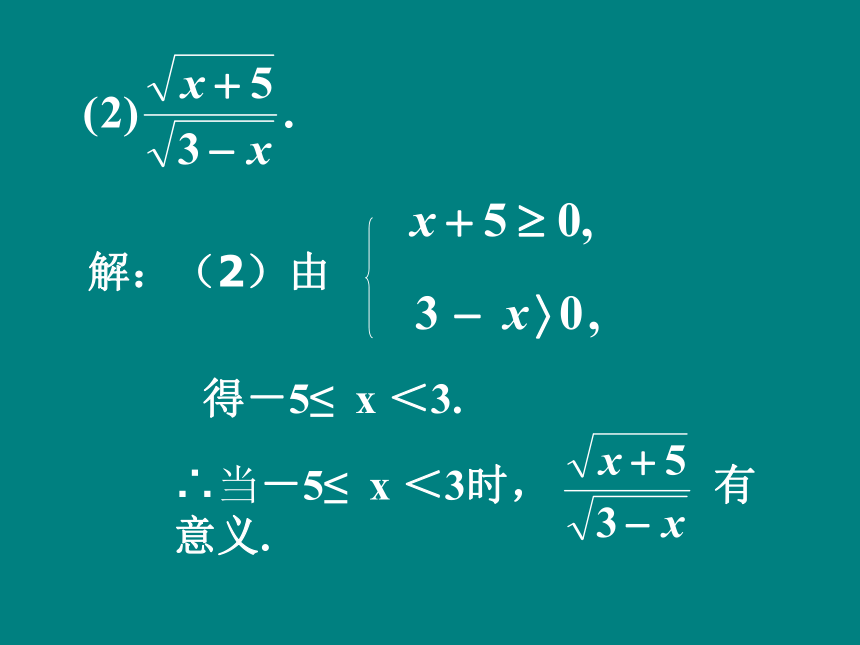


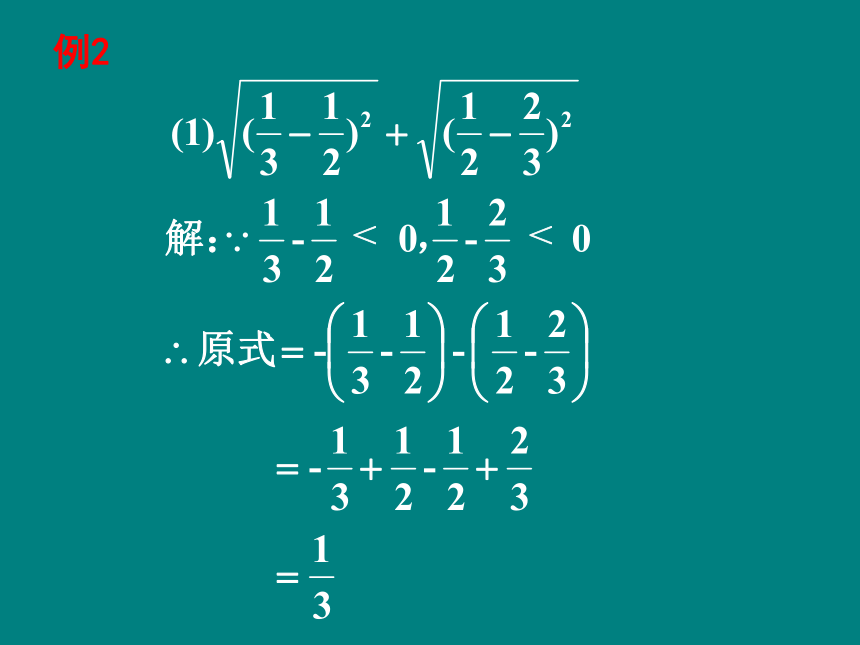
文档简介
(共28张PPT)
第一章 二次根式复习
1.二次根式的概念及意义.
形如 (a≥0 )这样的式子叫做二次根式,其中a可以是数,也可以是单项式和多项式.
知识回顾
①
、
x+3
②
、
2
-
x
③
、
1
x
④
、
a
2
+1
x≥-3
x≤2
x>0
a为全体实数
本领1: 会求字母的取值范围.
注意:
被开方数大于或等于零
例1、x 取何值时,下列各式在实数范围内有意义?
解:(1)由
∴当x≥-1且x≠2时,式子 有意义.
得x≥-1且x≠2.
解:(2)由
得-5≤ x <3.
∴当-5≤ x <3时, 有意义.
练习1:当x取何值时,下列二次根式有意义
试一试:
2.二次根式的四个基本性质
知识回顾
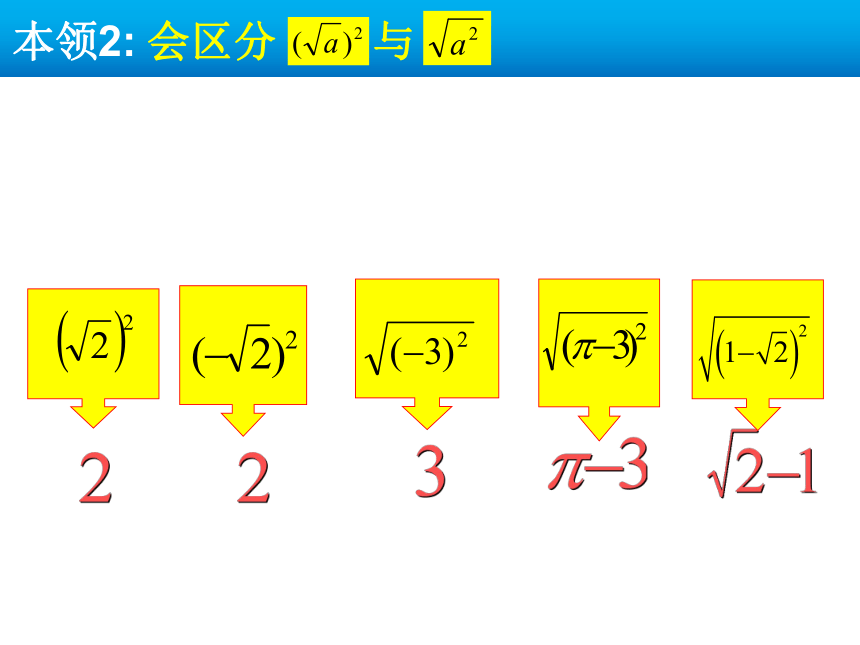
本领2: 会区分 与
例2
<
<
例2
(2) 表示a,b两个实数的点在数轴上的位置如图所
示,化简│a-b│+
<
>
练习2:
已知0试一试:
(3)
(4)
(1)
(2)
(5)
(6)
本领3: 会正确应用性质3、4
例3 计算:
(2)
解:原式
练习3:
试一试:
A
B
P
D
C
若点P为线段CD上动点。
拓展题: 已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C,
①则AD=____ BC=____
1
2
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
A
B
P
D
C
若点P为线段CD上动点。
拓展题: 已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C,
①则AD=____ BC=____
1
2
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
A
B
P
D
C
拓展题3:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题3:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题3:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
已知△ABP的一边AB=
拓展题:
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
1
2
A
B
P
D
C
已知△ABP的一边AB=
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
设DP=a,请用含a的代数式 表示AP,BP。则AP=_____,BP=_____。
当a=3,则PA+PB=____
拓展题:
①则AD=____ BC=____
1
2
②
②
当a=1 时,则PA+PB=____,
③
拓展题:
PA+PB是否存在一个最小值?
④
请你猜一猜
星期天,张明的妈妈和张明做个小游戏,张明的妈妈说:“你现在学习了二次根式,若 表示 的整数部分, 表示它的小数部分,我这个纸包里的钱是 元,你猜一猜这个纸包里的钱数是多少?若猜对了,纸包里的钱全奖给你。”说完,张明很快猜出了他妈妈纸包里的钱?聪明的你知道张明是怎么算的吗?
拓展题:
已知
,
,
变式:
化简:
解:原式=
2
2
=
=
=
= - 2
拓展题:
第一章 二次根式复习
1.二次根式的概念及意义.
形如 (a≥0 )这样的式子叫做二次根式,其中a可以是数,也可以是单项式和多项式.
知识回顾
①
、
x+3
②
、
2
-
x
③
、
1
x
④
、
a
2
+1
x≥-3
x≤2
x>0
a为全体实数
本领1: 会求字母的取值范围.
注意:
被开方数大于或等于零
例1、x 取何值时,下列各式在实数范围内有意义?
解:(1)由
∴当x≥-1且x≠2时,式子 有意义.
得x≥-1且x≠2.
解:(2)由
得-5≤ x <3.
∴当-5≤ x <3时, 有意义.
练习1:当x取何值时,下列二次根式有意义
试一试:
2.二次根式的四个基本性质
知识回顾
本领2: 会区分 与
例2
<
<
例2
(2) 表示a,b两个实数的点在数轴上的位置如图所
示,化简│a-b│+
<
>
练习2:
已知0
(3)
(4)
(1)
(2)
(5)
(6)
本领3: 会正确应用性质3、4
例3 计算:
(2)
解:原式
练习3:
试一试:
A
B
P
D
C
若点P为线段CD上动点。
拓展题: 已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C,
①则AD=____ BC=____
1
2
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
A
B
P
D
C
若点P为线段CD上动点。
拓展题: 已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C,
①则AD=____ BC=____
1
2
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
A
B
P
D
C
拓展题3:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题3:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题3:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
拓展题:已知△ABP的一边AB=
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
1
2
A
B
P
D
C
已知△ABP的一边AB=
拓展题:
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
①则AD=____ BC=____
1
2
A
B
P
D
C
已知△ABP的一边AB=
(1)在如图所示的4×4的方格中画出格点△ABP,使三角形的三边为
(2)如图所示,AD⊥DC于D,BC⊥CD于C, 若点P为线段CD上动点。
设DP=a,请用含a的代数式 表示AP,BP。则AP=_____,BP=_____。
当a=3,则PA+PB=____
拓展题:
①则AD=____ BC=____
1
2
②
②
当a=1 时,则PA+PB=____,
③
拓展题:
PA+PB是否存在一个最小值?
④
请你猜一猜
星期天,张明的妈妈和张明做个小游戏,张明的妈妈说:“你现在学习了二次根式,若 表示 的整数部分, 表示它的小数部分,我这个纸包里的钱是 元,你猜一猜这个纸包里的钱数是多少?若猜对了,纸包里的钱全奖给你。”说完,张明很快猜出了他妈妈纸包里的钱?聪明的你知道张明是怎么算的吗?
拓展题:
已知
,
,
变式:
化简:
解:原式=
2
2
=
=
=
= - 2
拓展题:
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
