1.4 全等三角形 课件(共23张PPT)
文档属性
| 名称 | 1.4 全等三角形 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 21:46:50 | ||
图片预览






文档简介
(共23张PPT)
1.4全等三角形
浙教版
八年级上
新知导入
仔细观察下列各组图形,你发现了什么?
(1)
(2)
(3)
(4)
新知导入
能够重合的两个图形叫做全等图形.
全等图形的形状和大小完全相同.
新知讲解
形状相同,但大小不同,
因此它们不是全等图形.
新知讲解
能够重合的两个三角形叫做全等三角形.
新知讲解
A
B
C
E
D
F
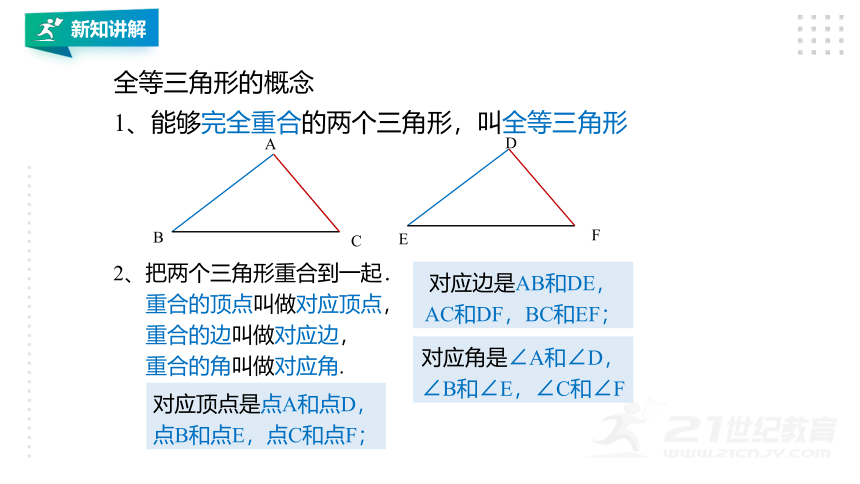
1、能够完全重合的两个三角形,叫全等三角形
2、把两个三角形重合到一起.
重合的顶点叫做对应顶点,
重合的边叫做对应边,
重合的角叫做对应角.
对应顶点是点A和点D,
点B和点E,点C和点F;
对应边是AB和DE,
AC和DF,BC和EF;
对应角是∠A和∠D,
∠B和∠E,∠C和∠F
全等三角形的概念
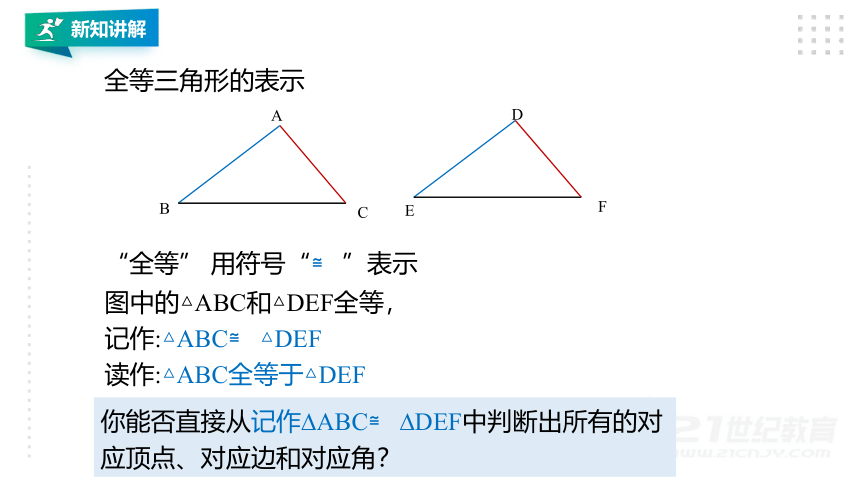
“全等”
用符号“≌
”表示
图中的△ABC和△DEF全等,
记作:△ABC≌
△DEF
读作:△ABC全等于△DEF
你能否直接从记作?ABC≌
?DEF中判断出所有的对应顶点、对应边和对应角?
全等三角形的表示
A
B
C
E
D
F
新知讲解
A
B
C
D
E
F
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
注意:
新知讲解
例题讲解
例1:如图,△ABC≌△DCB,
指出所有的对应边和对应角.
O
D
C
B
A
解:∵△ABC≌△DCB
∴AB与DC,BC与CB,
AC与BD是对应边.
∠A与∠
D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角.
课内练习
O
D
C
B
A
图中△ABO≌△DCO,试写出这两个三角形中相等的边和相等的角.
解:∵△ABO≌△DCO
∴AB=DC,BO=CO,AO=DO
∠A=∠
D,∠ABO=∠DCO,
∠AOB=∠DOC
S
O
T
D
C
N
M
O
A
B
两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?
寻找各图中两个全等三角形的对应元素.
E
A
D
B
F
观察思考
C
全等三角形的对应边相等,对应角相等.
如图:∵△ABC≌
△DFE
∴
AB=DF,BC=FE,AC=DE
∵△ABC≌
△DFE
∴∠A=∠D,
∠B=∠F,∠C=∠E
D
E
F
A
B
C
全等三角形的性质
几何语言:
图形语言:
新知讲解
例2:如图,AD平分∠BAC,AB=AC.
△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说明理由.
解:△ABD≌△ACD
,BD=CD,∠B=∠C
理由如下:
∵
AD平分∠BAC,
∴
∠1=
∠
2,因此将图形沿AD对折时,
射线AB和射线AC重合.
∵AB=AC
,
∴点C和点B重合,
也就是
△ACD与△ABD重合,
∴△ABD
≌
△ACD(全等三角形的定义)
∴BD=CD(全等三角形的对应边相等)
∠B
=
∠C(全等三角形的对应角相等)
A
C
B
D
1
2
例题讲解
课堂小结
1、什么是全等图形、全等三角形、全等三角形的对应顶点、
对应边、对应角?
2、表示三角形全等时应注意什么?
3、识别全等三角形的对应边、对应角的关键是正确识别它们的对应顶点.
4、全等三角形的性质:
全等三角形的对应边相等,对应角相等.
课堂练习
1、选择题
(1)如图,△ABC≌
△BAD,A和B、C和D是对应点,如果
AB=5cm,BD=4cm,AD=6cm,那么BC的长是
(
)
A.
6cm
B.
5cm
C.
4cm
D.
无法确定
(2)在上题中,
∠CAB的对应角是(
)
A.
∠DAB
B.
∠
DBA
C.
∠
DBC
D.
∠
CAD
A
O
C
D
B
A
B
课堂练习
2、判断题:
①全等三角形的对应边相等,对应角相等.(
)
②全等三角形的周长相等.
(
)
③面积相等的三角形是全等三角形.
(
)
④全等三角形的面积相等.(
)
√
√
√
×
课堂练习
A
B
C
D
A
B
C
D
E
4、已知:
△ABC≌△AED请找出右图中对应的角.
3、已知:△ABD≌△CDB.
请找出右图中对应的边.
答案提示:
答案:AB=CD,AD=CB,BD=DB
课堂练习
5、如图,△ABD
≌
△EBC
D
A
B
C
E
(2)如果AB=3cm,BC=5cm,求BE、BD的长.
解:∵△ABD
≌
△EBC
∴AB=EB,BC=BD
∵AB=3cm,BC=5cm
∴BE=3cm,BD=5cm
(1)请找出对应边和对应角.
AB
与
EB、BC与BD、AD与EC,
∠A与∠BEC、∠D与∠C、∠ABD与∠EBC
课堂练习
6、如图,△EFG≌△NMH
解:∵△EFG
≌
△NMH
∴NM=EF=2.1cm,EG=HN=3.3cm
∴HG=EG-HG=3.3-1.1=2.2(cm)
(1)请找出对应边和对应角.
(2)如果EF=2.1cm,EH=1.1cm,HN=3.3cm,
求NM、HG的长.
N
M
F
G
E
H
7、△ABD≌△ACE,若∠ADB=100°,∠B=30°,说出△ACE中各角的大小?
解:∵
△ABD≌△ACE,
∴∠AEC=
∠ADB=100°
,
∠C=
∠B=30°,
又∵∠A+∠AEC+∠C=180
°
∴∠A=180
°
-
∠AEC-
∠C
=180
°
-100
°
-30
°
=50
°
B
C
D
E
A
课堂练习
作业布置
作业本
课本作业题1.2.4
https://www.21cnjy.com/help/help_extract.php
1.4全等三角形
浙教版
八年级上
新知导入
仔细观察下列各组图形,你发现了什么?
(1)
(2)
(3)
(4)
新知导入
能够重合的两个图形叫做全等图形.
全等图形的形状和大小完全相同.
新知讲解
形状相同,但大小不同,
因此它们不是全等图形.
新知讲解
能够重合的两个三角形叫做全等三角形.
新知讲解
A
B
C
E
D
F
1、能够完全重合的两个三角形,叫全等三角形
2、把两个三角形重合到一起.
重合的顶点叫做对应顶点,
重合的边叫做对应边,
重合的角叫做对应角.
对应顶点是点A和点D,
点B和点E,点C和点F;
对应边是AB和DE,
AC和DF,BC和EF;
对应角是∠A和∠D,
∠B和∠E,∠C和∠F
全等三角形的概念
“全等”
用符号“≌
”表示
图中的△ABC和△DEF全等,
记作:△ABC≌
△DEF
读作:△ABC全等于△DEF
你能否直接从记作?ABC≌
?DEF中判断出所有的对应顶点、对应边和对应角?
全等三角形的表示
A
B
C
E
D
F
新知讲解
A
B
C
D
E
F
记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
注意:
新知讲解
例题讲解
例1:如图,△ABC≌△DCB,
指出所有的对应边和对应角.
O
D
C
B
A
解:∵△ABC≌△DCB
∴AB与DC,BC与CB,
AC与BD是对应边.
∠A与∠
D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角.
课内练习
O
D
C
B
A
图中△ABO≌△DCO,试写出这两个三角形中相等的边和相等的角.
解:∵△ABO≌△DCO
∴AB=DC,BO=CO,AO=DO
∠A=∠
D,∠ABO=∠DCO,
∠AOB=∠DOC
S
O
T
D
C
N
M
O
A
B
两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?
寻找各图中两个全等三角形的对应元素.
E
A
D
B
F
观察思考
C
全等三角形的对应边相等,对应角相等.
如图:∵△ABC≌
△DFE
∴
AB=DF,BC=FE,AC=DE
∵△ABC≌
△DFE
∴∠A=∠D,
∠B=∠F,∠C=∠E
D
E
F
A
B
C
全等三角形的性质
几何语言:
图形语言:
新知讲解
例2:如图,AD平分∠BAC,AB=AC.
△ABD与△ACD全等吗?BD与CD相等吗?∠B与∠C呢?请说明理由.
解:△ABD≌△ACD
,BD=CD,∠B=∠C
理由如下:
∵
AD平分∠BAC,
∴
∠1=
∠
2,因此将图形沿AD对折时,
射线AB和射线AC重合.
∵AB=AC
,
∴点C和点B重合,
也就是
△ACD与△ABD重合,
∴△ABD
≌
△ACD(全等三角形的定义)
∴BD=CD(全等三角形的对应边相等)
∠B
=
∠C(全等三角形的对应角相等)
A
C
B
D
1
2
例题讲解
课堂小结
1、什么是全等图形、全等三角形、全等三角形的对应顶点、
对应边、对应角?
2、表示三角形全等时应注意什么?
3、识别全等三角形的对应边、对应角的关键是正确识别它们的对应顶点.
4、全等三角形的性质:
全等三角形的对应边相等,对应角相等.
课堂练习
1、选择题
(1)如图,△ABC≌
△BAD,A和B、C和D是对应点,如果
AB=5cm,BD=4cm,AD=6cm,那么BC的长是
(
)
A.
6cm
B.
5cm
C.
4cm
D.
无法确定
(2)在上题中,
∠CAB的对应角是(
)
A.
∠DAB
B.
∠
DBA
C.
∠
DBC
D.
∠
CAD
A
O
C
D
B
A
B
课堂练习
2、判断题:
①全等三角形的对应边相等,对应角相等.(
)
②全等三角形的周长相等.
(
)
③面积相等的三角形是全等三角形.
(
)
④全等三角形的面积相等.(
)
√
√
√
×
课堂练习
A
B
C
D
A
B
C
D
E
4、已知:
△ABC≌△AED请找出右图中对应的角.
3、已知:△ABD≌△CDB.
请找出右图中对应的边.
答案提示:
答案:AB=CD,AD=CB,BD=DB
课堂练习
5、如图,△ABD
≌
△EBC
D
A
B
C
E
(2)如果AB=3cm,BC=5cm,求BE、BD的长.
解:∵△ABD
≌
△EBC
∴AB=EB,BC=BD
∵AB=3cm,BC=5cm
∴BE=3cm,BD=5cm
(1)请找出对应边和对应角.
AB
与
EB、BC与BD、AD与EC,
∠A与∠BEC、∠D与∠C、∠ABD与∠EBC
课堂练习
6、如图,△EFG≌△NMH
解:∵△EFG
≌
△NMH
∴NM=EF=2.1cm,EG=HN=3.3cm
∴HG=EG-HG=3.3-1.1=2.2(cm)
(1)请找出对应边和对应角.
(2)如果EF=2.1cm,EH=1.1cm,HN=3.3cm,
求NM、HG的长.
N
M
F
G
E
H
7、△ABD≌△ACE,若∠ADB=100°,∠B=30°,说出△ACE中各角的大小?
解:∵
△ABD≌△ACE,
∴∠AEC=
∠ADB=100°
,
∠C=
∠B=30°,
又∵∠A+∠AEC+∠C=180
°
∴∠A=180
°
-
∠AEC-
∠C
=180
°
-100
°
-30
°
=50
°
B
C
D
E
A
课堂练习
作业布置
作业本
课本作业题1.2.4
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
