2.1.2 有理数的加法 课件(共16张PPT)
文档属性
| 名称 | 2.1.2 有理数的加法 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-04 14:32:38 | ||
图片预览






文档简介
(共16张PPT)
2.1有理数的加法
第2课时
浙教版
七年级上
新知导入
比一比,看谁算得快!
你运用了什么方法使计算简便?
加法交换律和结合律
新知导入
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
这两条运算律在有理数范围内还成立吗?
合作探究
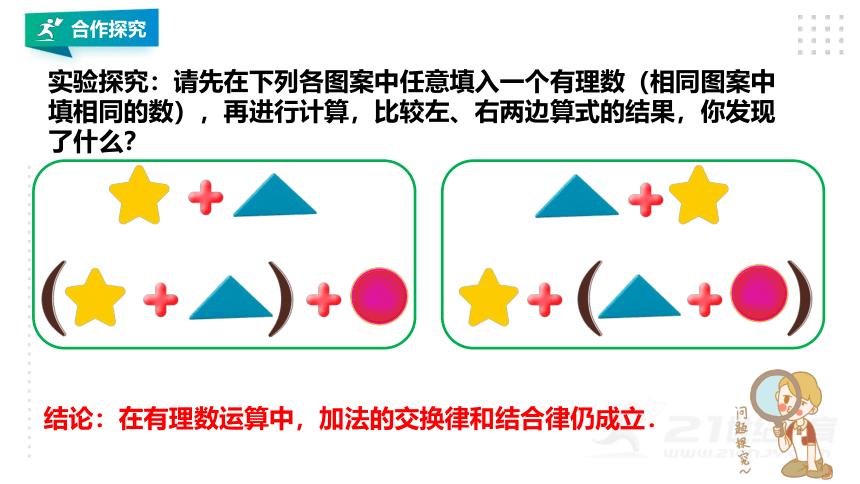
实验探究:请先在下列各图案中任意填入一个有理数(相同图案中填相同的数),再进行计算,比较左、右两边算式的结果,你发现了什么?
结论:在有理数运算中,加法的交换律和结合律仍成立.
新知讲解
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
a+b=b+a
(a+b)+c=a+(b+c)
更一般地,任意若干个数相加,无论各数相加的先后次序如何,其和都不变.
文字语言
符号语言
文字语言
符号语言
例题分析
例1
先读算式,然后计算:
(1)15+(-13)+18
(2)(-2.48)+4.33+(-7.52)+(-4.33)
(3)+
(-
)+(-
)+(-
)
原式=+18+(-13)
=(15+18)+(-13)
=33+(-13)
=20
原式=(-2.48)+(-7.52)+
4.33
+(-4.33)
=[(-2.48)+(-7.52)]+[
4.33
+(-4.33)]
=(-10)+0
=-10
原式=+
=
+(-1)
=-
1.同号结合
2.凑整(十)
3.同分母结合
4.带号换位
课堂练习
1.计算:
(1)5+(-7)+8
(2)(-
)+
+(-
)
(3)(-3.5)+[3+(-1.5)]
答案:6
答案:-
答案:
-2
课堂练习
2.用简便方法计算:
(1)(+14)+(-4)+(-1)+(+16)+(-5)
(2)(-18.65)+(-7.25)+(+18.15)+(+7.25)
(3)(-2.25)+(-
)+(-
)+(+0.125)
答案:20
答案:-0.5
答案:-3
例题分析
例2
小明遥控一辆玩具赛车,让它从A点出发,先向东行驶15m,再向西行驶25m,然后又向东行驶20m,再向西行驶35m,问玩具赛车最后停在何处?一共行驶了多少米?
?5
0
5
10
15
?10
?15
?20
?25
20
?30
15
-25
20
-35
东
西
你可以画一个示意图表示行驶过程吗?
思考1:
例题分析
例2
小明遥控一辆玩具赛车,让它从A点出发,先向东行驶15m,再向西行驶25m,然后又向东行驶20m,再向西行驶35m,问玩具赛车最后停在何处?一共行驶了多少米?
?5
0
5
10
15
?10
?15
?20
?25
20
?30
15
-25
20
-35
东
西
你可以列算式解决这个问题吗?
思考2:
和方向有关
和方向无关
解:(+15)+(-25)+(+20)+(-35)
=(15+20)+[(-25)+(-35)]
=35+(-60)
=-25(m)
|+15|+|-25|+|+20|+|-35|
=15+25+20+35
=95(m)
答:玩具赛车最后停在点A西面25m处,一共行驶了95m.
课堂练习
3.出租车司机小张某天的营运全是在东西走向的大道上进行的,规定向东为正,向西为负,他这天的行程(单位:km)是:+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距离出发点多少千米?在出发点的什么方向?
(2)已知汽车耗油量为0.6
L/km,出发时,油箱有油72.2
L.若小张将最后一名乘客送达目的地,再返回出发点.问:小张返回时是否需要加油?若要加油,至少要加多少油才能返回出发点?若不用加油,请说明理由.
(1)(+15)+(-3)+(+16)+(-11)+(+10)+(-12)+(+4)+(-15)+(+16)+(-18)
=2(km)
答:小张距离出发点2
km,在出发点的东面.
(2)|+15|+|-3|+|+16|+|-11|+|+10|+|-12|+|+4|+|-15|+|+16|+|-18|
=122(km)
所需油量:
122×0.6=73.2(L)
>72.2(L)
∴需要加油
∴至少要加73.2-72.2=1(L)油才能返回出发点.
课堂总结
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
a+b=b+a
(a+b)+c=a+(b+c)
文字语言
符号语言
文字语言
符号语言
1.同号结合
2.凑整(十)
3.同分母结合
4.带号换位
合并技巧:
板书设计
加法交换律:
加法结合律:
a+b=b+a
(a+b)+c=a+(b+c)
1.同号结合
2.凑整(十)
3.同分母结合
4.带号换位
合并技巧:
2.1有理数的加法(2)
作业布置
1.作业本2
2.1有理数的加法(2)
2.自主练习
https://www.21cnjy.com/help/help_extract.php
2.1有理数的加法
第2课时
浙教版
七年级上
新知导入
比一比,看谁算得快!
你运用了什么方法使计算简便?
加法交换律和结合律
新知导入
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
这两条运算律在有理数范围内还成立吗?
合作探究
实验探究:请先在下列各图案中任意填入一个有理数(相同图案中填相同的数),再进行计算,比较左、右两边算式的结果,你发现了什么?
结论:在有理数运算中,加法的交换律和结合律仍成立.
新知讲解
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
a+b=b+a
(a+b)+c=a+(b+c)
更一般地,任意若干个数相加,无论各数相加的先后次序如何,其和都不变.
文字语言
符号语言
文字语言
符号语言
例题分析
例1
先读算式,然后计算:
(1)15+(-13)+18
(2)(-2.48)+4.33+(-7.52)+(-4.33)
(3)+
(-
)+(-
)+(-
)
原式=+18+(-13)
=(15+18)+(-13)
=33+(-13)
=20
原式=(-2.48)+(-7.52)+
4.33
+(-4.33)
=[(-2.48)+(-7.52)]+[
4.33
+(-4.33)]
=(-10)+0
=-10
原式=+
=
+(-1)
=-
1.同号结合
2.凑整(十)
3.同分母结合
4.带号换位
课堂练习
1.计算:
(1)5+(-7)+8
(2)(-
)+
+(-
)
(3)(-3.5)+[3+(-1.5)]
答案:6
答案:-
答案:
-2
课堂练习
2.用简便方法计算:
(1)(+14)+(-4)+(-1)+(+16)+(-5)
(2)(-18.65)+(-7.25)+(+18.15)+(+7.25)
(3)(-2.25)+(-
)+(-
)+(+0.125)
答案:20
答案:-0.5
答案:-3
例题分析
例2
小明遥控一辆玩具赛车,让它从A点出发,先向东行驶15m,再向西行驶25m,然后又向东行驶20m,再向西行驶35m,问玩具赛车最后停在何处?一共行驶了多少米?
?5
0
5
10
15
?10
?15
?20
?25
20
?30
15
-25
20
-35
东
西
你可以画一个示意图表示行驶过程吗?
思考1:
例题分析
例2
小明遥控一辆玩具赛车,让它从A点出发,先向东行驶15m,再向西行驶25m,然后又向东行驶20m,再向西行驶35m,问玩具赛车最后停在何处?一共行驶了多少米?
?5
0
5
10
15
?10
?15
?20
?25
20
?30
15
-25
20
-35
东
西
你可以列算式解决这个问题吗?
思考2:
和方向有关
和方向无关
解:(+15)+(-25)+(+20)+(-35)
=(15+20)+[(-25)+(-35)]
=35+(-60)
=-25(m)
|+15|+|-25|+|+20|+|-35|
=15+25+20+35
=95(m)
答:玩具赛车最后停在点A西面25m处,一共行驶了95m.
课堂练习
3.出租车司机小张某天的营运全是在东西走向的大道上进行的,规定向东为正,向西为负,他这天的行程(单位:km)是:+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距离出发点多少千米?在出发点的什么方向?
(2)已知汽车耗油量为0.6
L/km,出发时,油箱有油72.2
L.若小张将最后一名乘客送达目的地,再返回出发点.问:小张返回时是否需要加油?若要加油,至少要加多少油才能返回出发点?若不用加油,请说明理由.
(1)(+15)+(-3)+(+16)+(-11)+(+10)+(-12)+(+4)+(-15)+(+16)+(-18)
=2(km)
答:小张距离出发点2
km,在出发点的东面.
(2)|+15|+|-3|+|+16|+|-11|+|+10|+|-12|+|+4|+|-15|+|+16|+|-18|
=122(km)
所需油量:
122×0.6=73.2(L)
>72.2(L)
∴需要加油
∴至少要加73.2-72.2=1(L)油才能返回出发点.
课堂总结
加法交换律:
加法结合律:
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
a+b=b+a
(a+b)+c=a+(b+c)
文字语言
符号语言
文字语言
符号语言
1.同号结合
2.凑整(十)
3.同分母结合
4.带号换位
合并技巧:
板书设计
加法交换律:
加法结合律:
a+b=b+a
(a+b)+c=a+(b+c)
1.同号结合
2.凑整(十)
3.同分母结合
4.带号换位
合并技巧:
2.1有理数的加法(2)
作业布置
1.作业本2
2.1有理数的加法(2)
2.自主练习
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
