第2章 简单事件的概率单元训练卷(含解析)
文档属性
| 名称 | 第2章 简单事件的概率单元训练卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 09:43:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2021年九年级上册第2章《简单事件的概率》单元训练卷
一.选择题
1.下列说法正确的是( )
A.可能性很小的事情是不可能发生的
B.可能性很大的事情是必然发生的
C.投掷一枚普通的正方体骰子,结果恰好是“3”是不可能发生的
D.投掷一枚普通的正方体骰子,掷得的数不是奇数便是偶数是必然发生的
2.如图,要使摸到卡片5和卡片6的可能性相等,应该增加一张卡片( )
A.
B.
C.
D.
3.掷一枚质地均匀的硬币,硬币落下后,会出现两种情况,正面向上、反面向上.若连续掷这枚硬币4次都是正面向上,则关于第5次抛掷结果,下面叙述正确的是( )
A.P(正面向上)>P(反面向上)
B.P(正面向上)<P(反面向上)
C.P(正面向上)=P(反面向上)
D.以上都不对
4.一个不透明的盒子中装有9个除颜色外大小质量等都相同的乒乓球,其中4个是黄球,2个是白球,3个红球,从该盒子中任意摸出一个球,摸到红球的概率是( )
A.
B.
C.
D.
5.在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球实验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )
A.2个
B.4个
C.18个
D.16个
6.黄豆在相同条件下发芽率试验,结果如表.下面3个推断:①当n=100时,黄豆发芽的频率是0.970,所以黄豆发芽概率为0.970;②根据表格数据,估计黄豆发芽的概率为0.95;③若n=6000时,估计黄豆发芽的粒数约为5700.其中正确的个数为( )
每批粒数n
30
60
100
500
1000
3000
5000
发芽的粒数m
28
58
97
479
957
2844
4752
发芽的频率
0.933
0.967
0.970
0.958
0.957
0.948
0.950
A.0个
B.1个
C.2个
D.3个
7.如图,若干位同学玩扔石子进筐游戏,图①、图②分别是两种站立方式,关于这两种方式的“公平性”有下列说法,其中正确的是( )
A.两种均公平
B.两种均不公平
C.仅图①公平
D.仅图②公平
8.甲乙两人玩一个游戏,判定这个游戏公平不公平的标准是( )
A.游戏的规则由甲方确定
B.游戏的规则由乙方确定
C.游戏的规则由甲乙双方商定
D.游戏双方要各有50%赢的机会
9.某学习小组进行“用频率估计概率”的试验时,统计了某一结果出现的频率,并绘制了如图所示的折线统计图,则符合这一结果的试验可能是( )
A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上
B.先后两次掷一枚质地均匀的骰子,两次的点数和不大于3
C.小聪和小明玩剪刀、石头、布的游戏,小聪获胜
D.一个班级中班级人数为50人,有两人生日相同
10.这是一个古老的传说,讲一个犯人利用概率来增加他得到宽恕的机会.给他两个碗,一个里面装着5个黑球,另一个里面装着除颜色不同外其它都一样的5个白球.把他的眼睛蒙着,然后要选择一个碗,并从里面拿出一个球,如果他拿的是黑球就要继续关在监狱里面,如果他拿的是白球,就将获得自由.在蒙住眼睛之前允许他把球混合,重新分装在两个碗内(两个碗球数可以不同).你能设想一下这个犯人怎么做,使得自己获得自由的机会最大?则犯人获得自由的最大机会是( )
A.
B.
C.
D.
二.填空题
11.从,,0,﹣2,π,这五个数中随机抽取一个数,恰好是无理数的概率是
.
12.从﹣,﹣1,,2,5中任取一数作为a的值,能使抛物线y=ax2+bx+c的开口向下的概率为
.
13.在一个不透明的袋子里装有红球和白球共30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里白球可能是
个.
14.某商场庆“七一”建党节抽奖活动,顾客购物后就可通过转动转盘获得指针指向区域的奖项,顾客只有一次转动转盘的机会(指针与边缘线重合再来一次),其中二等奖对应的扇形圆心角为30°,则顾客获得二等奖的概率为
.
15.小明参加了一个抽奖游戏:一个不透明的布袋里装有1个红球,2个蓝球,4个黄球,8个白球,这些小球除颜色外完全相同.从布袋里摸出1球,摸到红球、蓝球、黄球、白球可分别得到奖金30元、20元、5元和0元,则小明摸一次球得到的平均收益是
元.
16.从不等式组的所有整数解中任取一个数,它是偶数的概率是
.
三.解答题
17.甲袋中有红球8个、白球5个和黑球12个;乙袋中有红球27个、白球35个和黑球16个.
(1)如果你想取出1个黑球,选哪个袋子成功的机会大?请说明理由;
(2)如果你想取出1个红球,选哪个袋子成功的机会大?请说明理由;
(3)“从乙袋中取出红球10个后,乙袋中的红球个数仍比甲袋中红球个数多,所以此时若想取出1个红球,选乙袋成功的机会大”.你认为此说法正确吗?为什么?
18.在一个不透明的布袋中,有六个完全相同的小球,把他们分别标号为1,2,2,3,4,5李强从布袋中随机摸出一个小球.
(1)求他摸出的小球标号是2的概率;
(2)求他摸出的小球标号小于4的概率;
(3)求他摸出的小球标号为偶数的概率.
19.口袋里有除颜色外都相同的4个球,其中有红球、白球和蓝球.甲乙两名同学玩摸球游戏.规定:无论谁从口袋里随意摸出一个球,摸到红球,算甲赢;摸到白球,算乙赢;摸到蓝球,不分输赢.每一次摸球,根据球的颜色决定输赢后,将球放回口袋里搅匀后下次再摸球.
设计下列游戏:
(1)要使甲、乙两人赢的可能性相等,口袋里应放红球、白球和蓝球各多少个?
(2)要使甲赢的可能性比乙赢的可能性大,口袋里应放红球、白球和蓝球各多少个?
20.如图,现有一个均匀的转盘被平均分成8等份,分别标有2、4、6、8、10、12、14、16这8个数字.转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,无效,重转).
(1)转动转盘,转出的数字是4的倍数的概率是多少;
(2)小明和小红进行游戏:各自转相同的次数,指针指向3的倍数则小明胜,指针指向4的倍数则小红胜,这个游戏公平吗?为什么?如果让你根据这个转盘来设计一个公平的游戏,你会怎么设计呢?
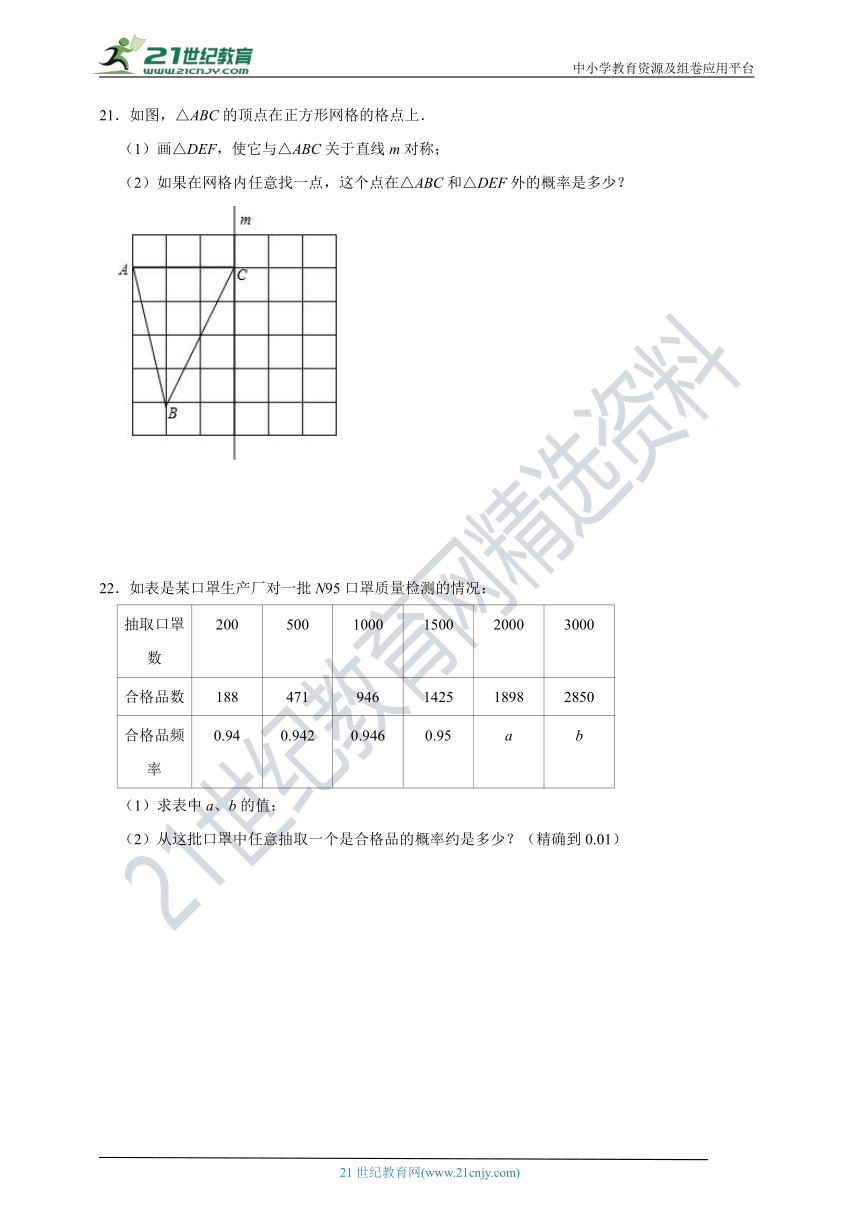
21.如图,△ABC的顶点在正方形网格的格点上.
(1)画△DEF,使它与△ABC关于直线m对称;
(2)如果在网格内任意找一点,这个点在△ABC和△DEF外的概率是多少?
22.如表是某口罩生产厂对一批N95口罩质量检测的情况:
抽取口罩数
200
500
1000
1500
2000
3000
合格品数
188
471
946
1425
1898
2850
合格品频率
0.94
0.942
0.946
0.95
a
b
(1)求表中a、b的值;
(2)从这批口罩中任意抽取一个是合格品的概率约是多少?(精确到0.01)
23.今年在2月27日国务院对外新闻发布会上,中国疾控中心发言人提到:“在新冠肺炎低风险区域出行仍需戴口罩.”某单位复工,采购了一批医用外科口罩,单价分别为1元、1.5元、3元、5元、10元,每天随机配发给每位在岗员工一个口罩.现将连续10天口罩配发量的情况制成如统计表.
配发量/个
30
25
20
15
天数/天
2
x
y
1
已知配发量的平均数是23个,中位数是m个,众数是n个.
(1)求x,y的值,并计算m﹣n;
(2)将配发15个口罩那一天中不同型号的口罩发放情况进行统计,绘制成如图所示的尚不完整的统计图.补全统计图,并求小李当天获得不低于3元口罩的概率;
(3)若继续发放两天口罩,且这12天口罩配发量的众数与前10天口罩配发量的众数不同(例如:只要在第11天,第12天都发放30个口罩,则这12天口罩发放量的众数为30个和20个),写出这12天口罩配发量的众数(括号内示例情况不必再述).
参考答案
一.选择题
1.【解答】解:A、可能性很小的事情是可能发生的,本选项说法错误;
B、可能性很大的事情不一定是必然发生的,本选项说法错误;
C、投掷一枚普通的正方体骰子,结果恰好是“3”是随机事件,本选项说法错误;
D、投掷一枚普通的正方体骰子,掷得的数不是奇数便是偶数是必然发生的,故本选项说法正确;
故选:D.
2.【解答】解:要使摸到卡片5和卡片6的可能性相等,则卡片5和卡片6的张数相等,
所以应该增加一张卡片6,
故选:B.
3.【解答】解:∵抛掷一枚质地均匀的硬币一次,可能的结果有:正面向上,反面向上;
∴P(正面向上)=P(反面向上)=.
故选:C.
4.【解答】解:∵一个不透明的盒子中装有6个除颜色外其他均相同的乒乓球,其中4个是黄球,2个是白球3个红球,
∴从该盒子中任意摸出一个球,摸到红球的概率是:=.
故选:A.
5.【解答】解:设袋中有黄球x个,由题意得=0.2,
解得x=16.
故选:D.
6.【解答】解:①当n=100时,黄豆发芽的频率是0.970,所以黄豆发芽概率为0.970;此推断错误;
②根据表格数据,估计黄豆发芽的概率为0.95;此推断正确;
③若n=6000时,估计黄豆发芽的粒数约为6000×0.95=5700.此结论正确.
故选:C.
7.【解答】解:图①中,若干位同学到筐的距离不相等,则图①不公平;
图②中,若干位同学到筐的距离相等,则图②公平;
故选:D.
8.【解答】解:根据游戏是否公平不在于谁定游戏规则,游戏是否公平的取决于游戏双方要各有50%赢的机会,
∴A.游戏的规则由甲方确定,胜负机会不一定不均等,故此选项错误;
B.游戏的规则由乙方确定,胜负机会不一定不均等,故此选项错误;
C.游戏的规则由甲乙双方商定,胜负机会不一定不均等,故此选项错误;
D.游戏双方要各有50%赢的机会,胜负机会均等,故此选项正确.
故选:D.
9.【解答】解:A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上的概率为,与图形不符,不符合题意;
B.先后两次掷一枚质地均匀的骰子,两次的点数和不大于3的概率为=,与图形不符,不符合题意;
C.小聪和小明玩剪刀、石头、布的游戏,小聪获胜的概率为=,与图形相符,符合题意;
D.一个班级中班级人数为50人,有两人生日相同的概率为×≈0,与图形不符,不符合题意;
故选:C.
10.【解答】解:可以先将所有的球放入一个碗,再拿出一个白球放在另一个碗里.这样,他若选择只有一个白球的碗获得自由的概率1,如果他选择错了碗,从另一个碗里摸到白球的概率是,从而所以获得自由的概率最大是.
故选:D.
二.填空题
11.【解答】解:从,,0,﹣2,π这五个数中随机抽取一个数,抽到的无理数的有,π这2种可能,
∴抽到的无理数的概率是,
故答案为:.
12.【解答】解:在所列的5个数中任取一个数有5种等可能结果,其中使抛物线y=ax2+bx+c的开口向上的有,2,5共3种结果,
∴使抛物线y=ax2+bx+c的开口向上的概率为,
故答案为:.
13.【解答】解:由题意可得,
30×0.3=9(个),
即袋子中白球的个数最有可能是9个,
故答案为:9.
14.【解答】解:∵整个圆的圆周角是360°,其中标有二等奖区域的圆周角是30°,
∴顾客获得二等奖的概率为=.
故答案为:.
15.【解答】解:∵一个不透明的布袋里装有1个红球,2个蓝球,4个黄球,8个白球,这些小球除颜色外完全相同,
∴一共有球1+2+4+8=15(个),
∴从布袋里摸出1球,摸到红球、蓝球、黄球、白球的概率分别是:,,,,
又摸到红球、蓝球、黄球、白球可分别得到奖金30元、20元、5元和0元,
∴小明摸一次球得到的平均收益是:30×+20×+5×+0×=2++=6(元).
故答案为:6.
16.【解答】解:∵,
由①得:x≥1,
由②得:x≤5,
∴不等式组的解集为:1≤x≤5,
∴整数解有:1,2,3,4,5;
∴它是偶数的概率是.
故答案为.
三.解答题
17.【解答】解:(1)选甲袋子成功的机会大.
理由如下:
在甲袋中取出1个黑球的概率==,在乙袋中取出1个黑球的概率==,
因为>,
所以选甲袋子成功的机会大;
(2)选乙袋子成功的机会大.
理由如下:
在甲袋中取出1个红球的概率==,在乙袋中取出1个红球的概率==,
因为>,
所以选乙袋子成功的机会大;
(3)这个说法不正确.
因为从乙袋中取出红球10个后,从乙袋中取出1个红球的概率==,
而>,
所以此时若想取出1个红球,选甲袋成功的机会大.
18.【解答】解:(1)∵共6个球,标号为2的有2个,
∴摸出的小球标号是2的概率是=;
(2)∵共6个小球,标号小于4的有4个,
∴摸出的小球标号小于4的概率为=;
(3)∵共6个球,为偶数的有3个,
∴摸出的小球为偶数的概率为=.
19.【解答】解:(1)要使甲、乙两人赢的可能性相等,口袋里应放红球1个,白球1个,蓝球2个;
(2)要使甲赢的可能性比乙赢的可能性大,口袋里应放红球2个,白球1个,蓝球1个.
20.【解答】解:(1)转动转盘,转出的数字是4的倍数的概率==;
(2)这个游戏不公平.
理由如下:转动一次,指针指向3的倍数的结果数为2,所以小明胜的概率==,
指针指向4的倍数的结果数为4,所以小红胜的概率==,
而>,
所以这个游戏不公平.
设计一个公平的游戏可为:各自转相同的次数,指针指向不是4的倍数则小明胜,指针指向是4的倍数则小红胜.
21.【解答】解:(1)如图所示:
(2)网格的面积为6×6=36,
△ABC和△DEF外的面积为36﹣3×4÷2×2=24,
故这个点在△ABC和△DEF外的概率是=.
22.【解答】解:(1)1898÷2000=0.949,2850÷3000=0.950;
(2)由表格可知,随着抽取的口罩数量不断增大,任意抽取一个是合格的频率在0.95附近波动,
所以任意抽取的一个是合格品的概率估计值是0.95;
23.【解答】解:(1)∵平均数为23个,
∴,
解得,
将10个数据按从大到小的顺序排列,第5、6个数据分别是25,20,
所以中位数m==22.5,
数据20出现了4次,次数最多,所以众数n=20.
∴m﹣n=2.5.
(2)补全统计图如图所示:
在这5种型号中,单价不低于3元的有3元、5元、10元三种,
∴小李当天获得不低于3元的口罩的概率为:.
(3)由表格可知:
配发量/个
30
25
20
15
天数/天
2
3
4
1
因为这12天口罩配发量的众数发生改变,除示例情况外还有两种情况:
情况一:两天都配发25个,众数变为25个;
情况二:其中一天配发25个,另一天配发30个或15个,众数变为25个和20个.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版2021年九年级上册第2章《简单事件的概率》单元训练卷
一.选择题
1.下列说法正确的是( )
A.可能性很小的事情是不可能发生的
B.可能性很大的事情是必然发生的
C.投掷一枚普通的正方体骰子,结果恰好是“3”是不可能发生的
D.投掷一枚普通的正方体骰子,掷得的数不是奇数便是偶数是必然发生的
2.如图,要使摸到卡片5和卡片6的可能性相等,应该增加一张卡片( )
A.
B.
C.
D.
3.掷一枚质地均匀的硬币,硬币落下后,会出现两种情况,正面向上、反面向上.若连续掷这枚硬币4次都是正面向上,则关于第5次抛掷结果,下面叙述正确的是( )
A.P(正面向上)>P(反面向上)
B.P(正面向上)<P(反面向上)
C.P(正面向上)=P(反面向上)
D.以上都不对
4.一个不透明的盒子中装有9个除颜色外大小质量等都相同的乒乓球,其中4个是黄球,2个是白球,3个红球,从该盒子中任意摸出一个球,摸到红球的概率是( )
A.
B.
C.
D.
5.在一个不透明的盒子中装有20个黄、白两种颜色的乒乓球,除颜色外其它都相同,小明进行了多次摸球实验,发现摸到白色乒乓球的频率稳定在0.2左右,由此可知盒子中黄色乒乓球的个数可能是( )
A.2个
B.4个
C.18个
D.16个
6.黄豆在相同条件下发芽率试验,结果如表.下面3个推断:①当n=100时,黄豆发芽的频率是0.970,所以黄豆发芽概率为0.970;②根据表格数据,估计黄豆发芽的概率为0.95;③若n=6000时,估计黄豆发芽的粒数约为5700.其中正确的个数为( )
每批粒数n
30
60
100
500
1000
3000
5000
发芽的粒数m
28
58
97
479
957
2844
4752
发芽的频率
0.933
0.967
0.970
0.958
0.957
0.948
0.950
A.0个
B.1个
C.2个
D.3个
7.如图,若干位同学玩扔石子进筐游戏,图①、图②分别是两种站立方式,关于这两种方式的“公平性”有下列说法,其中正确的是( )
A.两种均公平
B.两种均不公平
C.仅图①公平
D.仅图②公平
8.甲乙两人玩一个游戏,判定这个游戏公平不公平的标准是( )
A.游戏的规则由甲方确定
B.游戏的规则由乙方确定
C.游戏的规则由甲乙双方商定
D.游戏双方要各有50%赢的机会
9.某学习小组进行“用频率估计概率”的试验时,统计了某一结果出现的频率,并绘制了如图所示的折线统计图,则符合这一结果的试验可能是( )
A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上
B.先后两次掷一枚质地均匀的骰子,两次的点数和不大于3
C.小聪和小明玩剪刀、石头、布的游戏,小聪获胜
D.一个班级中班级人数为50人,有两人生日相同
10.这是一个古老的传说,讲一个犯人利用概率来增加他得到宽恕的机会.给他两个碗,一个里面装着5个黑球,另一个里面装着除颜色不同外其它都一样的5个白球.把他的眼睛蒙着,然后要选择一个碗,并从里面拿出一个球,如果他拿的是黑球就要继续关在监狱里面,如果他拿的是白球,就将获得自由.在蒙住眼睛之前允许他把球混合,重新分装在两个碗内(两个碗球数可以不同).你能设想一下这个犯人怎么做,使得自己获得自由的机会最大?则犯人获得自由的最大机会是( )
A.
B.
C.
D.
二.填空题
11.从,,0,﹣2,π,这五个数中随机抽取一个数,恰好是无理数的概率是
.
12.从﹣,﹣1,,2,5中任取一数作为a的值,能使抛物线y=ax2+bx+c的开口向下的概率为
.
13.在一个不透明的袋子里装有红球和白球共30个,这些球除颜色外都相同,小明通过多次试验发现,摸出白球的频率稳定在0.3左右,则袋子里白球可能是
个.
14.某商场庆“七一”建党节抽奖活动,顾客购物后就可通过转动转盘获得指针指向区域的奖项,顾客只有一次转动转盘的机会(指针与边缘线重合再来一次),其中二等奖对应的扇形圆心角为30°,则顾客获得二等奖的概率为
.
15.小明参加了一个抽奖游戏:一个不透明的布袋里装有1个红球,2个蓝球,4个黄球,8个白球,这些小球除颜色外完全相同.从布袋里摸出1球,摸到红球、蓝球、黄球、白球可分别得到奖金30元、20元、5元和0元,则小明摸一次球得到的平均收益是
元.
16.从不等式组的所有整数解中任取一个数,它是偶数的概率是
.
三.解答题
17.甲袋中有红球8个、白球5个和黑球12个;乙袋中有红球27个、白球35个和黑球16个.
(1)如果你想取出1个黑球,选哪个袋子成功的机会大?请说明理由;
(2)如果你想取出1个红球,选哪个袋子成功的机会大?请说明理由;
(3)“从乙袋中取出红球10个后,乙袋中的红球个数仍比甲袋中红球个数多,所以此时若想取出1个红球,选乙袋成功的机会大”.你认为此说法正确吗?为什么?
18.在一个不透明的布袋中,有六个完全相同的小球,把他们分别标号为1,2,2,3,4,5李强从布袋中随机摸出一个小球.
(1)求他摸出的小球标号是2的概率;
(2)求他摸出的小球标号小于4的概率;
(3)求他摸出的小球标号为偶数的概率.
19.口袋里有除颜色外都相同的4个球,其中有红球、白球和蓝球.甲乙两名同学玩摸球游戏.规定:无论谁从口袋里随意摸出一个球,摸到红球,算甲赢;摸到白球,算乙赢;摸到蓝球,不分输赢.每一次摸球,根据球的颜色决定输赢后,将球放回口袋里搅匀后下次再摸球.
设计下列游戏:
(1)要使甲、乙两人赢的可能性相等,口袋里应放红球、白球和蓝球各多少个?
(2)要使甲赢的可能性比乙赢的可能性大,口袋里应放红球、白球和蓝球各多少个?
20.如图,现有一个均匀的转盘被平均分成8等份,分别标有2、4、6、8、10、12、14、16这8个数字.转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时,无效,重转).
(1)转动转盘,转出的数字是4的倍数的概率是多少;
(2)小明和小红进行游戏:各自转相同的次数,指针指向3的倍数则小明胜,指针指向4的倍数则小红胜,这个游戏公平吗?为什么?如果让你根据这个转盘来设计一个公平的游戏,你会怎么设计呢?
21.如图,△ABC的顶点在正方形网格的格点上.
(1)画△DEF,使它与△ABC关于直线m对称;
(2)如果在网格内任意找一点,这个点在△ABC和△DEF外的概率是多少?
22.如表是某口罩生产厂对一批N95口罩质量检测的情况:
抽取口罩数
200
500
1000
1500
2000
3000
合格品数
188
471
946
1425
1898
2850
合格品频率
0.94
0.942
0.946
0.95
a
b
(1)求表中a、b的值;
(2)从这批口罩中任意抽取一个是合格品的概率约是多少?(精确到0.01)
23.今年在2月27日国务院对外新闻发布会上,中国疾控中心发言人提到:“在新冠肺炎低风险区域出行仍需戴口罩.”某单位复工,采购了一批医用外科口罩,单价分别为1元、1.5元、3元、5元、10元,每天随机配发给每位在岗员工一个口罩.现将连续10天口罩配发量的情况制成如统计表.
配发量/个
30
25
20
15
天数/天
2
x
y
1
已知配发量的平均数是23个,中位数是m个,众数是n个.
(1)求x,y的值,并计算m﹣n;
(2)将配发15个口罩那一天中不同型号的口罩发放情况进行统计,绘制成如图所示的尚不完整的统计图.补全统计图,并求小李当天获得不低于3元口罩的概率;
(3)若继续发放两天口罩,且这12天口罩配发量的众数与前10天口罩配发量的众数不同(例如:只要在第11天,第12天都发放30个口罩,则这12天口罩发放量的众数为30个和20个),写出这12天口罩配发量的众数(括号内示例情况不必再述).
参考答案
一.选择题
1.【解答】解:A、可能性很小的事情是可能发生的,本选项说法错误;
B、可能性很大的事情不一定是必然发生的,本选项说法错误;
C、投掷一枚普通的正方体骰子,结果恰好是“3”是随机事件,本选项说法错误;
D、投掷一枚普通的正方体骰子,掷得的数不是奇数便是偶数是必然发生的,故本选项说法正确;
故选:D.
2.【解答】解:要使摸到卡片5和卡片6的可能性相等,则卡片5和卡片6的张数相等,
所以应该增加一张卡片6,
故选:B.
3.【解答】解:∵抛掷一枚质地均匀的硬币一次,可能的结果有:正面向上,反面向上;
∴P(正面向上)=P(反面向上)=.
故选:C.
4.【解答】解:∵一个不透明的盒子中装有6个除颜色外其他均相同的乒乓球,其中4个是黄球,2个是白球3个红球,
∴从该盒子中任意摸出一个球,摸到红球的概率是:=.
故选:A.
5.【解答】解:设袋中有黄球x个,由题意得=0.2,
解得x=16.
故选:D.
6.【解答】解:①当n=100时,黄豆发芽的频率是0.970,所以黄豆发芽概率为0.970;此推断错误;
②根据表格数据,估计黄豆发芽的概率为0.95;此推断正确;
③若n=6000时,估计黄豆发芽的粒数约为6000×0.95=5700.此结论正确.
故选:C.
7.【解答】解:图①中,若干位同学到筐的距离不相等,则图①不公平;
图②中,若干位同学到筐的距离相等,则图②公平;
故选:D.
8.【解答】解:根据游戏是否公平不在于谁定游戏规则,游戏是否公平的取决于游戏双方要各有50%赢的机会,
∴A.游戏的规则由甲方确定,胜负机会不一定不均等,故此选项错误;
B.游戏的规则由乙方确定,胜负机会不一定不均等,故此选项错误;
C.游戏的规则由甲乙双方商定,胜负机会不一定不均等,故此选项错误;
D.游戏双方要各有50%赢的机会,胜负机会均等,故此选项正确.
故选:D.
9.【解答】解:A.先后两次抛掷一枚质地均匀的硬币,两次都是反面朝上的概率为,与图形不符,不符合题意;
B.先后两次掷一枚质地均匀的骰子,两次的点数和不大于3的概率为=,与图形不符,不符合题意;
C.小聪和小明玩剪刀、石头、布的游戏,小聪获胜的概率为=,与图形相符,符合题意;
D.一个班级中班级人数为50人,有两人生日相同的概率为×≈0,与图形不符,不符合题意;
故选:C.
10.【解答】解:可以先将所有的球放入一个碗,再拿出一个白球放在另一个碗里.这样,他若选择只有一个白球的碗获得自由的概率1,如果他选择错了碗,从另一个碗里摸到白球的概率是,从而所以获得自由的概率最大是.
故选:D.
二.填空题
11.【解答】解:从,,0,﹣2,π这五个数中随机抽取一个数,抽到的无理数的有,π这2种可能,
∴抽到的无理数的概率是,
故答案为:.
12.【解答】解:在所列的5个数中任取一个数有5种等可能结果,其中使抛物线y=ax2+bx+c的开口向上的有,2,5共3种结果,
∴使抛物线y=ax2+bx+c的开口向上的概率为,
故答案为:.
13.【解答】解:由题意可得,
30×0.3=9(个),
即袋子中白球的个数最有可能是9个,
故答案为:9.
14.【解答】解:∵整个圆的圆周角是360°,其中标有二等奖区域的圆周角是30°,
∴顾客获得二等奖的概率为=.
故答案为:.
15.【解答】解:∵一个不透明的布袋里装有1个红球,2个蓝球,4个黄球,8个白球,这些小球除颜色外完全相同,
∴一共有球1+2+4+8=15(个),
∴从布袋里摸出1球,摸到红球、蓝球、黄球、白球的概率分别是:,,,,
又摸到红球、蓝球、黄球、白球可分别得到奖金30元、20元、5元和0元,
∴小明摸一次球得到的平均收益是:30×+20×+5×+0×=2++=6(元).
故答案为:6.
16.【解答】解:∵,
由①得:x≥1,
由②得:x≤5,
∴不等式组的解集为:1≤x≤5,
∴整数解有:1,2,3,4,5;
∴它是偶数的概率是.
故答案为.
三.解答题
17.【解答】解:(1)选甲袋子成功的机会大.
理由如下:
在甲袋中取出1个黑球的概率==,在乙袋中取出1个黑球的概率==,
因为>,
所以选甲袋子成功的机会大;
(2)选乙袋子成功的机会大.
理由如下:
在甲袋中取出1个红球的概率==,在乙袋中取出1个红球的概率==,
因为>,
所以选乙袋子成功的机会大;
(3)这个说法不正确.
因为从乙袋中取出红球10个后,从乙袋中取出1个红球的概率==,
而>,
所以此时若想取出1个红球,选甲袋成功的机会大.
18.【解答】解:(1)∵共6个球,标号为2的有2个,
∴摸出的小球标号是2的概率是=;
(2)∵共6个小球,标号小于4的有4个,
∴摸出的小球标号小于4的概率为=;
(3)∵共6个球,为偶数的有3个,
∴摸出的小球为偶数的概率为=.
19.【解答】解:(1)要使甲、乙两人赢的可能性相等,口袋里应放红球1个,白球1个,蓝球2个;
(2)要使甲赢的可能性比乙赢的可能性大,口袋里应放红球2个,白球1个,蓝球1个.
20.【解答】解:(1)转动转盘,转出的数字是4的倍数的概率==;
(2)这个游戏不公平.
理由如下:转动一次,指针指向3的倍数的结果数为2,所以小明胜的概率==,
指针指向4的倍数的结果数为4,所以小红胜的概率==,
而>,
所以这个游戏不公平.
设计一个公平的游戏可为:各自转相同的次数,指针指向不是4的倍数则小明胜,指针指向是4的倍数则小红胜.
21.【解答】解:(1)如图所示:
(2)网格的面积为6×6=36,
△ABC和△DEF外的面积为36﹣3×4÷2×2=24,
故这个点在△ABC和△DEF外的概率是=.
22.【解答】解:(1)1898÷2000=0.949,2850÷3000=0.950;
(2)由表格可知,随着抽取的口罩数量不断增大,任意抽取一个是合格的频率在0.95附近波动,
所以任意抽取的一个是合格品的概率估计值是0.95;
23.【解答】解:(1)∵平均数为23个,
∴,
解得,
将10个数据按从大到小的顺序排列,第5、6个数据分别是25,20,
所以中位数m==22.5,
数据20出现了4次,次数最多,所以众数n=20.
∴m﹣n=2.5.
(2)补全统计图如图所示:
在这5种型号中,单价不低于3元的有3元、5元、10元三种,
∴小李当天获得不低于3元的口罩的概率为:.
(3)由表格可知:
配发量/个
30
25
20
15
天数/天
2
3
4
1
因为这12天口罩配发量的众数发生改变,除示例情况外还有两种情况:
情况一:两天都配发25个,众数变为25个;
情况二:其中一天配发25个,另一天配发30个或15个,众数变为25个和20个.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
