第2章 简单事件的概率单元综合测试卷(含解析)
文档属性
| 名称 | 第2章 简单事件的概率单元综合测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 509.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-05 09:46:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2021年九年级上册第2章《简单事件的概率》单元综合测试卷
(满分100分)
一、选择题(共10题;共30分)
1.下列语句描述的事件中,是随机事件的为(??
)
A.?水能载舟,亦能覆舟???????????????????????????????????????????B.?只手遮天,偷天换日
C.?瓜熟蒂落,水到渠成???????????????????????????????????????????D.?心想事成,万事如意
2.一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是必然事件的为(??
)
A.?至少有1个球是黑球??????B.?至少有1个球是白球??????C.?至少有2个球是黑球??????D.?至少有2个球是白球
3.“14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则(??
)
A.?P=0??????????????????????????????????B.?0<P<1??????????????????????????????????C.?P=1??????????????????????????????????D.?P>1
4.王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A.?16人?????????????????????????????????????B.?14人?????????????????????????????????????C.?4人?????????????????????????????????????D.?6人
5.从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是(??
)
A.?0???????????????????????????????????????????B.????????????????????????????????????????????C.????????????????????????????????????????????D.?1
6.随机掷一枚质地均匀的硬币两次,落地后至多有一次正面朝下的概率为(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
7.如图,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路,则使电路形成通路的概率是(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
8.甲乙两人轮流在黑板上写下不超过
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字(
??)时有必胜的策略.
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
9.如果
是随机投掷一枚骰子所得的数字(1,2,3,4,5,6),则关于
的一元二次方程
有两个不等实数根的概率P=
(????
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
10.“五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”区域的次数m
68
108
140
355
560
690
落在“铅笔”区域的频率
0.68
0.72
0.70
0.71
0.70
0.69
下列说法不正确的是(???
)
A.?当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70
B.?假如你去转动转盘一次,获得“铅笔”概率大约是0.70
C.?如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次
D.?转动转盘20次,一定有6次获得“文具盒”
二、填空题(共6题;共18分)
11.“同位角相等”,这是________事件(选填“随机”或“必然”).
12.在-1,0,
,
,π,0.10110中任取一个数,取到无理数的概率是________.
13.从
1,2,3,4,5,6,7,8,9,10这十个数中随机取出一个数,取出的数是3的倍数的概率是________.
14.如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是________
.
15.有五张背面完全相同的卡片,其正面分别画有等腰三角形、平行四边形、矩形、正方形、菱形,将这五张卡片背面朝上洗匀,从中随机抽取一张,卡片上的图形是中心对称图形的概率是________.
16.动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此若设刚出生的这种动物共有a只.则20年后存活的有________只,现年20岁的这种动物活到25岁的概率是________.
三、解答题(共6题;共52分)
17.有两个可以自由转动的均匀转盘
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).
用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
18.布袋里有四个小球,球表面分别标有2、3、4、6四个数字,它们的材质、形状、大小完全相同。从中随机摸出一个小球记下数字为x,再从剩下的三个球中随机摸出一个球记下数字为y,点A的坐标为(x,y).运用画树状图或列表的方法,写出A点所有可能的坐标,并求出点A在反比例函数
图象上的概率.
19.小明、小林是某中学九年级的同班同学.在三月份举行的自主招生考试中,他俩都被同一所高中提前录取,并被编入A,B,C三个班,他俩希望能两次成为同班同学.
(1)请你用画树状图法或列举法,列出所有可能的结果;
(2)求两人两次成为同班同学的概率.
20.在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,李晓同学从布袋里随机取出一个小球,记下数字为x,张丹同学在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+6图象上的概率.
21.已知不等式组
?
(1)求不等式组的解,并写出它的所有整数解.??
(2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
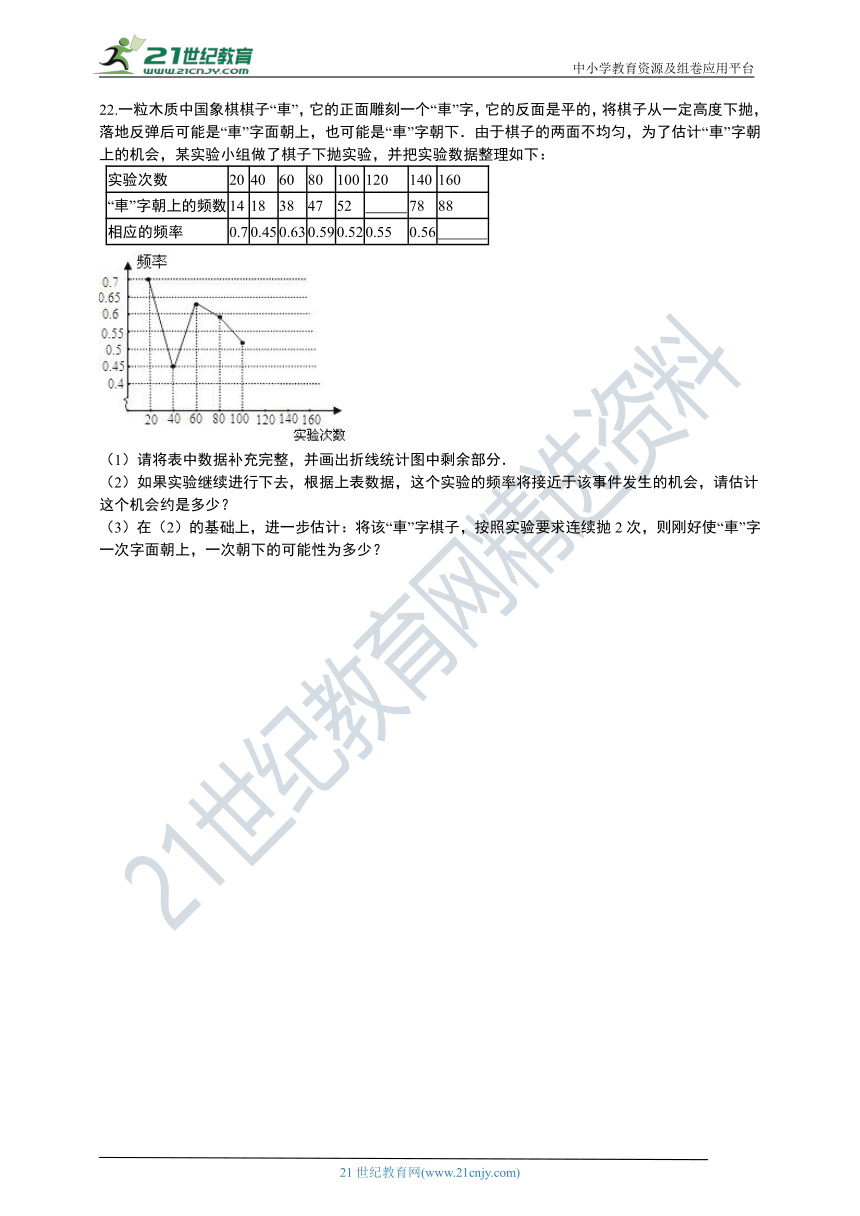
22.一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52
??
?
?
?
78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56
?
?
?
?
?
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
(3)在(2)的基础上,进一步估计:将该“車”字棋子,按照实验要求连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为多少?
参考答案
一、选择题
1.【答案】
D
【解析】【解答】解:A、水能载舟,亦能覆舟,是必然事件,故不符合题意;
B、只手遮天,偷天换日,是不可能事件,故不符合题意;
C、瓜熟蒂落,水到渠成,是必然事件,故不符合题意;
D、心想事成,万事如意,是随机事件,故符合题意.
故答案为:D.
所谓随机事件,就是可能发生,也可能不会发生的事件,根据概念即可一一判断。
2.【答案】
A
【解析】【解答】至少有1个球是黑球是必然事件,A正确;至少有1个球是白球是随机事件,B不正确;至少有2个球是黑球是随机事件,C不正确;至少有2个球是白球是随机事件,D不正确;故答案为:A.
随机事件是在一定条件下,可能发生也可能不发生的事件;必然事件是在一定条件下,一定发生的事件;不可能事件是在一定条件下,一定不发生的事件;据此判断即可.
3.【答案】
C
【解析】【解答】解:∵一年有12个月,14个人中有12个人在不同的月份过生日,剩下的两人不论哪个月生日,都和前12人中的一个人同一个月过生日
∴“14人中至少有2人在同一个月过生日”是必然事件,
即这一事件发生的概率为
.
故答案为:C.
先确定“14人中至少有2人在同一个月过生日”这一事件为必然事件,从而求出结论.
4.【答案】
A
【解析】【解答】本班A型血的人数为:40×0.4=16.
故选:A.
根据频数和频率的定义求解即可.
5.【答案】
B
【解析】【解答】解:
共有6种情况,积是正数的有2种情况,故概率为
,
故选:B.
列举出所有情况,看积是正数的情况数占总情况数的多少即可.
6.【答案】
A
【解析】【解答】随机掷一枚质地均匀的硬币两次,共“正、反”,“反、正”,“正、正”,“反、反”,4种情况,落地后至多有一次正面朝下包括“正、反”,“反、正”,“正、正”,3种情况,
故至多有一次正面朝下的概率为
.
故答案为:A.
用列举法确定所有等可能的情况,根据落地后至多有一次正面朝下的次数,利用概率公式计算解答.
7.【答案】
C
【解析】【解答】共有5个开关,任意闭合2个,共有5×4÷2=10种情况;在闭合a的情况下,有3种情况出现通路,同理,在闭合b的情况下,也出现3种通路.共有6种通路.∴使电路形成通路的概率是
,
故答案为:C.
找出闭合a,b,c,d,e五个开关中的任意两个开关的所有情况,
再作出只有闭合两条线路里的两个才能形成通路的所有情况,代入概率的计算公式即可求出使电路形成通路的概率
.
8.【答案】
D
【解析】【解答】对于选项A:当甲写10时,乙可以写3、4、6、7、8、9,如果乙写7,则乙必胜,因为无论甲写3,4,6,8,9这五个数中的6(连带3)或8(连带4),乙可以写4或3,剩下2个数字;当甲写3或4时,乙可以写8(连带4)或6(连带3),剩下偶数个数字甲最后不能写,乙必胜;
对于选项B:当甲写9后,乙可以写2、4、5、6、7、8、10,如果乙写6,则乙必胜,因为剩下4、5、7、8、10这5个数中,无论甲写8(连带4)或10(连带5),乙可以写5或4;当甲写4或5时,乙可以写10(连带5)或8(连带4),甲最后不能写,乙必胜;
对于选项C:当甲写8时,乙可以写3、5、6、7、9、10,当乙写6(或10)时,甲就必须写10(或6),因为乙写6(或10)后,连带3(或5)也不能写了,这样才能保证剩下能写的数有偶数个,甲才可以获胜;
对于选项D:
甲先写6,由于6的约数有1,2,3,6,接下来乙可以写的数只有4、5、7、8、9、10,把这6个数分成三组:(4,7)、(5,8)、(9,10),当然也可(4,5)、(8,10)、(7,9)或(4,9)、(5,7)、(8,10)等等,只要组内两数大数不是小数的倍数即可,这样,乙写某组数中的某个数时,甲就写同组中的另一数,从而甲一定写最后一个,甲必获胜,
综上可知,只有甲先写6,才能必胜,
故答案为:D.
根据游戏规则,分别将四个答案,一一分析,判断出最后一个能书写的是谁即可得出答案。
9.【答案】
A
【解析】【解答】∵一元二次方程
有两个不等实数根,
∴
?,
∴k<5且k≠1,
∵
是随机投掷一枚骰子所得的数字(1,2,3,4,5,6),共6种情况
∴能使关于
的一元二次方程
有两个不等实数根的k值为2、3、4,共计3种情况,
∴关于
的一元二次方程
有两个不等实数根的概率P=
=
,
故答案为:A.
根据一元二次方程的定义,二次项的系数不能为0,又此方程有两个不相等的实数根,故根的判别式应该大于0,从而列出不等式组,求解得出k的取值范围,随机投掷一枚骰子所得的数字(1,2,3,4,5,6),共6种情况,能使关于
x
的一元二次方程
(
k
?
1
)
x2
+
4
x
+
1
=
0
有两个不等实数根的k值为2、3、4,共计3种情况,故根据概率公式即可算出答案。
10.【答案】
D
【解析】【解答】A、频率稳定在0.7左右,故用频率估计概率,指针落在“铅笔”区域的频率大约是0.70,故A选项符合题意;
由A可知B、转动转盘一次,获得铅笔的概率大约是0.70,故B选项符合题意;
C、指针落在“文具盒”区域的概率为0.30,转动转盘2000次,指针落在“文具盒”区域的次数大约有3000×0.3=900次,故C选项符合题意;
D、随机事件,结果不确定,故D选项符合题意.
故答案为:D
.
根据图表可求得指针落在铅笔区域的概率,另外概率是多次实验的结果,因此不能说转动转盘20次,一定有6次获得文具盒.
二、填空题
11.【答案】
随机
【解析】【解答】“同位角相等”,这是随机事件.
故答案为:随机.
同位角只有在二直线平行的情况下才相等,如果二直线不平行,则同位角是不相等的,故事随机事件。
12.【答案】
【解析】【解答】共有6个实数,其中无理数有2个,所以取到无理数的概率是
.
故本题应填
.
在这些数中,随机的取出一个数,共有6种等可能的结果,其中能取出无理数的只有两种等可能结果,根据概率公式即可算出取到无理数的概率。
13.【答案】
【解析】【解答】∵1、2、3、4、5、6、7、8、9、10这十个数中,3的倍数的有3、6、9共3个数,
∴取出的数是3的倍数的概率是:
.
故答案为:
从1、2、3、4、5、6、7、8、9、10这十个数中随机的取出一个数字,共有10种等可能的结果,其中是3的倍数的有3、6、9共3种情况,根据概率公式即可算出取出的数是3的倍数的概率。
14.【答案】
【解析】【解答】画树状图得:
∵共有6种等可能的结果,转盘所转到的两个数字之积为奇数的有2种情况,
∴转盘所转到的两个数字之积为奇数的概率是:
.
故答案是:
转动第一个转盘共有两种等可能的结果,转动第二个转盘共有三种等可能的结果,根据题意,画出树状图,由图知:共有6种等可能的结果,转盘所转到的两个数字之积为奇数的有2种情况,根据概率公式即可求出转盘所转到的两个数字之积为奇数的概率。
15.【答案】
【解析】【解答】解:∵等腰三角形、平行四边形、矩形、正方形、菱形中,平行四边形、矩形、正方形、菱形都是中心对称图形,
∴从中随机抽取一张,卡片上的图形是中心对称图形的概率是:
.
故答案为:
.
有五张背面完全相同的卡片,其正面分别画有等腰三角形、平行四边形、矩形、正方形、菱形,将这五张卡片背面朝上洗匀,从中随机抽取一张共有5种等可能的结果,其中是中心对称图形的只有4种,根据概率公式即可得出答案。
16.【答案】
;
【解析】【解答】解:共有a只这种动物
∵这种动物活到20岁的概率为0.8,活到25岁的概率为0.5,
∴这种动物活到20岁的有0.8a只,活到25岁的有0.5a只,
∴现年20岁的这种动物活到25岁的概率是0.5a÷0.8a=
故答案为:
.
先求出这种动物活到20岁的有0.8a只,活到25岁的有0.5a只,再求概率即可。
三、解答题
17.【答案】
解:P(3的倍数)=
P(5的倍数)=
【解析】根据题意,转动转盘A共有3种等可能的结果,转动转盘B也共有3种等可能的结果,根据题意画出树状图,由图知:共有9种等可能的结果,其中两次转动,指针所指的两个数字之积是3的倍数的共有5种,两次转动,指针所指的两个数字之积是5的倍数的共有3种,根据概率公式即可分别算出数字之积为3的倍数和数字之积为5的倍数的概率。
18.【答案】
解:依题意列表得:
x
y
2
3
4
6
2
(2,3)
(2,4)
(2,6)
3
(3,2)
(3,4)
(3,6)
4
(4,2)
(4,3)
(4,6)
6
(6,2)
(6,3)
(6,4)
由上表可得,点A的坐标共有12种结果,其中点A在反比例函数
上的有4种:
(2,6)、(3,4)、(4,3)、(6,2),∴点A在反比例函数
上的概率为
【解析】根据题意,列出表格,由表可知:点A的坐标共有12种结果,根据反比例函数图像上的点的坐标特点,,其中点A在反比例函数
y
=上的有4种,根据概率公式即可算出点A在反比例函数
y
=上概率。
19.【答案】
(1)解:画树状图如下:
由树形图可知所以可能的结果为AA,AB,AC,BA,BB,BC,CA,CB,CC;
(2)解:由(1)可知两人再次成为同班同学的概率=
【解析】(1)根据题意画出树状图,由图知:所有等可能的结果共有9种,分别为AA,AB,AC,BA,BB,BC,CA,CB,CC;
(2)由(1)知::所有等可能的结果共有9种,其中为同班的只有3种,故根据概率公式即可计算出两人再次成为同班同学的概率。
20.【答案】
(1)解:列表得:
点Q所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种;
(2)解:∵共有12种等可能的结果,其中在函数y=﹣x+6图象上的有2种,即:(2,4),(4,2),
∴点Q(x,y)在函数y=﹣x+6图象上的概率为:P=
【解析】(1)根据题意,李晓同学从布袋里随机取出一个小球,共有4种等可能的结果,张丹同学在剩下的3个小球中随机取出一个小球,共有3种等可能的结果,从而得出:点Q所有可能的坐标共有12种;
(2)根据一次函数图像上的点的坐标特点,12种等可能的结果中在函数y=﹣x+6图象上的只有2种,根据概率公式即可求出点Q(x,y)在函数y=﹣x+6图象上的概率.
21.【答案】
(1)解:3x+4>x,得x>-2,
解
x≤x+
,得x≤2,
∴不等式组的解集为:-2<x≤2,
∴它的所有整数解为-1,0,1,2.
(2)解:画树状图如下:共有12种等可能的结果,积为正数的有2种,
∴积为正数的概率为
=
.
【解析】(1)分别解出不等式组中的每一个不等式的解集,再根据大小小大中间找得出不等式组的解集,再在解集范围内找出整数解;
(2)根据题意,画出树状图,由图知:共有12种等可能的结果,积为正数的有2种,根据概率公式即可求出答案。
22.【答案】
(1)解:所填数字为:120×0.55=66,88÷160=0.55;
折线图:
(2)解:如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,估计这个机会约是0.55.
(3)解:根据(2)的结果估计连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为0.5.
【解析】(1)根据频数等于实验次数乘以频率,及频率等于频数除以实验次数即可算出表中空白数字;根据实验次数及频率的数值,在坐标系中描出格点,再顺次连接即可补全折线统计图;
(2)用频率估计概率,如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,估计这个机会约是0.55;
(3)将该“車”字棋子,按照实验要求连续抛2次,第一次可能车字朝上,也可能朝下,第二次也是可能车字朝上,也可能朝下,出现的所有等可能结果是(上,下)(上,上)(下,上)(下,下)共四种,其中刚好使“車”字一次字面朝上,一次朝下的共有2种,根据概率公式即可算出刚好使“車”字一次字面朝上,一次朝下的可能性。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版2021年九年级上册第2章《简单事件的概率》单元综合测试卷
(满分100分)
一、选择题(共10题;共30分)
1.下列语句描述的事件中,是随机事件的为(??
)
A.?水能载舟,亦能覆舟???????????????????????????????????????????B.?只手遮天,偷天换日
C.?瓜熟蒂落,水到渠成???????????????????????????????????????????D.?心想事成,万事如意
2.一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是必然事件的为(??
)
A.?至少有1个球是黑球??????B.?至少有1个球是白球??????C.?至少有2个球是黑球??????D.?至少有2个球是白球
3.“14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则(??
)
A.?P=0??????????????????????????????????B.?0<P<1??????????????????????????????????C.?P=1??????????????????????????????????D.?P>1
4.王老师对本班40名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别
A型
B型
AB型
O型
频率
0.4
0.35
0.1
0.15
A.?16人?????????????????????????????????????B.?14人?????????????????????????????????????C.?4人?????????????????????????????????????D.?6人
5.从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是(??
)
A.?0???????????????????????????????????????????B.????????????????????????????????????????????C.????????????????????????????????????????????D.?1
6.随机掷一枚质地均匀的硬币两次,落地后至多有一次正面朝下的概率为(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
7.如图,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个开关,使电路形成通路,则使电路形成通路的概率是(??
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
8.甲乙两人轮流在黑板上写下不超过
的正整数(每次只能写一个数),规定禁止在黑板上写已经写过的数的约数,最后不能写的为失败者,如果甲写第一个,那么,甲写数字(
??)时有必胜的策略.
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
9.如果
是随机投掷一枚骰子所得的数字(1,2,3,4,5,6),则关于
的一元二次方程
有两个不等实数根的概率P=
(????
)
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
10.“五一”长假期间,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动,顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据:
转动转盘的次数n
100
150
200
500
800
1000
落在“铅笔”区域的次数m
68
108
140
355
560
690
落在“铅笔”区域的频率
0.68
0.72
0.70
0.71
0.70
0.69
下列说法不正确的是(???
)
A.?当n很大时,估计指针落子在”铅笔“区域的概率大约是0.70
B.?假如你去转动转盘一次,获得“铅笔”概率大约是0.70
C.?如果转动转盘3000次,指针落在“文具盒”区域的次数大约有900次
D.?转动转盘20次,一定有6次获得“文具盒”
二、填空题(共6题;共18分)
11.“同位角相等”,这是________事件(选填“随机”或“必然”).
12.在-1,0,
,
,π,0.10110中任取一个数,取到无理数的概率是________.
13.从
1,2,3,4,5,6,7,8,9,10这十个数中随机取出一个数,取出的数是3的倍数的概率是________.
14.如图,现分别旋转两个标准的转盘,则转盘所转到的两个数字之积为奇数的概率是________
.
15.有五张背面完全相同的卡片,其正面分别画有等腰三角形、平行四边形、矩形、正方形、菱形,将这五张卡片背面朝上洗匀,从中随机抽取一张,卡片上的图形是中心对称图形的概率是________.
16.动物学家通过大量的调查,估计某种动物活到20岁的概率为0.8,活到25岁的概率为0.5,据此若设刚出生的这种动物共有a只.则20年后存活的有________只,现年20岁的这种动物活到25岁的概率是________.
三、解答题(共6题;共52分)
17.有两个可以自由转动的均匀转盘
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).
用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
18.布袋里有四个小球,球表面分别标有2、3、4、6四个数字,它们的材质、形状、大小完全相同。从中随机摸出一个小球记下数字为x,再从剩下的三个球中随机摸出一个球记下数字为y,点A的坐标为(x,y).运用画树状图或列表的方法,写出A点所有可能的坐标,并求出点A在反比例函数
图象上的概率.
19.小明、小林是某中学九年级的同班同学.在三月份举行的自主招生考试中,他俩都被同一所高中提前录取,并被编入A,B,C三个班,他俩希望能两次成为同班同学.
(1)请你用画树状图法或列举法,列出所有可能的结果;
(2)求两人两次成为同班同学的概率.
20.在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,李晓同学从布袋里随机取出一个小球,记下数字为x,张丹同学在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+6图象上的概率.
21.已知不等式组
?
(1)求不等式组的解,并写出它的所有整数解.??
(2)在不等式组的所有整数解中任取两个不同的整数相乘,请用画树状图或列表的方法求积为正数的概率.
22.一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
实验次数
20
40
60
80
100
120
140
160
“車”字朝上的频数
14
18
38
47
52
??
?
?
?
78
88
相应的频率
0.7
0.45
0.63
0.59
0.52
0.55
0.56
?
?
?
?
?
(1)请将表中数据补充完整,并画出折线统计图中剩余部分.
(2)如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,请估计这个机会约是多少?
(3)在(2)的基础上,进一步估计:将该“車”字棋子,按照实验要求连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为多少?
参考答案
一、选择题
1.【答案】
D
【解析】【解答】解:A、水能载舟,亦能覆舟,是必然事件,故不符合题意;
B、只手遮天,偷天换日,是不可能事件,故不符合题意;
C、瓜熟蒂落,水到渠成,是必然事件,故不符合题意;
D、心想事成,万事如意,是随机事件,故符合题意.
故答案为:D.
所谓随机事件,就是可能发生,也可能不会发生的事件,根据概念即可一一判断。
2.【答案】
A
【解析】【解答】至少有1个球是黑球是必然事件,A正确;至少有1个球是白球是随机事件,B不正确;至少有2个球是黑球是随机事件,C不正确;至少有2个球是白球是随机事件,D不正确;故答案为:A.
随机事件是在一定条件下,可能发生也可能不发生的事件;必然事件是在一定条件下,一定发生的事件;不可能事件是在一定条件下,一定不发生的事件;据此判断即可.
3.【答案】
C
【解析】【解答】解:∵一年有12个月,14个人中有12个人在不同的月份过生日,剩下的两人不论哪个月生日,都和前12人中的一个人同一个月过生日
∴“14人中至少有2人在同一个月过生日”是必然事件,
即这一事件发生的概率为
.
故答案为:C.
先确定“14人中至少有2人在同一个月过生日”这一事件为必然事件,从而求出结论.
4.【答案】
A
【解析】【解答】本班A型血的人数为:40×0.4=16.
故选:A.
根据频数和频率的定义求解即可.
5.【答案】
B
【解析】【解答】解:
共有6种情况,积是正数的有2种情况,故概率为
,
故选:B.
列举出所有情况,看积是正数的情况数占总情况数的多少即可.
6.【答案】
A
【解析】【解答】随机掷一枚质地均匀的硬币两次,共“正、反”,“反、正”,“正、正”,“反、反”,4种情况,落地后至多有一次正面朝下包括“正、反”,“反、正”,“正、正”,3种情况,
故至多有一次正面朝下的概率为
.
故答案为:A.
用列举法确定所有等可能的情况,根据落地后至多有一次正面朝下的次数,利用概率公式计算解答.
7.【答案】
C
【解析】【解答】共有5个开关,任意闭合2个,共有5×4÷2=10种情况;在闭合a的情况下,有3种情况出现通路,同理,在闭合b的情况下,也出现3种通路.共有6种通路.∴使电路形成通路的概率是
,
故答案为:C.
找出闭合a,b,c,d,e五个开关中的任意两个开关的所有情况,
再作出只有闭合两条线路里的两个才能形成通路的所有情况,代入概率的计算公式即可求出使电路形成通路的概率
.
8.【答案】
D
【解析】【解答】对于选项A:当甲写10时,乙可以写3、4、6、7、8、9,如果乙写7,则乙必胜,因为无论甲写3,4,6,8,9这五个数中的6(连带3)或8(连带4),乙可以写4或3,剩下2个数字;当甲写3或4时,乙可以写8(连带4)或6(连带3),剩下偶数个数字甲最后不能写,乙必胜;
对于选项B:当甲写9后,乙可以写2、4、5、6、7、8、10,如果乙写6,则乙必胜,因为剩下4、5、7、8、10这5个数中,无论甲写8(连带4)或10(连带5),乙可以写5或4;当甲写4或5时,乙可以写10(连带5)或8(连带4),甲最后不能写,乙必胜;
对于选项C:当甲写8时,乙可以写3、5、6、7、9、10,当乙写6(或10)时,甲就必须写10(或6),因为乙写6(或10)后,连带3(或5)也不能写了,这样才能保证剩下能写的数有偶数个,甲才可以获胜;
对于选项D:
甲先写6,由于6的约数有1,2,3,6,接下来乙可以写的数只有4、5、7、8、9、10,把这6个数分成三组:(4,7)、(5,8)、(9,10),当然也可(4,5)、(8,10)、(7,9)或(4,9)、(5,7)、(8,10)等等,只要组内两数大数不是小数的倍数即可,这样,乙写某组数中的某个数时,甲就写同组中的另一数,从而甲一定写最后一个,甲必获胜,
综上可知,只有甲先写6,才能必胜,
故答案为:D.
根据游戏规则,分别将四个答案,一一分析,判断出最后一个能书写的是谁即可得出答案。
9.【答案】
A
【解析】【解答】∵一元二次方程
有两个不等实数根,
∴
?,
∴k<5且k≠1,
∵
是随机投掷一枚骰子所得的数字(1,2,3,4,5,6),共6种情况
∴能使关于
的一元二次方程
有两个不等实数根的k值为2、3、4,共计3种情况,
∴关于
的一元二次方程
有两个不等实数根的概率P=
=
,
故答案为:A.
根据一元二次方程的定义,二次项的系数不能为0,又此方程有两个不相等的实数根,故根的判别式应该大于0,从而列出不等式组,求解得出k的取值范围,随机投掷一枚骰子所得的数字(1,2,3,4,5,6),共6种情况,能使关于
x
的一元二次方程
(
k
?
1
)
x2
+
4
x
+
1
=
0
有两个不等实数根的k值为2、3、4,共计3种情况,故根据概率公式即可算出答案。
10.【答案】
D
【解析】【解答】A、频率稳定在0.7左右,故用频率估计概率,指针落在“铅笔”区域的频率大约是0.70,故A选项符合题意;
由A可知B、转动转盘一次,获得铅笔的概率大约是0.70,故B选项符合题意;
C、指针落在“文具盒”区域的概率为0.30,转动转盘2000次,指针落在“文具盒”区域的次数大约有3000×0.3=900次,故C选项符合题意;
D、随机事件,结果不确定,故D选项符合题意.
故答案为:D
.
根据图表可求得指针落在铅笔区域的概率,另外概率是多次实验的结果,因此不能说转动转盘20次,一定有6次获得文具盒.
二、填空题
11.【答案】
随机
【解析】【解答】“同位角相等”,这是随机事件.
故答案为:随机.
同位角只有在二直线平行的情况下才相等,如果二直线不平行,则同位角是不相等的,故事随机事件。
12.【答案】
【解析】【解答】共有6个实数,其中无理数有2个,所以取到无理数的概率是
.
故本题应填
.
在这些数中,随机的取出一个数,共有6种等可能的结果,其中能取出无理数的只有两种等可能结果,根据概率公式即可算出取到无理数的概率。
13.【答案】
【解析】【解答】∵1、2、3、4、5、6、7、8、9、10这十个数中,3的倍数的有3、6、9共3个数,
∴取出的数是3的倍数的概率是:
.
故答案为:
从1、2、3、4、5、6、7、8、9、10这十个数中随机的取出一个数字,共有10种等可能的结果,其中是3的倍数的有3、6、9共3种情况,根据概率公式即可算出取出的数是3的倍数的概率。
14.【答案】
【解析】【解答】画树状图得:
∵共有6种等可能的结果,转盘所转到的两个数字之积为奇数的有2种情况,
∴转盘所转到的两个数字之积为奇数的概率是:
.
故答案是:
转动第一个转盘共有两种等可能的结果,转动第二个转盘共有三种等可能的结果,根据题意,画出树状图,由图知:共有6种等可能的结果,转盘所转到的两个数字之积为奇数的有2种情况,根据概率公式即可求出转盘所转到的两个数字之积为奇数的概率。
15.【答案】
【解析】【解答】解:∵等腰三角形、平行四边形、矩形、正方形、菱形中,平行四边形、矩形、正方形、菱形都是中心对称图形,
∴从中随机抽取一张,卡片上的图形是中心对称图形的概率是:
.
故答案为:
.
有五张背面完全相同的卡片,其正面分别画有等腰三角形、平行四边形、矩形、正方形、菱形,将这五张卡片背面朝上洗匀,从中随机抽取一张共有5种等可能的结果,其中是中心对称图形的只有4种,根据概率公式即可得出答案。
16.【答案】
;
【解析】【解答】解:共有a只这种动物
∵这种动物活到20岁的概率为0.8,活到25岁的概率为0.5,
∴这种动物活到20岁的有0.8a只,活到25岁的有0.5a只,
∴现年20岁的这种动物活到25岁的概率是0.5a÷0.8a=
故答案为:
.
先求出这种动物活到20岁的有0.8a只,活到25岁的有0.5a只,再求概率即可。
三、解答题
17.【答案】
解:P(3的倍数)=
P(5的倍数)=
【解析】根据题意,转动转盘A共有3种等可能的结果,转动转盘B也共有3种等可能的结果,根据题意画出树状图,由图知:共有9种等可能的结果,其中两次转动,指针所指的两个数字之积是3的倍数的共有5种,两次转动,指针所指的两个数字之积是5的倍数的共有3种,根据概率公式即可分别算出数字之积为3的倍数和数字之积为5的倍数的概率。
18.【答案】
解:依题意列表得:
x
y
2
3
4
6
2
(2,3)
(2,4)
(2,6)
3
(3,2)
(3,4)
(3,6)
4
(4,2)
(4,3)
(4,6)
6
(6,2)
(6,3)
(6,4)
由上表可得,点A的坐标共有12种结果,其中点A在反比例函数
上的有4种:
(2,6)、(3,4)、(4,3)、(6,2),∴点A在反比例函数
上的概率为
【解析】根据题意,列出表格,由表可知:点A的坐标共有12种结果,根据反比例函数图像上的点的坐标特点,,其中点A在反比例函数
y
=上的有4种,根据概率公式即可算出点A在反比例函数
y
=上概率。
19.【答案】
(1)解:画树状图如下:
由树形图可知所以可能的结果为AA,AB,AC,BA,BB,BC,CA,CB,CC;
(2)解:由(1)可知两人再次成为同班同学的概率=
【解析】(1)根据题意画出树状图,由图知:所有等可能的结果共有9种,分别为AA,AB,AC,BA,BB,BC,CA,CB,CC;
(2)由(1)知::所有等可能的结果共有9种,其中为同班的只有3种,故根据概率公式即可计算出两人再次成为同班同学的概率。
20.【答案】
(1)解:列表得:
点Q所有可能的坐标有:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)共12种;
(2)解:∵共有12种等可能的结果,其中在函数y=﹣x+6图象上的有2种,即:(2,4),(4,2),
∴点Q(x,y)在函数y=﹣x+6图象上的概率为:P=
【解析】(1)根据题意,李晓同学从布袋里随机取出一个小球,共有4种等可能的结果,张丹同学在剩下的3个小球中随机取出一个小球,共有3种等可能的结果,从而得出:点Q所有可能的坐标共有12种;
(2)根据一次函数图像上的点的坐标特点,12种等可能的结果中在函数y=﹣x+6图象上的只有2种,根据概率公式即可求出点Q(x,y)在函数y=﹣x+6图象上的概率.
21.【答案】
(1)解:3x+4>x,得x>-2,
解
x≤x+
,得x≤2,
∴不等式组的解集为:-2<x≤2,
∴它的所有整数解为-1,0,1,2.
(2)解:画树状图如下:共有12种等可能的结果,积为正数的有2种,
∴积为正数的概率为
=
.
【解析】(1)分别解出不等式组中的每一个不等式的解集,再根据大小小大中间找得出不等式组的解集,再在解集范围内找出整数解;
(2)根据题意,画出树状图,由图知:共有12种等可能的结果,积为正数的有2种,根据概率公式即可求出答案。
22.【答案】
(1)解:所填数字为:120×0.55=66,88÷160=0.55;
折线图:
(2)解:如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,估计这个机会约是0.55.
(3)解:根据(2)的结果估计连续抛2次,则刚好使“車”字一次字面朝上,一次朝下的可能性为0.5.
【解析】(1)根据频数等于实验次数乘以频率,及频率等于频数除以实验次数即可算出表中空白数字;根据实验次数及频率的数值,在坐标系中描出格点,再顺次连接即可补全折线统计图;
(2)用频率估计概率,如果实验继续进行下去,根据上表数据,这个实验的频率将接近于该事件发生的机会,估计这个机会约是0.55;
(3)将该“車”字棋子,按照实验要求连续抛2次,第一次可能车字朝上,也可能朝下,第二次也是可能车字朝上,也可能朝下,出现的所有等可能结果是(上,下)(上,上)(下,上)(下,下)共四种,其中刚好使“車”字一次字面朝上,一次朝下的共有2种,根据概率公式即可算出刚好使“車”字一次字面朝上,一次朝下的可能性。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
