2021-2022学年浙教版八年级数学上册1.1 认识三角形 课件(14张PPT)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册1.1 认识三角形 课件(14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 20:38:37 | ||
图片预览










文档简介
(共45张PPT)
1.1
认识三角形(1)
怎样的图形叫三角形?
怎样的图形不叫三角形?
莱洛三角形
线
段
首尾相接,封闭图形
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
三角形的定义
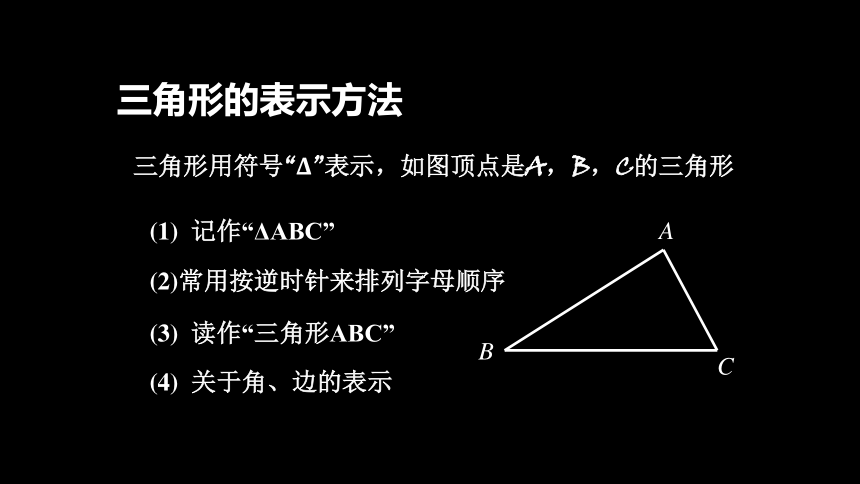
三角形用符号“Δ”表示,如图顶点是A,B,C的三角形
(1)
记作“ΔABC”
(3)
读作“三角形ABC”
(4)
关于角、边的表示
C
B
A
三角形的表示方法
(2)常用按逆时针来排列字母顺序
A
B
C
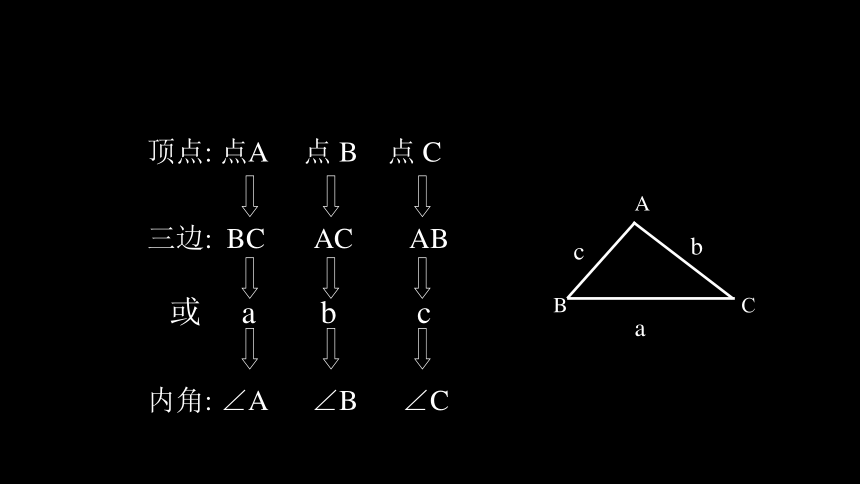
三边:
BC
AC
AB
内角:
∠A
∠B
∠C
顶点:
点A
点
B
点
C
a
c
b
或
a
b
c
1.图中有__个三角形,并写出图中各三角形.
3
2.图中有__个三角形,并写出图中各三角形.
A
C
B
E
D
6
C
B
A
D
你知道任意三角形的内角和是多少度吗?
三角形的内角和180°
C
B
A
Q:如何证明?
如图,在△ABC中,∠A=40°,
∠B=36°,试通过说理的形式求∠C的度数.
C
B
A
变式1:在三角形ABC中,∠A=45°,∠B=
2∠C,求∠B、
∠C的度数。
变式2:在三角形ABC中,∠A=∠B=
2∠C,求∠B、
∠C的度数。
那么任意三角形的外角和是多少度吗?
C
B
A
(1)下图中三角形被遮住的两个内角可能是什么角?将所得结果与(1)的结果进行比较.
三角形按角的大小分类如下:
三角形
直角三角形(有一个内角是直角)
锐角三角形(三个内角都是锐角)
钝角三角形(有一个内角是钝角)
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC”
在三角形中,最多有几个锐角?几个钝角?几个直角呢?
黎曼几何
罗巴切夫斯基几何
欧几里得几何
构成三角形的三边存在怎样的关系?
两点之间线段最短。
在A点的小狗,为了尽快吃到B点的香肠,它选择A
B路线,还是选择A
C
B路线,为什么?
A
C
B
三角形任何两边的和大于第三边.
A
B
C
a
b
c
a+b>c
a+c>b
c+b>a
Q:考虑边界值,左右能相等吗?
长度为6cm,
4cm,
3cm三条线段能否组成三角形?
解:∵
6+4>3
6+3>4
4+3>6
∴能组成三角形
解:
∵最长线段是
6cm
4+3>6
∴能组成三角形
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
判断下列各组线段中,哪些能组成三角形,哪些不能组成三角形,并说明理由。
(1)a=2.5cm,
b=3cm,
c=5cm.
(2)e=6.3cm,
f=6.3cm,
g=12.6cm.
解(1)∵
最长线段是c=5cm,
a+b=2.5+3=5.5(cm)
∴
a+b>c.线段a,b,c能组成三角形。
(2)∵
最长线段是g=12cm,
e+f=6+6=12(cm)
∴
e+f=g.线段e,f,g不能组成三角形。
由下列长度的三条线段能组成三角形吗?
请说明理由.
(1)1cm,2cm,3.5cm
(2)4cm,5cm,9cm
(3)6cm,8cm,13cm
不能
不能
能
2、一个三角形有两边相等,已知其中一边是5cm,另一边是9cm,则这个三角形的周长是______________
3、一个三角形有两边相等,已知其中一边是3cm,另一边是9cm,则这个三角形的周长是______________
21cm
19cm或23cm
换个视角
4
、已知三角形的其中两边长分别为1cm和3cm,且第三边长为整数,则这个三角形的第三边长是________.
Q:边长有没有下限?
A
B
C
a
b
c
a
<
c
+
b
Q:边长下限是多少?
边长有上限
a-b____c;
b-c____a;
a-c____b
<
<
<
三角形任何两边的差小于第三边.
A
B
C
a
b
c
(a>b
>c)
三角形任何两边的和大于第三边
推广
两边之差?第三边?两边之和
已知三角形的两边,
求第三边的取值范围
A
B
C
7
3
如图,如果要构成三角形,求AC的取值范围.
4已知三角形的两边a,b长分别为2和3,则第三边c的范围是_____________
1若三角形的两边长分别为a和b,(设a?b)则第三边c的范围是_____________
.
a-b在△ABC中,AB=7
BC=3
1.若AC为整数,那么△ABC的周长=
______________________________;
2.若周长为奇数,那么AC=
____________;
3.若周长为偶数,那么AC=_______;
6或8
15或16或17或18或19
5或7或9
A
B
C
7
3
小结
2、三角形的三边关系:
(1)判断三条已知线段能否组成三角形.
(2)已知三角形的两边,求第三边的取值范围:
1.用符号字母表示三角形
三角形的内角和
任何两边的和大于第三边
两边之差?第三边?两边之和
如果没有你,我独自站在这里,又是为了什么?
A
B
C
D
3:图中有__个三角形,并写出图中各三角形.
2
4:图中有__个三角形,并写出图中各三角形.
A
B
C
D
O
8
请用最简单的方法说出这两个三角形的三条边和三个内角。
现有木棒4根,长度分别为12,
10,
8,
4,
选其中3根组成三角形,则能组成三角形的个数是(
)
A.1
B.2
C.3
D.4
C
如图,在△ABC中,D是AB
上一点,且AD=AC,连结CD.用
“>”或“<”号填入下面各个
空格,并说明理由。
(1)
AB____AC
+
BC
(2)
2AD____CD;
A
B
D
C
>
<
若三角形的周长为13,且三边长都有是整数,且a≤b≤c,那么满足条件的三角形有多少个?
若三角形的周长为17,且三边长都有是整数,且a≤b≤c,那么满足条件的三角形有多少个?
1.1
认识三角形(1)
怎样的图形叫三角形?
怎样的图形不叫三角形?
莱洛三角形
线
段
首尾相接,封闭图形
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
三角形的定义
三角形用符号“Δ”表示,如图顶点是A,B,C的三角形
(1)
记作“ΔABC”
(3)
读作“三角形ABC”
(4)
关于角、边的表示
C
B
A
三角形的表示方法
(2)常用按逆时针来排列字母顺序
A
B
C
三边:
BC
AC
AB
内角:
∠A
∠B
∠C
顶点:
点A
点
B
点
C
a
c
b
或
a
b
c
1.图中有__个三角形,并写出图中各三角形.
3
2.图中有__个三角形,并写出图中各三角形.
A
C
B
E
D
6
C
B
A
D
你知道任意三角形的内角和是多少度吗?
三角形的内角和180°
C
B
A
Q:如何证明?
如图,在△ABC中,∠A=40°,
∠B=36°,试通过说理的形式求∠C的度数.
C
B
A
变式1:在三角形ABC中,∠A=45°,∠B=
2∠C,求∠B、
∠C的度数。
变式2:在三角形ABC中,∠A=∠B=
2∠C,求∠B、
∠C的度数。
那么任意三角形的外角和是多少度吗?
C
B
A
(1)下图中三角形被遮住的两个内角可能是什么角?将所得结果与(1)的结果进行比较.
三角形按角的大小分类如下:
三角形
直角三角形(有一个内角是直角)
锐角三角形(三个内角都是锐角)
钝角三角形(有一个内角是钝角)
直角三角形可以用符号“Rt△”表示,直角三角形ABC可以写成“Rt△ABC”
在三角形中,最多有几个锐角?几个钝角?几个直角呢?
黎曼几何
罗巴切夫斯基几何
欧几里得几何
构成三角形的三边存在怎样的关系?
两点之间线段最短。
在A点的小狗,为了尽快吃到B点的香肠,它选择A
B路线,还是选择A
C
B路线,为什么?
A
C
B
三角形任何两边的和大于第三边.
A
B
C
a
b
c
a+b>c
a+c>b
c+b>a
Q:考虑边界值,左右能相等吗?
长度为6cm,
4cm,
3cm三条线段能否组成三角形?
解:∵
6+4>3
6+3>4
4+3>6
∴能组成三角形
解:
∵最长线段是
6cm
4+3>6
∴能组成三角形
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
判断下列各组线段中,哪些能组成三角形,哪些不能组成三角形,并说明理由。
(1)a=2.5cm,
b=3cm,
c=5cm.
(2)e=6.3cm,
f=6.3cm,
g=12.6cm.
解(1)∵
最长线段是c=5cm,
a+b=2.5+3=5.5(cm)
∴
a+b>c.线段a,b,c能组成三角形。
(2)∵
最长线段是g=12cm,
e+f=6+6=12(cm)
∴
e+f=g.线段e,f,g不能组成三角形。
由下列长度的三条线段能组成三角形吗?
请说明理由.
(1)1cm,2cm,3.5cm
(2)4cm,5cm,9cm
(3)6cm,8cm,13cm
不能
不能
能
2、一个三角形有两边相等,已知其中一边是5cm,另一边是9cm,则这个三角形的周长是______________
3、一个三角形有两边相等,已知其中一边是3cm,另一边是9cm,则这个三角形的周长是______________
21cm
19cm或23cm
换个视角
4
、已知三角形的其中两边长分别为1cm和3cm,且第三边长为整数,则这个三角形的第三边长是________.
Q:边长有没有下限?
A
B
C
a
b
c
a
<
c
+
b
Q:边长下限是多少?
边长有上限
a-b____c;
b-c____a;
a-c____b
<
<
<
三角形任何两边的差小于第三边.
A
B
C
a
b
c
(a>b
>c)
三角形任何两边的和大于第三边
推广
两边之差?第三边?两边之和
已知三角形的两边,
求第三边的取值范围
A
B
C
7
3
如图,如果要构成三角形,求AC的取值范围.
4
1
.
a-b
BC=3
1.若AC为整数,那么△ABC的周长=
______________________________;
2.若周长为奇数,那么AC=
____________;
3.若周长为偶数,那么AC=_______;
6或8
15或16或17或18或19
5或7或9
A
B
C
7
3
小结
2、三角形的三边关系:
(1)判断三条已知线段能否组成三角形.
(2)已知三角形的两边,求第三边的取值范围:
1.用符号字母表示三角形
三角形的内角和
任何两边的和大于第三边
两边之差?第三边?两边之和
如果没有你,我独自站在这里,又是为了什么?
A
B
C
D
3:图中有__个三角形,并写出图中各三角形.
2
4:图中有__个三角形,并写出图中各三角形.
A
B
C
D
O
8
请用最简单的方法说出这两个三角形的三条边和三个内角。
现有木棒4根,长度分别为12,
10,
8,
4,
选其中3根组成三角形,则能组成三角形的个数是(
)
A.1
B.2
C.3
D.4
C
如图,在△ABC中,D是AB
上一点,且AD=AC,连结CD.用
“>”或“<”号填入下面各个
空格,并说明理由。
(1)
AB____AC
+
BC
(2)
2AD____CD;
A
B
D
C
>
<
若三角形的周长为13,且三边长都有是整数,且a≤b≤c,那么满足条件的三角形有多少个?
若三角形的周长为17,且三边长都有是整数,且a≤b≤c,那么满足条件的三角形有多少个?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
