2021-2022学年浙教版八年级数学上册2.1 图形的轴对称 课件(17张PPT)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册2.1 图形的轴对称 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 20:41:06 | ||
图片预览






文档简介
(共17张PPT)
2.1
图形的轴对称
北京故宫
探究新知
欣赏以下优美的图片,
它们有什么共同特点?
凯旋门
你还能从生活中或者我们学过的几何图形中举出哪些例子?
阅读课本48页第一段文字,圈出关键词语,并尝试完成课本48页合作学习1
探究归纳
1.轴对称图形:如果把一个图形沿着一条直线折叠后,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形;
2.对称轴:这条直线叫做对称轴.
定义:
动手操作--轴对称图形
1.在下发的印有几何图形的纸上剪下几何图形,并通过折一折,画一画找到它的对称轴.
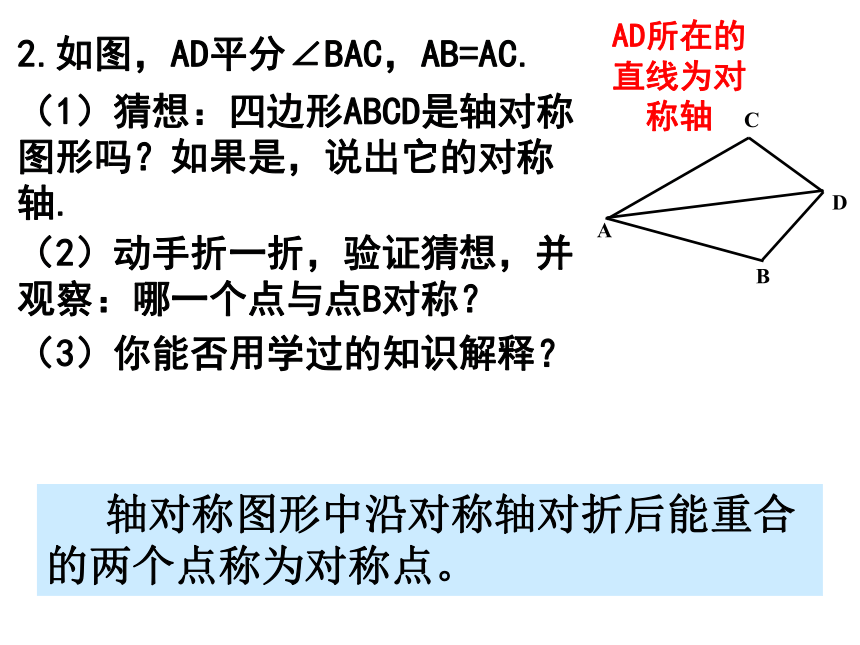
2.如图,AD平分∠BAC,AB=AC.
A
B
C
D
AD所在的直线为对称轴
轴对称图形中沿对称轴对折后能重合的两个点称为对称点。
(1)猜想:四边形ABCD是轴对称图形吗?如果是,说出它的对称轴.
(2)动手折一折,验证猜想,并观察:哪一个点与点B对称?
(3)你能否用学过的知识解释?
2.如图,AD平分∠BAC,AB=AC.连结BC,交AD于点E.
(6)由AC=AB,CD=BD,可得对称轴AD与对称点的连线BC有何关系?尝试概括。
轴对称图形的性质:
对称轴垂直平分连结两个对称点的线段.
E
A
B
C
D
(4)把四边形ABCD沿AD对折,图中重合的线段有哪些?
(5)图中重合的角有哪些?
1、垂直
第一关
已知直线m和点A,以直线m为对称轴,作出点A的对称点A’.
A
2、延长
A'
m
点A’就是所求的点。
虚线
你会画吗?
3、相等
第二关
已知直线m和线段AB,以直线m为对称轴,作出以A,B的对称点A’,
B’为端点的线段A’B’
A'
B'
A
B
m
线段A’B’就是所求的线段。
实线
你会画吗?
m
如图,已知△ABC和直线m。以直线m为对称
轴,求作以点A,B,C的对称点A’,B’,C’为顶
点的△
A’B’C’
第三关
A
B
C
你会画吗?
一般的,由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够互相重合,这样的图形改变叫做图形的轴对称,这条直线叫做对称轴.
图形的轴对称
图形的轴对称有下面的性质:
1、成轴对称的图形不改变原图形的形状和大小.
2、成轴对称的两个图形是全等图形.
请同学们观察刚才画的两个三角形,以及下面几组图形,有什么共同特征?
做一做--图形的轴对称
课本52页做一做1、2
例2
如图,直线l表示草原上的一条河流.一骑马少年从A地出发,去河边让马饮水,然后返回位于B地的家中.
他沿怎样的路线行走,能使路程最短?作出这条最短路线.
思考:
2.A,B两点连线是否经过l上一点?为什么?
3.l的另一侧是否存在点A',使l上的任意一点P满足PA=PA'?此时点A与A'有何位置关系?
4.由此,你能顺利解决问题了吗?
1.关于“最短”,你学过哪些相关知识?
解:作点A关于直线l的对称点A’,连结A’B,
交直线l于点C,连结AC,骑马少年沿折线A-C-B的路线行走时路程最短.
证明:设P是直线l上任意一点,连结AP,A'P.
由作图知,直线l垂直平分AA',
则AC=A'C,AP=A'P(线段垂直平分线上的点到线段两端的距离相等)
.
∴AP+BP=A'P+BP≧A'B,
A'B=A'C+BC=AC+BC,
即AP+BP≧AC+BC
所以沿折线A-C-B的路线行走时路程最短.
1、轴对称图形
2、轴对称图形的性质
3、图形的轴对称
4、图形的轴对称的性质
课堂小结
思考:对比轴对称图形和图形的轴对称,它们有何区别与联系?
2.1
图形的轴对称
北京故宫
探究新知
欣赏以下优美的图片,
它们有什么共同特点?
凯旋门
你还能从生活中或者我们学过的几何图形中举出哪些例子?
阅读课本48页第一段文字,圈出关键词语,并尝试完成课本48页合作学习1
探究归纳
1.轴对称图形:如果把一个图形沿着一条直线折叠后,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形;
2.对称轴:这条直线叫做对称轴.
定义:
动手操作--轴对称图形
1.在下发的印有几何图形的纸上剪下几何图形,并通过折一折,画一画找到它的对称轴.
2.如图,AD平分∠BAC,AB=AC.
A
B
C
D
AD所在的直线为对称轴
轴对称图形中沿对称轴对折后能重合的两个点称为对称点。
(1)猜想:四边形ABCD是轴对称图形吗?如果是,说出它的对称轴.
(2)动手折一折,验证猜想,并观察:哪一个点与点B对称?
(3)你能否用学过的知识解释?
2.如图,AD平分∠BAC,AB=AC.连结BC,交AD于点E.
(6)由AC=AB,CD=BD,可得对称轴AD与对称点的连线BC有何关系?尝试概括。
轴对称图形的性质:
对称轴垂直平分连结两个对称点的线段.
E
A
B
C
D
(4)把四边形ABCD沿AD对折,图中重合的线段有哪些?
(5)图中重合的角有哪些?
1、垂直
第一关
已知直线m和点A,以直线m为对称轴,作出点A的对称点A’.
A
2、延长
A'
m
点A’就是所求的点。
虚线
你会画吗?
3、相等
第二关
已知直线m和线段AB,以直线m为对称轴,作出以A,B的对称点A’,
B’为端点的线段A’B’
A'
B'
A
B
m
线段A’B’就是所求的线段。
实线
你会画吗?
m
如图,已知△ABC和直线m。以直线m为对称
轴,求作以点A,B,C的对称点A’,B’,C’为顶
点的△
A’B’C’
第三关
A
B
C
你会画吗?
一般的,由一个图形变为另一个图形,并使这两个图形沿某一条直线折叠后能够互相重合,这样的图形改变叫做图形的轴对称,这条直线叫做对称轴.
图形的轴对称
图形的轴对称有下面的性质:
1、成轴对称的图形不改变原图形的形状和大小.
2、成轴对称的两个图形是全等图形.
请同学们观察刚才画的两个三角形,以及下面几组图形,有什么共同特征?
做一做--图形的轴对称
课本52页做一做1、2
例2
如图,直线l表示草原上的一条河流.一骑马少年从A地出发,去河边让马饮水,然后返回位于B地的家中.
他沿怎样的路线行走,能使路程最短?作出这条最短路线.
思考:
2.A,B两点连线是否经过l上一点?为什么?
3.l的另一侧是否存在点A',使l上的任意一点P满足PA=PA'?此时点A与A'有何位置关系?
4.由此,你能顺利解决问题了吗?
1.关于“最短”,你学过哪些相关知识?
解:作点A关于直线l的对称点A’,连结A’B,
交直线l于点C,连结AC,骑马少年沿折线A-C-B的路线行走时路程最短.
证明:设P是直线l上任意一点,连结AP,A'P.
由作图知,直线l垂直平分AA',
则AC=A'C,AP=A'P(线段垂直平分线上的点到线段两端的距离相等)
.
∴AP+BP=A'P+BP≧A'B,
A'B=A'C+BC=AC+BC,
即AP+BP≧AC+BC
所以沿折线A-C-B的路线行走时路程最短.
1、轴对称图形
2、轴对称图形的性质
3、图形的轴对称
4、图形的轴对称的性质
课堂小结
思考:对比轴对称图形和图形的轴对称,它们有何区别与联系?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
