2021-2022学年浙教版八年级数学上册5.2 函数 课件(19张PPT)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册5.2 函数 课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 504.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 20:45:23 | ||
图片预览




文档简介
(共17张PPT)
5.2
函数(1)
浙教版八年级上册
工作时间t(时)
0
1
2
5
10
…
t
…
报酬m(元)
0
2、怎样用t的代数式表示m?
12
24
60
120
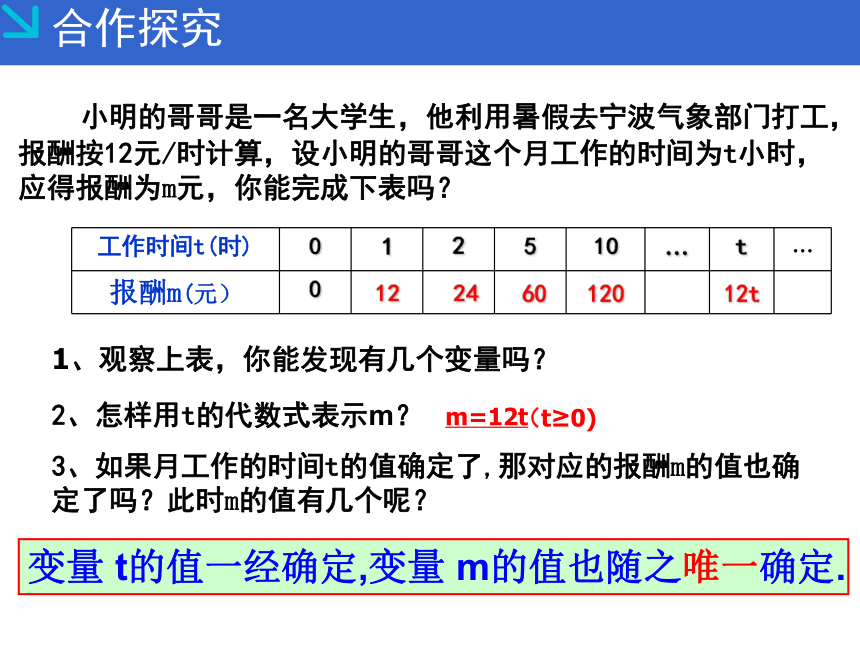
小明的哥哥是一名大学生,他利用暑假去宁波气象部门打工,报酬按12元/时计算,设小明的哥哥这个月工作的时间为t小时,应得报酬为m元,你能完成下表吗?
1、观察上表,你能发现有几个变量吗?
3、如果月工作的时间t的值确定了,那对应的报酬m的值也确定了吗?此时m的值有几个呢?
m=12t
(t≥0)
12t
变量
t的值一经确定,变量
m的值也随之唯一确定.
合作探究
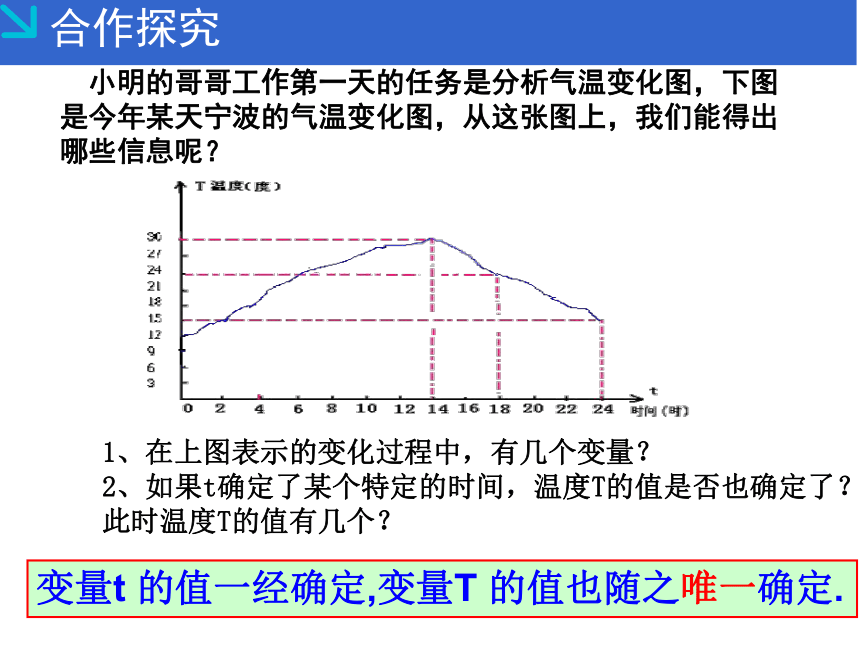
1、在上图表示的变化过程中,有几个变量?
2、如果t确定了某个特定的时间,温度T的值是否也确定了?此时温度T的值有几个?
小明的哥哥工作第一天的任务是分析气温变化图,下图是今年某天宁波的气温变化图,从这张图上,我们能得出哪些信息呢?
变量t
的值一经确定,变量T
的值也随之唯一确定.
合作探究
宁波某建筑材料公司为气象局新的楼房建设提供部分材料。
设每吨材料售价为a(元),该公司的月利润为w(万元).
下表是售价a和月利润w的关系:
售价a(元/吨)
255
250
240
230
220
210
月利润w(万元)
403
405
406
403
396
385
1、观察上表,你能发现有几个变量吗?
2、如果售价a确定了,月利润w的值确定了吗?
此时w的值有几个?
变量a
的值一经确定,变量w
的值也随之唯一确定.
合作探究
售价a(元/吨)
255
250
240
230
220
210
月利润W(万元)
403
405
406
403
396
385
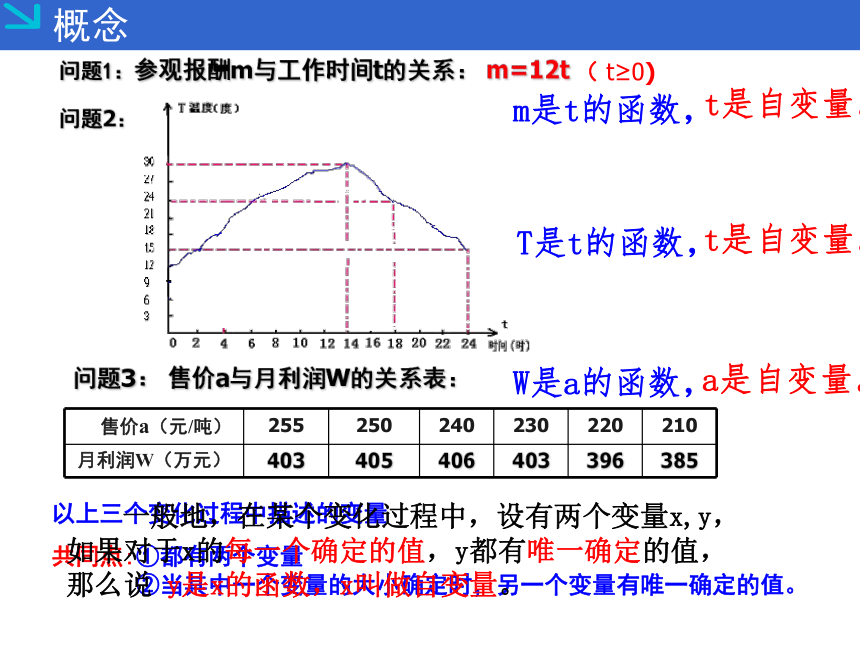
问题1:参观报酬m与工作时间t的关系:
m=12t
问题2:
问题3:
售价a与月利润W的关系表:
以上三个变化过程中描述的变量
共同点:①都有两个变量
②当其中一个变量的大小确定时,另一个变量有唯一确定的值。
一般地,在某个变化过程中,设有两个变量x,y,
如果对于x的每一个确定的值,y都有唯一确定的值,
那么说
y是x的函数,x叫做自变量。
(
t≥0)
m是t的函数,
t是自变量。
T是t的函数,
t是自变量。
W是a的函数,
a是自变量。
概念
1.判断,下列变量中,y是x函数的函数吗?
②
巩固练习
2.判断,下列变量中,y是x函数的函数吗?
⑤
x
-1
0
1
2
3
4
5
…
y
-3
-1
1
3
5
7
9
…
x
0
1
1
2
2
3
3
…
y
0
-1
1
-2
2
-3
3
…
巩固练习
X
Y
P(
x
,y
)
o
3.判断,下列变量中,y是x函数的函数吗?
.
巩固练习
4.判断,下列变量中,y是x函数的函数吗?
⑦
1
2
3
4
5
6
7
1
2
3
4
5
y
O
1
1
5
2
4
6
3
2
3
4
5
x
.
P(
x
,y
)
巩固练习
列表法
售价?(元/吨)
255
250
240
230
220
210
月利润W(万元)
403
405
406
403
396
385
函数的常用表示方法:解析法,图象法,列表法
(1)小明的哥哥一个月工作了150小时,累计的工资是多少?
(2)上午10时,该天温度是多少?
(3)售价为220元时,月利润是多少?
想一想
结合上面函数关系的不同表示方法,回答
函数的值
函数表达式
解析法
问题1:报酬m与工作时间t的关系:
m=12t
问题2:
问题3:
售价与月利润W的关系表:
图象法
函数的常用表示方法
解析法
图象法
列表法
求函数值
代一代
求函数值
画一画
求函数值
查一查
(
t≥0)
函数的表示法
求解函数值
2.某市居民生活用水的价格是2.9元/立方米,设一户居民这个月的用水量为n立方米,应付水费为m元.在这个问题中,m关于n的函数表达式是________;当n=15时,函数值是_____,这个函数值的函数值的实际意义是_____________.
1.求下列函数当时
的函数值
(1)
(2)
(3)
(1)
根据某日的气温变化图,你能分别求出当t为6点、10点时的函数值吗?
(2)
什么时间温度最高,最高温度是多少?
(3)
在什么时间内,
温度在上升?
某日气温变化分析图
-1
2
5
14
—————
3
求解函数值
列函数表达式
1.某市民用水费的价格是1.2元/立方米,小红准备收取她所居住大楼各用户这个月的水费,设用水量为n立方米,应付水费为m元,在这个问题中,m关于n的函数解析式是
。
2.汽车以70km/h的速度由A地驶往
相距360km的B地,设汽车行驶的时间为t(h),离B地的距离为s(km)则s关于t的函数解析式是
。
m=1.2n
s=360-70x
课堂小结
1.函数的概念
2.函数的三种表示方式
3.函数值的概念
今天我们学习了……
基础知识
基本技能
数学思想
1.求函数值
2.列函数表达式
数形结合思想
3.某市民用水费的价格是2.9元/立方米,设小明的哥哥用水量为n立方米,应付水费为m元。
(1)题中变量有________,其中_____是_____的函数,
自变量是_________
(3)当
n=10
时,
m
的值为________
(4)当
m=58
时,n
的值为________
m,n
m
n
n
29
20
(2)m关于n的函数解析式为_________________
m=2.9n
(n≥0)
拓展提高
(2)你还能提出怎样的数学问题?
(1)
y是x的函数吗?
为什么?
2.40
1.60
0.80
邮资y(元)
40<x≤60
20<x≤40
0<x≤20
信件质量x(克)
5.在国内投寄平信应付邮资如下表:
6.如图是宁波市拨打市内电话收费情况,根据图象,我们可以看出:
(1)通话2分钟时的话费为
元。
(2)通话3分钟内,话费是
元,若超过3分钟,话费随时间的增大而
,超过3分钟部分每分钟话费_______。
(3)求当t=4时的函数值,并说明它的实际意义。
0.2
0.2
增大
0.1元
5.2
函数(1)
浙教版八年级上册
工作时间t(时)
0
1
2
5
10
…
t
…
报酬m(元)
0
2、怎样用t的代数式表示m?
12
24
60
120
小明的哥哥是一名大学生,他利用暑假去宁波气象部门打工,报酬按12元/时计算,设小明的哥哥这个月工作的时间为t小时,应得报酬为m元,你能完成下表吗?
1、观察上表,你能发现有几个变量吗?
3、如果月工作的时间t的值确定了,那对应的报酬m的值也确定了吗?此时m的值有几个呢?
m=12t
(t≥0)
12t
变量
t的值一经确定,变量
m的值也随之唯一确定.
合作探究
1、在上图表示的变化过程中,有几个变量?
2、如果t确定了某个特定的时间,温度T的值是否也确定了?此时温度T的值有几个?
小明的哥哥工作第一天的任务是分析气温变化图,下图是今年某天宁波的气温变化图,从这张图上,我们能得出哪些信息呢?
变量t
的值一经确定,变量T
的值也随之唯一确定.
合作探究
宁波某建筑材料公司为气象局新的楼房建设提供部分材料。
设每吨材料售价为a(元),该公司的月利润为w(万元).
下表是售价a和月利润w的关系:
售价a(元/吨)
255
250
240
230
220
210
月利润w(万元)
403
405
406
403
396
385
1、观察上表,你能发现有几个变量吗?
2、如果售价a确定了,月利润w的值确定了吗?
此时w的值有几个?
变量a
的值一经确定,变量w
的值也随之唯一确定.
合作探究
售价a(元/吨)
255
250
240
230
220
210
月利润W(万元)
403
405
406
403
396
385
问题1:参观报酬m与工作时间t的关系:
m=12t
问题2:
问题3:
售价a与月利润W的关系表:
以上三个变化过程中描述的变量
共同点:①都有两个变量
②当其中一个变量的大小确定时,另一个变量有唯一确定的值。
一般地,在某个变化过程中,设有两个变量x,y,
如果对于x的每一个确定的值,y都有唯一确定的值,
那么说
y是x的函数,x叫做自变量。
(
t≥0)
m是t的函数,
t是自变量。
T是t的函数,
t是自变量。
W是a的函数,
a是自变量。
概念
1.判断,下列变量中,y是x函数的函数吗?
②
巩固练习
2.判断,下列变量中,y是x函数的函数吗?
⑤
x
-1
0
1
2
3
4
5
…
y
-3
-1
1
3
5
7
9
…
x
0
1
1
2
2
3
3
…
y
0
-1
1
-2
2
-3
3
…
巩固练习
X
Y
P(
x
,y
)
o
3.判断,下列变量中,y是x函数的函数吗?
.
巩固练习
4.判断,下列变量中,y是x函数的函数吗?
⑦
1
2
3
4
5
6
7
1
2
3
4
5
y
O
1
1
5
2
4
6
3
2
3
4
5
x
.
P(
x
,y
)
巩固练习
列表法
售价?(元/吨)
255
250
240
230
220
210
月利润W(万元)
403
405
406
403
396
385
函数的常用表示方法:解析法,图象法,列表法
(1)小明的哥哥一个月工作了150小时,累计的工资是多少?
(2)上午10时,该天温度是多少?
(3)售价为220元时,月利润是多少?
想一想
结合上面函数关系的不同表示方法,回答
函数的值
函数表达式
解析法
问题1:报酬m与工作时间t的关系:
m=12t
问题2:
问题3:
售价与月利润W的关系表:
图象法
函数的常用表示方法
解析法
图象法
列表法
求函数值
代一代
求函数值
画一画
求函数值
查一查
(
t≥0)
函数的表示法
求解函数值
2.某市居民生活用水的价格是2.9元/立方米,设一户居民这个月的用水量为n立方米,应付水费为m元.在这个问题中,m关于n的函数表达式是________;当n=15时,函数值是_____,这个函数值的函数值的实际意义是_____________.
1.求下列函数当时
的函数值
(1)
(2)
(3)
(1)
根据某日的气温变化图,你能分别求出当t为6点、10点时的函数值吗?
(2)
什么时间温度最高,最高温度是多少?
(3)
在什么时间内,
温度在上升?
某日气温变化分析图
-1
2
5
14
—————
3
求解函数值
列函数表达式
1.某市民用水费的价格是1.2元/立方米,小红准备收取她所居住大楼各用户这个月的水费,设用水量为n立方米,应付水费为m元,在这个问题中,m关于n的函数解析式是
。
2.汽车以70km/h的速度由A地驶往
相距360km的B地,设汽车行驶的时间为t(h),离B地的距离为s(km)则s关于t的函数解析式是
。
m=1.2n
s=360-70x
课堂小结
1.函数的概念
2.函数的三种表示方式
3.函数值的概念
今天我们学习了……
基础知识
基本技能
数学思想
1.求函数值
2.列函数表达式
数形结合思想
3.某市民用水费的价格是2.9元/立方米,设小明的哥哥用水量为n立方米,应付水费为m元。
(1)题中变量有________,其中_____是_____的函数,
自变量是_________
(3)当
n=10
时,
m
的值为________
(4)当
m=58
时,n
的值为________
m,n
m
n
n
29
20
(2)m关于n的函数解析式为_________________
m=2.9n
(n≥0)
拓展提高
(2)你还能提出怎样的数学问题?
(1)
y是x的函数吗?
为什么?
2.40
1.60
0.80
邮资y(元)
40<x≤60
20<x≤40
0<x≤20
信件质量x(克)
5.在国内投寄平信应付邮资如下表:
6.如图是宁波市拨打市内电话收费情况,根据图象,我们可以看出:
(1)通话2分钟时的话费为
元。
(2)通话3分钟内,话费是
元,若超过3分钟,话费随时间的增大而
,超过3分钟部分每分钟话费_______。
(3)求当t=4时的函数值,并说明它的实际意义。
0.2
0.2
增大
0.1元
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
