2021-2022学年浙教版七年级数学上册5.4 一元一次方程的应用课件(23张PPT)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学上册5.4 一元一次方程的应用课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 715.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-06 20:57:57 | ||
图片预览








文档简介
(共23张PPT)
一元一次方程的应用
列方程解应用题的一般步骤是什么?
审——设——列——解——答(验)
注意事项:
1
在一道应用题中,往往含有几个未知数,应恰当的选择其中的一个,用x表示出来,然后根据数量之间的关系,将其他的几个未知量用含x的代数式表示出来。一般题目问什么,就设什么为x,但也会有例外;
2
方程两边要注意单位统一。
3
对于求得的解,还要看它是否符合实际意义,再写出答案
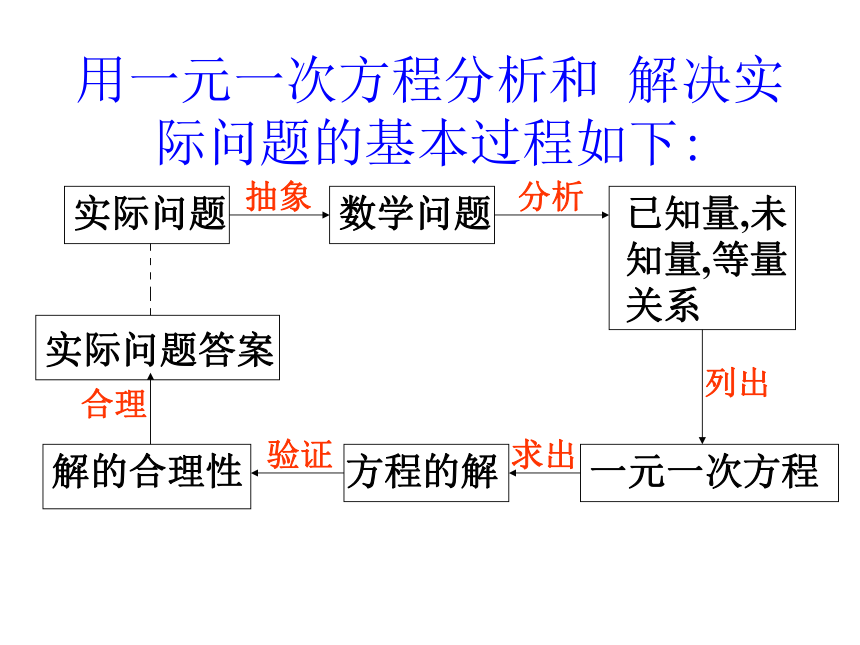
用一元一次方程分析和
解决实际问题的基本过程如下:
实际问题
数学问题
已知量,未知量,等量关系
一元一次方程
方程的解
解的合理性
实际问题答案
抽象
分析
列出
求出
验证
合理
1、甲、乙两地相距162公里,一列慢车从甲站开出,每小时走48公里,一列快车从乙站开出,每小时走60公里试问:
1)两列火车同时相向而行,多少时间可以相遇?
2)两车同时反向而行,几小时后两车相距270公里?
3)若两车相向而行,慢车先开出1小时,再用多少时间
两车才能相遇?
4)若两车相向而行,快车先开25分钟,快车开了几小时
与慢车相遇?
5)两车同时同向而行(快车在后面),几小时后快车
可以追上慢车?
6)两车同时同向而行(慢车在后面),几小时后两车相
距200公里?
一、相遇问题的基本题型
1、同时出发(两段)
二、相遇问题的等量关系
2、不同时出发
(三段
)
一、明确行程问题中三个量的关系
三个基本量关系是:速度×时间=路程
一、追及问题的基本题型
1、不同地点同时出发
二、追及问题的等量关系
2、同地点不同时出发
1、追及时快者行驶的路程-慢者行驶的路程=相距的
路程
2、追及时快者行驶的路程=慢者行驶的路程或
慢者所用时间=快者所用时间+多用时间
从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?
解:设水路长为x千米,则公路长为(x+40)千米
等量关系:船行时间-车行时间=3小时
答:水路长240千米,公路长为280千米,车行时间为
7小时,船行时间为10小时
依题意得:
x+40=280,
x=240
练习:1、两地相距28公里,小明以15公里/小时的速度。小亮以30公里/小时的速度,分别骑自行车和开汽车从同一地
前往另一地,小明先出发1小时,小亮几小时后才能
追上小明?
解:设小亮开车x
小时后才能追上小明,则小亮所行路
程为30x公里,小明所行路程为15(x+1)
等量关系:小亮所走路程=小明所走路程
依题意得:30x=15(x+1)
x=1
检验:两地相距28公里,在两地之间,小亮追不上小明
例题讲解:
例
汽船从甲地顺水开往乙地,所用时间比从乙地逆水
开往甲地少1.5小时。已知船在静水的速度为18千米/小时,
水流速度为2千米/小时,求甲、乙两地之间的距离?
分析:本题是行程问题,但涉及水流速度,必须要
掌握:顺水速度=船速+水速
逆水速度=船速-水速
解:(直接设元)
设甲、乙两地的距离为x
千米
等量关系:逆水所用时间-顺水所用时间=1.5
依题意得:
x=120
答:甲、乙两地的距离为120千米。
例
一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时。已知水流的速度是3千米/时,求船在静水中的速度。
分析:题中的等量关系为
这艘船往返的路程相等,即:
顺流速度×顺流时间=逆流速度×逆流时间
例
一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时。已知水流的速度是3千米/时,求船在静水中的速度。
解:设船在静水中的平均速度为x千米/时,则顺流速度为(x+3)千米/时,逆流速度为(x-3)千米/时。
根据往返路程相等,列得
2(x+3)=2.5(x-3)
去括号,得
2x+6=2.5x-7.5
移项及合并,得
0.5x=13.5
X=27
答:船在静水中的平均速度为27千米/时。
练习:
1、一架飞机飞行两城之间,顺风时需要5小时30分钟,
逆风时需要6小时,已知风速为每小时24公里,
求两城之间的距离?
等量关系:顺风时飞机本身速度=逆风时飞机本身速度。
答:两城之间的距离为3168公里
注:飞行问题也是行程问题。同水流问题一样,飞行问
题的等量关系有:顺风飞行速度=飞机本身速度+风速
逆风飞行速度=飞机本身速度-风速
依题意得:
x=3168
解:设两城之间距离为x
公里,则顺风速为
公
里/小时,逆风速为
公里/小时
小结:
行程问题包括相遇、追击和飞行、航行的速度问题其基本关系是:路程=时间×速度
相遇问题的等量关系:甲行距离+乙行距离=总路程
追击问题的等量关系:
1)同时不同地
:
慢者行的距离+两者之间的距离=快者行的距离
2)同地不同时:
甲行距离=乙行距离
或
慢者所用时间=快者所用时间+多用时间
顺水逆水的问题的等量关系:
1)顺水的路程
=
逆水的路程
2)顺速
–
逆速
=
2水速;顺速
+
逆速
=
2船速
调配问题中的数量关系:
1.无论调配前后总量是否改变,调配后两量之间总有新的倍比关系,解这类题要注意分析调配后两个量之间的关系,从而找到等量关系。
2.关注调配前后总量的变化以及调配后两量之间出现的新的倍比关系,从而找到等量关系。
例5、
甲煤矿有煤432吨。乙煤矿有煤96吨,为了使甲煤矿存煤数是乙煤矿的2倍。应从甲煤矿运多少吨煤到乙煤矿?
分析:数量关系可用表来表示,看得更清楚,更直观。
原有煤量
调运煤量
调后存煤量
等量关系
煤
矿
甲
矿
乙
矿
涉及的量
432
96
-
x
+
x
432
-
x
96
+
x
调后甲矿存煤量=2×调后乙矿存煤量
解:设应从甲煤矿调运
x
吨煤到乙煤矿,那么调运后甲煤矿有煤(432-
x
)吨,
乙煤矿有煤(96
+
x
)吨,根据题意得:
432-x
=
2(96+x)
432-x
=
192+2x,
3x
=
240
X
=
80
答:应从甲煤矿调运80吨煤到乙煤矿。
、某部队开展支农活动,甲队27人,乙队19人,现另调26人去支援,使甲队是乙队的2倍,问应调往甲队、乙队各多少人?
解:设调往甲队x人,则调往乙队(26-x)人
根据题意,得方程:
解方程得:x
=
21
答:调往甲队21人。调往乙队5人。
练习2:甲槽有水34升,乙槽有水18升.现在两槽同时排水,都是平均每分排出2升.多少分钟后,甲槽的水是乙槽的水的3倍?
练习1:将全班45名同学分成两组植树,要求甲组每人挖5个坑,乙组每人挖3个坑并植7棵树,如何分配两组的人数,才能使挖的坑数与植树的棵数相等?
?
工程问题中的数量关系:
1)
工作效率=
工作总量
完成工作总量的时间
———————————
2)工作总量=工作效率×工作时间
3)工作时间=
工作总量
—————
工作效率
4)各队合作工作效率=各队工作效率之和
5)全部工作量之和=各队工作量之和
例题讲解
例1
挖一条长为1200米长的水渠,由甲施工队独做需要30
天完成,乙施工队独做需要20天完成,现在甲、乙两
施工队从两头同时施工,挖完这条水渠估计需几天?
等量关系:
甲施工队挖的米数+乙施工队挖的米数=1200米
答:两个施工队合作估计需要12天挖完。
解:设挖完这条水渠估计要x天.
依题意得
例2
修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独
承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解:
1)设两工程队合作需要x天完成。
2)设修好这条公路共需要
y
天完成。
等量关系:
甲30天工作量+乙队y天的工作量
=
1
答:两工程队合作需要48天完成,修好这条公路还需75天。
等量关系:甲工作量+乙工作量=1
依题意得
依题意得
y=75
x=48
等量关系:4天的工作量+改进后(x
–
4)工作量=
0.5
解:设一共x天可以修完它的一半。
依题意得
×4+
(x—4)=
0.5
答:一共
天可以修完它的一半。
例3
分析:
x=
例4
已知开管注水缸,10分钟可满,拨开底塞,满缸水20
分钟流完,现若管、塞同开,若干时间后,将底塞塞
住,又过了2倍的时间才注满水缸,求管塞同开的时
间是几分钟?
分析:
注入或放出率
注入或放出时间
注入或放出量
注入
放出
解:设两管同开x分钟
等量关系:注入量-放出量=缸的容量
依题意得:
x=4
答:管塞同开的时间为4分钟
x+2x=3x(分钟)
x(分钟)
一元一次方程的应用
列方程解应用题的一般步骤是什么?
审——设——列——解——答(验)
注意事项:
1
在一道应用题中,往往含有几个未知数,应恰当的选择其中的一个,用x表示出来,然后根据数量之间的关系,将其他的几个未知量用含x的代数式表示出来。一般题目问什么,就设什么为x,但也会有例外;
2
方程两边要注意单位统一。
3
对于求得的解,还要看它是否符合实际意义,再写出答案
用一元一次方程分析和
解决实际问题的基本过程如下:
实际问题
数学问题
已知量,未知量,等量关系
一元一次方程
方程的解
解的合理性
实际问题答案
抽象
分析
列出
求出
验证
合理
1、甲、乙两地相距162公里,一列慢车从甲站开出,每小时走48公里,一列快车从乙站开出,每小时走60公里试问:
1)两列火车同时相向而行,多少时间可以相遇?
2)两车同时反向而行,几小时后两车相距270公里?
3)若两车相向而行,慢车先开出1小时,再用多少时间
两车才能相遇?
4)若两车相向而行,快车先开25分钟,快车开了几小时
与慢车相遇?
5)两车同时同向而行(快车在后面),几小时后快车
可以追上慢车?
6)两车同时同向而行(慢车在后面),几小时后两车相
距200公里?
一、相遇问题的基本题型
1、同时出发(两段)
二、相遇问题的等量关系
2、不同时出发
(三段
)
一、明确行程问题中三个量的关系
三个基本量关系是:速度×时间=路程
一、追及问题的基本题型
1、不同地点同时出发
二、追及问题的等量关系
2、同地点不同时出发
1、追及时快者行驶的路程-慢者行驶的路程=相距的
路程
2、追及时快者行驶的路程=慢者行驶的路程或
慢者所用时间=快者所用时间+多用时间
从甲地到乙地,水路比公路近40千米,上午十时,一艘轮船从甲地驶往乙地,下午1时一辆汽车从甲地驶往乙地,结果同时到达终点。已知轮船的速度是每小时24千米,汽车的速度是每小时40千米,求甲、乙两地水路、公路的长,以及汽车和轮船行驶的时间?
解:设水路长为x千米,则公路长为(x+40)千米
等量关系:船行时间-车行时间=3小时
答:水路长240千米,公路长为280千米,车行时间为
7小时,船行时间为10小时
依题意得:
x+40=280,
x=240
练习:1、两地相距28公里,小明以15公里/小时的速度。小亮以30公里/小时的速度,分别骑自行车和开汽车从同一地
前往另一地,小明先出发1小时,小亮几小时后才能
追上小明?
解:设小亮开车x
小时后才能追上小明,则小亮所行路
程为30x公里,小明所行路程为15(x+1)
等量关系:小亮所走路程=小明所走路程
依题意得:30x=15(x+1)
x=1
检验:两地相距28公里,在两地之间,小亮追不上小明
例题讲解:
例
汽船从甲地顺水开往乙地,所用时间比从乙地逆水
开往甲地少1.5小时。已知船在静水的速度为18千米/小时,
水流速度为2千米/小时,求甲、乙两地之间的距离?
分析:本题是行程问题,但涉及水流速度,必须要
掌握:顺水速度=船速+水速
逆水速度=船速-水速
解:(直接设元)
设甲、乙两地的距离为x
千米
等量关系:逆水所用时间-顺水所用时间=1.5
依题意得:
x=120
答:甲、乙两地的距离为120千米。
例
一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时。已知水流的速度是3千米/时,求船在静水中的速度。
分析:题中的等量关系为
这艘船往返的路程相等,即:
顺流速度×顺流时间=逆流速度×逆流时间
例
一艘船从甲码头到乙码头顺流行驶,用了2小时;从乙码头返回甲码头逆流行驶,用了2.5小时。已知水流的速度是3千米/时,求船在静水中的速度。
解:设船在静水中的平均速度为x千米/时,则顺流速度为(x+3)千米/时,逆流速度为(x-3)千米/时。
根据往返路程相等,列得
2(x+3)=2.5(x-3)
去括号,得
2x+6=2.5x-7.5
移项及合并,得
0.5x=13.5
X=27
答:船在静水中的平均速度为27千米/时。
练习:
1、一架飞机飞行两城之间,顺风时需要5小时30分钟,
逆风时需要6小时,已知风速为每小时24公里,
求两城之间的距离?
等量关系:顺风时飞机本身速度=逆风时飞机本身速度。
答:两城之间的距离为3168公里
注:飞行问题也是行程问题。同水流问题一样,飞行问
题的等量关系有:顺风飞行速度=飞机本身速度+风速
逆风飞行速度=飞机本身速度-风速
依题意得:
x=3168
解:设两城之间距离为x
公里,则顺风速为
公
里/小时,逆风速为
公里/小时
小结:
行程问题包括相遇、追击和飞行、航行的速度问题其基本关系是:路程=时间×速度
相遇问题的等量关系:甲行距离+乙行距离=总路程
追击问题的等量关系:
1)同时不同地
:
慢者行的距离+两者之间的距离=快者行的距离
2)同地不同时:
甲行距离=乙行距离
或
慢者所用时间=快者所用时间+多用时间
顺水逆水的问题的等量关系:
1)顺水的路程
=
逆水的路程
2)顺速
–
逆速
=
2水速;顺速
+
逆速
=
2船速
调配问题中的数量关系:
1.无论调配前后总量是否改变,调配后两量之间总有新的倍比关系,解这类题要注意分析调配后两个量之间的关系,从而找到等量关系。
2.关注调配前后总量的变化以及调配后两量之间出现的新的倍比关系,从而找到等量关系。
例5、
甲煤矿有煤432吨。乙煤矿有煤96吨,为了使甲煤矿存煤数是乙煤矿的2倍。应从甲煤矿运多少吨煤到乙煤矿?
分析:数量关系可用表来表示,看得更清楚,更直观。
原有煤量
调运煤量
调后存煤量
等量关系
煤
矿
甲
矿
乙
矿
涉及的量
432
96
-
x
+
x
432
-
x
96
+
x
调后甲矿存煤量=2×调后乙矿存煤量
解:设应从甲煤矿调运
x
吨煤到乙煤矿,那么调运后甲煤矿有煤(432-
x
)吨,
乙煤矿有煤(96
+
x
)吨,根据题意得:
432-x
=
2(96+x)
432-x
=
192+2x,
3x
=
240
X
=
80
答:应从甲煤矿调运80吨煤到乙煤矿。
、某部队开展支农活动,甲队27人,乙队19人,现另调26人去支援,使甲队是乙队的2倍,问应调往甲队、乙队各多少人?
解:设调往甲队x人,则调往乙队(26-x)人
根据题意,得方程:
解方程得:x
=
21
答:调往甲队21人。调往乙队5人。
练习2:甲槽有水34升,乙槽有水18升.现在两槽同时排水,都是平均每分排出2升.多少分钟后,甲槽的水是乙槽的水的3倍?
练习1:将全班45名同学分成两组植树,要求甲组每人挖5个坑,乙组每人挖3个坑并植7棵树,如何分配两组的人数,才能使挖的坑数与植树的棵数相等?
?
工程问题中的数量关系:
1)
工作效率=
工作总量
完成工作总量的时间
———————————
2)工作总量=工作效率×工作时间
3)工作时间=
工作总量
—————
工作效率
4)各队合作工作效率=各队工作效率之和
5)全部工作量之和=各队工作量之和
例题讲解
例1
挖一条长为1200米长的水渠,由甲施工队独做需要30
天完成,乙施工队独做需要20天完成,现在甲、乙两
施工队从两头同时施工,挖完这条水渠估计需几天?
等量关系:
甲施工队挖的米数+乙施工队挖的米数=1200米
答:两个施工队合作估计需要12天挖完。
解:设挖完这条水渠估计要x天.
依题意得
例2
修筑一条公路,甲工程队单独承包要80天完成,乙工程队单独
承包要120天完成
1)现在由两个工程队合作承包,几天可以完成?
2)如果甲、乙两工程队合作了30天后,因甲工作队另有任务,
剩下工作由乙工作队完成,则修好这条公路共需要几天?
解:
1)设两工程队合作需要x天完成。
2)设修好这条公路共需要
y
天完成。
等量关系:
甲30天工作量+乙队y天的工作量
=
1
答:两工程队合作需要48天完成,修好这条公路还需75天。
等量关系:甲工作量+乙工作量=1
依题意得
依题意得
y=75
x=48
等量关系:4天的工作量+改进后(x
–
4)工作量=
0.5
解:设一共x天可以修完它的一半。
依题意得
×4+
(x—4)=
0.5
答:一共
天可以修完它的一半。
例3
分析:
x=
例4
已知开管注水缸,10分钟可满,拨开底塞,满缸水20
分钟流完,现若管、塞同开,若干时间后,将底塞塞
住,又过了2倍的时间才注满水缸,求管塞同开的时
间是几分钟?
分析:
注入或放出率
注入或放出时间
注入或放出量
注入
放出
解:设两管同开x分钟
等量关系:注入量-放出量=缸的容量
依题意得:
x=4
答:管塞同开的时间为4分钟
x+2x=3x(分钟)
x(分钟)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
