1.1 二次函数课件 浙教版九年级数学上册(30张)
文档属性
| 名称 | 1.1 二次函数课件 浙教版九年级数学上册(30张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
浙教版数学教材九年级上册
第一章
二次函数
1.1
二次函数的图象和性质
1.1
二次函数
【学习目标】
1.理解掌握二次函数的概念,并且会判断函数是否是二次函数.
2.理解和掌握二次函数的一般形式.
3.会列二次函数表达式解决实际问题.
【学习重、难点】
重点:二次函数的概念和一般形式.
难点:会列二次函数表达式解决实际问题.
活动一
:【复习旧知
引出课题】
1.
我们已经学习了哪些函数?它们的图象是什么?
变量之间的关系
函数
一次函数
y=kx+b
(k≠0)
正比例函数y=kx
(k≠0)
它们的图象是一条直线.
2.出示图片:雨后天空的彩虹、拱桥的桥面上部结构、
公园里的喷泉、投篮等.
雨后天空的彩虹
桥面的上部结构
节日的喷泉给人带来喜庆,你是否注意过水流所经过的路线?它会与某种函数有联系吗?
奥运赛场腾空的篮球
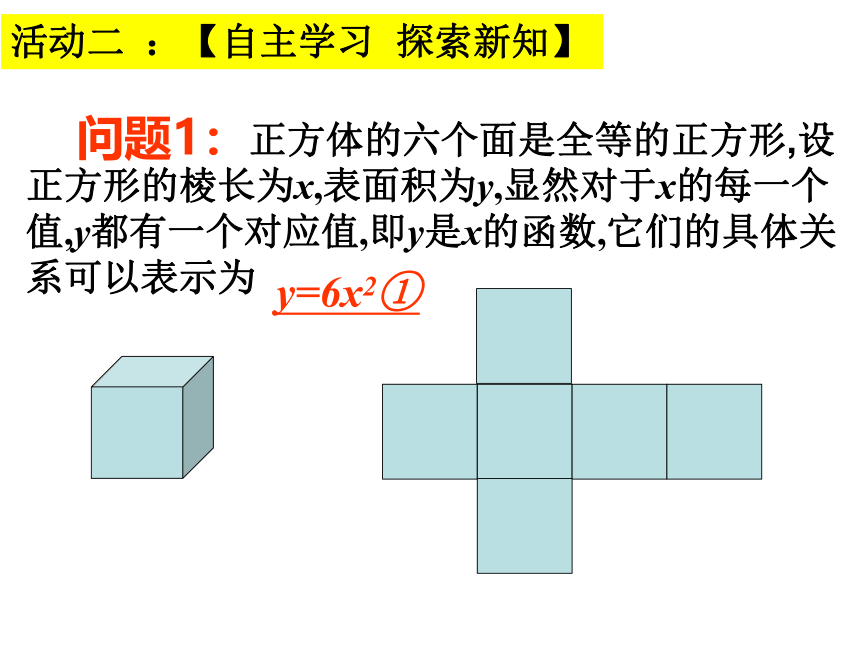
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
问题1:
y=6x2①
活动二
:【自主学习
探索新知】
多边形的对角线数d与边数n有什么关系?
问题2:
由图可以想出,如果多边形有n条边,那么它有
个顶点,从一个顶点出发,连接
与这点不相邻的各顶点,可以作
条
对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
即
②式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有唯一的对应值,即d是n的函数。
M
N
问题3
:某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
即
③
③式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
函数①②③有什么共同点?
观察:
y=6x2①
函数都是用
自变量的二次整式表示的
根据它们的共同特征,猜一猜可以怎么给它们命名?你用的什么方法?
二次函数
二次函数的定义:
形如y=ax?+bx+c(a,b,c是常数,a≠
0)的函数叫做二次函数.其中x是自变量,a,b,c分别是二次项系数、一次项系数和常数项.
温馨提示:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠
0;
(3)等式的右边最高次数为
2,可以没有一次项和常数项,但不能没有二次项.
归纳总结
二次函数的一般形式:
y=ax2+bx+c
(其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
活动三
:【运用新知
深化理解】
1、
说出下列二次函数的二次项系数、一次项系数、常数项.
(1)
y=-x2+58x-112
解:
二次项系数:
一次项系数:
常数项:
(2)y=πx2
解:
二次项系数:
一次项系数:
常数项:
-1
58
-112
π
0
0
2、指出下列函数y=ax?+bx+c中的a、b、c.
(1)
y=-3x2-x-1
解:a=-3,b=-1,c=-1
(2)
y=5x2-6
解:a=5,b=0,c=-6
(3)y=x(1+x)
解:a=1,b=1,c=0
注意:一定要化成y=ax?+bx+c
3.下列函数中哪些是二次函数?为什么?(x是自变量)
①
y=ax2+bx+c
②
s=3-2x?
③y=x2
④
⑤y=x?+x?+25
⑥
y=(x+3)?-x?
不一定是,缺少a≠0的条件.
不是,右边是分式.
不是,x的最高次数是3.
y=6x+9
m2—2m-1=2
m+1
≠0
∴m=3
∴当m=3时,该函数是二次函数.
例1:已知:函数y=
(m+1)x
+(m-3)x+m.
当m取何值时,它是二次函数?
解:由题意得
驶向胜利的彼岸
活动四
:【典例精讲
巩固提升】
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式如y=ax2,y=ax2+bx,
y=ax2+c等.
点
拨
例2:已知函数
(1)m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
第(2)问易忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案,需要引起同学们的重视.
点拨
一次函数y=kx+b
(k
≠0),其中包括正比例函数
y=kx(k≠0)
,
二次函数y=ax2+bx+c(a≠0).
现在我们学习过的函数有:
可以发现,这些函数的名称都形象地反映了函数表达式与自变量的关系.
归纳小结
1、已知函数
y=3x2m-1-5
①
当m=__时,y是关于x的一次函数;
②
当m=__时,y是关于x的二次函数
.
1
活动五:【学以致用】
2、若函数
是二次函数,求:
(1)求a的值.
(2)
求函数关系式.
(3)当x=-2时,y的值是多少?
解:
(1)由题意,得
解得
(2)当a=-1时,函数关系式为
.
(3)将x=-2代入函数关系式中,有
1.下列函数中,(x是自变量),是二次函数的有
。
A
、
y=ax2+bx+c
B
、
y2=x2-4x+1
C、
y=x2
D
、
y=2+
2.函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
A
m,n是常数,且m≠0
B
m,n是常数,且n≠0
C
m,n是常数,且m≠n
D
m,n为任何实数
C
C
活动五:【中考链接】
3.某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
解:由题意可得
-10x2+180x+400=1120,
整理得
x2-18x+72=0,
解得
x1=6,x2=12(舍去).
所以,该产品的质量档次为第6档.
【点拨】解决此类问题的关键是要吃透题意,确定变量,建立函数模型.
构建思维导图
二次函数
定
义
y=ax2+bx+c(a
≠0,a,b,c是常数)
一般形式
右边是整式;
自变量的指数是2;
二次项系数a
≠0.
特殊形式
y=ax2;
y=ax2+bx;
y=ax2+c(a
≠0,a,b,c是常数).
课堂小结
1、这节课,我学到了:
2、我还感到疑惑的是:
3、我的感悟或收获是:
1.教材练习;
2.《新课堂》第一课时.
作业布置
浙教版数学教材九年级上册
第一章
二次函数
1.1
二次函数的图象和性质
1.1
二次函数
【学习目标】
1.理解掌握二次函数的概念,并且会判断函数是否是二次函数.
2.理解和掌握二次函数的一般形式.
3.会列二次函数表达式解决实际问题.
【学习重、难点】
重点:二次函数的概念和一般形式.
难点:会列二次函数表达式解决实际问题.
活动一
:【复习旧知
引出课题】
1.
我们已经学习了哪些函数?它们的图象是什么?
变量之间的关系
函数
一次函数
y=kx+b
(k≠0)
正比例函数y=kx
(k≠0)
它们的图象是一条直线.
2.出示图片:雨后天空的彩虹、拱桥的桥面上部结构、
公园里的喷泉、投篮等.
雨后天空的彩虹
桥面的上部结构
节日的喷泉给人带来喜庆,你是否注意过水流所经过的路线?它会与某种函数有联系吗?
奥运赛场腾空的篮球
正方体的六个面是全等的正方形,设正方形的棱长为x,表面积为y,显然对于x的每一个值,y都有一个对应值,即y是x的函数,它们的具体关系可以表示为
问题1:
y=6x2①
活动二
:【自主学习
探索新知】
多边形的对角线数d与边数n有什么关系?
问题2:
由图可以想出,如果多边形有n条边,那么它有
个顶点,从一个顶点出发,连接
与这点不相邻的各顶点,可以作
条
对角线.
n
(n-3)
因为像线段MN与NM那样,连接相同两顶点的对角线是同一条对角线,所以多边形的对角线总数
即
②式表示了多边形的对角线数d与边数n之间的关系,对于n的每一个值,d都有唯一的对应值,即d是n的函数。
M
N
问题3
:某工厂一种产品现在的年产量是20件,计划今后两年增加产量.如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,y与x之间的关系应怎样表示?
即
③
③式表示了两年后的产量y与计划增产的倍数x之间的关系,对于x的每一个值,y都有一个对应值,即y是x的函数.
函数①②③有什么共同点?
观察:
y=6x2①
函数都是用
自变量的二次整式表示的
根据它们的共同特征,猜一猜可以怎么给它们命名?你用的什么方法?
二次函数
二次函数的定义:
形如y=ax?+bx+c(a,b,c是常数,a≠
0)的函数叫做二次函数.其中x是自变量,a,b,c分别是二次项系数、一次项系数和常数项.
温馨提示:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠
0;
(3)等式的右边最高次数为
2,可以没有一次项和常数项,但不能没有二次项.
归纳总结
二次函数的一般形式:
y=ax2+bx+c
(其中a、b、c是常数,a≠0)
二次函数的特殊形式:
当b=0时,
y=ax2+c
当c=0时,
y=ax2+bx
当b=0,c=0时,
y=ax2
活动三
:【运用新知
深化理解】
1、
说出下列二次函数的二次项系数、一次项系数、常数项.
(1)
y=-x2+58x-112
解:
二次项系数:
一次项系数:
常数项:
(2)y=πx2
解:
二次项系数:
一次项系数:
常数项:
-1
58
-112
π
0
0
2、指出下列函数y=ax?+bx+c中的a、b、c.
(1)
y=-3x2-x-1
解:a=-3,b=-1,c=-1
(2)
y=5x2-6
解:a=5,b=0,c=-6
(3)y=x(1+x)
解:a=1,b=1,c=0
注意:一定要化成y=ax?+bx+c
3.下列函数中哪些是二次函数?为什么?(x是自变量)
①
y=ax2+bx+c
②
s=3-2x?
③y=x2
④
⑤y=x?+x?+25
⑥
y=(x+3)?-x?
不一定是,缺少a≠0的条件.
不是,右边是分式.
不是,x的最高次数是3.
y=6x+9
m2—2m-1=2
m+1
≠0
∴m=3
∴当m=3时,该函数是二次函数.
例1:已知:函数y=
(m+1)x
+(m-3)x+m.
当m取何值时,它是二次函数?
解:由题意得
驶向胜利的彼岸
活动四
:【典例精讲
巩固提升】
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式如y=ax2,y=ax2+bx,
y=ax2+c等.
点
拨
例2:已知函数
(1)m取什么值时,此函数是正比例函数?
(2)
m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
第(2)问易忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案,需要引起同学们的重视.
点拨
一次函数y=kx+b
(k
≠0),其中包括正比例函数
y=kx(k≠0)
,
二次函数y=ax2+bx+c(a≠0).
现在我们学习过的函数有:
可以发现,这些函数的名称都形象地反映了函数表达式与自变量的关系.
归纳小结
1、已知函数
y=3x2m-1-5
①
当m=__时,y是关于x的一次函数;
②
当m=__时,y是关于x的二次函数
.
1
活动五:【学以致用】
2、若函数
是二次函数,求:
(1)求a的值.
(2)
求函数关系式.
(3)当x=-2时,y的值是多少?
解:
(1)由题意,得
解得
(2)当a=-1时,函数关系式为
.
(3)将x=-2代入函数关系式中,有
1.下列函数中,(x是自变量),是二次函数的有
。
A
、
y=ax2+bx+c
B
、
y2=x2-4x+1
C、
y=x2
D
、
y=2+
2.函数
y=(m-n)x2+
mx+n
是二次函数的条件是(
)
A
m,n是常数,且m≠0
B
m,n是常数,且n≠0
C
m,n是常数,且m≠n
D
m,n为任何实数
C
C
活动五:【中考链接】
3.某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
解:由题意可得
-10x2+180x+400=1120,
整理得
x2-18x+72=0,
解得
x1=6,x2=12(舍去).
所以,该产品的质量档次为第6档.
【点拨】解决此类问题的关键是要吃透题意,确定变量,建立函数模型.
构建思维导图
二次函数
定
义
y=ax2+bx+c(a
≠0,a,b,c是常数)
一般形式
右边是整式;
自变量的指数是2;
二次项系数a
≠0.
特殊形式
y=ax2;
y=ax2+bx;
y=ax2+c(a
≠0,a,b,c是常数).
课堂小结
1、这节课,我学到了:
2、我还感到疑惑的是:
3、我的感悟或收获是:
1.教材练习;
2.《新课堂》第一课时.
作业布置
同课章节目录
