第5章 一次函数课题学习 怎样选择较优方案 课件 浙教版七年级数学上册(17张)
文档属性
| 名称 | 第5章 一次函数课题学习 怎样选择较优方案 课件 浙教版七年级数学上册(17张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 221.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
课题学习---怎样选择最优方案
怎样租车
学习目标:
1.会用一次函数知识解决方案选择问题,体会函数模型思想;
2.能从不同的角度思考问题,优化解决问题的方法;
3.认识数学在现实生活中的意义,发展运用数学知识解决实际问题的能力.
为了贯彻落实市委市府提出的“精准扶贫”精神.某公司制定了一系列帮扶计划.其中一项计划是将330台农用机器一次性运送到某地,计划租用甲、乙两种货车.已知每辆甲种货车一次最多运送机器65台、租车费用为500元,每辆乙种货车一次最多运送机器45台、租车费用为350元.
(1)需要租多少台车?(最少需要租多少台车,最多呢?)
(2)在最少租用台数的前提下共有哪几种租车方案?
快乐热身
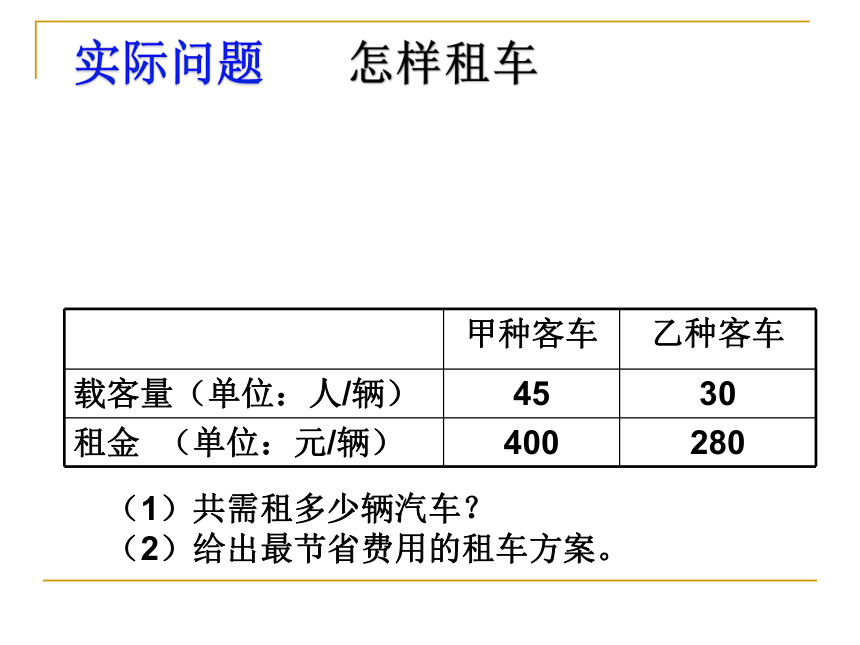
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案。
实际问题
怎样租车
(2)由题意可知共有6名教师,要使每辆汽车上至少要有1名教师,汽车总数不能大于
辆。
综合(
1
)(2)可知汽车总数为
辆。
6
8
6
(1)由上表可知甲乙两车最多载客量为:甲车45人,乙车30人,要保证240名师生有车坐,则只租甲车需
辆,只租乙车需
辆。所以租用汽车的总数可以为
。
6
6,7,8
(3)根据已知条件,能否只租甲种客车,为什么?那该怎么办?
分析问题
二、
若设租用x辆甲种客车,则租用乙种客车(6-x)辆。
(2)甲车有x辆,每辆车需租金400元,则共需
元。乙车有(6-x)辆,每辆车需租金280元,则共需
元。为使租车费用不超过2300元,则可列不等式为
。
(
1
)甲车有x辆,每辆可载客45人,则共可载
人。乙车有(6-x)辆,每辆可载客30人,则共可载
人。为使240名师生有车坐,则可列不等式为
。
45x+30(6-x)≥240
400x+280(6-x)
≤2300
400x
45x
30(6-x)
280(6-x)
(3)综合(
1
)
(2)中不等式得
45x+30(6-x)≥240
400x+280(6-x)
≤2300
(4)不等式组的解集为
。其中x表示甲车的车辆数,所以x
的取值可以为____
。
4
或
5
4≤x≤
讨论问题
4辆甲种客车,2辆乙种客车;
5辆甲种客车,1辆乙种客车;
y1=400×4+280×2=2160<2300
y2=
400×5+280×1=2280<2300
答:应租用
4辆甲种客车,2辆乙种客车比较节省费用。
方案一
方案二
2280-2160
=
120
y1通过刚才的分析,你能得出哪几种不同的租车方案?
解决问题
为了贯彻落实市委市府提出的“精准扶贫”精神.某公司制定了一系列帮扶计划.其中一项计划是将330台农用机器一次性运送到某地,计划租用甲、乙两种货车.已知每辆甲种货车一次最多运送机器65台、租车费用为500元,每辆乙种货车一次最多运送机器45台、租车费用为350元.
(1)需要租多少台车?(最少需要租多少台车,最多呢?)
(2)在最少租用台数的前提下共有哪几种租车方案?
(3)在最少租用台数的前提下哪种租车方案费用最少。
课堂小结
实际问题
函数模型
实际问题的解
函数模型的解
抽象概括
还原说明
(某公司计划生产M、N两种型号时装共80套。
M型号时装
N型号时装
需要原料
A布料:0.6米
B布料:0.9米
A布料:1.1米
B布料:0.4米
每套获利
45元
50元
设生产
N型号
时装套数为x,公司生产两种型号的时装获得的总利润为y元。
(1)求总利润y与x的函数关系式。
(2)现在公司共有A种布料70m,B种布料52m。求x的范围。
(3)该公司计划生产N型号的时装多少套时,获得的利润最大?最大利润是多少?
。
课后作业
自2008年6月1日起,我国实行“限塑令”,开始有偿使用环保购物袋。为满足市场需求,某厂家生产A、B
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋成本及售价如右表:
设每天生产的A种购物袋有x个,每天获得的总利润为
y元。
练一练
成本(元/个)
售价(元/个)
A
2
2.3
B
3
3.5
(1)请写出每天的总利润y与x的函数关系式。
(2)若该厂每天最多能投入的成本是1万元,那么每天企业最多能获利多少
解:(1)若每天生产的A种购物袋有x个,则B种购
物袋有
4500-x
个,由题意得:
每天的总利润:y=(2.3-2)x+(3.5-3)(4500-x)
化简得:y=2250-0.2x,0≤x
≤4500
(2)每天的总成本为:2x+3×(4500-x)=13500-x
根据题意:13500-x
≤10000
x
≥3500
若每天投入的成本不超过1万元,则:3500≤x
≤4500
每天的总利润为y=2250-0.2x,当x最小时,y值最大。
x=3500时,y=1550
该厂每天生产3500个A种购物袋时,能获得最大利润
1550元。
(1)练习:导读与训练70页第3题
联系与想象
(2)(常州中考题)向阳花卉基地出售两种鲜花:百合与玫瑰,其中,玫瑰4元/株,百合5元/株。如果客户一次性购买
玫瑰的数量大于1200株,那么每株玫瑰可以降价1元。
某鲜花店向花卉基地采购了玫瑰1000株~1500株,百合若干株,并恰好花去了9000元。然后又以玫瑰5元,百合6.3元的价格将鲜花卖出。问:如果花店获得的毛利润最大,你知道采购的玫瑰和百合的数量分别是多少吗?
(注:毛利润=鲜花店卖出百合和玫瑰所获的总费用-购进百合和玫瑰的所需的总费用.)
玫瑰1500株,百合900株,毛利润4350元
4辆甲种客车,2辆乙种客车;
5辆甲种客车,1辆乙种客车;
y1=120×4+1680=2160
y2=120×5+1680=2280
应选择方案一,它比方案二节约120元。
方案一
方案二
公司共有A种布料70m,B种布料52m。
生产中总共使用的A布料不能超过70m
总共使用的B布料不能超过52m
分析
1.1x+0.6(80-x)
≤70
0.5x+48≤70
0.4x+0.9(80-x)
≤52
72-0.5x≤52
40
≤
x
≤
44
总共生产80套:0
≤x
≤80
生产N型号的时装多少套,获得的利润最大
也就是说:求x为多少时,y值最大
分析
N型号时装的套数为x,公司获得的总利润为y元
y=5x+3600
40
≤
x
≤
44
当x=44时,y值最大,y=3820。
也就是说,该公司生产M型时装36套,N型时装44套时,获得的总利润最大,为3820元。
当x取最大值时,y值最大。
马上下课
课题学习---怎样选择最优方案
怎样租车
学习目标:
1.会用一次函数知识解决方案选择问题,体会函数模型思想;
2.能从不同的角度思考问题,优化解决问题的方法;
3.认识数学在现实生活中的意义,发展运用数学知识解决实际问题的能力.
为了贯彻落实市委市府提出的“精准扶贫”精神.某公司制定了一系列帮扶计划.其中一项计划是将330台农用机器一次性运送到某地,计划租用甲、乙两种货车.已知每辆甲种货车一次最多运送机器65台、租车费用为500元,每辆乙种货车一次最多运送机器45台、租车费用为350元.
(1)需要租多少台车?(最少需要租多少台车,最多呢?)
(2)在最少租用台数的前提下共有哪几种租车方案?
快乐热身
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案。
实际问题
怎样租车
(2)由题意可知共有6名教师,要使每辆汽车上至少要有1名教师,汽车总数不能大于
辆。
综合(
1
)(2)可知汽车总数为
辆。
6
8
6
(1)由上表可知甲乙两车最多载客量为:甲车45人,乙车30人,要保证240名师生有车坐,则只租甲车需
辆,只租乙车需
辆。所以租用汽车的总数可以为
。
6
6,7,8
(3)根据已知条件,能否只租甲种客车,为什么?那该怎么办?
分析问题
二、
若设租用x辆甲种客车,则租用乙种客车(6-x)辆。
(2)甲车有x辆,每辆车需租金400元,则共需
元。乙车有(6-x)辆,每辆车需租金280元,则共需
元。为使租车费用不超过2300元,则可列不等式为
。
(
1
)甲车有x辆,每辆可载客45人,则共可载
人。乙车有(6-x)辆,每辆可载客30人,则共可载
人。为使240名师生有车坐,则可列不等式为
。
45x+30(6-x)≥240
400x+280(6-x)
≤2300
400x
45x
30(6-x)
280(6-x)
(3)综合(
1
)
(2)中不等式得
45x+30(6-x)≥240
400x+280(6-x)
≤2300
(4)不等式组的解集为
。其中x表示甲车的车辆数,所以x
的取值可以为____
。
4
或
5
4≤x≤
讨论问题
4辆甲种客车,2辆乙种客车;
5辆甲种客车,1辆乙种客车;
y1=400×4+280×2=2160<2300
y2=
400×5+280×1=2280<2300
答:应租用
4辆甲种客车,2辆乙种客车比较节省费用。
方案一
方案二
2280-2160
=
120
y1
解决问题
为了贯彻落实市委市府提出的“精准扶贫”精神.某公司制定了一系列帮扶计划.其中一项计划是将330台农用机器一次性运送到某地,计划租用甲、乙两种货车.已知每辆甲种货车一次最多运送机器65台、租车费用为500元,每辆乙种货车一次最多运送机器45台、租车费用为350元.
(1)需要租多少台车?(最少需要租多少台车,最多呢?)
(2)在最少租用台数的前提下共有哪几种租车方案?
(3)在最少租用台数的前提下哪种租车方案费用最少。
课堂小结
实际问题
函数模型
实际问题的解
函数模型的解
抽象概括
还原说明
(某公司计划生产M、N两种型号时装共80套。
M型号时装
N型号时装
需要原料
A布料:0.6米
B布料:0.9米
A布料:1.1米
B布料:0.4米
每套获利
45元
50元
设生产
N型号
时装套数为x,公司生产两种型号的时装获得的总利润为y元。
(1)求总利润y与x的函数关系式。
(2)现在公司共有A种布料70m,B种布料52m。求x的范围。
(3)该公司计划生产N型号的时装多少套时,获得的利润最大?最大利润是多少?
。
课后作业
自2008年6月1日起,我国实行“限塑令”,开始有偿使用环保购物袋。为满足市场需求,某厂家生产A、B
两种款式的布质环保购物袋,每天共生产4500个,两种购物袋成本及售价如右表:
设每天生产的A种购物袋有x个,每天获得的总利润为
y元。
练一练
成本(元/个)
售价(元/个)
A
2
2.3
B
3
3.5
(1)请写出每天的总利润y与x的函数关系式。
(2)若该厂每天最多能投入的成本是1万元,那么每天企业最多能获利多少
解:(1)若每天生产的A种购物袋有x个,则B种购
物袋有
4500-x
个,由题意得:
每天的总利润:y=(2.3-2)x+(3.5-3)(4500-x)
化简得:y=2250-0.2x,0≤x
≤4500
(2)每天的总成本为:2x+3×(4500-x)=13500-x
根据题意:13500-x
≤10000
x
≥3500
若每天投入的成本不超过1万元,则:3500≤x
≤4500
每天的总利润为y=2250-0.2x,当x最小时,y值最大。
x=3500时,y=1550
该厂每天生产3500个A种购物袋时,能获得最大利润
1550元。
(1)练习:导读与训练70页第3题
联系与想象
(2)(常州中考题)向阳花卉基地出售两种鲜花:百合与玫瑰,其中,玫瑰4元/株,百合5元/株。如果客户一次性购买
玫瑰的数量大于1200株,那么每株玫瑰可以降价1元。
某鲜花店向花卉基地采购了玫瑰1000株~1500株,百合若干株,并恰好花去了9000元。然后又以玫瑰5元,百合6.3元的价格将鲜花卖出。问:如果花店获得的毛利润最大,你知道采购的玫瑰和百合的数量分别是多少吗?
(注:毛利润=鲜花店卖出百合和玫瑰所获的总费用-购进百合和玫瑰的所需的总费用.)
玫瑰1500株,百合900株,毛利润4350元
4辆甲种客车,2辆乙种客车;
5辆甲种客车,1辆乙种客车;
y1=120×4+1680=2160
y2=120×5+1680=2280
应选择方案一,它比方案二节约120元。
方案一
方案二
公司共有A种布料70m,B种布料52m。
生产中总共使用的A布料不能超过70m
总共使用的B布料不能超过52m
分析
1.1x+0.6(80-x)
≤70
0.5x+48≤70
0.4x+0.9(80-x)
≤52
72-0.5x≤52
40
≤
x
≤
44
总共生产80套:0
≤x
≤80
生产N型号的时装多少套,获得的利润最大
也就是说:求x为多少时,y值最大
分析
N型号时装的套数为x,公司获得的总利润为y元
y=5x+3600
40
≤
x
≤
44
当x=44时,y值最大,y=3820。
也就是说,该公司生产M型时装36套,N型时装44套时,获得的总利润最大,为3820元。
当x取最大值时,y值最大。
马上下课
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
