6.8 余角和补角课件 浙教版七年级数学上册(18张)
文档属性
| 名称 | 6.8 余角和补角课件 浙教版七年级数学上册(18张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 644.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
6.8余角和补角
思考问题:∠1与∠2之间的角度有什么关系?
如果两个角的和是直角,那么这两个角
一长方形纸片,按如图所示沿虚线折叠,
并标出∠1与∠2
,∠3与∠4.
∠1
+
∠2
=
90
°
互为余角。
简称互余,也可以说其中一个角是另一个角的余角。
数学符号表示:
1
2
4
3
思考问题:∠3与∠4之间的角度有什么关系?
如果两个角的和是平角,那么这两个角
准备一长方形纸片,按如图所示沿虚线折叠,
并标出∠1与∠2
,∠3与∠4.
∠3+
∠4
=
180
°
互为补角。
简称互补,也可以说其中一个角是另一个角的补角。
数学符号表示:
1
2
4
3
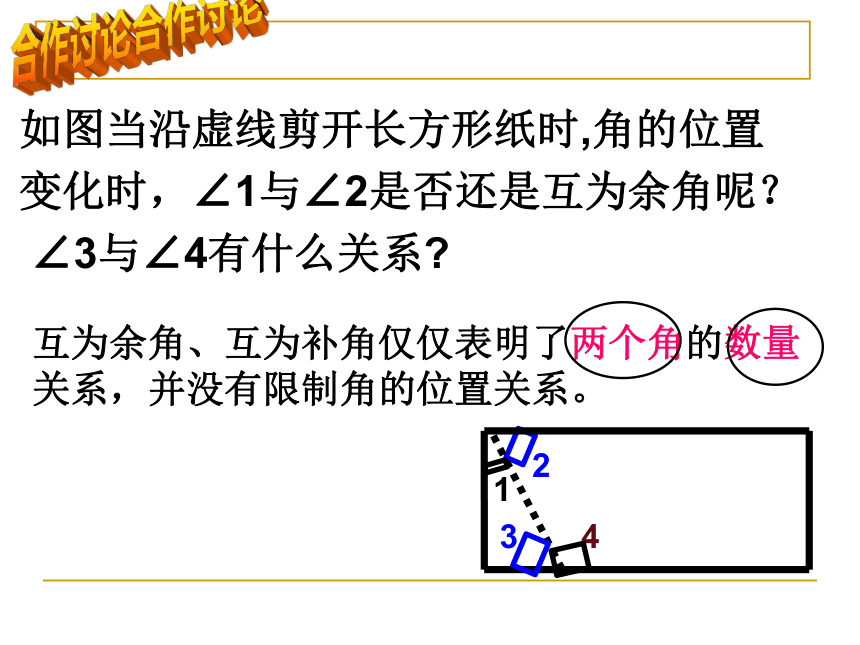
如图当沿虚线剪开长方形纸时,角的位置
变化时,∠1与∠2是否还是互为余角呢?
∠3与∠4有什么关系?
互为余角、互为补角仅仅表明了两个角的数量关系,并没有限制角的位置关系。
1
2
4
3
做一做
(1)∵
∠
1+
∠
3=
42°+
48°=90°
∴
∠
1与
∠
3互余.
如图,已经∠
1=42°,
∠
2=138°,
∠
3=48°问图中有互余或互补的角?
若有,请把它们写出来,并说明理由。
1
2
3
(2)∵
∠
1+
∠
2=
42°+
138°=180°
∴
∠
1与
∠
2互补.
1、判断题:
(1)
?
1=90°,那么它是余角。
(
)
(2)如果
,
则?
1
,?
2,?
3
互为补角.(
)
(3)互余的两个角必定都是锐角。
(
)
(4)一个角的补角必定是钝角。
(
)
?
?
?
?
∠α
∠α的余角
∠α的补角
5°
85°
175°
77°
13°
103°
62°23′
27°37′
117°37′
x
90-x
180-x
从上表中你发现∠α的补角与∠α的余角的度数有什么关系吗?你能说明理由吗?
1、若?
1与?
2互补,则?
1+
?2=____
2、30°的余角是_____,补角是____
3、若?
?=60°32′,则?
?的余角是
____,
?
?的补角是_________,
若一个角的度数是x°,则它的余角的度数
是
;补角的度数是_________
4、60°的余角的补角是___________
180°
60°
150°
29°28′
119°28′
(90-x)°
150°
(180-x)°
如图,O是直线AB上的一点,OC是?
AOB的角平分线。
看图回答:
1、图中互余的角是___________________
2、图中互补的角是______________________
3、图中相等的角是
______________________
A
B
O
C
D
?
AOD与?
DOC
?
AOD与?
DOB,?
AOC与?
BOC
?
AOC与?
BOC
变式:如右图,在上题的基础上添加一条射线OE,使得?
DOE是一个直角,回答下列问题:
图中?
DOC的余角有
___________________
图中?
AOD的余角有
___________________
(3)
通过上述两小题你能得到什么结论?
?
AOD与?COE
?
DOC与?BOE
同
角 的
余
角
相
等。
(等角)
如此图中,
∵
?
AOD
+
?
COD
=90°
,
?
COE
+
?
COD
=
90°,
∴
?
AOD=
?
COE
A
B
O
C
D
E
(4)
?
AOD的补角是___________
?
BOD
A
B
O
C
D
E
(5)
图中有与?
COE互补的角吗?________
?
BOD
(6)
通过此题,你又能得到什么结论?
同
角
的
补
角
相
等。
(等角)
例1:如图.已知∠AOC=
∠BOD=90°
指出图中还有哪些角相等,并说明理由.
O
D
C
B
A
E
Q:若将射线OA反向延长至E,其它条件保持不变,图中有哪些角互余?并说明理由。
两个概念
互余的角
互补的角
数量关系
性质
对应图形
C
D
E
N
A
O
B
M
?1+
?2=90°
?1+
?2=180°
同角(等角)的余角相等
同角(等角)的补角相等
已知一个角的补角是这个角的余角
的4倍,求这个角的度数.
例2
解:设这个角的度数为
,则依题意得
答:这个角的余角的度数为
另解:设这个角的余角的度数为
,
则它的补角可设为
答:这个角的余角的度数为
1.已知∠1=40°,求∠1的余角是多少?
2.已知∠1=∠2,∠1=40°,则∠2的余角是多少呢?
3.若一个角的补角和这个角的余角互补,
求这个角.
试一试
看谁思考的快!!
1.锐角的余角一定是锐角吗?
2.一个锐角和一个钝角一定互为补角吗?
3.一个角的补角比这个角的余角大多少度?
4.相等且互补的两个角各是多少度?
5.一个角的补角一定比这个角大吗?
6.只有锐角有余角
一定
(不一定)
(大90°)
(90°、
90°)
(不一定)
(正确)
探究活动:
如图:射线OA表示北偏西
(一般不说成
“西偏北
”方向,你能用类似的方法画图
表示下列各方向吗?
(1)北偏东
(2)南偏西
(一般不说成”西偏南
”)
(3)西南方向(即南偏西
)
B
C
40°
50°
D
探究活动:
B
C
40°
50°
D
1.表示(1),(2)方向的两条射线所成的角是多少度?
2.表示(2),(3)方向的两条射线所成的角是多少度?
3.在日常生活中,我们什么时候会用到这样的表示方法?
6.8余角和补角
思考问题:∠1与∠2之间的角度有什么关系?
如果两个角的和是直角,那么这两个角
一长方形纸片,按如图所示沿虚线折叠,
并标出∠1与∠2
,∠3与∠4.
∠1
+
∠2
=
90
°
互为余角。
简称互余,也可以说其中一个角是另一个角的余角。
数学符号表示:
1
2
4
3
思考问题:∠3与∠4之间的角度有什么关系?
如果两个角的和是平角,那么这两个角
准备一长方形纸片,按如图所示沿虚线折叠,
并标出∠1与∠2
,∠3与∠4.
∠3+
∠4
=
180
°
互为补角。
简称互补,也可以说其中一个角是另一个角的补角。
数学符号表示:
1
2
4
3
如图当沿虚线剪开长方形纸时,角的位置
变化时,∠1与∠2是否还是互为余角呢?
∠3与∠4有什么关系?
互为余角、互为补角仅仅表明了两个角的数量关系,并没有限制角的位置关系。
1
2
4
3
做一做
(1)∵
∠
1+
∠
3=
42°+
48°=90°
∴
∠
1与
∠
3互余.
如图,已经∠
1=42°,
∠
2=138°,
∠
3=48°问图中有互余或互补的角?
若有,请把它们写出来,并说明理由。
1
2
3
(2)∵
∠
1+
∠
2=
42°+
138°=180°
∴
∠
1与
∠
2互补.
1、判断题:
(1)
?
1=90°,那么它是余角。
(
)
(2)如果
,
则?
1
,?
2,?
3
互为补角.(
)
(3)互余的两个角必定都是锐角。
(
)
(4)一个角的补角必定是钝角。
(
)
?
?
?
?
∠α
∠α的余角
∠α的补角
5°
85°
175°
77°
13°
103°
62°23′
27°37′
117°37′
x
90-x
180-x
从上表中你发现∠α的补角与∠α的余角的度数有什么关系吗?你能说明理由吗?
1、若?
1与?
2互补,则?
1+
?2=____
2、30°的余角是_____,补角是____
3、若?
?=60°32′,则?
?的余角是
____,
?
?的补角是_________,
若一个角的度数是x°,则它的余角的度数
是
;补角的度数是_________
4、60°的余角的补角是___________
180°
60°
150°
29°28′
119°28′
(90-x)°
150°
(180-x)°
如图,O是直线AB上的一点,OC是?
AOB的角平分线。
看图回答:
1、图中互余的角是___________________
2、图中互补的角是______________________
3、图中相等的角是
______________________
A
B
O
C
D
?
AOD与?
DOC
?
AOD与?
DOB,?
AOC与?
BOC
?
AOC与?
BOC
变式:如右图,在上题的基础上添加一条射线OE,使得?
DOE是一个直角,回答下列问题:
图中?
DOC的余角有
___________________
图中?
AOD的余角有
___________________
(3)
通过上述两小题你能得到什么结论?
?
AOD与?COE
?
DOC与?BOE
同
角 的
余
角
相
等。
(等角)
如此图中,
∵
?
AOD
+
?
COD
=90°
,
?
COE
+
?
COD
=
90°,
∴
?
AOD=
?
COE
A
B
O
C
D
E
(4)
?
AOD的补角是___________
?
BOD
A
B
O
C
D
E
(5)
图中有与?
COE互补的角吗?________
?
BOD
(6)
通过此题,你又能得到什么结论?
同
角
的
补
角
相
等。
(等角)
例1:如图.已知∠AOC=
∠BOD=90°
指出图中还有哪些角相等,并说明理由.
O
D
C
B
A
E
Q:若将射线OA反向延长至E,其它条件保持不变,图中有哪些角互余?并说明理由。
两个概念
互余的角
互补的角
数量关系
性质
对应图形
C
D
E
N
A
O
B
M
?1+
?2=90°
?1+
?2=180°
同角(等角)的余角相等
同角(等角)的补角相等
已知一个角的补角是这个角的余角
的4倍,求这个角的度数.
例2
解:设这个角的度数为
,则依题意得
答:这个角的余角的度数为
另解:设这个角的余角的度数为
,
则它的补角可设为
答:这个角的余角的度数为
1.已知∠1=40°,求∠1的余角是多少?
2.已知∠1=∠2,∠1=40°,则∠2的余角是多少呢?
3.若一个角的补角和这个角的余角互补,
求这个角.
试一试
看谁思考的快!!
1.锐角的余角一定是锐角吗?
2.一个锐角和一个钝角一定互为补角吗?
3.一个角的补角比这个角的余角大多少度?
4.相等且互补的两个角各是多少度?
5.一个角的补角一定比这个角大吗?
6.只有锐角有余角
一定
(不一定)
(大90°)
(90°、
90°)
(不一定)
(正确)
探究活动:
如图:射线OA表示北偏西
(一般不说成
“西偏北
”方向,你能用类似的方法画图
表示下列各方向吗?
(1)北偏东
(2)南偏西
(一般不说成”西偏南
”)
(3)西南方向(即南偏西
)
B
C
40°
50°
D
探究活动:
B
C
40°
50°
D
1.表示(1),(2)方向的两条射线所成的角是多少度?
2.表示(2),(3)方向的两条射线所成的角是多少度?
3.在日常生活中,我们什么时候会用到这样的表示方法?
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
