2021-2022学年浙教版九年级数学上册4.1 比例线段课件(22张)
文档属性
| 名称 | 2021-2022学年浙教版九年级数学上册4.1 比例线段课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第四章
相似三角形
小组合作(时间6分钟)
请组长带领组员梳理我们预习中碰到的疑问,并做好记录。
这个比例式有何特别之处?
1.已知数a=4,c=9,若a:b=b:c,求b的值。
2.已知线段a=4,c=9,若a:b=b:c,求b的值。
概念:
概念辨析:
9
1
A
B
C
D
F
E
著名画家达?芬奇的名画<蒙娜丽莎>,画中脸部被围在矩形ABCD中,图中四边形BCEF为正方形,而在线段AB上的点F把线段AB分成两条线段AF、BF,其中
AB
BF
BF
AF
=
.
.
.
A
P
B
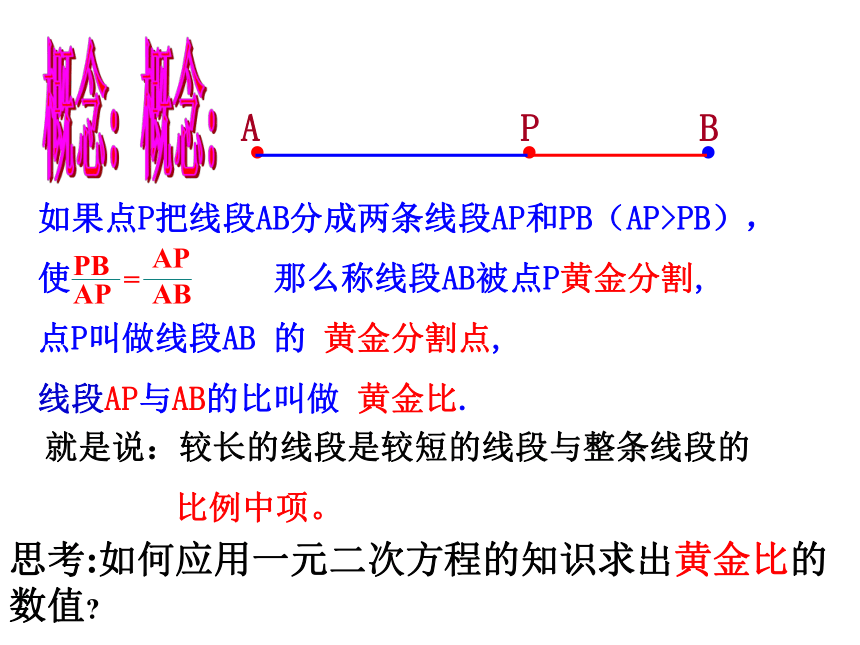
如果点P把线段AB分成两条线段AP和PB(AP>PB),
使
那么称线段AB被点P黄金分割,
点P叫做线段AB
的
黄金分割点,
线段AP与AB的比叫做
黄金比.
PB
AP
AP
AB
=
思考:如何应用一元二次方程的知识求出黄金比的数值?
就是说:较长的线段是较短的线段与整条线段的
比例中项。
B
P
A
实际应用
1.写作业时,要想使写出来的作业看起
来美观,写字大小约占格子的(
)
(A)
(B)
(C)
(D)
3
1
2
1
3
2
4
3
D
2.在人体下半身与身高的比例上,越接近0.618,越给人美感,遗憾的是,即使是身体修长的芭蕾舞演员也达不到如此的完美。某女士身高1.68米,下半身1.02米,她应该选择多高的高跟鞋看起来更美呢?
(只要求列式)
追溯黄金分割的历史文化
早在古希腊,数学家、天文学家欧多克索斯(Eudoxus,约前400——前347)曾提出:能否将一条线段分成不相等的两部分,使较短线段与较长线段的比等于较长线段与原线段的比?这就是黄金分割问题.
她的上半
身和下半身的比值接近
0.618.
世界艺术珍品——维纳斯女神
,她是西元前一
百多年希腊雕塑鼎盛时
期的代表作,
黄金分割原理最初运用于雕塑和建筑
数学美的魅力
1
古埃及胡夫金字塔
古希腊巴特农神庙
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边
长与高之比都接近于0.618.
古希腊的一些神庙,在建筑时高和宽也是按黄金比0.618来建立,他们认为这样的长方形看来是较美观;其大理石柱廓,就是根据黄金分割律分割整个神庙的.
你知道芭蕾舞演员跳舞时为什么要掂起脚尖吗?
芭蕾舞演员的身段是苗条的,但下半身与身高的比值也只有0.58左右,演员在表演时掂起脚尖,身高就可以增加6-8cm.这时比值就接近0.618了,给人以更为优美的艺术形象.
芭蕾舞
观察
欣赏
黄金分割
与生活
由黄金分割画出的正五角星形,有庄严雄健之美.
A
B
P
上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?
468m
?
实际应用
468×0.618≈289.2m
作法:
(1)过已知线段AB的端点B作BC⊥AB
使
例:已知线段AB=a,用直尺和圆规作出它的黄金分割点。
(2)连接AC,在CA上截取CD=CB
(3)在AB上截取AP=AD
问:点P是线段AB唯一的黄金分割点吗
A
B
C
D
P
A
B
a
如图所示,把窗台看成线段AB,点P是
AB的黄金分割点,AP>PB,求
(1)
(2)若AB=2米,则AP=_______米,
PB
=_______米
练习:
A
B
P
把窗台看成线段AB,现把原放置在窗台上点A处的一盆花,移到该线段的黄金分割点上,若AB=2米,试计算这盆花移动后应离A点几米?
变式练习
A
B
C
D
两花盆C、D之间有多远?
课堂小结
通过这节课的学习,你在知识上,方法上都有哪些收获?
1、什么是比例中项。
2、什么是黄金分割。
3、如何去确定黄金分割点或黄金比。
4、要用数学美去装点和美化生活。
如图,设AB是已知线段,以AB为边作正方形ABCD,取AD的中点E,连结EB,延长DA至点F,使EF=EB。以线段AF为边作正方形AFGH,则点H是线段AB的黄金分割点,你能说出这种方法的道理吗?
A
B
C
D
E
F
G
H
1.作顶角为36°的等腰△ABC;量出
底BC与腰AB的长度,计算:
;
2.作∠B的平分线,交AC于点D,量出CD的长度,
再计算:
.
(精确到0.001)
D
C
A
B
E
尝试
0.618
0.618
☆再作∠C的平分线,交BD于E,
△CDE也是黄金三角形……
D
☆顶角为36°的等腰三角形称为
黄金三角形
☆点D是线段AC的黄金分割点.
第四章
相似三角形
小组合作(时间6分钟)
请组长带领组员梳理我们预习中碰到的疑问,并做好记录。
这个比例式有何特别之处?
1.已知数a=4,c=9,若a:b=b:c,求b的值。
2.已知线段a=4,c=9,若a:b=b:c,求b的值。
概念:
概念辨析:
9
1
A
B
C
D
F
E
著名画家达?芬奇的名画<蒙娜丽莎>,画中脸部被围在矩形ABCD中,图中四边形BCEF为正方形,而在线段AB上的点F把线段AB分成两条线段AF、BF,其中
AB
BF
BF
AF
=
.
.
.
A
P
B
如果点P把线段AB分成两条线段AP和PB(AP>PB),
使
那么称线段AB被点P黄金分割,
点P叫做线段AB
的
黄金分割点,
线段AP与AB的比叫做
黄金比.
PB
AP
AP
AB
=
思考:如何应用一元二次方程的知识求出黄金比的数值?
就是说:较长的线段是较短的线段与整条线段的
比例中项。
B
P
A
实际应用
1.写作业时,要想使写出来的作业看起
来美观,写字大小约占格子的(
)
(A)
(B)
(C)
(D)
3
1
2
1
3
2
4
3
D
2.在人体下半身与身高的比例上,越接近0.618,越给人美感,遗憾的是,即使是身体修长的芭蕾舞演员也达不到如此的完美。某女士身高1.68米,下半身1.02米,她应该选择多高的高跟鞋看起来更美呢?
(只要求列式)
追溯黄金分割的历史文化
早在古希腊,数学家、天文学家欧多克索斯(Eudoxus,约前400——前347)曾提出:能否将一条线段分成不相等的两部分,使较短线段与较长线段的比等于较长线段与原线段的比?这就是黄金分割问题.
她的上半
身和下半身的比值接近
0.618.
世界艺术珍品——维纳斯女神
,她是西元前一
百多年希腊雕塑鼎盛时
期的代表作,
黄金分割原理最初运用于雕塑和建筑
数学美的魅力
1
古埃及胡夫金字塔
古希腊巴特农神庙
文明古国埃及的金字塔,形似方锥,大小各异。但这些金字塔底面的边
长与高之比都接近于0.618.
古希腊的一些神庙,在建筑时高和宽也是按黄金比0.618来建立,他们认为这样的长方形看来是较美观;其大理石柱廓,就是根据黄金分割律分割整个神庙的.
你知道芭蕾舞演员跳舞时为什么要掂起脚尖吗?
芭蕾舞演员的身段是苗条的,但下半身与身高的比值也只有0.58左右,演员在表演时掂起脚尖,身高就可以增加6-8cm.这时比值就接近0.618了,给人以更为优美的艺术形象.
芭蕾舞
观察
欣赏
黄金分割
与生活
由黄金分割画出的正五角星形,有庄严雄健之美.
A
B
P
上海东方明珠电视塔高468m,上球体是塔身的黄金分割点,它到塔底部的距离大约是多少米(精确到0.1m)?
468m
?
实际应用
468×0.618≈289.2m
作法:
(1)过已知线段AB的端点B作BC⊥AB
使
例:已知线段AB=a,用直尺和圆规作出它的黄金分割点。
(2)连接AC,在CA上截取CD=CB
(3)在AB上截取AP=AD
问:点P是线段AB唯一的黄金分割点吗
A
B
C
D
P
A
B
a
如图所示,把窗台看成线段AB,点P是
AB的黄金分割点,AP>PB,求
(1)
(2)若AB=2米,则AP=_______米,
PB
=_______米
练习:
A
B
P
把窗台看成线段AB,现把原放置在窗台上点A处的一盆花,移到该线段的黄金分割点上,若AB=2米,试计算这盆花移动后应离A点几米?
变式练习
A
B
C
D
两花盆C、D之间有多远?
课堂小结
通过这节课的学习,你在知识上,方法上都有哪些收获?
1、什么是比例中项。
2、什么是黄金分割。
3、如何去确定黄金分割点或黄金比。
4、要用数学美去装点和美化生活。
如图,设AB是已知线段,以AB为边作正方形ABCD,取AD的中点E,连结EB,延长DA至点F,使EF=EB。以线段AF为边作正方形AFGH,则点H是线段AB的黄金分割点,你能说出这种方法的道理吗?
A
B
C
D
E
F
G
H
1.作顶角为36°的等腰△ABC;量出
底BC与腰AB的长度,计算:
;
2.作∠B的平分线,交AC于点D,量出CD的长度,
再计算:
.
(精确到0.001)
D
C
A
B
E
尝试
0.618
0.618
☆再作∠C的平分线,交BD于E,
△CDE也是黄金三角形……
D
☆顶角为36°的等腰三角形称为
黄金三角形
☆点D是线段AC的黄金分割点.
同课章节目录
