1.1认识三角形同步练习题2021-2022学年八年级数学浙教版上册(Word版 含答案)
文档属性
| 名称 | 1.1认识三角形同步练习题2021-2022学年八年级数学浙教版上册(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 133.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-07 09:45:02 | ||
图片预览


文档简介
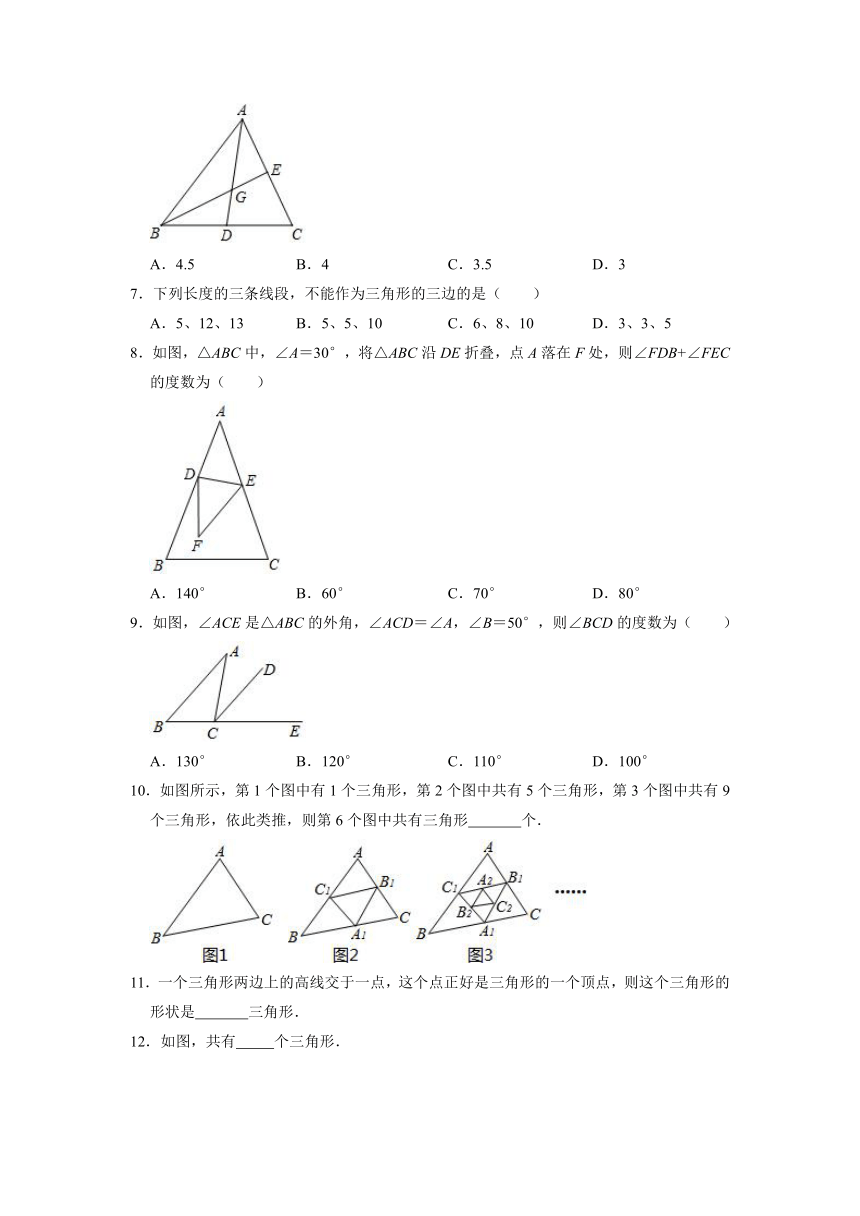
2021-2022学年浙教版八年级数学上册《1.1认识三角形》同步练习题(附答案)
1.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是锐角三角形
B.都是直角三角形
C.都是钝角三角形
D.是一个锐角三角形和一个钝角三角形
2.课堂上,老师把教学用的两块三角板叠放在一起,得到如图所示的图形,其中三角形的个数为( )
A.2
B.3
C.5
D.6
3.如图,Rt△ABC中,∠ABC=90°,BD⊥AC于点D,DE⊥BC于点E,则下列说法中正确的是( )
A.DE是△ACE的高
B.BD是△ADE的高
C.AB是△BCD的高
D.DE是△BCD的高
4.如图,将△ABC沿BC方向平移得到△DEF,AC与DE相交于点G.已知△ABC的面积为18,EC=2BE,则△ABC与△DEF重叠部分(即△CEG)的面积为( )
A.6
B.8
C.9
D.12
5.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上( )根木条.
A.1
B.2
C.3
D.4
6.如图,在△ABC中,D,E分别是BC,AC的中点,AD与BE交于点G.若BG=6,则EG=( )
A.4.5
B.4
C.3.5
D.3
7.下列长度的三条线段,不能作为三角形的三边的是( )
A.5、12、13
B.5、5、10
C.6、8、10
D.3、3、5
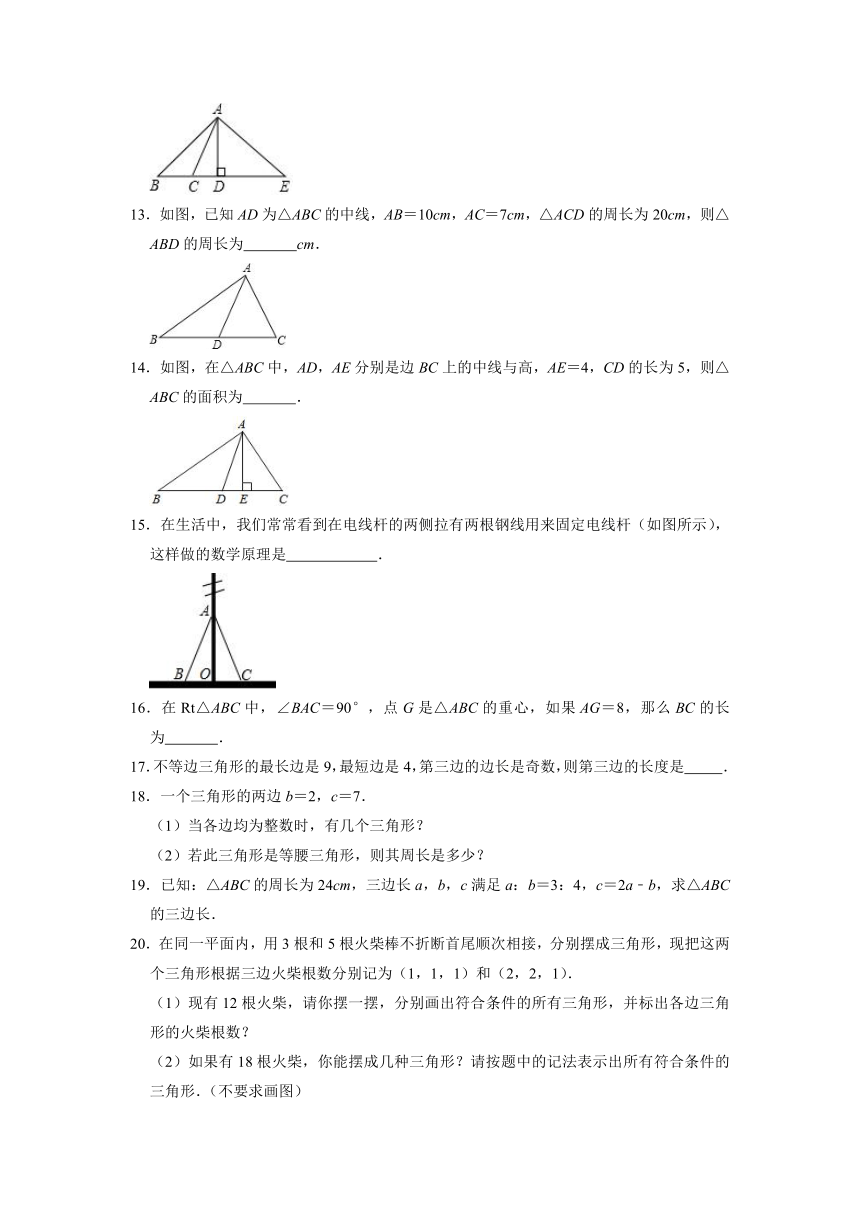
8.如图,△ABC中,∠A=30°,将△ABC沿DE折叠,点A落在F处,则∠FDB+∠FEC的度数为( )
A.140°
B.60°
C.70°
D.80°
9.如图,∠ACE是△ABC的外角,∠ACD=∠A,∠B=50°,则∠BCD的度数为( )
A.130°
B.120°
C.110°
D.100°
10.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形
个.
11.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是
三角形.
12.如图,共有
个三角形.
13.如图,已知AD为△ABC的中线,AB=10cm,AC=7cm,△ACD的周长为20cm,则△ABD的周长为
cm.
14.如图,在△ABC中,AD,AE分别是边BC上的中线与高,AE=4,CD的长为5,则△ABC的面积为
.
15.在生活中,我们常常看到在电线杆的两侧拉有两根钢线用来固定电线杆(如图所示),这样做的数学原理是
.
16.在Rt△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=8,那么BC的长为
.
17.不等边三角形的最长边是9,最短边是4,第三边的边长是奇数,则第三边的长度是
.
18.一个三角形的两边b=2,c=7.
(1)当各边均为整数时,有几个三角形?
(2)若此三角形是等腰三角形,则其周长是多少?
19.已知:△ABC的周长为24cm,三边长a,b,c满足a:b=3:4,c=2a﹣b,求△ABC的三边长.
20.在同一平面内,用3根和5根火柴棒不折断首尾顺次相接,分别摆成三角形,现把这两个三角形根据三边火柴根数分别记为(1,1,1)和(2,2,1).
(1)现有12根火柴,请你摆一摆,分别画出符合条件的所有三角形,并标出各边三角形的火柴根数?
(2)如果有18根火柴,你能摆成几种三角形?请按题中的记法表示出所有符合条件的三角形.(不要求画图)
21.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
22.阅读材料,解决问题.
在平面内,画出原点重合的两条互相垂直的数轴,就组成了一个平面直角坐标系.其中,水平方向的数轴叫做x轴,竖直方向的数轴叫做y轴,原点叫做坐标原点.设P是平面直角坐标系中的一点,作PM⊥x轴于M,PN⊥y轴于N,如果点M和点N在x轴和y轴上所对应的数分别是m和n,那么数m叫做点P的横坐标,数n叫做点P的纵坐标,把m和n合在一起叫做点P的坐标,记作P(m,n),如图所示点P的坐标为(﹣3,4).
(1)点A(4,﹣5)的横坐标为
,纵坐标为
;
(2)在平面直角坐标系中作出点B(﹣1,﹣1),C(1,3);
(3)若过点C(1,3)的直线l与x轴平行,写出一个直线l上不同于点C的点的坐标为
;
(4)过点C(1,3)与x轴平行的直线l,与过点B(﹣1,﹣1)平行于y轴的直线a交于点E,求三角形BCE的面积.
参考答案
1.解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,锐角三角形沿虚线剪开即可得到一个锐角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:A.
2.解:图中三角形的个数是5个,
故选:C.
3.解:∵∠ABC=90°,BD⊥AC于点D,DE⊥BC于点E,
∴DE是△CDB的高,BD是△ABC的高,AB是△ABC的高,
故选:D.
4.解:由平移可知,GE∥AB,
故可得△CEG∽△CBA,
∴,
∴=,
又△ABC的面积为18,
∴S△CEG=18×=8.
故选:B.
5.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
故选:C.
6.解:∵D,E分别是BC,AC的中点,AD与BE交于点G.
∴G点为△ABC的重心,
∴GE=BG=×6=3.
故选:D.
7.解:A、∵5+12>13,∴能构成三角形,不符合题意;
B、∵5+5=10,∴不能构成三角形,符合题意;
C、∵6+8>10,∴能构成三角形,不符合题意;
D、∵3+3>5,∴能构成三角形,不符合题意.
故选:B.
8.解:∵△DEF是由△DEA折叠而成的,
∴∠A=∠F=30°.
∵∠A+∠ADF+∠AEF+∠F=360°,
∴∠ADF+∠AEF=360°﹣∠A﹣∠F=300°.
∵∠BDF=180°﹣∠ADF,
∠FEC=180°﹣∠AEF,
∴∠FDB+∠FEC=180°﹣∠ADF+180°﹣∠AEF
=360°﹣(∠ADF+∠AEF)
=360°﹣300°
=60°.
故选:B.
9.解:∵∠ACD=∠A,
∴AB∥CD,
∴∠B+∠BCD=180°,
∴∠BCD=180°﹣50°=130°,
故选:A.
10.解:第n个图形中,三角形的个数是1+4(n﹣1)=4n﹣3.所以当n=6时,原式=21,
故答案为:21.
11.解:∵三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,
∴这个三角形一定是直角三角形.
故答案为:直角.
12.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故答案为:6
13.解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC=10﹣7=3(cm),
∵△ACD的周长为20cm,AB比AC长3cm,
∴△ABD周长为:20+3=23(cm).
故答案为23.
14.解:∵AD是边BC上的中线,CD的长为5,
∴BC=2CD=10.
∴S△ABC=BC?AE==20.
故答案是:20.
15.解:结合图形,为了防止电线杆倾倒,常常在电线杆上拉两根钢筋来加固电线杆,所以这样做根据的数学道理是三角形的稳定性.
故答案是:三角形的稳定性.
16.解:延长AG交BC于D,如图:
∵点G是△ABC的重心,
∴AD是△ABC的中线,AG=2DG,
∵AG=8,
∴DG=4,AD=AG+DG=12,
∵∠BAC=90°,AD是△ABC的中线,
∴BC=2AD=24,
故答案为:24.
17.解:设第三边长是c,则9﹣4<c<9+4,
即5<c<13,
又∵第三边的长是奇数,不等边三角形的最长边为9,最短边为4,
∴c=7.
故答案为:7.
18.解:(1)设第三边长为a,则5<a<9,
由于三角形的各边均为整数,则a=6或7或8,因此有三个三角形;
(2)当a=7时,有a=7=c,所以周长为7+7+2=16.
19.解:由题意得,
解得:.
故△ABC的三边长为8cm,cm,cm.
20.解:(1)根据边长都为正数和周长为12,以及三角形边长的关系可得出所有的符合条件的三角形分别为(2,5,5),(3,4,5),(4,4,4);
(2)(2,8,8),(3,7,8),(4,7,7),(4,6,8),(5,6,7),(5,5,8),(6,6,6).
21.解:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=13cm,
∴AC=9cm.
即AC的长度是9cm.
22.解:(1)点A(4,﹣5)的横坐标为4,纵坐标为﹣5,
故答案为4,﹣5;
(2)如图所示,
(3)∵过点C(1,3)的直线l与x轴平行,
∴直线l上所有点的纵坐标为3,
∴不同于点C的点的坐标为(2,3),
故答案为(2,3)(答案不唯一);
(4)∵过点C(1,3)与x轴平行的直线l,与过点B(﹣1,﹣1)平行于y轴的直线a交于点E,
∴点E(﹣1,3),
∴EC=2,BE=4,
∴S△BEC=×BE×EC=4.
1.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是锐角三角形
B.都是直角三角形
C.都是钝角三角形
D.是一个锐角三角形和一个钝角三角形
2.课堂上,老师把教学用的两块三角板叠放在一起,得到如图所示的图形,其中三角形的个数为( )
A.2
B.3
C.5
D.6
3.如图,Rt△ABC中,∠ABC=90°,BD⊥AC于点D,DE⊥BC于点E,则下列说法中正确的是( )
A.DE是△ACE的高
B.BD是△ADE的高
C.AB是△BCD的高
D.DE是△BCD的高
4.如图,将△ABC沿BC方向平移得到△DEF,AC与DE相交于点G.已知△ABC的面积为18,EC=2BE,则△ABC与△DEF重叠部分(即△CEG)的面积为( )
A.6
B.8
C.9
D.12
5.如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上( )根木条.
A.1
B.2
C.3
D.4
6.如图,在△ABC中,D,E分别是BC,AC的中点,AD与BE交于点G.若BG=6,则EG=( )
A.4.5
B.4
C.3.5
D.3
7.下列长度的三条线段,不能作为三角形的三边的是( )
A.5、12、13
B.5、5、10
C.6、8、10
D.3、3、5
8.如图,△ABC中,∠A=30°,将△ABC沿DE折叠,点A落在F处,则∠FDB+∠FEC的度数为( )
A.140°
B.60°
C.70°
D.80°
9.如图,∠ACE是△ABC的外角,∠ACD=∠A,∠B=50°,则∠BCD的度数为( )
A.130°
B.120°
C.110°
D.100°
10.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依此类推,则第6个图中共有三角形
个.
11.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是
三角形.
12.如图,共有
个三角形.
13.如图,已知AD为△ABC的中线,AB=10cm,AC=7cm,△ACD的周长为20cm,则△ABD的周长为
cm.
14.如图,在△ABC中,AD,AE分别是边BC上的中线与高,AE=4,CD的长为5,则△ABC的面积为
.
15.在生活中,我们常常看到在电线杆的两侧拉有两根钢线用来固定电线杆(如图所示),这样做的数学原理是
.
16.在Rt△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=8,那么BC的长为
.
17.不等边三角形的最长边是9,最短边是4,第三边的边长是奇数,则第三边的长度是
.
18.一个三角形的两边b=2,c=7.
(1)当各边均为整数时,有几个三角形?
(2)若此三角形是等腰三角形,则其周长是多少?
19.已知:△ABC的周长为24cm,三边长a,b,c满足a:b=3:4,c=2a﹣b,求△ABC的三边长.
20.在同一平面内,用3根和5根火柴棒不折断首尾顺次相接,分别摆成三角形,现把这两个三角形根据三边火柴根数分别记为(1,1,1)和(2,2,1).
(1)现有12根火柴,请你摆一摆,分别画出符合条件的所有三角形,并标出各边三角形的火柴根数?
(2)如果有18根火柴,你能摆成几种三角形?请按题中的记法表示出所有符合条件的三角形.(不要求画图)
21.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
22.阅读材料,解决问题.
在平面内,画出原点重合的两条互相垂直的数轴,就组成了一个平面直角坐标系.其中,水平方向的数轴叫做x轴,竖直方向的数轴叫做y轴,原点叫做坐标原点.设P是平面直角坐标系中的一点,作PM⊥x轴于M,PN⊥y轴于N,如果点M和点N在x轴和y轴上所对应的数分别是m和n,那么数m叫做点P的横坐标,数n叫做点P的纵坐标,把m和n合在一起叫做点P的坐标,记作P(m,n),如图所示点P的坐标为(﹣3,4).
(1)点A(4,﹣5)的横坐标为
,纵坐标为
;
(2)在平面直角坐标系中作出点B(﹣1,﹣1),C(1,3);
(3)若过点C(1,3)的直线l与x轴平行,写出一个直线l上不同于点C的点的坐标为
;
(4)过点C(1,3)与x轴平行的直线l,与过点B(﹣1,﹣1)平行于y轴的直线a交于点E,求三角形BCE的面积.
参考答案
1.解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,锐角三角形沿虚线剪开即可得到一个锐角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:A.
2.解:图中三角形的个数是5个,
故选:C.
3.解:∵∠ABC=90°,BD⊥AC于点D,DE⊥BC于点E,
∴DE是△CDB的高,BD是△ABC的高,AB是△ABC的高,
故选:D.
4.解:由平移可知,GE∥AB,
故可得△CEG∽△CBA,
∴,
∴=,
又△ABC的面积为18,
∴S△CEG=18×=8.
故选:B.
5.解:根据三角形的稳定性,要使六边形木架不变形,至少再钉上3根木条;
故选:C.
6.解:∵D,E分别是BC,AC的中点,AD与BE交于点G.
∴G点为△ABC的重心,
∴GE=BG=×6=3.
故选:D.
7.解:A、∵5+12>13,∴能构成三角形,不符合题意;
B、∵5+5=10,∴不能构成三角形,符合题意;
C、∵6+8>10,∴能构成三角形,不符合题意;
D、∵3+3>5,∴能构成三角形,不符合题意.
故选:B.
8.解:∵△DEF是由△DEA折叠而成的,
∴∠A=∠F=30°.
∵∠A+∠ADF+∠AEF+∠F=360°,
∴∠ADF+∠AEF=360°﹣∠A﹣∠F=300°.
∵∠BDF=180°﹣∠ADF,
∠FEC=180°﹣∠AEF,
∴∠FDB+∠FEC=180°﹣∠ADF+180°﹣∠AEF
=360°﹣(∠ADF+∠AEF)
=360°﹣300°
=60°.
故选:B.
9.解:∵∠ACD=∠A,
∴AB∥CD,
∴∠B+∠BCD=180°,
∴∠BCD=180°﹣50°=130°,
故选:A.
10.解:第n个图形中,三角形的个数是1+4(n﹣1)=4n﹣3.所以当n=6时,原式=21,
故答案为:21.
11.解:∵三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,
∴这个三角形一定是直角三角形.
故答案为:直角.
12.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故答案为:6
13.解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC=10﹣7=3(cm),
∵△ACD的周长为20cm,AB比AC长3cm,
∴△ABD周长为:20+3=23(cm).
故答案为23.
14.解:∵AD是边BC上的中线,CD的长为5,
∴BC=2CD=10.
∴S△ABC=BC?AE==20.
故答案是:20.
15.解:结合图形,为了防止电线杆倾倒,常常在电线杆上拉两根钢筋来加固电线杆,所以这样做根据的数学道理是三角形的稳定性.
故答案是:三角形的稳定性.
16.解:延长AG交BC于D,如图:
∵点G是△ABC的重心,
∴AD是△ABC的中线,AG=2DG,
∵AG=8,
∴DG=4,AD=AG+DG=12,
∵∠BAC=90°,AD是△ABC的中线,
∴BC=2AD=24,
故答案为:24.
17.解:设第三边长是c,则9﹣4<c<9+4,
即5<c<13,
又∵第三边的长是奇数,不等边三角形的最长边为9,最短边为4,
∴c=7.
故答案为:7.
18.解:(1)设第三边长为a,则5<a<9,
由于三角形的各边均为整数,则a=6或7或8,因此有三个三角形;
(2)当a=7时,有a=7=c,所以周长为7+7+2=16.
19.解:由题意得,
解得:.
故△ABC的三边长为8cm,cm,cm.
20.解:(1)根据边长都为正数和周长为12,以及三角形边长的关系可得出所有的符合条件的三角形分别为(2,5,5),(3,4,5),(4,4,4);
(2)(2,8,8),(3,7,8),(4,7,7),(4,6,8),(5,6,7),(5,5,8),(6,6,6).
21.解:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=13cm,
∴AC=9cm.
即AC的长度是9cm.
22.解:(1)点A(4,﹣5)的横坐标为4,纵坐标为﹣5,
故答案为4,﹣5;
(2)如图所示,
(3)∵过点C(1,3)的直线l与x轴平行,
∴直线l上所有点的纵坐标为3,
∴不同于点C的点的坐标为(2,3),
故答案为(2,3)(答案不唯一);
(4)∵过点C(1,3)与x轴平行的直线l,与过点B(﹣1,﹣1)平行于y轴的直线a交于点E,
∴点E(﹣1,3),
∴EC=2,BE=4,
∴S△BEC=×BE×EC=4.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
