2021-2022学年浙教版九年级数学上册3.3 垂径定理课件(26张)
文档属性
| 名称 | 2021-2022学年浙教版九年级数学上册3.3 垂径定理课件(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 08:23:38 | ||
图片预览






文档简介
(共26张PPT)
义务教育课程标准实验教科书
浙江版《数学》九年级上册
3.3垂径定理(2)
一、教学目标:
1、经历探索垂径定理的逆定理的过程。
2、掌握定理“平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧”及定理“平分弧的直径垂直平分弧所对的弦”。
3、会运用垂径定理的逆定理解决一些简单的几何问题。
二、教学重点:
垂径定理的逆定理
三、教学难点:
例3的问题情境比较复杂,是本节教学的难点
四、教材分析:
学生在上一节课中已经学习了垂径定理,并能用垂径定理解决一些简单的几何问题本节课关键是推导出垂径定理的逆定理并加以应用。
五、教学设计:
善于自学——勤于巩固——乐于合作——勤于巩固
义务教育课程标准实验教科书
浙江版《数学》九年级上册
3.3垂径定理(2)
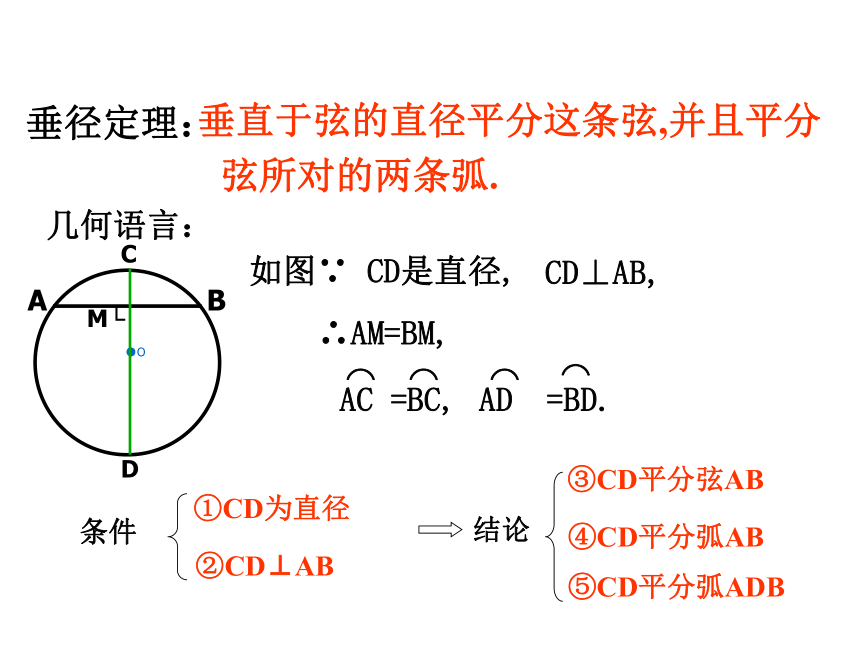
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵
CD是直径,
∴AM=BM,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
条件
①CD为直径
②CD⊥AB
⑤CD平分弧ADB
③CD平分弦AB
④CD平分弧AB
结论
温故知新
垂径定理:
几何语言:
1.垂径定理的逆命题是什么?
垂直于弦的直径平分这条弦,并且平分弦所
对的弧.
条件
结论1
结论2
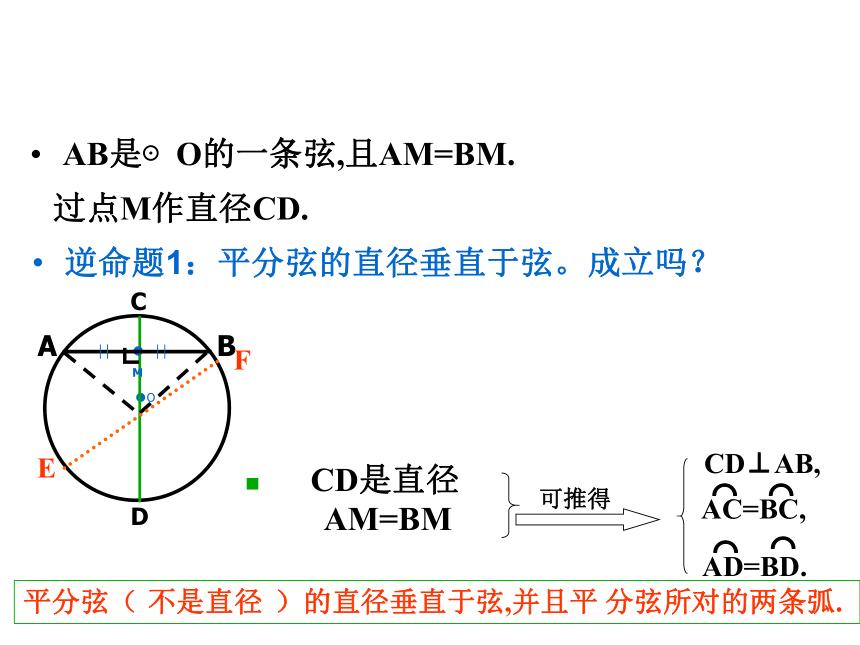
逆命题1:平分弦的直径垂直于弦。
逆命题2:平分弧的直径垂直于弧所对的弦。
善于自学
2.垂径定理的逆命题是真命题吗?如何证明?
结合下面问题预习书本P79
3.垂径定理的逆定理用几何语言如何叙述?
CD⊥AB,
AB是⊙O的一条弦,且AM=BM.
逆命题1:平分弦的直径垂直于弦。成立吗?
过点M作直径CD.
●O
C
D
CD是直径
AM=BM
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
●
M
A
B
┗
平分弦(
)的直径垂直于弦,并且平
分弦所对的两条弧.
不是直径
E
F
善于自学
.
O
A
E
B
D
C
已知:⊙O的直径CD交弦AB(不是直径)于点E,且AE=BE
求证:CD⊥AB,AD=BD,AC=BC
⌒
⌒
⌒
⌒
命题1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
证明:连结OA,OB,则OA=OB
∴△AOB是等腰三角形
∵AE=BE
∴CD⊥AB
(等腰三角形三线合一)
(垂径定理)
∴AD=BD,AC=BC
⌒
⌒
⌒
⌒
CD⊥AB,
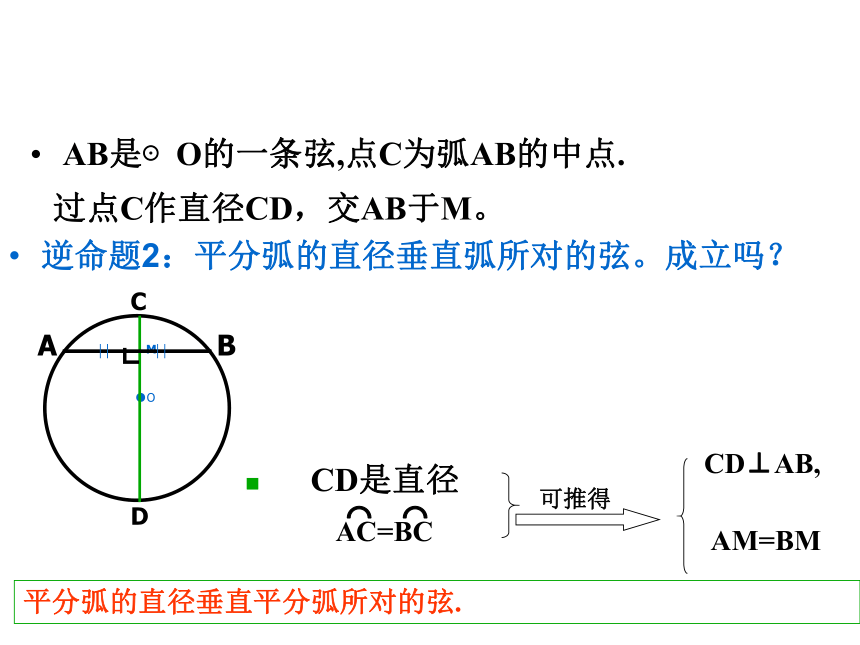
AB是⊙O的一条弦,点C为弧AB的中点.
逆命题2:平分弧的直径垂直弧所对的弦。成立吗?
过点C作直径CD,交AB于M。
●O
C
D
CD是直径
可推得
M
A
B
┗
平分弧的直径垂直平分弧所对的弦.
⌒
⌒
AC=BC
AM=BM
善于自学
垂直于弦的直径平分这条弦,并且平分弦所对的弧
逆定理
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
定理2:平分弧的直径垂直平分弧所对的弦
垂径定理
只要具备其中两个条件,就可推出其余三个结论.
●O
A
B
C
D
M└
①
CD是直径,
③
AM=BM,
②
CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
如图,
对于一个圆和一条直线来说。如果在下列五个条件中:
1.已知,如图,在以点O为圆心的两个圆中,大
圆的弦AB和小圆交于点C,D,求证:AC=BD
解:过O作OE⊥AB于E点,
则AE=BE,CE=DE
(________________________)
∴AE-CE=BE-DE
即AC=BD
垂直弦的直径平分这条弦
E
勤于巩固1
·
A
B
C
D
0
E
F
G
H
2、如图,圆O与矩形ABCD交于E、F、G、H,
EF=10,HG=6,AH=4.求BE的长.
M
(1)垂直于弦的直线平分弦,并且平分弦所对的弧
(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心
(3)圆的不与直径垂直的弦必不被这条直径平分
(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧
(5)圆内两条非直径的弦不能互相平分
×
√
×
×
√
3.辨一辨
(6)平分弦的直径,平分这条弦所对的弧。
(7)平分弦的直线,必定过圆心。
(8)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。
?
?
?
A
B
C
D
O
(1)
A
B
C
D
?O
(2)
A
B
C
D
?O
(3)
(9)弦的垂直平分线一定是圆的直径。
(10)平分弧的直线,平分这条弧所对的弦。
(11)弦垂直于直径,这条直径就被弦平分。
?
?
?
A
B
C
?O
(4)
A
B
C
D
?O
(5)
A
B
C
D
?O
(6)
E
例3、1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为
37.02
m,拱高(弧的中点到弦的距离,也叫弓形高)为7.23m,求桥拱的半径(精确到0.
1m).
乐于合作
B
O
D
R
A
C
结合下面问题先自学书本P79例3再交流:
画出简单几何图形,标明已知数据
这里出现弧的中点以及拱高,想到什么定理?如何作辅助线
如何用含半径R的代数式表示OD的长?
如何求出R值?
A
B
O
C
D
AB表示桥拱,设AB所在的圆的圆心为O,半径为R,C为AB的中点,连结OC,交AB于点D
R
解:
∴OC⊥AB
∴CD就是拱高
∴AD=1/2AB=0.5×37.02=18.51
OD=OC-DC=(R-7.23)
在Rt△OAD中,OA2=OD2+AD2
∴R2=18.512+(R-7.23)2
解得,R≈27.3
答:赵州桥的桥拱半径约为27.3m.
∵C是AB的中点
⌒
勤于巩固2
1、完成书本P80课内练习2和作业题2、4、5
2、完成书本P80课内练习1
提示:
这两条弦在圆中位置有两种情况:
●O
A
B
C
D
(1)两条弦在圆心的同侧
●O
A
B
C
D
(2)两条弦在圆心的两侧
垂径定理的推论:圆的两条平行弦所夹的弧相等.
3、求证:如果圆的两条弦互相平行,那么这两条弦所夹的弧相等
E
F
E
●O
C
D
A
B
当两条弦在圆心的同侧时
●O
C
D
A
B
解:
当两条弦在圆心的两侧时
4.
已知圆O的半径为5cm,弦AB∥弦CD,AB=6cm,CD=8cm,
则AB与CD距离是__________cm
F
E
过O作OE⊥AB于E点,连接OB,
由垂径定理得:AE=BE=0.5AB=3
延长EO交CD于F,连接OC
3
3
5
OB=5,由勾股定理得:OE=4
又∵AB∥CD
∴OF⊥CD
由垂径定理得:
CF=DF=0.5CD=4
OC=5,由勾股定理得:OF=3
则EF=OE+OF=7
4
4
4
5
3
3
4
5
5
F
E
EF=OE-OF=1
喜于收获
今天你有什么收获?还有什么疑问?
2.解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
1.垂径定理的两个逆定理和一个推论:
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
定理2:平分弧的直径垂直平分弧所对的弦
垂径定理的推论:圆的两条平行弦所夹的弧相等.
作业
1、作业本3.3(2)
2、全效3.3(2)
拓展提高
1、
如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
2.某一公路隧道的形状如图,半圆拱的圆心距离地面2m,半径为1.5m,一辆高3m,宽2.3m的集装箱车能通过这个隧道吗?
F
1.15
解:取CD=1.15m,作DE⊥CD交圆O于点E
连接OE,过O作OF⊥ED于F,
由题意可得OE=1.5,OF=CD=1.15
FD=OC=2由勾股定理得:
≈0.96
∴DF=EF+DF=2.96<3
∴高3m,宽2.3m的集装箱车
不能通过这个隧道
D
E
1.5
1.15
2
如果要使高度不超过4m,宽为2.3m的货车能通过这个隧道,且不改变圆心到地面的距离,半圆拱的半径至少为多少m?
再见
义务教育课程标准实验教科书
浙江版《数学》九年级上册
3.3垂径定理(2)
一、教学目标:
1、经历探索垂径定理的逆定理的过程。
2、掌握定理“平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧”及定理“平分弧的直径垂直平分弧所对的弦”。
3、会运用垂径定理的逆定理解决一些简单的几何问题。
二、教学重点:
垂径定理的逆定理
三、教学难点:
例3的问题情境比较复杂,是本节教学的难点
四、教材分析:
学生在上一节课中已经学习了垂径定理,并能用垂径定理解决一些简单的几何问题本节课关键是推导出垂径定理的逆定理并加以应用。
五、教学设计:
善于自学——勤于巩固——乐于合作——勤于巩固
义务教育课程标准实验教科书
浙江版《数学》九年级上册
3.3垂径定理(2)
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵
CD是直径,
∴AM=BM,
⌒
⌒
AC
=BC,
⌒
⌒
AD
=BD.
条件
①CD为直径
②CD⊥AB
⑤CD平分弧ADB
③CD平分弦AB
④CD平分弧AB
结论
温故知新
垂径定理:
几何语言:
1.垂径定理的逆命题是什么?
垂直于弦的直径平分这条弦,并且平分弦所
对的弧.
条件
结论1
结论2
逆命题1:平分弦的直径垂直于弦。
逆命题2:平分弧的直径垂直于弧所对的弦。
善于自学
2.垂径定理的逆命题是真命题吗?如何证明?
结合下面问题预习书本P79
3.垂径定理的逆定理用几何语言如何叙述?
CD⊥AB,
AB是⊙O的一条弦,且AM=BM.
逆命题1:平分弦的直径垂直于弦。成立吗?
过点M作直径CD.
●O
C
D
CD是直径
AM=BM
可推得
⌒
⌒
AC=BC,
⌒
⌒
AD=BD.
●
M
A
B
┗
平分弦(
)的直径垂直于弦,并且平
分弦所对的两条弧.
不是直径
E
F
善于自学
.
O
A
E
B
D
C
已知:⊙O的直径CD交弦AB(不是直径)于点E,且AE=BE
求证:CD⊥AB,AD=BD,AC=BC
⌒
⌒
⌒
⌒
命题1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
证明:连结OA,OB,则OA=OB
∴△AOB是等腰三角形
∵AE=BE
∴CD⊥AB
(等腰三角形三线合一)
(垂径定理)
∴AD=BD,AC=BC
⌒
⌒
⌒
⌒
CD⊥AB,
AB是⊙O的一条弦,点C为弧AB的中点.
逆命题2:平分弧的直径垂直弧所对的弦。成立吗?
过点C作直径CD,交AB于M。
●O
C
D
CD是直径
可推得
M
A
B
┗
平分弧的直径垂直平分弧所对的弦.
⌒
⌒
AC=BC
AM=BM
善于自学
垂直于弦的直径平分这条弦,并且平分弦所对的弧
逆定理
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
定理2:平分弧的直径垂直平分弧所对的弦
垂径定理
只要具备其中两个条件,就可推出其余三个结论.
●O
A
B
C
D
M└
①
CD是直径,
③
AM=BM,
②
CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
如图,
对于一个圆和一条直线来说。如果在下列五个条件中:
1.已知,如图,在以点O为圆心的两个圆中,大
圆的弦AB和小圆交于点C,D,求证:AC=BD
解:过O作OE⊥AB于E点,
则AE=BE,CE=DE
(________________________)
∴AE-CE=BE-DE
即AC=BD
垂直弦的直径平分这条弦
E
勤于巩固1
·
A
B
C
D
0
E
F
G
H
2、如图,圆O与矩形ABCD交于E、F、G、H,
EF=10,HG=6,AH=4.求BE的长.
M
(1)垂直于弦的直线平分弦,并且平分弦所对的弧
(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心
(3)圆的不与直径垂直的弦必不被这条直径平分
(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧
(5)圆内两条非直径的弦不能互相平分
×
√
×
×
√
3.辨一辨
(6)平分弦的直径,平分这条弦所对的弧。
(7)平分弦的直线,必定过圆心。
(8)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。
?
?
?
A
B
C
D
O
(1)
A
B
C
D
?O
(2)
A
B
C
D
?O
(3)
(9)弦的垂直平分线一定是圆的直径。
(10)平分弧的直线,平分这条弧所对的弦。
(11)弦垂直于直径,这条直径就被弦平分。
?
?
?
A
B
C
?O
(4)
A
B
C
D
?O
(5)
A
B
C
D
?O
(6)
E
例3、1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为
37.02
m,拱高(弧的中点到弦的距离,也叫弓形高)为7.23m,求桥拱的半径(精确到0.
1m).
乐于合作
B
O
D
R
A
C
结合下面问题先自学书本P79例3再交流:
画出简单几何图形,标明已知数据
这里出现弧的中点以及拱高,想到什么定理?如何作辅助线
如何用含半径R的代数式表示OD的长?
如何求出R值?
A
B
O
C
D
AB表示桥拱,设AB所在的圆的圆心为O,半径为R,C为AB的中点,连结OC,交AB于点D
R
解:
∴OC⊥AB
∴CD就是拱高
∴AD=1/2AB=0.5×37.02=18.51
OD=OC-DC=(R-7.23)
在Rt△OAD中,OA2=OD2+AD2
∴R2=18.512+(R-7.23)2
解得,R≈27.3
答:赵州桥的桥拱半径约为27.3m.
∵C是AB的中点
⌒
勤于巩固2
1、完成书本P80课内练习2和作业题2、4、5
2、完成书本P80课内练习1
提示:
这两条弦在圆中位置有两种情况:
●O
A
B
C
D
(1)两条弦在圆心的同侧
●O
A
B
C
D
(2)两条弦在圆心的两侧
垂径定理的推论:圆的两条平行弦所夹的弧相等.
3、求证:如果圆的两条弦互相平行,那么这两条弦所夹的弧相等
E
F
E
●O
C
D
A
B
当两条弦在圆心的同侧时
●O
C
D
A
B
解:
当两条弦在圆心的两侧时
4.
已知圆O的半径为5cm,弦AB∥弦CD,AB=6cm,CD=8cm,
则AB与CD距离是__________cm
F
E
过O作OE⊥AB于E点,连接OB,
由垂径定理得:AE=BE=0.5AB=3
延长EO交CD于F,连接OC
3
3
5
OB=5,由勾股定理得:OE=4
又∵AB∥CD
∴OF⊥CD
由垂径定理得:
CF=DF=0.5CD=4
OC=5,由勾股定理得:OF=3
则EF=OE+OF=7
4
4
4
5
3
3
4
5
5
F
E
EF=OE-OF=1
喜于收获
今天你有什么收获?还有什么疑问?
2.解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
1.垂径定理的两个逆定理和一个推论:
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧
定理2:平分弧的直径垂直平分弧所对的弦
垂径定理的推论:圆的两条平行弦所夹的弧相等.
作业
1、作业本3.3(2)
2、全效3.3(2)
拓展提高
1、
如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?
2.某一公路隧道的形状如图,半圆拱的圆心距离地面2m,半径为1.5m,一辆高3m,宽2.3m的集装箱车能通过这个隧道吗?
F
1.15
解:取CD=1.15m,作DE⊥CD交圆O于点E
连接OE,过O作OF⊥ED于F,
由题意可得OE=1.5,OF=CD=1.15
FD=OC=2由勾股定理得:
≈0.96
∴DF=EF+DF=2.96<3
∴高3m,宽2.3m的集装箱车
不能通过这个隧道
D
E
1.5
1.15
2
如果要使高度不超过4m,宽为2.3m的货车能通过这个隧道,且不改变圆心到地面的距离,半圆拱的半径至少为多少m?
再见
同课章节目录
