1.4 二次函数的应用课件 浙教版九年级数学上册(15张)
文档属性
| 名称 | 1.4 二次函数的应用课件 浙教版九年级数学上册(15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 604.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-08 07:53:20 | ||
图片预览



文档简介
(共15张PPT)
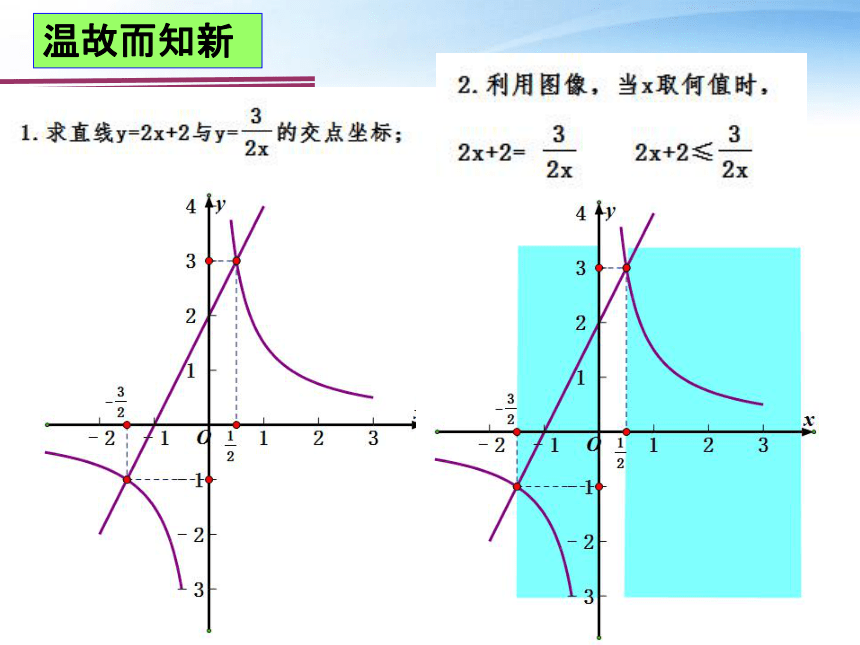
温故而知新
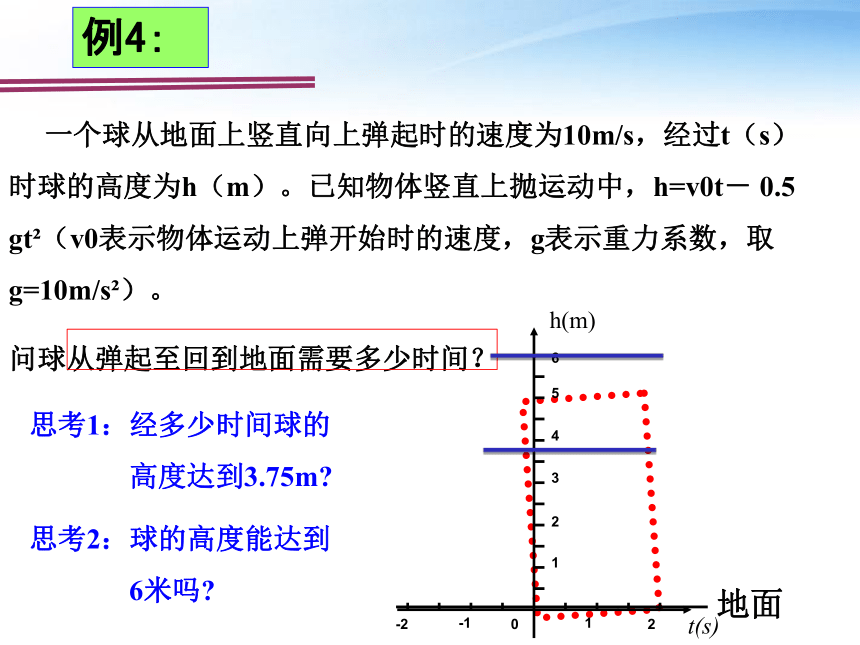
例4:
一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t-
0.5
gt?(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s?)。
问球从弹起至回到地面需要多少时间?
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
思考1:经多少时间球的
高度达到3.75m?
思考2:球的高度能达到
6米吗?
例4:
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t?
取h=0,得一元二次方程
10t-5t?=0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t?=3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
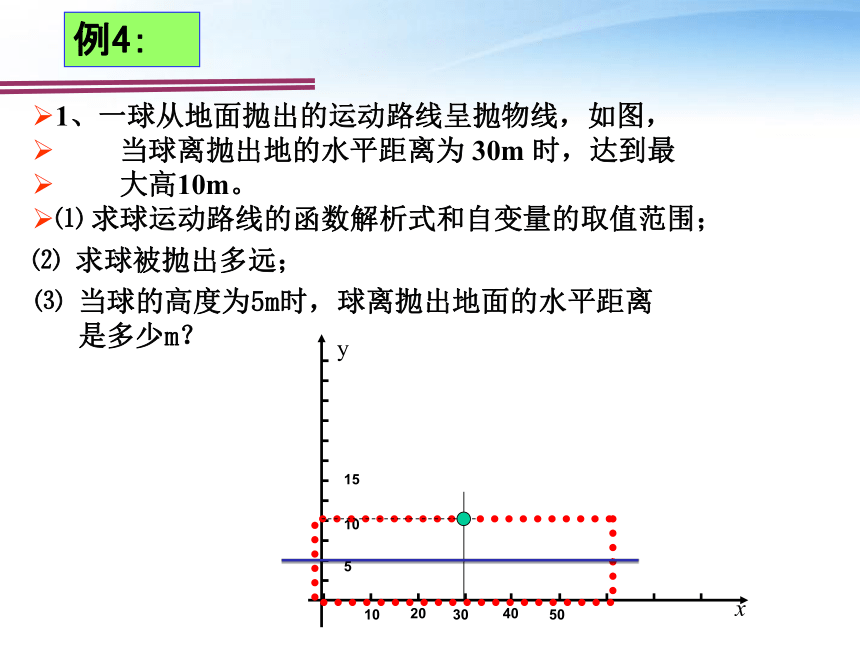
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为
30m
时,达到最
大高10m。
⑴
求球运动路线的函数解析式和自变量的取值范围;
40
50
30
20
10
x
5
10
15
y
⑶
当球的高度为5m时,球离抛出地面的水平距离
是多少m?
⑵
求球被抛出多远;
例4:
二次函数的图象与x轴有没有交点,由什么决定?
复习思考
由b?-4ac的符号决定
b?-4ac﹥0,有两个交点
b?-4ac=0,只有一个交点
b?-4ac﹤0,没有交点
下列函数图象与x轴有没有交点。
①x?=2x-1
②2x?-x+1=0
③2x?-4x-1=0
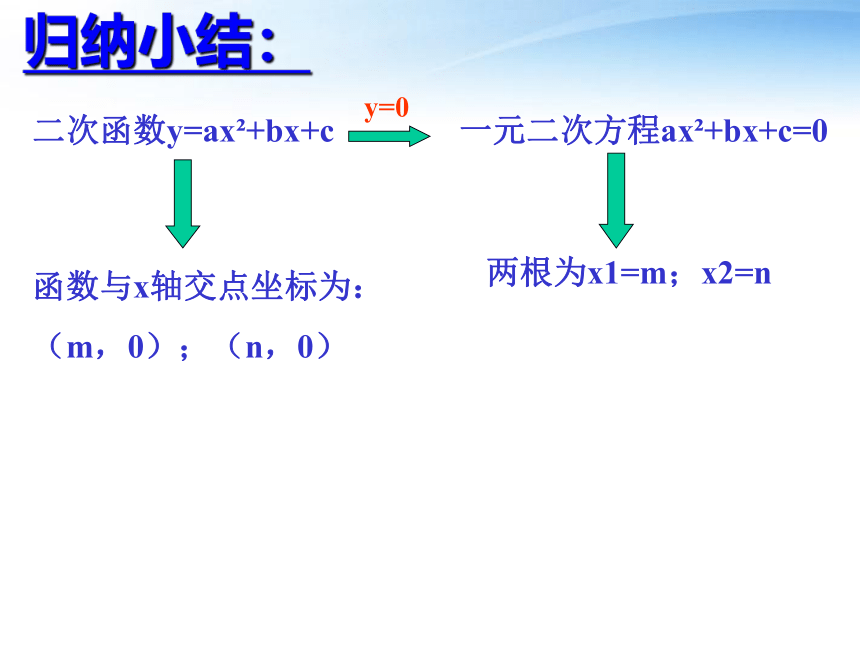
二次函数y=ax?+bx+c
归纳小结:
y=0
一元二次方程ax?+bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
反过来,也可利用二次函数的图象
求一元二次方程的解。
二次函数y=ax?+bx+c
归纳小结:
y=0
一元二次方程ax?+bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
利用二次函数的图象求一元二次方程x?+x-1=
0
的近似解。
例5:
1
2
0
-1
-2
x
1
2
3
4
5
6
y
几何画板操作
两个函数图像__________________交点的横坐标
方程组__________________
的解
◆用求根公式求出方程x?+x-1=0的近似解,并由检验例5中所给图象解法的精确度。
几何画板操作
两个函数图像__________________交点的横坐标
方程组__________________
的解
◆你认为哪种方法较为方便?
几何画板操作
例5—变式1
几何画板操作
例5—变式2
几何画板操作
华罗庚曾说:
“数形本是相倚依,焉能分作两边飞,
数缺形时少直观,形缺数时难入微。”
归纳小结:
一、总结规律找方法
1.
2.
二、善用数学思想
1.
2.
函数图像交点横坐标
对应方程组的解
函数图像的交点个数
对应方程组解的个数
转化思想
数形结合思想
当堂检测:
作业本(2)第5页
基础练习1-3
温故而知新
例4:
一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t-
0.5
gt?(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s?)。
问球从弹起至回到地面需要多少时间?
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
思考1:经多少时间球的
高度达到3.75m?
思考2:球的高度能达到
6米吗?
例4:
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t?
取h=0,得一元二次方程
10t-5t?=0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t?=3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为
30m
时,达到最
大高10m。
⑴
求球运动路线的函数解析式和自变量的取值范围;
40
50
30
20
10
x
5
10
15
y
⑶
当球的高度为5m时,球离抛出地面的水平距离
是多少m?
⑵
求球被抛出多远;
例4:
二次函数的图象与x轴有没有交点,由什么决定?
复习思考
由b?-4ac的符号决定
b?-4ac﹥0,有两个交点
b?-4ac=0,只有一个交点
b?-4ac﹤0,没有交点
下列函数图象与x轴有没有交点。
①x?=2x-1
②2x?-x+1=0
③2x?-4x-1=0
二次函数y=ax?+bx+c
归纳小结:
y=0
一元二次方程ax?+bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
反过来,也可利用二次函数的图象
求一元二次方程的解。
二次函数y=ax?+bx+c
归纳小结:
y=0
一元二次方程ax?+bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
利用二次函数的图象求一元二次方程x?+x-1=
0
的近似解。
例5:
1
2
0
-1
-2
x
1
2
3
4
5
6
y
几何画板操作
两个函数图像__________________交点的横坐标
方程组__________________
的解
◆用求根公式求出方程x?+x-1=0的近似解,并由检验例5中所给图象解法的精确度。
几何画板操作
两个函数图像__________________交点的横坐标
方程组__________________
的解
◆你认为哪种方法较为方便?
几何画板操作
例5—变式1
几何画板操作
例5—变式2
几何画板操作
华罗庚曾说:
“数形本是相倚依,焉能分作两边飞,
数缺形时少直观,形缺数时难入微。”
归纳小结:
一、总结规律找方法
1.
2.
二、善用数学思想
1.
2.
函数图像交点横坐标
对应方程组的解
函数图像的交点个数
对应方程组解的个数
转化思想
数形结合思想
当堂检测:
作业本(2)第5页
基础练习1-3
同课章节目录
