2021—2022学年 高二上学期 人教版 必修三4.2 种群数量的变化 课件(30张ppt)
文档属性
| 名称 | 2021—2022学年 高二上学期 人教版 必修三4.2 种群数量的变化 课件(30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 生物学 | ||
| 更新时间 | 2021-09-09 22:27:17 | ||
图片预览


文档简介
(共30张PPT)
第4章 种群和群落
第2节
种群数量的变化
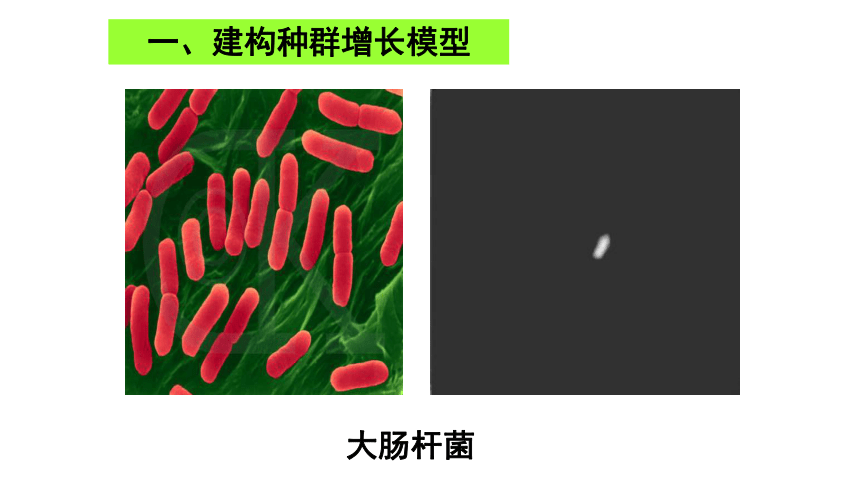
大肠杆菌
一、建构种群增长模型
时间(min)
细胞数
0
20
40
60
80
100
1
2
4
8
16
32
种群数量的变化
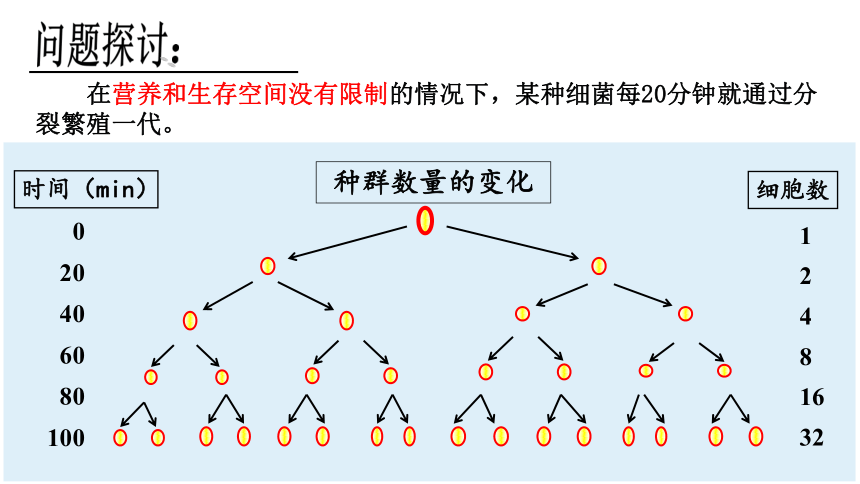
在营养和生存空间没有限制的情况下,某种细菌每20分钟就通过分裂繁殖一代。
问题探讨:
讨论2:根据上表,写出n代细菌数量的计算公式:
讨论3:72小时后,由一个细菌分裂产生的细菌数量是多少?
讨论1:请你计算出一个细菌产生的后代在不同时间的数量:
时间分钟
20
40
60
80
100
120
140
160
180
细菌数量
2
4
8
16
32
64
128
256
512
问题探讨:
Nn
=
1×2n
n=
60min
72h/20min=216
Nn=2n
=2216
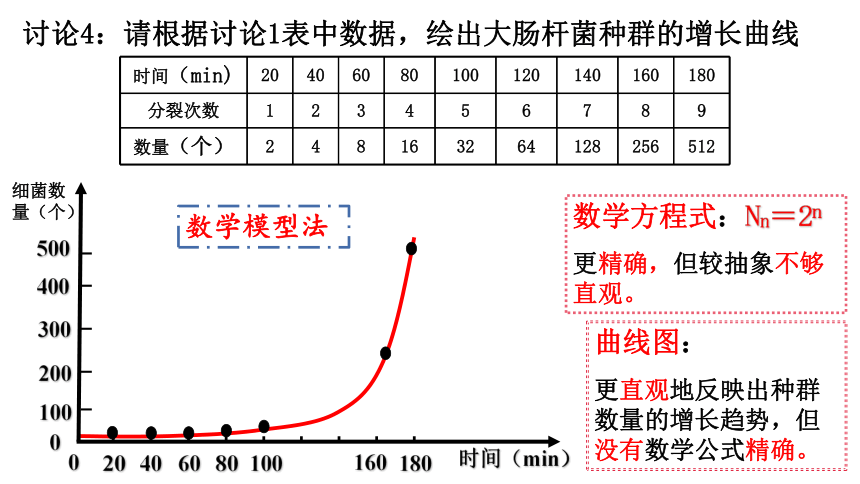
讨论4:请根据讨论1表中数据,绘出大肠杆菌种群的增长曲线
时间(min)
20
40
60
80
100
120
140
160
180
分裂次数
1
2
3
4
5
6
7
8
9
数量(个)
2
4
8
16
32
64
128
256
512
数学方程式:Nn=2n
更精确,但较抽象不够直观。
曲线图:
更直观地反映出种群数量的增长趋势,但没有数学公式精确。
数学模型法
100
200
300
400
500
0
细菌数量(个)
时间(min)
20
40
60
80
100
180
0
160
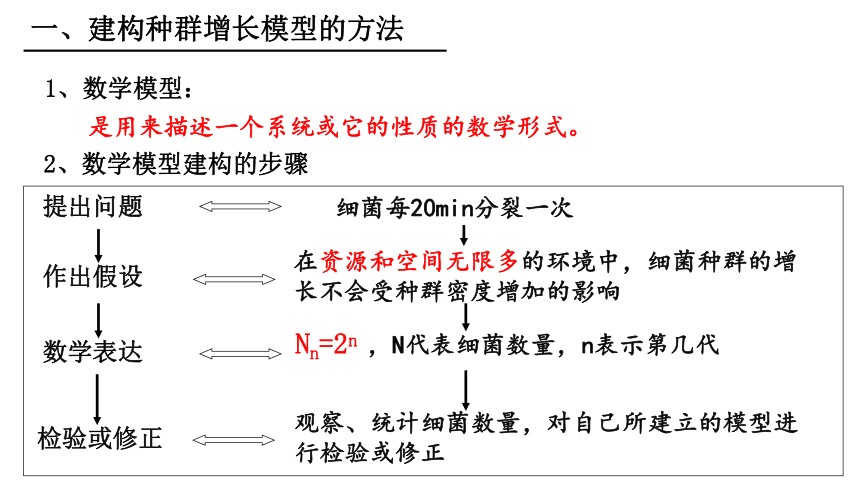
1、数学模型:
是用来描述一个系统或它的性质的数学形式。
2、数学模型建构的步骤
一、建构种群增长模型的方法
提出问题
作出假设
数学表达
检验或修正
细菌每20min分裂一次
在资源和空间无限多的环境中,细菌种群的增长不会受种群密度增加的影响
Nn=2n
,N代表细菌数量,n表示第几代
观察、统计细菌数量,对自己所建立的模型进行检验或修正
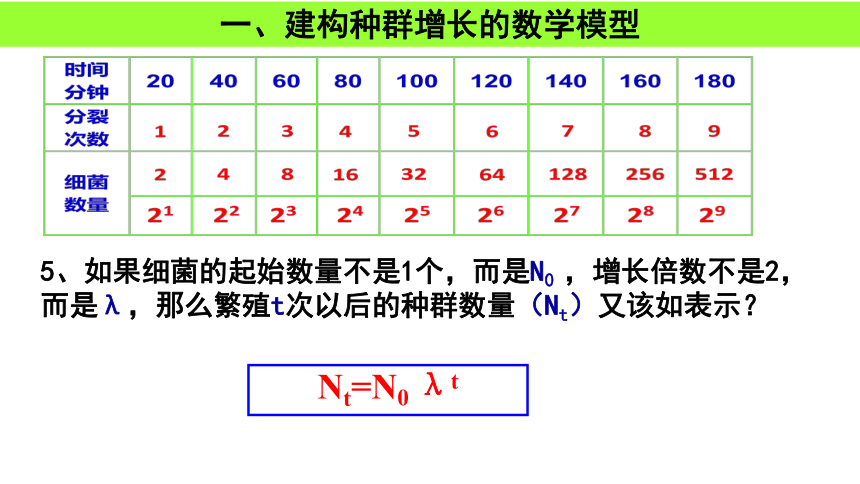
一、建构种群增长的数学模型
5、如果细菌的起始数量不是1个,而是N0
,增长倍数不是2,而是λ,那么繁殖t次以后的种群数量(Nt)又该如表示?
Nt=N0
λt
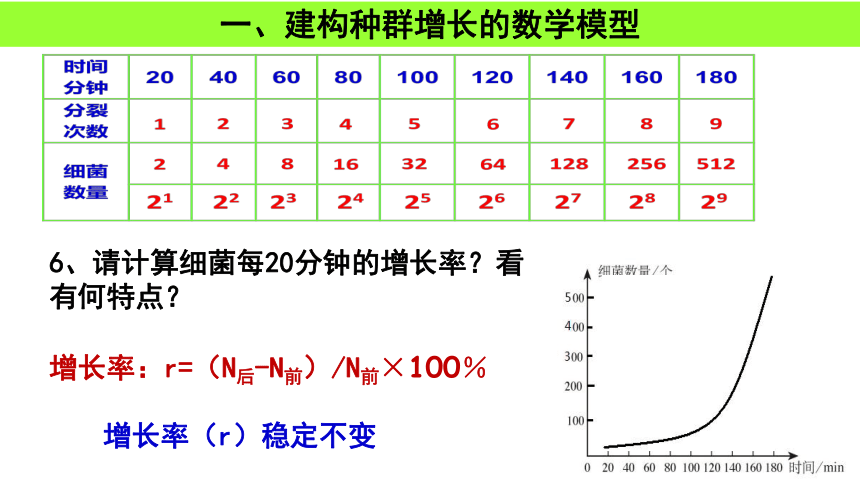
一、建构种群增长的数学模型
6、请计算细菌每20分钟的增长率?看有何特点?
增长率:r=(N后-N前)/N前×100%
增长率(r)稳定不变
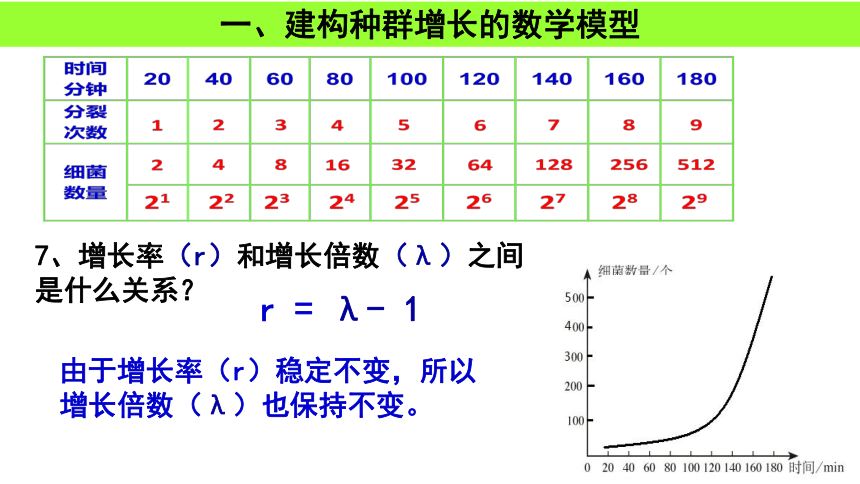
一、建构种群增长的数学模型
7、增长率(r)和增长倍数(λ)之间是什么关系?
r
=
λ-
1
由于增长率(r)稳定不变,所以增长倍数(λ)也保持不变。
一、建构种群增长的数学模型
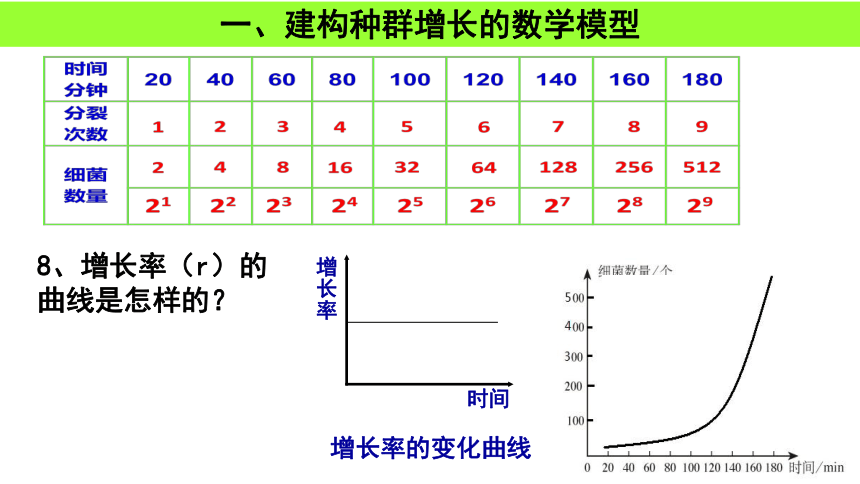
8、增长率(r)的曲线是怎样的?
增长率
时间
增长率的变化曲线
一、建构种群增长的数学模型
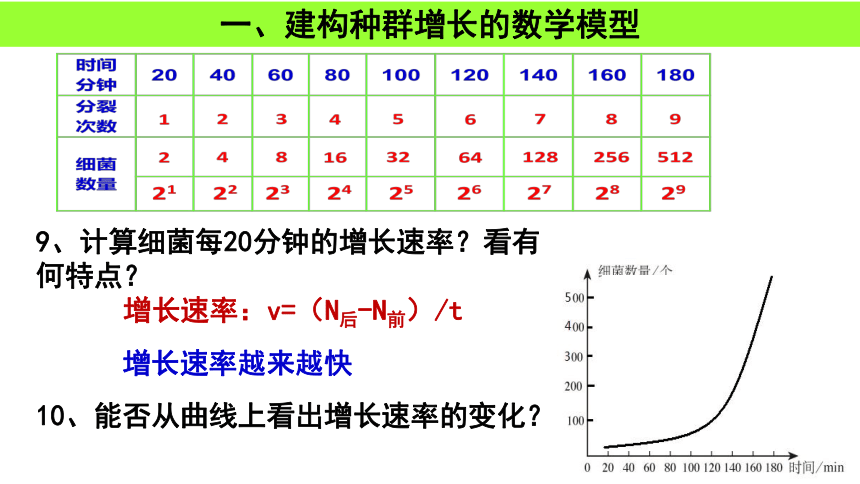
9、计算细菌每20分钟的增长速率?看有何特点?
增长速率:v=(N后-N前)/t
增长速率越来越快
10、能否从曲线上看出增长速率的变化?
一、建构种群增长的数学模型
11、细菌增长的曲线像什么字母?
J
类似细菌在理想条件下的种群增长曲线,称为“J”型曲线。
自然界确有类似的细菌在理想条件下种群数量增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线大致呈“J”型.
时
间
种群数量
二、种群增长的“J”型曲线
①产生条件:
理想状态——食物充足,空间不限,气候适宜,没有天敌等;
②增长特点:
持续增长——种群数量每年以一定的倍数增长,第二年是第一年的λ倍。
③量的计算:t年后种群的数量为
Nt
=
N0λt
注:N0为起始数量,t为时间,Nt表示t年后该种群的数量,λ为一年前种群数量的倍数。
④例:实验室条件下、外来物种入侵、外来物种入侵早期阶段。
指数增长
二、种群增长的“J”型曲线
N0
?
增长率=
末数-初数
初数
增长速率=
末数-初数
单位时间
5.“J”型增长的增长率和增长速率
二、种群增长的“J”型曲线
种群增长率
种群增长速率
(无单位)
“J”型增长能一直持续下去吗?
达尔文估计,一对象,如果保证食物和其他条件,在没有其他生物或天敌危害的情况下,740~750年后就可以繁殖成具有19000000个个体的巨大种群,但是这一现象并没有在自然界中发生。
环境阻力:
食物有限
空间有限
种内斗争
种间竞争
天敌捕食……
高斯对大草履虫种群研究的实验
高斯(Gause,1934)把5个大草履虫置于0.5mL的培养液中,每隔24小时统计一次数据,经过反复实验,结果如下:
时间(天)
0
1
2
3
4
5
6
种群数量(个)
5
20
137
319
369
375
375
K=375
在环境条件不受破坏的情况下,一定空间所能维持的种群的最大数量称为环境容纳量,又称为K值
三、种群增长的“S”型曲线
2.产生条件:
存在环境阻力
1.种群经过一定时间的增长后,数量趋于稳定的增长曲线,称为“S”型曲线.
①资源和空间有限;②种内斗争加剧;③天敌数量增加;④出生率下降,死亡率上升,最终达到平衡。(出生率等于死亡率)
3.特点:种群数量达到环境所允许的最大值(K值)后将停止增长,围绕K值上下波动;当生存环境改变时,K值也会相应改变。
三、种群增长的“S”型曲线
4.
“S”型曲线的特征:
该曲线的斜率变化是怎样的?说明了什么?
B
A
C
K/2
A
B
C
增长速率
曲线的斜率先增后减,说明种群数量的增长速率先增后减。
时间
三、种群增长的“S”型曲线
5.
“S”型曲线的特征:
有最大值,称为_______。
增长速率最大时,种群数量为______,
在K值时增长速率为_______。
K/2
0
B
A
C
K/2
A
B
C
增长速率
K值
时间
6.“S”型增长的增长率和增长速率
K/2
K
种群增长速率
A
B
C
D
K
K/2
②有害生物的防治:
(1)K值的应用
①野生生物资源保护:
减小环境阻力,增大K值。
(如:为防鼠害而封储粮食、清除生活垃圾、保护鼠的天敌等)
增大环境阻力,降低K值。
7.
K值
与
K/2
的应用
控制种群数量,严防达到K/2值处(若达K/2值处,可导致该有害生物成灾,如蝗虫的防控)
(2)K/2的应用
①资源开发与利用:
捕捞后数量要维持在
K/2
,保证最大持续捕捞量,因为在这个水平上种群增长速率最大。
②有害生物防治:
最大日捕捞量:种群数量达到最大值(K值)时捕捞
项目
“J”型曲线
“S”型曲线
曲线
模型
形成条件
增长率
有无K值
增长速率曲线
小结
资源无限的理想条件
资源有限的自然条件
不变
逐渐减小
无K值,持续增加
有K值,可在K值附近上下波动
代表环境阻力—其数量表示生存斗争中被淘汰的个体数。
食物不足、空间有限、种内斗争、天敌捕食、气候不适等
讨论
:图中阴影部分代表的什么?
大多数种群的数量总是在波动之中的,
东亚飞蝗种群数量的波动
四、种群数量的波动和下降
(1)影响种群数量变化的因素:
A.内部/直接因素:出生(死亡)率、迁入(出)率
B.自然/间接因素:空间、气候、食物、天敌、传染病、自然灾害等。
C.人为/重要因素:对野生生物的乱捕滥猎、对种群数量的人工控制
(2)种群数量变化的类型:增长,稳定,波动、下降等。
(3)影响结果:大多数种群的数量总是在波动之中,在不利条件之下,还会急剧下降,甚至灭亡。
课堂练习
1.建构种群增长数学模型的方法包括以下步骤(
)
提出合理的假设
对模型进行检验或修正
用适当的数学形式对事物的性质进行表达
观察研究对象,提出问题
A.1234
B.2314
C.4132
D.4123
C
T1
T2
T0
种群增长速率
2.下图表示某种鱼迁入某一生态系统后,种群数量的增长速率随时间的变化曲线,下列叙述正确的是(
)
B
在T0-T2时,种群数量呈“J”型增长
若在T2时种群的数量为N,则在T1时种群的数量为N/2;
捕获该鱼的最佳时期为T2时
在TI-T2时,该鱼种群数量呈下降趋势。
3、种群在理想环境中,呈“J”型曲线增长(如图中甲);在有环境阻力条件下,呈“S”型曲线增长(如图中乙)。下列有关种群增长曲线的叙述,正确的是(
)
A.若该图表示草履虫种群增长曲线,当种群数量达到e点后,增长速率为0
B.种群中出现环境阻力是在d点之后
C.若该图表示蝗虫种群增长曲线,则虫害的防治应在c点之后
D.K值是环境的最大容纳量,不随环境的变化而变化
A
第4章 种群和群落
第2节
种群数量的变化
大肠杆菌
一、建构种群增长模型
时间(min)
细胞数
0
20
40
60
80
100
1
2
4
8
16
32
种群数量的变化
在营养和生存空间没有限制的情况下,某种细菌每20分钟就通过分裂繁殖一代。
问题探讨:
讨论2:根据上表,写出n代细菌数量的计算公式:
讨论3:72小时后,由一个细菌分裂产生的细菌数量是多少?
讨论1:请你计算出一个细菌产生的后代在不同时间的数量:
时间分钟
20
40
60
80
100
120
140
160
180
细菌数量
2
4
8
16
32
64
128
256
512
问题探讨:
Nn
=
1×2n
n=
60min
72h/20min=216
Nn=2n
=2216
讨论4:请根据讨论1表中数据,绘出大肠杆菌种群的增长曲线
时间(min)
20
40
60
80
100
120
140
160
180
分裂次数
1
2
3
4
5
6
7
8
9
数量(个)
2
4
8
16
32
64
128
256
512
数学方程式:Nn=2n
更精确,但较抽象不够直观。
曲线图:
更直观地反映出种群数量的增长趋势,但没有数学公式精确。
数学模型法
100
200
300
400
500
0
细菌数量(个)
时间(min)
20
40
60
80
100
180
0
160
1、数学模型:
是用来描述一个系统或它的性质的数学形式。
2、数学模型建构的步骤
一、建构种群增长模型的方法
提出问题
作出假设
数学表达
检验或修正
细菌每20min分裂一次
在资源和空间无限多的环境中,细菌种群的增长不会受种群密度增加的影响
Nn=2n
,N代表细菌数量,n表示第几代
观察、统计细菌数量,对自己所建立的模型进行检验或修正
一、建构种群增长的数学模型
5、如果细菌的起始数量不是1个,而是N0
,增长倍数不是2,而是λ,那么繁殖t次以后的种群数量(Nt)又该如表示?
Nt=N0
λt
一、建构种群增长的数学模型
6、请计算细菌每20分钟的增长率?看有何特点?
增长率:r=(N后-N前)/N前×100%
增长率(r)稳定不变
一、建构种群增长的数学模型
7、增长率(r)和增长倍数(λ)之间是什么关系?
r
=
λ-
1
由于增长率(r)稳定不变,所以增长倍数(λ)也保持不变。
一、建构种群增长的数学模型
8、增长率(r)的曲线是怎样的?
增长率
时间
增长率的变化曲线
一、建构种群增长的数学模型
9、计算细菌每20分钟的增长速率?看有何特点?
增长速率:v=(N后-N前)/t
增长速率越来越快
10、能否从曲线上看出增长速率的变化?
一、建构种群增长的数学模型
11、细菌增长的曲线像什么字母?
J
类似细菌在理想条件下的种群增长曲线,称为“J”型曲线。
自然界确有类似的细菌在理想条件下种群数量增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线大致呈“J”型.
时
间
种群数量
二、种群增长的“J”型曲线
①产生条件:
理想状态——食物充足,空间不限,气候适宜,没有天敌等;
②增长特点:
持续增长——种群数量每年以一定的倍数增长,第二年是第一年的λ倍。
③量的计算:t年后种群的数量为
Nt
=
N0λt
注:N0为起始数量,t为时间,Nt表示t年后该种群的数量,λ为一年前种群数量的倍数。
④例:实验室条件下、外来物种入侵、外来物种入侵早期阶段。
指数增长
二、种群增长的“J”型曲线
N0
?
增长率=
末数-初数
初数
增长速率=
末数-初数
单位时间
5.“J”型增长的增长率和增长速率
二、种群增长的“J”型曲线
种群增长率
种群增长速率
(无单位)
“J”型增长能一直持续下去吗?
达尔文估计,一对象,如果保证食物和其他条件,在没有其他生物或天敌危害的情况下,740~750年后就可以繁殖成具有19000000个个体的巨大种群,但是这一现象并没有在自然界中发生。
环境阻力:
食物有限
空间有限
种内斗争
种间竞争
天敌捕食……
高斯对大草履虫种群研究的实验
高斯(Gause,1934)把5个大草履虫置于0.5mL的培养液中,每隔24小时统计一次数据,经过反复实验,结果如下:
时间(天)
0
1
2
3
4
5
6
种群数量(个)
5
20
137
319
369
375
375
K=375
在环境条件不受破坏的情况下,一定空间所能维持的种群的最大数量称为环境容纳量,又称为K值
三、种群增长的“S”型曲线
2.产生条件:
存在环境阻力
1.种群经过一定时间的增长后,数量趋于稳定的增长曲线,称为“S”型曲线.
①资源和空间有限;②种内斗争加剧;③天敌数量增加;④出生率下降,死亡率上升,最终达到平衡。(出生率等于死亡率)
3.特点:种群数量达到环境所允许的最大值(K值)后将停止增长,围绕K值上下波动;当生存环境改变时,K值也会相应改变。
三、种群增长的“S”型曲线
4.
“S”型曲线的特征:
该曲线的斜率变化是怎样的?说明了什么?
B
A
C
K/2
A
B
C
增长速率
曲线的斜率先增后减,说明种群数量的增长速率先增后减。
时间
三、种群增长的“S”型曲线
5.
“S”型曲线的特征:
有最大值,称为_______。
增长速率最大时,种群数量为______,
在K值时增长速率为_______。
K/2
0
B
A
C
K/2
A
B
C
增长速率
K值
时间
6.“S”型增长的增长率和增长速率
K/2
K
种群增长速率
A
B
C
D
K
K/2
②有害生物的防治:
(1)K值的应用
①野生生物资源保护:
减小环境阻力,增大K值。
(如:为防鼠害而封储粮食、清除生活垃圾、保护鼠的天敌等)
增大环境阻力,降低K值。
7.
K值
与
K/2
的应用
控制种群数量,严防达到K/2值处(若达K/2值处,可导致该有害生物成灾,如蝗虫的防控)
(2)K/2的应用
①资源开发与利用:
捕捞后数量要维持在
K/2
,保证最大持续捕捞量,因为在这个水平上种群增长速率最大。
②有害生物防治:
最大日捕捞量:种群数量达到最大值(K值)时捕捞
项目
“J”型曲线
“S”型曲线
曲线
模型
形成条件
增长率
有无K值
增长速率曲线
小结
资源无限的理想条件
资源有限的自然条件
不变
逐渐减小
无K值,持续增加
有K值,可在K值附近上下波动
代表环境阻力—其数量表示生存斗争中被淘汰的个体数。
食物不足、空间有限、种内斗争、天敌捕食、气候不适等
讨论
:图中阴影部分代表的什么?
大多数种群的数量总是在波动之中的,
东亚飞蝗种群数量的波动
四、种群数量的波动和下降
(1)影响种群数量变化的因素:
A.内部/直接因素:出生(死亡)率、迁入(出)率
B.自然/间接因素:空间、气候、食物、天敌、传染病、自然灾害等。
C.人为/重要因素:对野生生物的乱捕滥猎、对种群数量的人工控制
(2)种群数量变化的类型:增长,稳定,波动、下降等。
(3)影响结果:大多数种群的数量总是在波动之中,在不利条件之下,还会急剧下降,甚至灭亡。
课堂练习
1.建构种群增长数学模型的方法包括以下步骤(
)
提出合理的假设
对模型进行检验或修正
用适当的数学形式对事物的性质进行表达
观察研究对象,提出问题
A.1234
B.2314
C.4132
D.4123
C
T1
T2
T0
种群增长速率
2.下图表示某种鱼迁入某一生态系统后,种群数量的增长速率随时间的变化曲线,下列叙述正确的是(
)
B
在T0-T2时,种群数量呈“J”型增长
若在T2时种群的数量为N,则在T1时种群的数量为N/2;
捕获该鱼的最佳时期为T2时
在TI-T2时,该鱼种群数量呈下降趋势。
3、种群在理想环境中,呈“J”型曲线增长(如图中甲);在有环境阻力条件下,呈“S”型曲线增长(如图中乙)。下列有关种群增长曲线的叙述,正确的是(
)
A.若该图表示草履虫种群增长曲线,当种群数量达到e点后,增长速率为0
B.种群中出现环境阻力是在d点之后
C.若该图表示蝗虫种群增长曲线,则虫害的防治应在c点之后
D.K值是环境的最大容纳量,不随环境的变化而变化
A
同课章节目录
- 第1章 人体的内环境与稳态
- 第1节 细胞生活的环境
- 第2节 内环境稳态的重要性
- 第2章 动物和人体生命活动的调节
- 第1节 通过神经系统的调节
- 第2节 通过激素的调节
- 第3节 神经调节与体液调节的关系
- 第4节 免疫调节
- 第3章 植物的激素调节
- 第1节 植物生长素的发现
- 第2节 生长素的生理作用
- 第3节 其他植物激素
- 第4章 种群和群落
- 第1节 种群的特征
- 第2节 种群数量的变化
- 第3节 群落的结构
- 第4节 群落的演替
- 第5章 生态系统及其稳定性
- 第1节 生态系统的结构
- 第2节 生态系统的能量流动
- 第3节 生态系统的物质循环
- 第4节 生态系统的信息传递
- 第5节 生态系统的稳定性
- 第6章 生态环境的保护
- 第1节 人口增长对生态环境的影响
- 第2节 保护我们共同的家园
