2020-2021学年浙教新版九年级上册数学《第4章 相似三角形》单元测试卷(word版、含解析)
文档属性
| 名称 | 2020-2021学年浙教新版九年级上册数学《第4章 相似三角形》单元测试卷(word版、含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 395.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 17:47:13 | ||
图片预览


文档简介
2020-2021学年浙教新版九年级上册数学《第4章
相似三角形》单元测试卷
一.选择题
1.若a:b=3:2,且b2=ac,则b:c=( )
A.4:3
B.3:2
C.2:3
D.3:4
2.若,则的值为( )
A.
B.
C.
D.
3.四条线段a,b,c,d成比例,其中b=3cm,c=8cm,d=12cm,则a=( )
A.2cm
B.4cm
C.6cm
D.8cm
4.如图,直线a∥b∥c,AB=BC,若DF=9,则EF的长度为( )
A.9
B.5
C.4
D.3
5.如图,在△ABC中,DE∥AB,且=,则的值为( )
A.
B.
C.
D.
6.已知2x=3y,那么下列结论中不正确的是( )
A.
B.
C.
D.
7.若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A.1:2
B.2:1
C.1:4
D.4:1
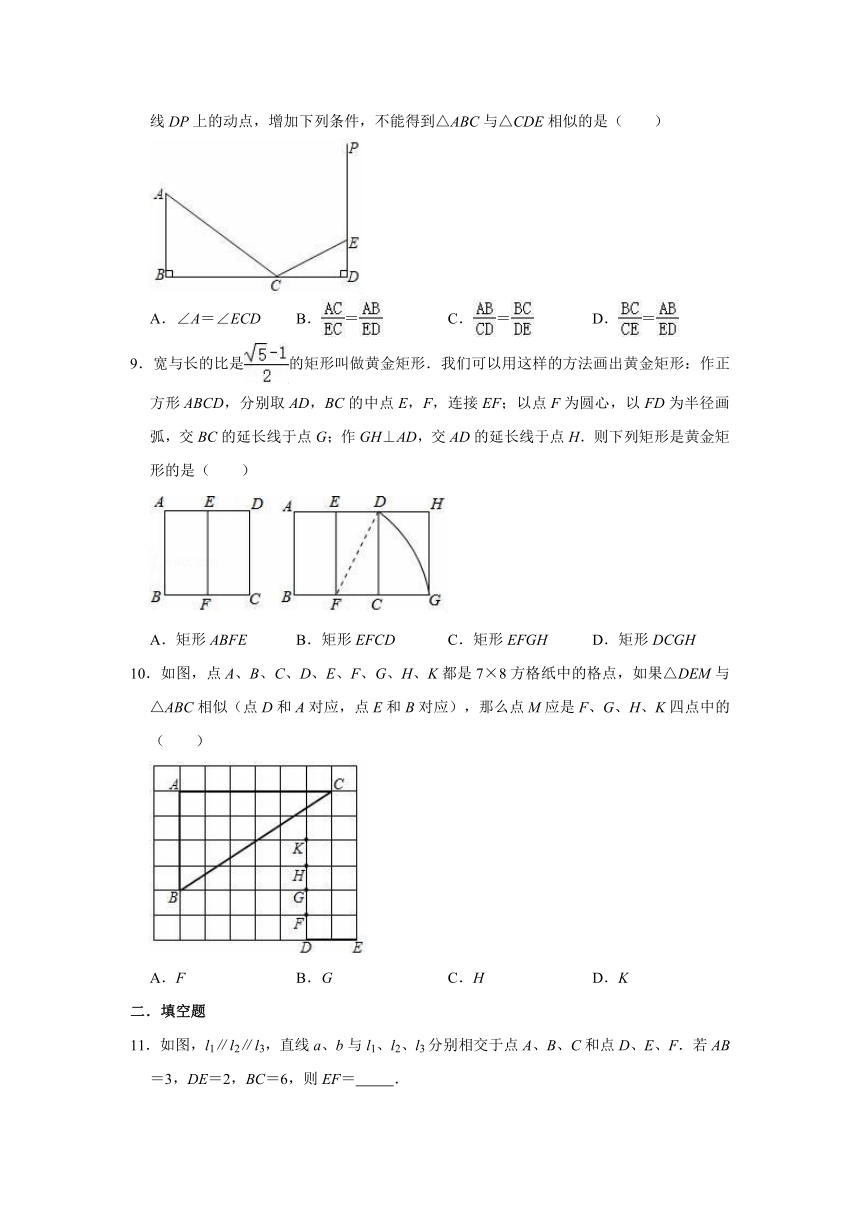
8.如图,AB⊥BD,PD⊥BD,垂足分别为点B,D,点C是线段BD上的动点,点E是射线DP上的动点,增加下列条件,不能得到△ABC与△CDE相似的是( )
A.∠A=∠ECD
B.=
C.=
D.=
9.宽与长的比是的矩形叫做黄金矩形.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD,BC的中点E,F,连接EF;以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H.则下列矩形是黄金矩形的是( )
A.矩形ABFE
B.矩形EFCD
C.矩形EFGH
D.矩形DCGH
10.如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,如果△DEM与△ABC相似(点D和A对应,点E和B对应),那么点M应是F、G、H、K四点中的( )
A.F
B.G
C.H
D.K
二.填空题
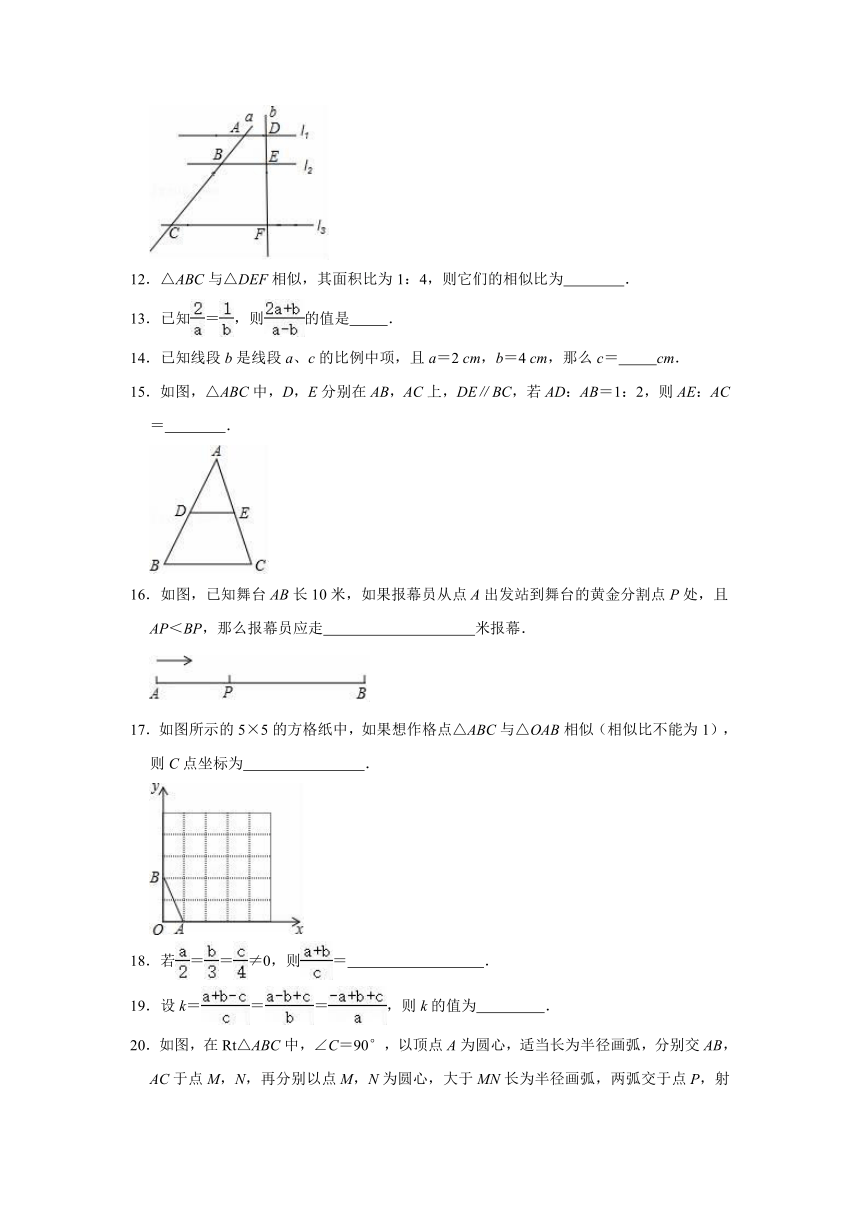
11.如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.若AB=3,DE=2,BC=6,则EF=
.
12.△ABC与△DEF相似,其面积比为1:4,则它们的相似比为
.
13.已知=,则的值是
.
14.已知线段b是线段a、c的比例中项,且a=2
cm,b=4
cm,那么c=
cm.
15.如图,△ABC中,D,E分别在AB,AC上,DE∥BC,若AD:AB=1:2,则AE:AC=
.
16.如图,已知舞台AB长10米,如果报幕员从点A出发站到舞台的黄金分割点P处,且AP<BP,那么报幕员应走
米报幕.
17.如图所示的5×5的方格纸中,如果想作格点△ABC与△OAB相似(相似比不能为1),则C点坐标为
.
18.若==≠0,则=
.
19.设k===,则k的值为
.
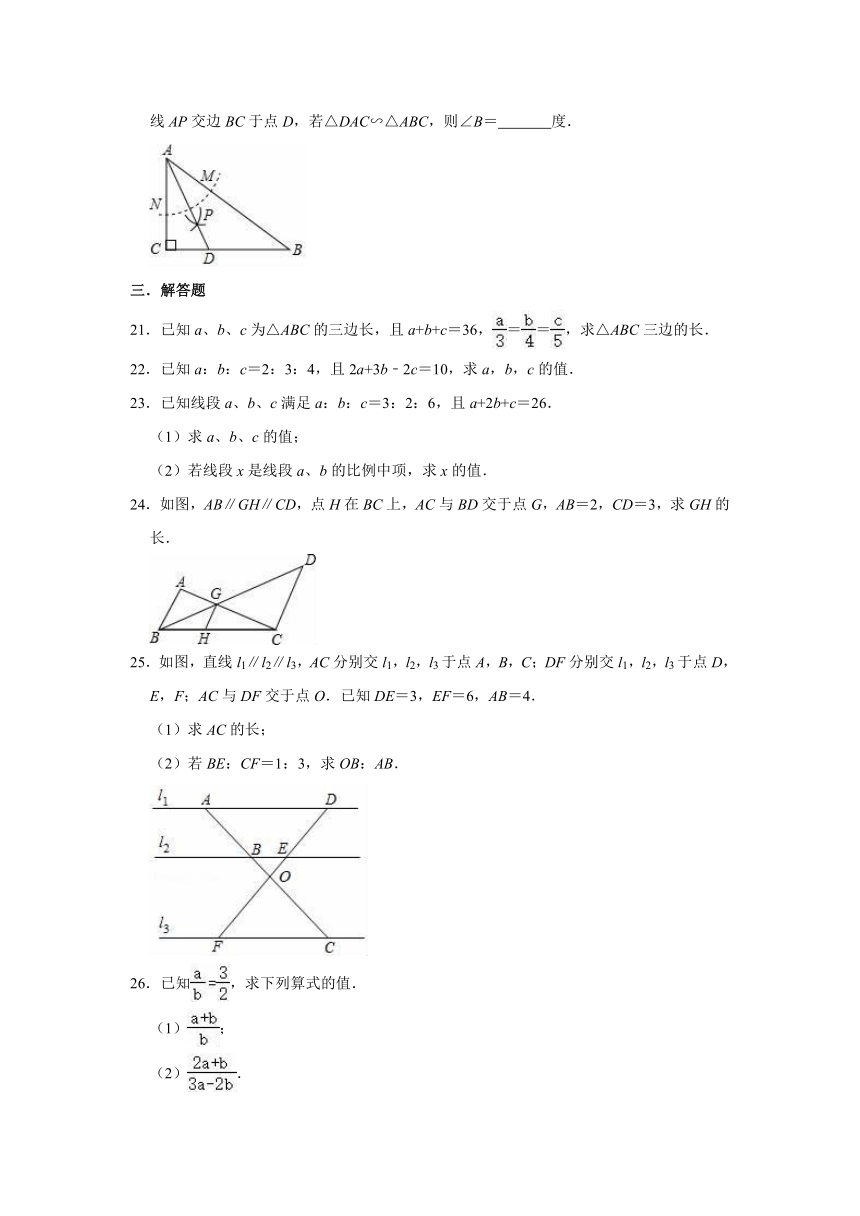
20.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,射线AP交边BC于点D,若△DAC∽△ABC,则∠B=
度.
三.解答题
21.已知a、b、c为△ABC的三边长,且a+b+c=36,==,求△ABC三边的长.
22.已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
23.已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
24.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,求GH的长.
25.如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
26.已知,求下列算式的值.
(1);
(2).
27.如图1,点C将线段AB分成两部分,如果,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.
(4)如图4,点E是平行四边形ABCD的边AB的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF是平行四边形ABCD的黄金分割线.请你画一条平行四边形ABCD的黄金分割线,使它不经过平行四边形ABCD各边黄金分割点.
参考答案与试题解析
一.选择题
1.解:∵b2=ac,
∴b:a=c:b,
∵a:b=3:2,
∴b:c=a:b=3:2.
故选:B.
2.解:因为,
所以b=,
把b=代入则=,
故选:B.
3.解:∵四条线段a、b、c、d成比例,
∴=,
∵b=3cm,c=8cm,d=12cm,
∴=,
解得:a=2cm.
故选:A.
4.解:∵直线a∥b∥c,
∴=,
∴DE=?EF=EF.
∵DF=DE+EF=EF+EF=9,
∴EF=5.
故选:B.
5.解:∵DE∥AB,
∴==,
故选:A.
6.解:A、∵=,∴2x=3y,故本选项正确;
B、∵=,∴2x=3y,故本选项正确;
C、∵=,∴3x=2y,故本选项错误;
D、∵=,∴2(x+y)=5y,解得2x=3y,故本选项正确.
故选:C.
7.解:∵两个相似三角形的面积之比为1:4,
∴它们的相似比为1:2,
∴它们的周长之比为1:2.
故选:A.
8.解:∵AB⊥BD,PD⊥BD,
∴∠ABC=∠CDE=90°,
A、∵∠A=∠ECD,∠ABC=∠CDE,
∴△ABC∽△EDC,
故A选项不合题意,
B、∵,
∴△ACB∽△ECD,
故B选项不合题意,
C、∵,∠ABC=∠CDE,
∴△ABC∽△CDE,
故C选项不合题意,
若,不能判定△ABC与△CDE相似,
故选:D.
9.解:设正方形的边长为2,则CD=2,CF=1
在直角三角形DCF中,DF=,
∴FG=,
∴CG=﹣1
∴,
∴矩形DCGH为黄金矩形
故选:D.
10.解:根据题意,
△DEM∽△ABC,AB=4,AC=6
DE=2,
∴DE:AB=DM:AC,
∴DM=3,
∴M应是H,
故选:C.
二.填空题
11.解:∵l1∥l2∥l3,
∴=,
又AB=3,DE=2,BC=6,
∴EF=4,
故答案为:4.
12.解:∵△ABC与△DEF相似,面积比为1:4,
∴它们的相似比为1:2,
故答案为:1:2.
13.解:∵=,
∴a=2b,
∴==5.
故答案为:5.
14.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积,
所以b2=ac,即42=2c,c=8.
故答案为:8.
15.解:∵DE∥BC,
∴AE:AC=AD:AB=1:2,
故答案为:1:2.
16.解:∵点P为AB的黄金分割点,AP<BP,
∴PB=AB=×10=5﹣5(米),
∴AP=AB﹣PB=10﹣(5﹣5)=15﹣5(米),
故答案为(15﹣5).
17.解:根据题意得:OA=1,OB=2,AB=,
∴当AB与AC对应时,有或者,
∴AC=或AC=5,
∵C在格点上,
∴AC=(不合题意),则AC=5,
∴C点坐标为(4,4),
同理当AB与BC对应时,可求得BC=或者BC=5,也是只有后者符合题意,此时C点坐标为(5,2)
∴C点坐标为(5,2)或(4,4).
故答案为:(4,4)或(5,2).
18.解:设===k≠0,
则a=2k,b=3k,c=4k,
所以==.
故答案是:.
19.解:当a+b+c≠0时,∵==,
∴====k==1
当a+b+c=0时,即a+b=﹣c,所以k===﹣2
所以k的值为1或﹣2.
20.解:由作图可知,AD平分∠CAB,
∴∠CAD=∠DAB,
∵△DAC∽△ABC,
∴∠CAD=∠B,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
∴3∠B=90°,
∴∠B=30°,
故答案为30.
三.解答题
21.解:==,得
a=c,b=c,
把a=c,b=c代入且a+b+c=36,得
c+c+c=36,
解得c=15,
a=c=9,
b=c=12,
△ABC三边的长:a=9,b=12,c=15.
22.解:设a=2k,b=3k,c=4k,
又∵2a+3b﹣2c=10,
∴4k+9k﹣8k=10,
5k=10,
解得k=2.
∴a=4,b=6,c=8.
23.解:(1)∵a:b:c=3:2:6,
∴设a=3k,b=2k,c=6k,
又∵a+2b+c=26,
∴3k+2×2k+6k=26,解得k=2,
∴a=6,b=4,c=12;
(2)∵x是a、b的比例中项,
∴x2=ab,
∴x2=4×6,
∴x=2或x=﹣2(舍去),
即x的值为.
24.解:∵AB∥CH∥CD,
∴△CGH∽△ABC,△BGH∽△BCD,
∴,,
∴+=+=1,
∵AB=2,CD=3,
∴=1,
∴GH=.
25.解:(1)∵l1∥l2∥l3,
∴,
即,
解得:AC=12;
(2)∵l1∥l2∥l3,
∴,
∵AB=4,AC=12,
∴BC=8,
∴OB=2,
∴.
26.解:(1)∵,
∴=;
(2)∵,
∴设a=3k,则b=2k,
∴===.
27.解:(1)直线CD是△ABC的黄金分割线.理由如下:
设△ABC的边AB上的高为h.
则,,,
∴,.
又∵点D为边AB的黄金分割点,
∴,
∴.
故直线CD是△ABC的黄金分割线.
(2)∵三角形的中线将三角形分成面积相等的两部分,
∴,即,
故三角形的中线不可能是该三角形的黄金分割线.
(3)∵DF∥CE,
∴△DFC和△DFE的公共边DF上的高也相等,
∴S△DFC=S△DFE,
∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF,S△BDC=S四边形BEFC.
又∵,
∴.
因此,直线EF也是△ABC的黄金分割线.(7分)
(4)画法不唯一,现提供两种画法;
画法一:如答图1,取EF的中点G,再过点G作一条直线分别交AB,DC于M,N点,则直线MN就是平行四边形ABCD的黄金分割线.
画法二:如答图2,在DF上取一点N,连接EN,再过点F作FM∥NE交AB于点M,连接MN,则直线MN就是平行四边形ABCD的黄金分割线.
(9分)
相似三角形》单元测试卷
一.选择题
1.若a:b=3:2,且b2=ac,则b:c=( )
A.4:3
B.3:2
C.2:3
D.3:4
2.若,则的值为( )
A.
B.
C.
D.
3.四条线段a,b,c,d成比例,其中b=3cm,c=8cm,d=12cm,则a=( )
A.2cm
B.4cm
C.6cm
D.8cm
4.如图,直线a∥b∥c,AB=BC,若DF=9,则EF的长度为( )
A.9
B.5
C.4
D.3
5.如图,在△ABC中,DE∥AB,且=,则的值为( )
A.
B.
C.
D.
6.已知2x=3y,那么下列结论中不正确的是( )
A.
B.
C.
D.
7.若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
A.1:2
B.2:1
C.1:4
D.4:1
8.如图,AB⊥BD,PD⊥BD,垂足分别为点B,D,点C是线段BD上的动点,点E是射线DP上的动点,增加下列条件,不能得到△ABC与△CDE相似的是( )
A.∠A=∠ECD
B.=
C.=
D.=
9.宽与长的比是的矩形叫做黄金矩形.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD,BC的中点E,F,连接EF;以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H.则下列矩形是黄金矩形的是( )
A.矩形ABFE
B.矩形EFCD
C.矩形EFGH
D.矩形DCGH
10.如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,如果△DEM与△ABC相似(点D和A对应,点E和B对应),那么点M应是F、G、H、K四点中的( )
A.F
B.G
C.H
D.K
二.填空题
11.如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别相交于点A、B、C和点D、E、F.若AB=3,DE=2,BC=6,则EF=
.
12.△ABC与△DEF相似,其面积比为1:4,则它们的相似比为
.
13.已知=,则的值是
.
14.已知线段b是线段a、c的比例中项,且a=2
cm,b=4
cm,那么c=
cm.
15.如图,△ABC中,D,E分别在AB,AC上,DE∥BC,若AD:AB=1:2,则AE:AC=
.
16.如图,已知舞台AB长10米,如果报幕员从点A出发站到舞台的黄金分割点P处,且AP<BP,那么报幕员应走
米报幕.
17.如图所示的5×5的方格纸中,如果想作格点△ABC与△OAB相似(相似比不能为1),则C点坐标为
.
18.若==≠0,则=
.
19.设k===,则k的值为
.
20.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,射线AP交边BC于点D,若△DAC∽△ABC,则∠B=
度.
三.解答题
21.已知a、b、c为△ABC的三边长,且a+b+c=36,==,求△ABC三边的长.
22.已知a:b:c=2:3:4,且2a+3b﹣2c=10,求a,b,c的值.
23.已知线段a、b、c满足a:b:c=3:2:6,且a+2b+c=26.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
24.如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,求GH的长.
25.如图,直线l1∥l2∥l3,AC分别交l1,l2,l3于点A,B,C;DF分别交l1,l2,l3于点D,E,F;AC与DF交于点O.已知DE=3,EF=6,AB=4.
(1)求AC的长;
(2)若BE:CF=1:3,求OB:AB.
26.已知,求下列算式的值.
(1);
(2).
27.如图1,点C将线段AB分成两部分,如果,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果,那么称直线l为该图形的黄金分割线.
(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.
(4)如图4,点E是平行四边形ABCD的边AB的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF是平行四边形ABCD的黄金分割线.请你画一条平行四边形ABCD的黄金分割线,使它不经过平行四边形ABCD各边黄金分割点.
参考答案与试题解析
一.选择题
1.解:∵b2=ac,
∴b:a=c:b,
∵a:b=3:2,
∴b:c=a:b=3:2.
故选:B.
2.解:因为,
所以b=,
把b=代入则=,
故选:B.
3.解:∵四条线段a、b、c、d成比例,
∴=,
∵b=3cm,c=8cm,d=12cm,
∴=,
解得:a=2cm.
故选:A.
4.解:∵直线a∥b∥c,
∴=,
∴DE=?EF=EF.
∵DF=DE+EF=EF+EF=9,
∴EF=5.
故选:B.
5.解:∵DE∥AB,
∴==,
故选:A.
6.解:A、∵=,∴2x=3y,故本选项正确;
B、∵=,∴2x=3y,故本选项正确;
C、∵=,∴3x=2y,故本选项错误;
D、∵=,∴2(x+y)=5y,解得2x=3y,故本选项正确.
故选:C.
7.解:∵两个相似三角形的面积之比为1:4,
∴它们的相似比为1:2,
∴它们的周长之比为1:2.
故选:A.
8.解:∵AB⊥BD,PD⊥BD,
∴∠ABC=∠CDE=90°,
A、∵∠A=∠ECD,∠ABC=∠CDE,
∴△ABC∽△EDC,
故A选项不合题意,
B、∵,
∴△ACB∽△ECD,
故B选项不合题意,
C、∵,∠ABC=∠CDE,
∴△ABC∽△CDE,
故C选项不合题意,
若,不能判定△ABC与△CDE相似,
故选:D.
9.解:设正方形的边长为2,则CD=2,CF=1
在直角三角形DCF中,DF=,
∴FG=,
∴CG=﹣1
∴,
∴矩形DCGH为黄金矩形
故选:D.
10.解:根据题意,
△DEM∽△ABC,AB=4,AC=6
DE=2,
∴DE:AB=DM:AC,
∴DM=3,
∴M应是H,
故选:C.
二.填空题
11.解:∵l1∥l2∥l3,
∴=,
又AB=3,DE=2,BC=6,
∴EF=4,
故答案为:4.
12.解:∵△ABC与△DEF相似,面积比为1:4,
∴它们的相似比为1:2,
故答案为:1:2.
13.解:∵=,
∴a=2b,
∴==5.
故答案为:5.
14.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积,
所以b2=ac,即42=2c,c=8.
故答案为:8.
15.解:∵DE∥BC,
∴AE:AC=AD:AB=1:2,
故答案为:1:2.
16.解:∵点P为AB的黄金分割点,AP<BP,
∴PB=AB=×10=5﹣5(米),
∴AP=AB﹣PB=10﹣(5﹣5)=15﹣5(米),
故答案为(15﹣5).
17.解:根据题意得:OA=1,OB=2,AB=,
∴当AB与AC对应时,有或者,
∴AC=或AC=5,
∵C在格点上,
∴AC=(不合题意),则AC=5,
∴C点坐标为(4,4),
同理当AB与BC对应时,可求得BC=或者BC=5,也是只有后者符合题意,此时C点坐标为(5,2)
∴C点坐标为(5,2)或(4,4).
故答案为:(4,4)或(5,2).
18.解:设===k≠0,
则a=2k,b=3k,c=4k,
所以==.
故答案是:.
19.解:当a+b+c≠0时,∵==,
∴====k==1
当a+b+c=0时,即a+b=﹣c,所以k===﹣2
所以k的值为1或﹣2.
20.解:由作图可知,AD平分∠CAB,
∴∠CAD=∠DAB,
∵△DAC∽△ABC,
∴∠CAD=∠B,
∴∠CAB=2∠B,
∵∠CAB+∠B=90°,
∴3∠B=90°,
∴∠B=30°,
故答案为30.
三.解答题
21.解:==,得
a=c,b=c,
把a=c,b=c代入且a+b+c=36,得
c+c+c=36,
解得c=15,
a=c=9,
b=c=12,
△ABC三边的长:a=9,b=12,c=15.
22.解:设a=2k,b=3k,c=4k,
又∵2a+3b﹣2c=10,
∴4k+9k﹣8k=10,
5k=10,
解得k=2.
∴a=4,b=6,c=8.
23.解:(1)∵a:b:c=3:2:6,
∴设a=3k,b=2k,c=6k,
又∵a+2b+c=26,
∴3k+2×2k+6k=26,解得k=2,
∴a=6,b=4,c=12;
(2)∵x是a、b的比例中项,
∴x2=ab,
∴x2=4×6,
∴x=2或x=﹣2(舍去),
即x的值为.
24.解:∵AB∥CH∥CD,
∴△CGH∽△ABC,△BGH∽△BCD,
∴,,
∴+=+=1,
∵AB=2,CD=3,
∴=1,
∴GH=.
25.解:(1)∵l1∥l2∥l3,
∴,
即,
解得:AC=12;
(2)∵l1∥l2∥l3,
∴,
∵AB=4,AC=12,
∴BC=8,
∴OB=2,
∴.
26.解:(1)∵,
∴=;
(2)∵,
∴设a=3k,则b=2k,
∴===.
27.解:(1)直线CD是△ABC的黄金分割线.理由如下:
设△ABC的边AB上的高为h.
则,,,
∴,.
又∵点D为边AB的黄金分割点,
∴,
∴.
故直线CD是△ABC的黄金分割线.
(2)∵三角形的中线将三角形分成面积相等的两部分,
∴,即,
故三角形的中线不可能是该三角形的黄金分割线.
(3)∵DF∥CE,
∴△DFC和△DFE的公共边DF上的高也相等,
∴S△DFC=S△DFE,
∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF,S△BDC=S四边形BEFC.
又∵,
∴.
因此,直线EF也是△ABC的黄金分割线.(7分)
(4)画法不唯一,现提供两种画法;
画法一:如答图1,取EF的中点G,再过点G作一条直线分别交AB,DC于M,N点,则直线MN就是平行四边形ABCD的黄金分割线.
画法二:如答图2,在DF上取一点N,连接EN,再过点F作FM∥NE交AB于点M,连接MN,则直线MN就是平行四边形ABCD的黄金分割线.
(9分)
同课章节目录
