2021—2022学年浙教版数学八年级上册第1章三角形的初步知识检测卷(word、含答案)
文档属性
| 名称 | 2021—2022学年浙教版数学八年级上册第1章三角形的初步知识检测卷(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 170.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 17:20:58 | ||
图片预览

文档简介
第1章 三角形的初步知识检测卷
一、选择题(每题2分,共20分)
1.下列图形中,能说明∠1>∠2的是( )
2.下列命题中,假命题的个数是( )
①若a为实数,则a2>0;②直角都相等;③三角形三内角之和等于180°;④在同一平面内,垂直于同一条直线的两条直线平行;⑤不相交的两条线段必平行.
A.1个
B.2个
C.3个
D.4个
3.一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
4.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,使A,C,E在同一条直线上(如图所示),可以证明△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长.在这里判定△ABC≌△EDC的条件是( )
A.ASA
B.SAS
C.SSS
D.以上答案均不正确
第4题图
第5题图
5.如图,在余料ABCD中,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=96°,则∠EBC的度数为( )
A.45°
B.42°
C.36°
D.30°
6.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.3
B.4
C.6
D.5
第6题图
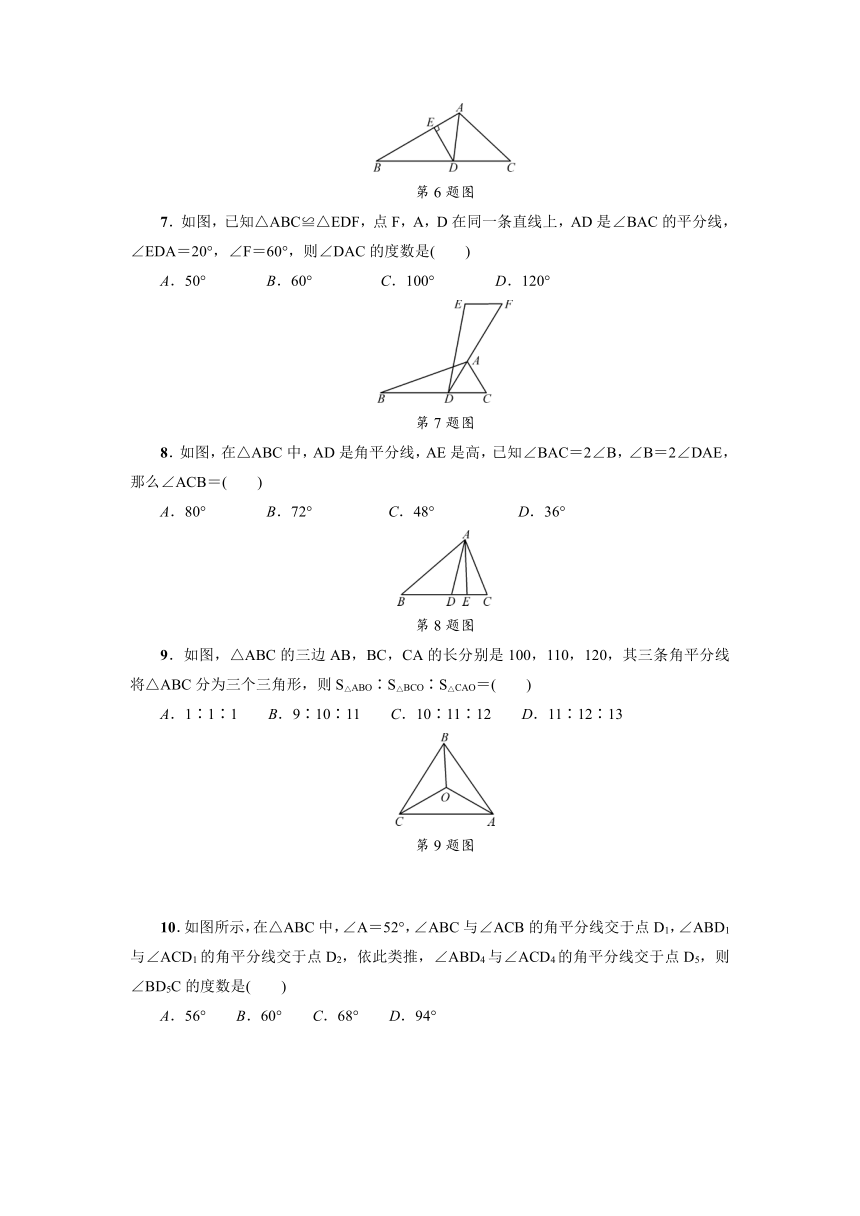
7.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
A.50°
B.60°
C.100°
D.120°
第7题图
8.如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B,∠B=2∠DAE,那么∠ACB=( )
A.80°
B.72°
C.48°
D.36°
第8题图
9.如图,△ABC的三边AB,BC,CA的长分别是100,110,120,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO=( )
A.1∶1∶1
B.9∶10∶11
C.10∶11∶12
D.11∶12∶13
第9题图
10.如图所示,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于点D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
A.56°
B.60°
C.68°
D.94°
第10题图
二、填空题(每题3分,共24分)
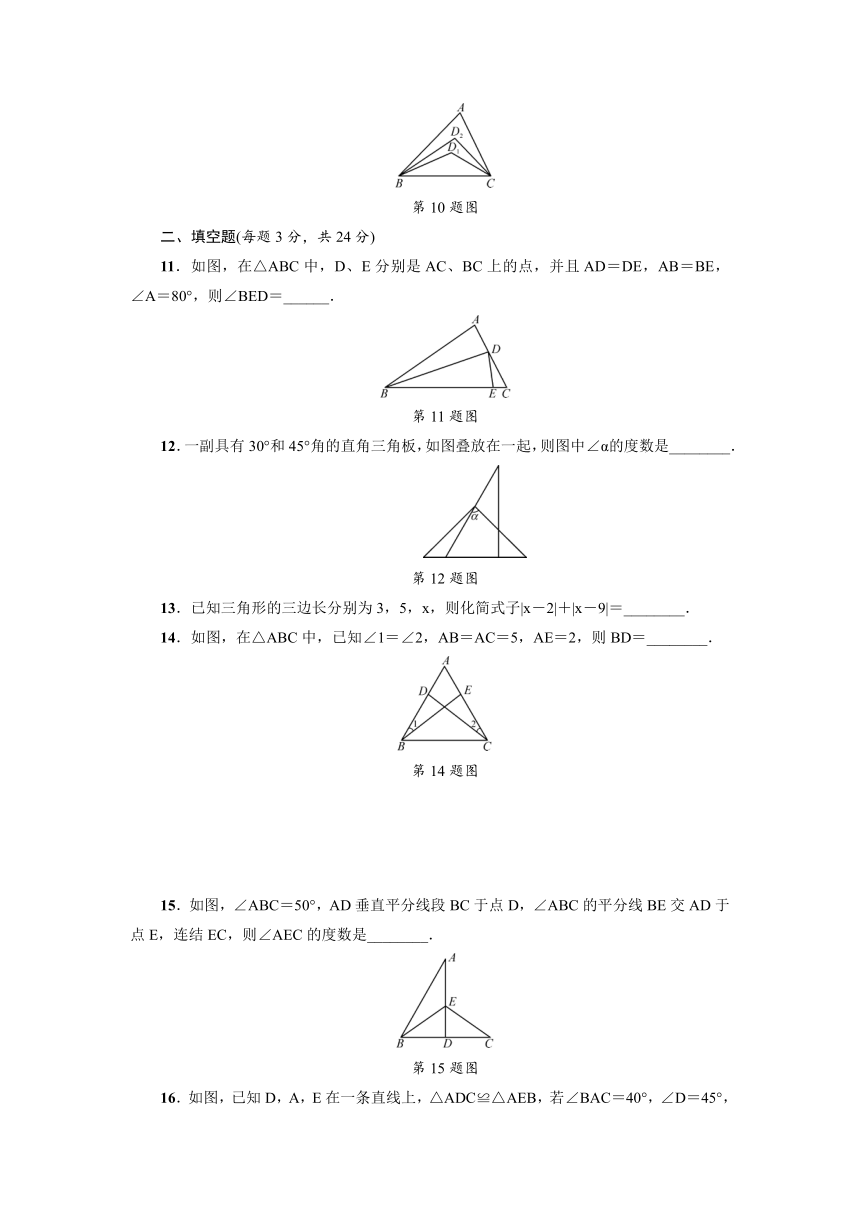
11.如图,在△ABC中,D、E分别是AC、BC上的点,并且AD=DE,AB=BE,∠A=80°,则∠BED=______.
第11题图
12.一副具有30°和45°角的直角三角板,如图叠放在一起,则图中∠α的度数是________.
第12题图
13.已知三角形的三边长分别为3,5,x,则化简式子|x-2|+|x-9|=________.
14.如图,在△ABC中,已知∠1=∠2,AB=AC=5,AE=2,则BD=________.
第14题图
15.如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连结EC,则∠AEC的度数是________.
第15题图
16.如图,已知D,A,E在一条直线上,△ADC≌△AEB,若∠BAC=40°,∠D=45°,则∠B的度数为________.
第16题图
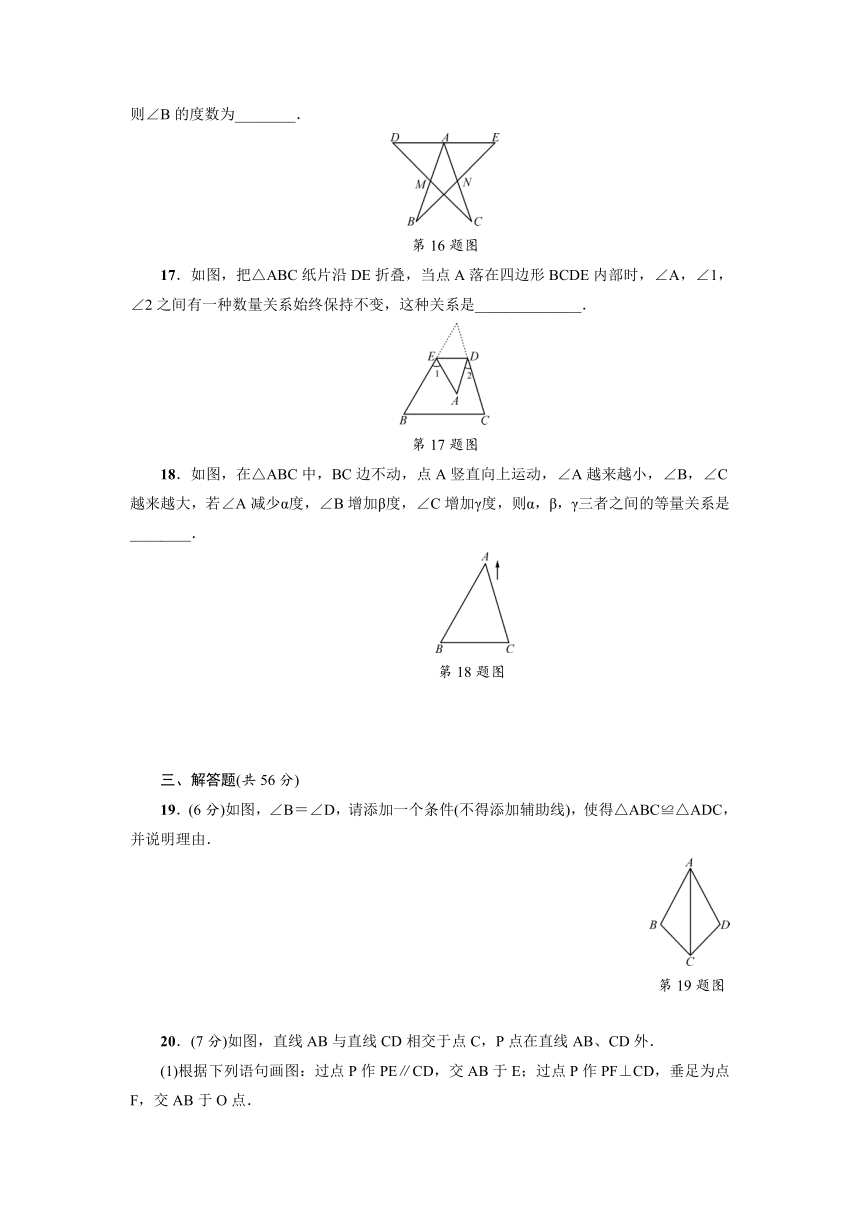
17.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A,∠1,∠2之间有一种数量关系始终保持不变,这种关系是______________.
第17题图
18.如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大,若∠A减少α度,∠B增加β度,∠C增加γ度,则α,β,γ三者之间的等量关系是________.
第18题图
三、解答题(共56分)
19.(6分)如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
第19题图
20.(7分)如图,直线AB与直线CD相交于点C,P点在直线AB、CD外.
(1)根据下列语句画图:过点P作PE∥CD,交AB于E;过点P作PF⊥CD,垂足为点F,交AB于O点.
(2)若∠DCB=130°,试求∠POE是多少度?并说明理由.
第20题图
21.(7分)(咸宁中考)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上.__________________________.
求证:________.
请你补全已知和求证,并写出证明过程.
第21题图
22.(8分)如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠1∶∠2∶∠3=28∶5∶3,求∠α的度数.
第22题图
23.(8分)(永州中考)如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E点,使DE=AB.
(1)求证:∠ABC=∠EDC.
(2)求证:△ABC≌△EDC.
第23题图
24.(10分)如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE.
(3)当直线MN绕点C旋转到图3的位置时,试问:DE,AD,BE具有怎样的等量关系?请直接写出这个等量关系.
第24题图
25.(10分)探索与发现:
如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样的图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的关系,并说明理由.
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经过点B,C,若∠A=50°,则∠ABX+∠ACX=________.
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数.
③如图4,∠ABD,∠ACD的10等分线相交于点G1,G2,…,G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.
第25题图
参考答案
一、选择题
1—5.DBBAB 6—10.AABCA
二、填空题
11.80°
12.75°
13.7
14.3
15.115°
16.25°
17.2∠A=∠1+∠2
18.α=β+γ
三、解答题
19.答案不唯一,理由略.
20.(1)如图. (2)∵PF⊥CD,∴∠PFC=90°,∵∠DCB=∠CFO+∠COF,∴∠COF=130°-90°=40°,∴∠POE=∠COF=40°.
第20题图
21.PD⊥OA,PE⊥OB,垂足分别为D、E PD=PE 证明:∵PD⊥OA,PE⊥OB,∴∠PDO=∠PEO=90°,在△PDO和△PEO中,∴△PDO≌△PEO(AAS),∴PD=PE.
22.∵∠1+∠2+∠3=180°,∠1∶∠2∶∠3=28∶5∶3,∴∠1=140°,∠2=25°,∠3=15°.设BE与CD的交点为F.∵△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,∴△ABE≌△ABC≌△ADC.∴∠2=∠ABE,∠3=∠ACD.∴∠FBC=2∠2=2×25°=50°,∠FCB=2∠3=2×15°=30°.∵∠α是△FBC的一个外角,∴∠α=∠FBC+∠FCB=50°+30°=80°.
23.(1)证明:在四边形ABCD中,∵∠A=∠BCD=90°,∴∠B+∠ADC=180°.又∵∠ADC+∠EDC=180°,∴∠ABC=∠EDC. (2)证明:连结AC.在△ABC和△EDC中,∵∴△ABC≌△EDC.
24.(1)∵∠ACB=90°,∴∠ACD+∠ECB=90°.∵AD⊥MN,BE⊥MN,∴∠ADC=∠BEC=90°,∴∠DAC+∠ACD=90°,∴∠DAC=∠ECB.在△ADC和△CEB中,∵∴△ADC≌△CEB(AAS),∴AD=CE,DC=EB.∵DE=CE+CD,∴DE=AD+BE.
(2)同(1)可证,∠DAC=∠ECB.又∵∠ADC=∠BEC=90°,AC=CB,∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE.∵DE=CE-CD,∴DE=AD-BE. (3)DE=BE-AD.
25.(1)连结AD并延长至点F,由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠CAD+∠C,∴∠BDF+∠CDF=∠BAD+∠CAD+∠B+∠C,即∠BDC=∠A+∠B+∠C. (2)①40° ②由(1)的结论得∠DBE=∠A+∠ADB+∠AEB,∴∠ADB+∠AEB=80°.∴∠DCE=(∠ADB+∠AEB)+∠A=40°+50°=90°.③∵∠BG1C=(∠ABD+∠ACD)+∠A,∠ABD+∠ACD=∠BDC-∠A,∴77°=(140°-∠A)+∠A,∴∠A=70°.
一、选择题(每题2分,共20分)
1.下列图形中,能说明∠1>∠2的是( )
2.下列命题中,假命题的个数是( )
①若a为实数,则a2>0;②直角都相等;③三角形三内角之和等于180°;④在同一平面内,垂直于同一条直线的两条直线平行;⑤不相交的两条线段必平行.
A.1个
B.2个
C.3个
D.4个
3.一个三角形三个内角的度数之比为2∶3∶5,这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
4.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再作出BF的垂线DE,使A,C,E在同一条直线上(如图所示),可以证明△ABC≌△EDC,得ED=AB,因此,测得DE的长就是AB的长.在这里判定△ABC≌△EDC的条件是( )
A.ASA
B.SAS
C.SSS
D.以上答案均不正确
第4题图
第5题图
5.如图,在余料ABCD中,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于GH长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.若∠A=96°,则∠EBC的度数为( )
A.45°
B.42°
C.36°
D.30°
6.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A.3
B.4
C.6
D.5
第6题图
7.如图,已知△ABC≌△EDF,点F,A,D在同一条直线上,AD是∠BAC的平分线,∠EDA=20°,∠F=60°,则∠DAC的度数是( )
A.50°
B.60°
C.100°
D.120°
第7题图
8.如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B,∠B=2∠DAE,那么∠ACB=( )
A.80°
B.72°
C.48°
D.36°
第8题图
9.如图,△ABC的三边AB,BC,CA的长分别是100,110,120,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO=( )
A.1∶1∶1
B.9∶10∶11
C.10∶11∶12
D.11∶12∶13
第9题图
10.如图所示,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于点D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
A.56°
B.60°
C.68°
D.94°
第10题图
二、填空题(每题3分,共24分)
11.如图,在△ABC中,D、E分别是AC、BC上的点,并且AD=DE,AB=BE,∠A=80°,则∠BED=______.
第11题图
12.一副具有30°和45°角的直角三角板,如图叠放在一起,则图中∠α的度数是________.
第12题图
13.已知三角形的三边长分别为3,5,x,则化简式子|x-2|+|x-9|=________.
14.如图,在△ABC中,已知∠1=∠2,AB=AC=5,AE=2,则BD=________.
第14题图
15.如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连结EC,则∠AEC的度数是________.
第15题图
16.如图,已知D,A,E在一条直线上,△ADC≌△AEB,若∠BAC=40°,∠D=45°,则∠B的度数为________.
第16题图
17.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,∠A,∠1,∠2之间有一种数量关系始终保持不变,这种关系是______________.
第17题图
18.如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大,若∠A减少α度,∠B增加β度,∠C增加γ度,则α,β,γ三者之间的等量关系是________.
第18题图
三、解答题(共56分)
19.(6分)如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC,并说明理由.
第19题图
20.(7分)如图,直线AB与直线CD相交于点C,P点在直线AB、CD外.
(1)根据下列语句画图:过点P作PE∥CD,交AB于E;过点P作PF⊥CD,垂足为点F,交AB于O点.
(2)若∠DCB=130°,试求∠POE是多少度?并说明理由.
第20题图
21.(7分)(咸宁中考)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上.__________________________.
求证:________.
请你补全已知和求证,并写出证明过程.
第21题图
22.(8分)如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠1∶∠2∶∠3=28∶5∶3,求∠α的度数.
第22题图
23.(8分)(永州中考)如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC,延长AD到E点,使DE=AB.
(1)求证:∠ABC=∠EDC.
(2)求证:△ABC≌△EDC.
第23题图
24.(10分)如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE.
(3)当直线MN绕点C旋转到图3的位置时,试问:DE,AD,BE具有怎样的等量关系?请直接写出这个等量关系.
第24题图
25.(10分)探索与发现:
如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样的图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”,试探究∠BDC与∠A,∠B,∠C之间的关系,并说明理由.
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经过点B,C,若∠A=50°,则∠ABX+∠ACX=________.
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,求∠DCE的度数.
③如图4,∠ABD,∠ACD的10等分线相交于点G1,G2,…,G9,若∠BDC=140°,∠BG1C=77°,求∠A的度数.
第25题图
参考答案
一、选择题
1—5.DBBAB 6—10.AABCA
二、填空题
11.80°
12.75°
13.7
14.3
15.115°
16.25°
17.2∠A=∠1+∠2
18.α=β+γ
三、解答题
19.答案不唯一,理由略.
20.(1)如图. (2)∵PF⊥CD,∴∠PFC=90°,∵∠DCB=∠CFO+∠COF,∴∠COF=130°-90°=40°,∴∠POE=∠COF=40°.
第20题图
21.PD⊥OA,PE⊥OB,垂足分别为D、E PD=PE 证明:∵PD⊥OA,PE⊥OB,∴∠PDO=∠PEO=90°,在△PDO和△PEO中,∴△PDO≌△PEO(AAS),∴PD=PE.
22.∵∠1+∠2+∠3=180°,∠1∶∠2∶∠3=28∶5∶3,∴∠1=140°,∠2=25°,∠3=15°.设BE与CD的交点为F.∵△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,∴△ABE≌△ABC≌△ADC.∴∠2=∠ABE,∠3=∠ACD.∴∠FBC=2∠2=2×25°=50°,∠FCB=2∠3=2×15°=30°.∵∠α是△FBC的一个外角,∴∠α=∠FBC+∠FCB=50°+30°=80°.
23.(1)证明:在四边形ABCD中,∵∠A=∠BCD=90°,∴∠B+∠ADC=180°.又∵∠ADC+∠EDC=180°,∴∠ABC=∠EDC. (2)证明:连结AC.在△ABC和△EDC中,∵∴△ABC≌△EDC.
24.(1)∵∠ACB=90°,∴∠ACD+∠ECB=90°.∵AD⊥MN,BE⊥MN,∴∠ADC=∠BEC=90°,∴∠DAC+∠ACD=90°,∴∠DAC=∠ECB.在△ADC和△CEB中,∵∴△ADC≌△CEB(AAS),∴AD=CE,DC=EB.∵DE=CE+CD,∴DE=AD+BE.
(2)同(1)可证,∠DAC=∠ECB.又∵∠ADC=∠BEC=90°,AC=CB,∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE.∵DE=CE-CD,∴DE=AD-BE. (3)DE=BE-AD.
25.(1)连结AD并延长至点F,由外角定理可得∠BDF=∠BAD+∠B,∠CDF=∠CAD+∠C,∴∠BDF+∠CDF=∠BAD+∠CAD+∠B+∠C,即∠BDC=∠A+∠B+∠C. (2)①40° ②由(1)的结论得∠DBE=∠A+∠ADB+∠AEB,∴∠ADB+∠AEB=80°.∴∠DCE=(∠ADB+∠AEB)+∠A=40°+50°=90°.③∵∠BG1C=(∠ABD+∠ACD)+∠A,∠ABD+∠ACD=∠BDC-∠A,∴77°=(140°-∠A)+∠A,∴∠A=70°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
