2021-2022学年浙教版数学九年级上册1.4二次函数的应用同步练习(woerd、含答案)
文档属性
| 名称 | 2021-2022学年浙教版数学九年级上册1.4二次函数的应用同步练习(woerd、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 381.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 17:24:27 | ||
图片预览


文档简介
1.4二次函数的应用
一、单选题
1.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10
B.20
C.30
D.10或30
2.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
3.小红把班级勤工助学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本、利和为y元,则y与x之间的函数关系式为(
)
A.y=500(x+1)2
B.y=x2+500
C.y=x2+500x
D.y=x2+5x
4.某产品进货单价为90元,按100元一件出售时能售出500件.若每件涨价1元,则销售量就减少10件.则该产品能获得的最大利润为( )
A.5000元
B.8000元
C.9000元
D.10000元
5.如图1,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是(
)
A.8cm2
B.16cm2
C.24cm2
D.32cm2
6.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A.
B.
C.
D.
7.定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度(单位:)与水平距离(单位:)近似满足函数关系(a≠0).下表记录了该同学将篮球投出后的与的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为(
)
x
(单位:m)
y
(单位:m)
3.05
A.
B.
C.
D.
8.下表所列为某商店薄利多销的情况,某商品原价为元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为元时,日销量为(
)件.
降价(元)
日销量(件)
A.1200
B.750
C.1110
D.1140
9.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于轴对称,
轴,,最低点
在轴上,高
,,则右轮廓所在抛物线的解析式为(
)
A.
B.
C.
D.
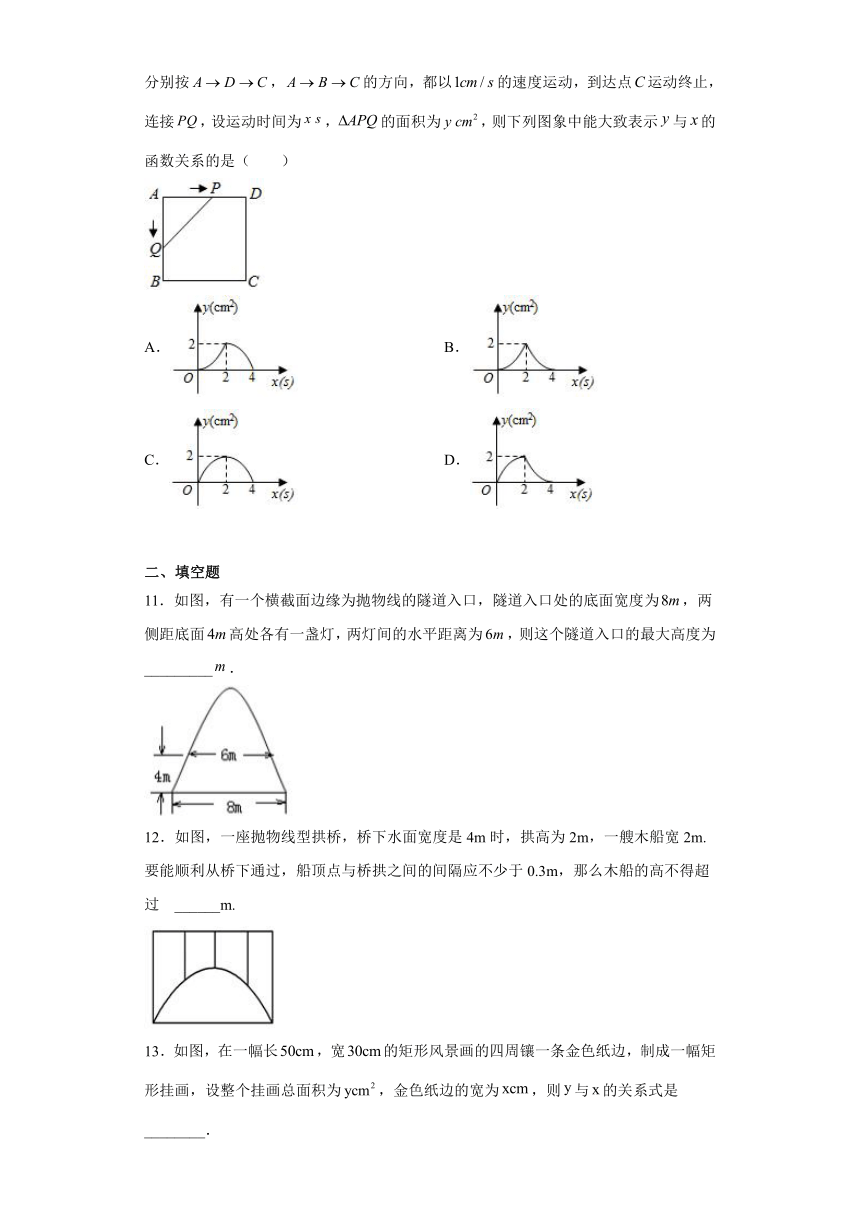
10.如图,正方形的边长为,动点,同时从点出发,在正方形的边上,分别按,的方向,都以的速度运动,到达点运动终止,连接,设运动时间为,的面积为,则下列图象中能大致表示与的函数关系的是( )
A.
B.
C.
D.
二、填空题
11.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为,两侧距底面高处各有一盏灯,两灯间的水平距离为,则这个隧道入口的最大高度为_________.
12.如图,一座抛物线型拱桥,桥下水面宽度是4m时,拱高为2m,一艘木船宽2m.要能顺利从桥下通过,船顶点与桥拱之间的间隔应不少于0.3m,那么木船的高不得超过
______m.
13.如图,在一幅长,宽的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂画,设整个挂画总面积为,金色纸边的宽为,则与的关系式是________.
14.如图,一位篮球运动员在距离篮圈中心水平距离处跳起投篮,球沿条抛物线运动,当球运动的水平距离为时,达到最大高度然后准确落入篮筐内.已知篮圈中心距离地面的高度为则这位运动员投跳时,球出手处距离地面的高度为______.
15.某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间(不包括A、B两点)经过时,将触发报警.现将A、B两点放置于平面直角坐标系中,(如图),已知点A、B的坐标分别为(0,4),(4,4),小车沿抛物线(<0)运动.若小车在运动过程中触发两次报警装置,则的取值范围是__________.
三、解答题
16.抛物线形桥拱的跨度为米,拱高为米,求桥拱的函数关系式.
17.在美化校园的活动中,某兴趣小组想在如图所示的直角墙角(两边足够长)用长的篱笆围成一个矩形花园(篱笆只围,两边),设,若在P处有一棵树与墙的距离分别是和,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.
18.小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”,小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图:
(1)如果在3月份出售这种植物,单株获利__________元;
(2)单株售价与月份x之间的关系式为___________;单株成本与月份x之间的关系式为__________.
(3)请你运用所学知识,帮助小哲的姑妈求出在哪个月销售这种“多肉植物”,单株获利最大(提示:单株获利=单株售价-单株成本).
参考答案
1.A
2.A
3.A
4.C
5.B
6.A
7.C
8.C
9.B
10.A
11.
12.1.2
13.
14.2.56
15.<<
16.(答案不唯一).
17.最大值是
18.(1)1;(2);;(3)5月份销售这种“多肉植物”,单株获利最大.
一、单选题
1.飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10
B.20
C.30
D.10或30
2.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
3.小红把班级勤工助学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本、利和为y元,则y与x之间的函数关系式为(
)
A.y=500(x+1)2
B.y=x2+500
C.y=x2+500x
D.y=x2+5x
4.某产品进货单价为90元,按100元一件出售时能售出500件.若每件涨价1元,则销售量就减少10件.则该产品能获得的最大利润为( )
A.5000元
B.8000元
C.9000元
D.10000元
5.如图1,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是(
)
A.8cm2
B.16cm2
C.24cm2
D.32cm2
6.一位运动员在距篮筐正下方水平距离处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为时,达到最大高度,然后准确落入篮筐.如图所示,建立平面直角坐标系,已知篮筐中心到地面的距离为,该运动员身高,在这次跳投中,球在头顶上方处出手,球出手时,他跳离地面的高度是( )
A.
B.
C.
D.
7.定点投篮是同学们喜爱的体育项目之一,某位同学投出篮球的飞行路线可以看作是抛物线的一部分,篮球飞行的竖直高度(单位:)与水平距离(单位:)近似满足函数关系(a≠0).下表记录了该同学将篮球投出后的与的三组数据,根据上述函数模型和数据,可推断出篮球飞行到最高点时,水平距离为(
)
x
(单位:m)
y
(单位:m)
3.05
A.
B.
C.
D.
8.下表所列为某商店薄利多销的情况,某商品原价为元,随着不同幅度的降价,日销量(单位为件)发生相应的变化.如果售价为元时,日销量为(
)件.
降价(元)
日销量(件)
A.1200
B.750
C.1110
D.1140
9.为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于轴对称,
轴,,最低点
在轴上,高
,,则右轮廓所在抛物线的解析式为(
)
A.
B.
C.
D.
10.如图,正方形的边长为,动点,同时从点出发,在正方形的边上,分别按,的方向,都以的速度运动,到达点运动终止,连接,设运动时间为,的面积为,则下列图象中能大致表示与的函数关系的是( )
A.
B.
C.
D.
二、填空题
11.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为,两侧距底面高处各有一盏灯,两灯间的水平距离为,则这个隧道入口的最大高度为_________.
12.如图,一座抛物线型拱桥,桥下水面宽度是4m时,拱高为2m,一艘木船宽2m.要能顺利从桥下通过,船顶点与桥拱之间的间隔应不少于0.3m,那么木船的高不得超过
______m.
13.如图,在一幅长,宽的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂画,设整个挂画总面积为,金色纸边的宽为,则与的关系式是________.
14.如图,一位篮球运动员在距离篮圈中心水平距离处跳起投篮,球沿条抛物线运动,当球运动的水平距离为时,达到最大高度然后准确落入篮筐内.已知篮圈中心距离地面的高度为则这位运动员投跳时,球出手处距离地面的高度为______.
15.某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间(不包括A、B两点)经过时,将触发报警.现将A、B两点放置于平面直角坐标系中,(如图),已知点A、B的坐标分别为(0,4),(4,4),小车沿抛物线(<0)运动.若小车在运动过程中触发两次报警装置,则的取值范围是__________.
三、解答题
16.抛物线形桥拱的跨度为米,拱高为米,求桥拱的函数关系式.
17.在美化校园的活动中,某兴趣小组想在如图所示的直角墙角(两边足够长)用长的篱笆围成一个矩形花园(篱笆只围,两边),设,若在P处有一棵树与墙的距离分别是和,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.
18.小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”,小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图:
(1)如果在3月份出售这种植物,单株获利__________元;
(2)单株售价与月份x之间的关系式为___________;单株成本与月份x之间的关系式为__________.
(3)请你运用所学知识,帮助小哲的姑妈求出在哪个月销售这种“多肉植物”,单株获利最大(提示:单株获利=单株售价-单株成本).
参考答案
1.A
2.A
3.A
4.C
5.B
6.A
7.C
8.C
9.B
10.A
11.
12.1.2
13.
14.2.56
15.<<
16.(答案不唯一).
17.最大值是
18.(1)1;(2);;(3)5月份销售这种“多肉植物”,单株获利最大.
同课章节目录
