2021-2022学年 浙教版九年级数学上册第一章 二次函数单元提高测试卷(word版、含解析)
文档属性
| 名称 | 2021-2022学年 浙教版九年级数学上册第一章 二次函数单元提高测试卷(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 528.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 17:55:52 | ||
图片预览



文档简介
浙教版九年级上册数学第一章《二次函数》综合测试
一.选择题(共10题,30分)
1.
将抛物线y=x2向上平移2个单位后,所得的抛物线的函数表达式为( )
A.y=x2+2
B.y=x2-2
C.y=(x+2)2
D.y=(x-2)2
2.
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
3.
将函数y=
x2﹣x化为y=a(x﹣m)2+k的形式,得(??????)
A.
y=
(x﹣1)2﹣
B.
y=
(x﹣
)2+
C.
y=
(x﹣1)2+
D.
y=
(x﹣
)2﹣
4.
抛物线y=ax
2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )
A.
b
2-4ac<0
B.
abc<0
C.
D.
a-b+c<0
5.
进价为80元的商品,按90元一个售出时,可卖出400个.已知
这种商品每个涨价1元,其销售量就减少20个,则获得利润最大时售价应为(
)
A.
90元
B.
95元
C.
100元
D.
105元
6.
对于二次函数y=(x-1)2+2的图象,下列说法正确的是()
A.开口向下
B.对称轴是x=-1
C.顶点坐标是(-1,2)
D.与x轴没有交点
7.
从地面竖直向上抛出一个小球,小球的高度h(m)与小球运动时间t(s)之间的函数关系式为
y=30t?5t2
,那么小球从抛出至回落到地面所需要的时间是(
)
A.6
s
B.4
s
C.3
s
D.2
s
如图,在平面直角坐标系中,二次函数y=ax
2+c(a≠0)的图象过正方形ABOC的三个
顶点A,B,C,则ac的值是__________.
A.-2
B.-1
C.
D.
9.
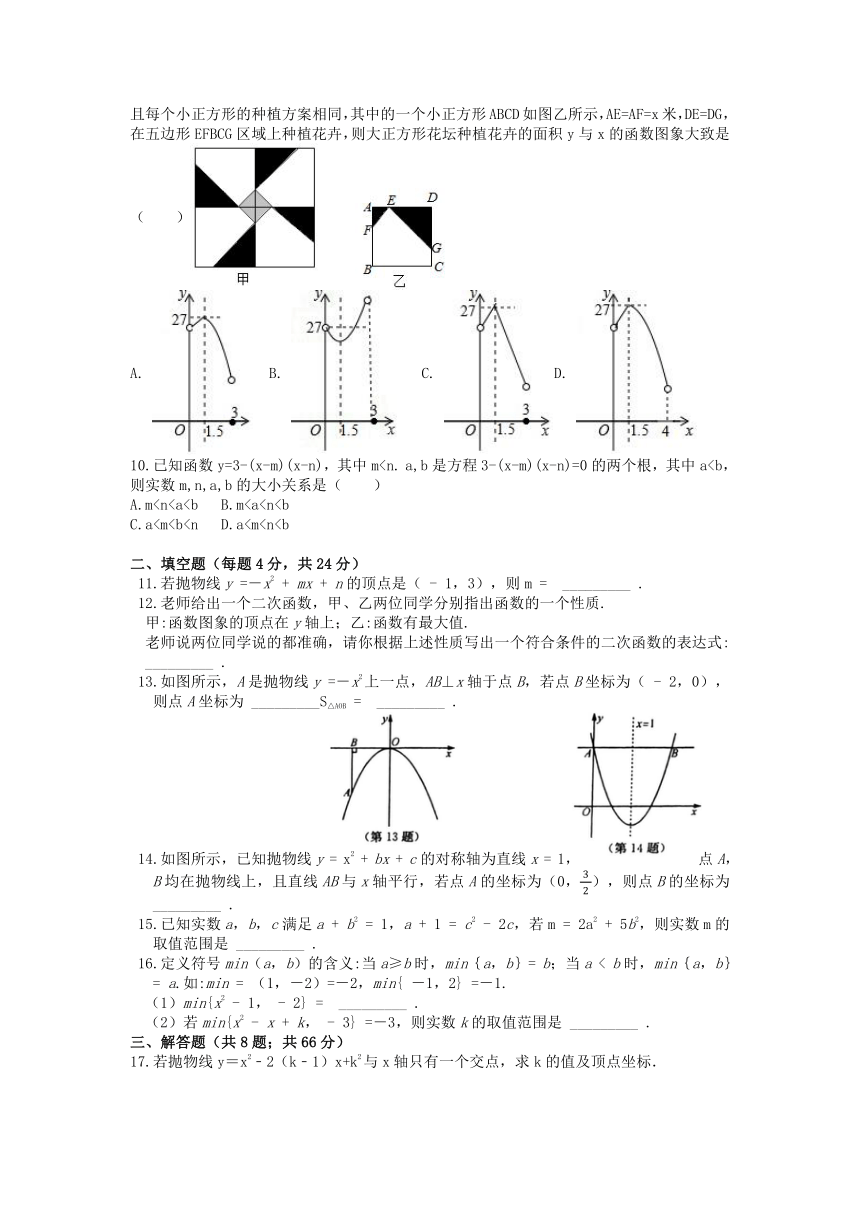
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同,其中的一个小正方形ABCD如图乙所示,AE=AF=x米,DE=DG,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
A.
B.
C.
D.
已知函数y=3-(x-m)(x-n),其中ma,b是方程3-(x-m)(x-n)=0的两个根,其中a)
mB.mC.aD.a二、填空题(每题4分,共24分)
11.若抛物线y
=-x2
+
mx
+
n的顶点是(
-
1,3),则m
=
_________
.
12.老师给出一个二次函数,甲、乙两位同学分别指出函数的一个性质.
甲:函数图象的顶点在y轴上;乙:函数有最大值.
老师说两位同学说的都准确,请你根据上述性质写出一个符合条件的二次函数的表达式:
_________
.
13.如图所示,A是抛物线y
=-x2上一点,AB⊥x轴于点B,若点B坐标为(
-
2,0),则点A坐标为
_________S△AOB
=
_________
.
14.如图所示,已知抛物线y
=
x2
+
bx
+
c的对称轴为直线x
=
1,点A,B均在抛物线上,且直线AB与x轴平行,若点A的坐标为(0,),则点B的坐标为
_________
.
15.已知实数a,b,c满足a
+
b2
=
1,a
+
1
=
c2
-
2c,若m
=
2a2
+
5b2,则实数m的取值范围是
_________
.
16.定义符号min(a,b)的含义:当a≥b时,min{a,b}=
b;当a
<
b时,min{a,b}=
a.如:min
=
(1,-2)=-2,min{
-1,2}
=-1.
(1)min{x2
-
1,
-
2}
=
_________
.
(2)若min{x2
-
x
+
k,
-
3}
=-3,则实数k的取值范围是
_________
.
三、解答题(共8题;共66分)
17.若抛物线y=x2﹣2(k﹣1)x+k2与x轴只有一个交点,求k的值及顶点坐标.
18.已知抛物线的顶点是(-2,3),且经过点(-1,4),求这条抛物线的函数表达式.
19.如图所示的正方形区域ABCD是某公园健身广场示意图,公园管理处想在其四个角的三角形区域内种植草皮加以绿化(阴影部分),剩余部分安装健身器材作为市民健身活动场所(四边形EFGH)其中AB=100米,且AE=AH=CF=CG.则当AE的长度为多少时,市民健身活动场所的面积达到最大?
20.已知二次函数y=﹣x2+6x﹣5.
(1)求二次函数图象的顶点坐标;
(2)当1≤x≤4时,函数的最大值和最小值分别为多少?
(3)当t≤x≤t+3时,函数的最大值为m
,
最小值为n
,
若m﹣n=3,求t的值.
21.今年以来,我市接待的游客人数逐月增加。据统计,游玩某景区的游客人数三月份为4万人,五月份为5.76万人。
(1)求四月和五月这两个月中,该景区游客人数平均每月增长百分之几;
(2)若该景区仅有A,B两个景点,售票处出示的三种购票方式如下表所示:
购票方式
甲
乙
丙
可游玩景点
A
B
A和B
门票价格
100元/人
80元/人
160元/人
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万,并且当甲、乙两种门票价格不变时,丙种门票每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票。
①若丙种门票下降10元,求景区六月份的门票总收入;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?
22.如图,已知抛物线L:y=x2+bx+c经过点A(0,﹣5),B(5,0).
(1)求b
,
c的值;
(2)连结AB
,
交抛物线L的对称轴于点M
.
①求点M的坐标;
②将抛物线L向左平移m(m>0)个单位得到抛物线L1.过点M作MN∥y轴,交抛物线L1于点N
.
P是抛物线L1上一点,横坐标为﹣1,过点P作PE∥x轴,交抛物线L于点E
,
点E在抛物线L对称轴的右侧.若PE+MN=10,求m的值.
23.综合与探究
如图,在平面直角坐标系中,抛物线
与
轴分别交于点
和点
(点
在点
的左侧),交
轴于点
.点
是线段
上的一个动点,沿
以每秒1个单位长度的速度由点
向点
运动,过点
作
轴,交抛物线于点
,交直线
于点
,连接
.
(1)求直线
的表达式;
(2)在点
运动过程中,运动时间
为何值时,
?
(3)在点
运动过程中,
的周长是否存在最小值?若存在,求出此时点
的坐标;若不存在,请说明理由.
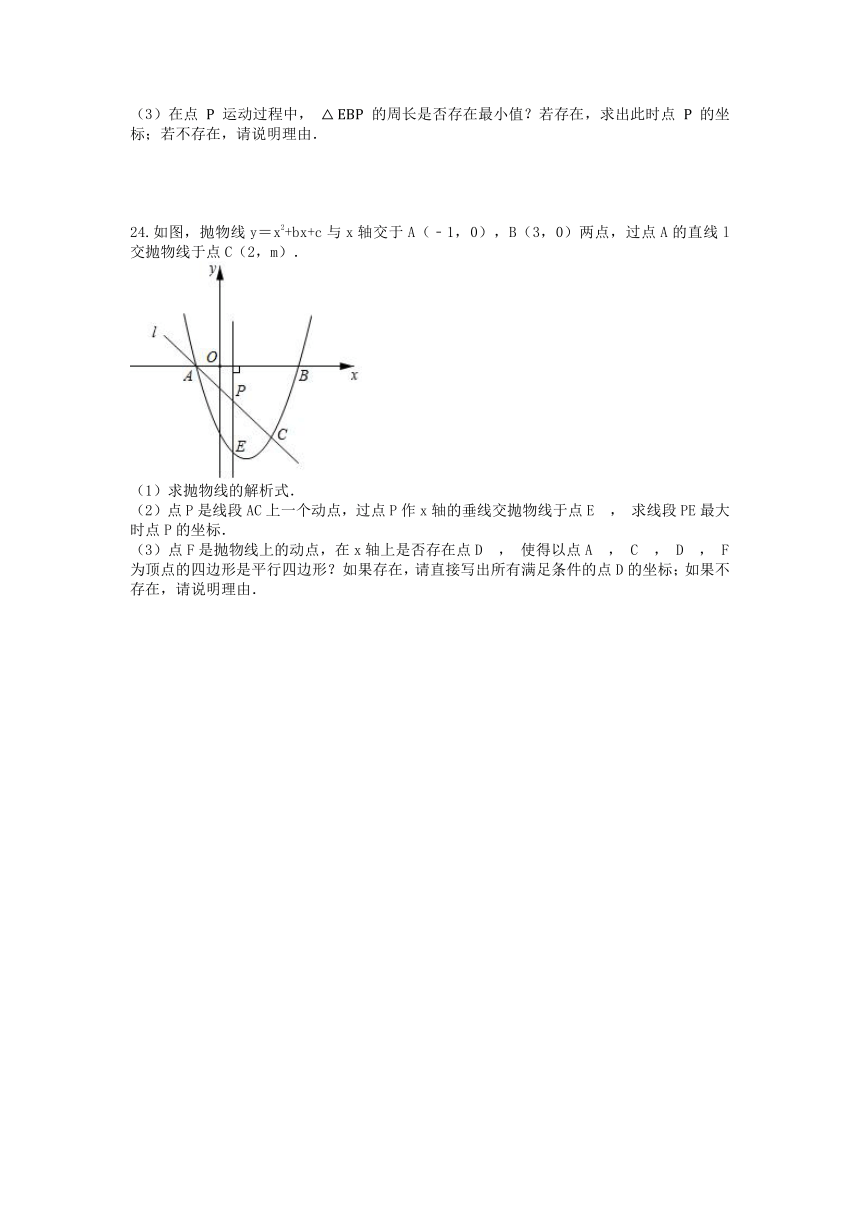
24.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).
(1)求抛物线的解析式.
(2)点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E
,
求线段PE最大时点P的坐标.
(3)点F是抛物线上的动点,在x轴上是否存在点D
,
使得以点A
,
C
,
D
,
F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
参考答案
一.选择题
1.
答案:A.
解:抛物线y=x2的顶点坐标为(0,0),
向上平移2个单位后的图象的顶点坐标为(0,2),
所以,所得图象的解析式为y=x2+2.
故选A.
2.
答案:A.
解:∵水在空中划出的曲线是抛物线y=-x2+4x的一部分,
∴水喷出的最大高度就是抛物线y=-x2+4x的顶点坐标的纵坐标.
∵y=-x2+4x=-(x-2)2+4,
∴此抛物线的顶点坐标为(2,4),
∴水喷出的最大高度为4米.
故选A.
3.
A
【解答】解:∵y=
x2﹣x
(x2﹣2x+1)﹣
=
(x﹣1)2﹣
,
故选A.
4.
C
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:由抛物线的开口向下知a<0,
与y轴的交点为在y轴的正半轴上,
∴c>0,
对称轴为y轴,即
<-1,
A,应为b
2-4ac>0,故本选项错误;
B,abc>0,故本选项错误;
C,即
<-1,故本选项正确;
D,x=-1时函数图象上的点在第二象限,所以a-b+c>0,故本选项错误.
故选C.
5.
答案:B
解答:解:设售价在90元的基础上涨x元
因为这种商品每个涨价1元,其销售量就减少20个,所以若涨x元,则销售量减少20x,按90元一个能全部售出,则按90+x元售出时,能售出400-20x个,每个的利润是90+x-80=10+x元
设总利润为y元,则y=(10+x)(400-20x)=-20x2+200x+4000,对称轴为x=5
所以x=5时,y有最大值,售价则为95元
所以售价定为每个95元时,利润最大.
故选B.
6.
答案:D.
解:由二次函数y=(x-1)2+2,可知:
函数图象开口向上,顶点坐标为(1,2),对称轴为直线x=1,抛物线与x轴没有公共点.
故选D.
7.
A
解:小球从抛出到落到地面运动的路径为0,即y=0
∴3t-5t?=0
解得:t1=0(舍去)
t2=6,
即小球从抛出到落到地面所有的时间是6秒.
应选A.故答案为:A
8.
答案:
A
【解答】解:设正方形的对角线OA长为2m,
则B(﹣m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:
c=2m①,am2+c=m②,
①代入②得:m2a+2m=m,解得:a=﹣
,
则ac=﹣
?2m=﹣2.
9.
【答案】
A
解:S△AEF=AE×AF=x2,S△DEG=DG×DE=(3-x)2=x2-3x+,
S五边形EFBCG=S正方形ABCD-S△AEF-S△DEG=9-x2-x2+3x-=-x2+3x+,
则y=-x2+3x+,∵AE<AD,
∴x<3,
综上可得:y=-x2+3x+,(0<x<3).
故选:A
10.
-【答案】
D
二,填空题
三、解答题
17.
解:∵抛物线y=x2﹣2(k﹣1)x+k2与x轴只有一个交点,
∴当y=0时,方程x2﹣2(k﹣1)x+k2=0有两个相等的实数根,
∴△=b2﹣4ac=[﹣2(k﹣1)]2﹣4k2=0,
解得:k=
.
当k=
时,该二次函数为:y=x2+x+
=(x+
)2
,
∴顶点坐标是(﹣
,0).
18.
解:∵抛物线的顶点是(-2,3),
∴抛物线解析式可设为
,???
把(-1,4)代入上式得
a(-1+2)2+3=4??????????????
解得a=1,??????
∴抛物线解析式为y=(x+2)2+3
19.
解:∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°.∵AE=AH=CF=CG,∴BE=BF=DG=DH,∴△AHE,△BEF,△CGF,△DCH都是等腰直角三角形;∴设AE=x米,则BE=(100-x)米.设四边形EFGH的面积为S,则S=100×100?2×
x2?2×
(100?x)2=-2x2+200x(0<x<100).
∵S=-2(x-50)2+5000.∵-2<0,当x=50时,S有最大值为5000.
答:当AE=50米时,市民健身活动场所的面积达到最大.
20.
(1)解:y=-x2
+6x-5=-(x-3)2+4,
∴顶点坐标为(3,4);
(2)解:∵顶点坐标为(3,
4),∴当x=3时,y最大
=4,
∵当1≤x≤3时,y随着x的增大而增大,当x=1时,y最小值=0,
:当3∴当1≤x≤4时,函数的最大值为4,最小值为0.
(3)解:当
t≤x≤t+3时,对t进行分类讨论,
①当t+3<3时,即t<0,y随着x的增大而增大,
当x=t+3时,m=-(t+3)
+6(t+3)-5=-t2+4,
当x=t时,n=-t2+6t-5,
∴m-n=-t2
+4-(-t2+6t-5)=-6t+9,
∴-6t+9=3,解得t=1
(不合题意,舍去);
②当0≤t<3时,顶点的横坐标在取值范围内,∴m=4,
ⅰ)当0≤t≤时,在x=t时,n=-t2+6t-5,
∴m-n=4-(-t2+6t-5)=t2-6t+9,
解得t1=3-
,
t2=3+(不合题意,舍去)
.
ⅱ)当n=-t2
+4,
m-n=4-(-t2
+4)=t2?,
∴t2?=3,解得t1=
,
t2=-
(不合题意,舍去)
;
③当t≥3时,y随着x的增大而减小,
当x=t时,m=-t2
+6t-5,
当x=t+3时,n=-(t+3)2
+6(t+3)-5=-t2
+4,
∴
m-n=-t2+6t-5-(-t2
+4)=6t-9,
∴6t-9=3,解得t=2
(不合题意,舍去),
综上所述,1=3-或.
21.
(1)解:解:该景区游客人数平均每月增长的百分率为x,根据题意得
4(1+x)2=5.76
解之:x1=20%,x2=-2.2(不符合题意,舍去).
答:该景区游客人数平均每月增长20%.
(2)解:①由题意得
(2-0.6)×100+(3-0.4)×80+(2+0.6+0.4)×(160-10)=140+208+450=798万.
答:若丙种门票下降10元,景区六月份的门票总收入为798万.
②设将丙种门票价格下降x元时,景区六月份的门票总收入为w元,根据题意得
w=100(2-0.06x)+80×(3-0.04x)+(160-x)(2+0.6x+0.4x)
整理得
w=-0.1x2+4.8x+760=-0.1(x-24)2+817.6
∵a=-0.1<0,
∴抛物线的开口向下,
∴当x=24时,w最大值=817.6万元.
答:将丙种门票价格下降24元时,景区六月份的门票总收入有最大值,最大值,817.6万元.
22.
(1)解:由题意得:
'
解之:
答:b,c的值分别为-4,-5.
(2)解:①设直线AB的解析式为y=kx+n(k≠0),
∵A(0,-5),B(5,0)
∴
解之:
∴直线AB的函数表达式为y=x-5.
∵y=x2-4x-5=(x-2)2-9
∴抛物线L的对称轴是直线x=2,
当x=2时,y=x-5=-3,
..点M的坐标是(2,-3);
②
∵将抛物线L向左平移m(m>0)个单位得到抛物线L1.
∴设抛物线L1的解析式为y=(x-2+m)-9,
∵MN/y轴,
.点N的坐标是(2,m2-9),
点P的横坐标为-1,
:.P点的坐标是(-1,m2-6m),?
设PE交抛物线L1于另一点Q,
.抛物线L1的对称轴是直线:x=2-m,PE∥x
∴点Q(5-2m,m2-6m)
当点N在点M的下方时
,
如图1,
∴PQ=5-2m-(-1)=6-2m,
MN=-3-(m2-9)=-m2+6
利用平移可知QE=m,
∴PE=6-2m+m=6-m,
∵PE+MN=10
∴6-m-m2+6=10
解之:m1=1,m2=-2(不符合题意,舍去);
当点N在点M的上方时,点Q在点P右侧,如图2,
PE=6-m,MN=m2-9+3=m2-6
∵PE+MN=10,
∴6-m+m2-6=10
解之:(舍去),(舍去),
当点N在点M的上方,点Q在点P的左侧时
m>3,
PE=6m,MN=m2-9+3=m2-6
∵PE+MN=10,
∴m+m2-6=10
解之:(舍去),
,
∴m的值为1或
23.
(1)解:∵抛物线
与
轴分别交于点
和点
,交
轴于点
,
∴当
时,
,即
,
当
时,
,
,
,即
,
,
设直线
的解析式为:
则
,
∴
,
∴直线
的表达式:
.
(2)解:∵点
沿
以每秒1个单位长度的速度由点
向点
运动,
∴
,
,
∵
轴,
∴
,
,
∴
∵
,
,
∴
,
,
∴△AOC是等腰直角三角形,
∴
,由勾股定理得:
,
∵
轴,
在
中,
,
∴△AEP也是等腰直角三角形,
∴
,
,
∴
,
∴当
时,即
或
时,
.
(3)解:在
中,
,
∴
,
∴
的周长:
.
∴当
最小时
的周长最小.
当
时,
最小,
∵
,
∴
,
在
中,
,
,
,
,
∴
,
∴
,
∴
.
24.(1)解:将A(﹣1,0),B(3,0)代入y=x2+bx+c,
得到
解得
,
∴y=x2﹣2x﹣3
(2)解:将C点的横坐标x=2代入y=x2﹣2x﹣3,得y=﹣3,∴C(2,﹣3);
∴直线AC的函数解析式是y=﹣x﹣1.
设P点的横坐标为x(﹣1≤x≤2),则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3);
∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2,
=﹣(x
)2
,
∵﹣1<0,
∴当x
时,PE的最大值
,此时P(
,
)
(3)解:存在.
理由:如图,设抛物线与y的交点为K,由题意K(0,﹣3),
∵C(2,﹣3),
∴CK∥x轴,CK=2,
当AC是平行四边形ACF1D1的边时,可得D1(﹣3,0).
当AC是平行四边形AF1CD2的对角线时,AD2=CK,可得D2(1,0),
当点F在x轴的上方时,令y=3,3=x2﹣2x﹣3,
解得x=1±
,
∴F3(1
,3),F4(1
,3),
由平移的性质可知D3(4
,0),D4(4
,0).
综上所述,满足条件的点D的坐标为(﹣3,0)或(1,0)或(4
,0)或(4
,0).
?
一.选择题(共10题,30分)
1.
将抛物线y=x2向上平移2个单位后,所得的抛物线的函数表达式为( )
A.y=x2+2
B.y=x2-2
C.y=(x+2)2
D.y=(x-2)2
2.
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
3.
将函数y=
x2﹣x化为y=a(x﹣m)2+k的形式,得(??????)
A.
y=
(x﹣1)2﹣
B.
y=
(x﹣
)2+
C.
y=
(x﹣1)2+
D.
y=
(x﹣
)2﹣
4.
抛物线y=ax
2+bx+c(a≠0)的图象如图所示,则下列说法正确的是( )
A.
b
2-4ac<0
B.
abc<0
C.
D.
a-b+c<0
5.
进价为80元的商品,按90元一个售出时,可卖出400个.已知
这种商品每个涨价1元,其销售量就减少20个,则获得利润最大时售价应为(
)
A.
90元
B.
95元
C.
100元
D.
105元
6.
对于二次函数y=(x-1)2+2的图象,下列说法正确的是()
A.开口向下
B.对称轴是x=-1
C.顶点坐标是(-1,2)
D.与x轴没有交点
7.
从地面竖直向上抛出一个小球,小球的高度h(m)与小球运动时间t(s)之间的函数关系式为
y=30t?5t2
,那么小球从抛出至回落到地面所需要的时间是(
)
A.6
s
B.4
s
C.3
s
D.2
s
如图,在平面直角坐标系中,二次函数y=ax
2+c(a≠0)的图象过正方形ABOC的三个
顶点A,B,C,则ac的值是__________.
A.-2
B.-1
C.
D.
9.
某校校园内有一个大正方形花坛,如图甲所示,它由四个边长为3米的小正方形组成,且每个小正方形的种植方案相同,其中的一个小正方形ABCD如图乙所示,AE=AF=x米,DE=DG,在五边形EFBCG区域上种植花卉,则大正方形花坛种植花卉的面积y与x的函数图象大致是( )
A.
B.
C.
D.
已知函数y=3-(x-m)(x-n),其中m
m
11.若抛物线y
=-x2
+
mx
+
n的顶点是(
-
1,3),则m
=
_________
.
12.老师给出一个二次函数,甲、乙两位同学分别指出函数的一个性质.
甲:函数图象的顶点在y轴上;乙:函数有最大值.
老师说两位同学说的都准确,请你根据上述性质写出一个符合条件的二次函数的表达式:
_________
.
13.如图所示,A是抛物线y
=-x2上一点,AB⊥x轴于点B,若点B坐标为(
-
2,0),则点A坐标为
_________S△AOB
=
_________
.
14.如图所示,已知抛物线y
=
x2
+
bx
+
c的对称轴为直线x
=
1,点A,B均在抛物线上,且直线AB与x轴平行,若点A的坐标为(0,),则点B的坐标为
_________
.
15.已知实数a,b,c满足a
+
b2
=
1,a
+
1
=
c2
-
2c,若m
=
2a2
+
5b2,则实数m的取值范围是
_________
.
16.定义符号min(a,b)的含义:当a≥b时,min{a,b}=
b;当a
<
b时,min{a,b}=
a.如:min
=
(1,-2)=-2,min{
-1,2}
=-1.
(1)min{x2
-
1,
-
2}
=
_________
.
(2)若min{x2
-
x
+
k,
-
3}
=-3,则实数k的取值范围是
_________
.
三、解答题(共8题;共66分)
17.若抛物线y=x2﹣2(k﹣1)x+k2与x轴只有一个交点,求k的值及顶点坐标.
18.已知抛物线的顶点是(-2,3),且经过点(-1,4),求这条抛物线的函数表达式.
19.如图所示的正方形区域ABCD是某公园健身广场示意图,公园管理处想在其四个角的三角形区域内种植草皮加以绿化(阴影部分),剩余部分安装健身器材作为市民健身活动场所(四边形EFGH)其中AB=100米,且AE=AH=CF=CG.则当AE的长度为多少时,市民健身活动场所的面积达到最大?
20.已知二次函数y=﹣x2+6x﹣5.
(1)求二次函数图象的顶点坐标;
(2)当1≤x≤4时,函数的最大值和最小值分别为多少?
(3)当t≤x≤t+3时,函数的最大值为m
,
最小值为n
,
若m﹣n=3,求t的值.
21.今年以来,我市接待的游客人数逐月增加。据统计,游玩某景区的游客人数三月份为4万人,五月份为5.76万人。
(1)求四月和五月这两个月中,该景区游客人数平均每月增长百分之几;
(2)若该景区仅有A,B两个景点,售票处出示的三种购票方式如下表所示:
购票方式
甲
乙
丙
可游玩景点
A
B
A和B
门票价格
100元/人
80元/人
160元/人
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万,并且当甲、乙两种门票价格不变时,丙种门票每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票。
①若丙种门票下降10元,求景区六月份的门票总收入;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?
22.如图,已知抛物线L:y=x2+bx+c经过点A(0,﹣5),B(5,0).
(1)求b
,
c的值;
(2)连结AB
,
交抛物线L的对称轴于点M
.
①求点M的坐标;
②将抛物线L向左平移m(m>0)个单位得到抛物线L1.过点M作MN∥y轴,交抛物线L1于点N
.
P是抛物线L1上一点,横坐标为﹣1,过点P作PE∥x轴,交抛物线L于点E
,
点E在抛物线L对称轴的右侧.若PE+MN=10,求m的值.
23.综合与探究
如图,在平面直角坐标系中,抛物线
与
轴分别交于点
和点
(点
在点
的左侧),交
轴于点
.点
是线段
上的一个动点,沿
以每秒1个单位长度的速度由点
向点
运动,过点
作
轴,交抛物线于点
,交直线
于点
,连接
.
(1)求直线
的表达式;
(2)在点
运动过程中,运动时间
为何值时,
?
(3)在点
运动过程中,
的周长是否存在最小值?若存在,求出此时点
的坐标;若不存在,请说明理由.
24.如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).
(1)求抛物线的解析式.
(2)点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E
,
求线段PE最大时点P的坐标.
(3)点F是抛物线上的动点,在x轴上是否存在点D
,
使得以点A
,
C
,
D
,
F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.
参考答案
一.选择题
1.
答案:A.
解:抛物线y=x2的顶点坐标为(0,0),
向上平移2个单位后的图象的顶点坐标为(0,2),
所以,所得图象的解析式为y=x2+2.
故选A.
2.
答案:A.
解:∵水在空中划出的曲线是抛物线y=-x2+4x的一部分,
∴水喷出的最大高度就是抛物线y=-x2+4x的顶点坐标的纵坐标.
∵y=-x2+4x=-(x-2)2+4,
∴此抛物线的顶点坐标为(2,4),
∴水喷出的最大高度为4米.
故选A.
3.
A
【解答】解:∵y=
x2﹣x
(x2﹣2x+1)﹣
=
(x﹣1)2﹣
,
故选A.
4.
C
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:由抛物线的开口向下知a<0,
与y轴的交点为在y轴的正半轴上,
∴c>0,
对称轴为y轴,即
<-1,
A,应为b
2-4ac>0,故本选项错误;
B,abc>0,故本选项错误;
C,即
<-1,故本选项正确;
D,x=-1时函数图象上的点在第二象限,所以a-b+c>0,故本选项错误.
故选C.
5.
答案:B
解答:解:设售价在90元的基础上涨x元
因为这种商品每个涨价1元,其销售量就减少20个,所以若涨x元,则销售量减少20x,按90元一个能全部售出,则按90+x元售出时,能售出400-20x个,每个的利润是90+x-80=10+x元
设总利润为y元,则y=(10+x)(400-20x)=-20x2+200x+4000,对称轴为x=5
所以x=5时,y有最大值,售价则为95元
所以售价定为每个95元时,利润最大.
故选B.
6.
答案:D.
解:由二次函数y=(x-1)2+2,可知:
函数图象开口向上,顶点坐标为(1,2),对称轴为直线x=1,抛物线与x轴没有公共点.
故选D.
7.
A
解:小球从抛出到落到地面运动的路径为0,即y=0
∴3t-5t?=0
解得:t1=0(舍去)
t2=6,
即小球从抛出到落到地面所有的时间是6秒.
应选A.故答案为:A
8.
答案:
A
【解答】解:设正方形的对角线OA长为2m,
则B(﹣m,m),C(m,m),A(0,2m);
把A,C的坐标代入解析式可得:
c=2m①,am2+c=m②,
①代入②得:m2a+2m=m,解得:a=﹣
,
则ac=﹣
?2m=﹣2.
9.
【答案】
A
解:S△AEF=AE×AF=x2,S△DEG=DG×DE=(3-x)2=x2-3x+,
S五边形EFBCG=S正方形ABCD-S△AEF-S△DEG=9-x2-x2+3x-=-x2+3x+,
则y=-x2+3x+,∵AE<AD,
∴x<3,
综上可得:y=-x2+3x+,(0<x<3).
故选:A
10.
-【答案】
D
二,填空题
三、解答题
17.
解:∵抛物线y=x2﹣2(k﹣1)x+k2与x轴只有一个交点,
∴当y=0时,方程x2﹣2(k﹣1)x+k2=0有两个相等的实数根,
∴△=b2﹣4ac=[﹣2(k﹣1)]2﹣4k2=0,
解得:k=
.
当k=
时,该二次函数为:y=x2+x+
=(x+
)2
,
∴顶点坐标是(﹣
,0).
18.
解:∵抛物线的顶点是(-2,3),
∴抛物线解析式可设为
,???
把(-1,4)代入上式得
a(-1+2)2+3=4??????????????
解得a=1,??????
∴抛物线解析式为y=(x+2)2+3
19.
解:∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°.∵AE=AH=CF=CG,∴BE=BF=DG=DH,∴△AHE,△BEF,△CGF,△DCH都是等腰直角三角形;∴设AE=x米,则BE=(100-x)米.设四边形EFGH的面积为S,则S=100×100?2×
x2?2×
(100?x)2=-2x2+200x(0<x<100).
∵S=-2(x-50)2+5000.∵-2<0,当x=50时,S有最大值为5000.
答:当AE=50米时,市民健身活动场所的面积达到最大.
20.
(1)解:y=-x2
+6x-5=-(x-3)2+4,
∴顶点坐标为(3,4);
(2)解:∵顶点坐标为(3,
4),∴当x=3时,y最大
=4,
∵当1≤x≤3时,y随着x的增大而增大,当x=1时,y最小值=0,
:当3
(3)解:当
t≤x≤t+3时,对t进行分类讨论,
①当t+3<3时,即t<0,y随着x的增大而增大,
当x=t+3时,m=-(t+3)
+6(t+3)-5=-t2+4,
当x=t时,n=-t2+6t-5,
∴m-n=-t2
+4-(-t2+6t-5)=-6t+9,
∴-6t+9=3,解得t=1
(不合题意,舍去);
②当0≤t<3时,顶点的横坐标在取值范围内,∴m=4,
ⅰ)当0≤t≤时,在x=t时,n=-t2+6t-5,
∴m-n=4-(-t2+6t-5)=t2-6t+9,
解得t1=3-
,
t2=3+(不合题意,舍去)
.
ⅱ)当
+4,
m-n=4-(-t2
+4)=t2?,
∴t2?=3,解得t1=
,
t2=-
(不合题意,舍去)
;
③当t≥3时,y随着x的增大而减小,
当x=t时,m=-t2
+6t-5,
当x=t+3时,n=-(t+3)2
+6(t+3)-5=-t2
+4,
∴
m-n=-t2+6t-5-(-t2
+4)=6t-9,
∴6t-9=3,解得t=2
(不合题意,舍去),
综上所述,1=3-或.
21.
(1)解:解:该景区游客人数平均每月增长的百分率为x,根据题意得
4(1+x)2=5.76
解之:x1=20%,x2=-2.2(不符合题意,舍去).
答:该景区游客人数平均每月增长20%.
(2)解:①由题意得
(2-0.6)×100+(3-0.4)×80+(2+0.6+0.4)×(160-10)=140+208+450=798万.
答:若丙种门票下降10元,景区六月份的门票总收入为798万.
②设将丙种门票价格下降x元时,景区六月份的门票总收入为w元,根据题意得
w=100(2-0.06x)+80×(3-0.04x)+(160-x)(2+0.6x+0.4x)
整理得
w=-0.1x2+4.8x+760=-0.1(x-24)2+817.6
∵a=-0.1<0,
∴抛物线的开口向下,
∴当x=24时,w最大值=817.6万元.
答:将丙种门票价格下降24元时,景区六月份的门票总收入有最大值,最大值,817.6万元.
22.
(1)解:由题意得:
'
解之:
答:b,c的值分别为-4,-5.
(2)解:①设直线AB的解析式为y=kx+n(k≠0),
∵A(0,-5),B(5,0)
∴
解之:
∴直线AB的函数表达式为y=x-5.
∵y=x2-4x-5=(x-2)2-9
∴抛物线L的对称轴是直线x=2,
当x=2时,y=x-5=-3,
..点M的坐标是(2,-3);
②
∵将抛物线L向左平移m(m>0)个单位得到抛物线L1.
∴设抛物线L1的解析式为y=(x-2+m)-9,
∵MN/y轴,
.点N的坐标是(2,m2-9),
点P的横坐标为-1,
:.P点的坐标是(-1,m2-6m),?
设PE交抛物线L1于另一点Q,
.抛物线L1的对称轴是直线:x=2-m,PE∥x
∴点Q(5-2m,m2-6m)
当点N在点M的下方时
,
如图1,
∴PQ=5-2m-(-1)=6-2m,
MN=-3-(m2-9)=-m2+6
利用平移可知QE=m,
∴PE=6-2m+m=6-m,
∵PE+MN=10
∴6-m-m2+6=10
解之:m1=1,m2=-2(不符合题意,舍去);
当点N在点M的上方时,点Q在点P右侧,如图2,
PE=6-m,MN=m2-9+3=m2-6
∵PE+MN=10,
∴6-m+m2-6=10
解之:(舍去),(舍去),
当点N在点M的上方,点Q在点P的左侧时
m>3,
PE=6m,MN=m2-9+3=m2-6
∵PE+MN=10,
∴m+m2-6=10
解之:(舍去),
,
∴m的值为1或
23.
(1)解:∵抛物线
与
轴分别交于点
和点
,交
轴于点
,
∴当
时,
,即
,
当
时,
,
,
,即
,
,
设直线
的解析式为:
则
,
∴
,
∴直线
的表达式:
.
(2)解:∵点
沿
以每秒1个单位长度的速度由点
向点
运动,
∴
,
,
∵
轴,
∴
,
,
∴
∵
,
,
∴
,
,
∴△AOC是等腰直角三角形,
∴
,由勾股定理得:
,
∵
轴,
在
中,
,
∴△AEP也是等腰直角三角形,
∴
,
,
∴
,
∴当
时,即
或
时,
.
(3)解:在
中,
,
∴
,
∴
的周长:
.
∴当
最小时
的周长最小.
当
时,
最小,
∵
,
∴
,
在
中,
,
,
,
,
∴
,
∴
,
∴
.
24.(1)解:将A(﹣1,0),B(3,0)代入y=x2+bx+c,
得到
解得
,
∴y=x2﹣2x﹣3
(2)解:将C点的横坐标x=2代入y=x2﹣2x﹣3,得y=﹣3,∴C(2,﹣3);
∴直线AC的函数解析式是y=﹣x﹣1.
设P点的横坐标为x(﹣1≤x≤2),则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3);
∵P点在E点的上方,PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2,
=﹣(x
)2
,
∵﹣1<0,
∴当x
时,PE的最大值
,此时P(
,
)
(3)解:存在.
理由:如图,设抛物线与y的交点为K,由题意K(0,﹣3),
∵C(2,﹣3),
∴CK∥x轴,CK=2,
当AC是平行四边形ACF1D1的边时,可得D1(﹣3,0).
当AC是平行四边形AF1CD2的对角线时,AD2=CK,可得D2(1,0),
当点F在x轴的上方时,令y=3,3=x2﹣2x﹣3,
解得x=1±
,
∴F3(1
,3),F4(1
,3),
由平移的性质可知D3(4
,0),D4(4
,0).
综上所述,满足条件的点D的坐标为(﹣3,0)或(1,0)或(4
,0)或(4
,0).
?
同课章节目录
