2021-2022学年浙教版八年级数学上册1.1 认识三角形 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册1.1 认识三角形 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 950.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 08:11:55 | ||
图片预览



文档简介
(共18张PPT)
形状似如山,稳定性能坚.
三竿首尾连,学问不简单.
三角形
1.1认识三角形(1)
打一图形名称(
)
什么样的图形是三角形呢?…
三角形
由
三条线段首尾顺次相接所组成的图形叫做三角形.
三角形的定义
你能动手画一个三角形吗?
不在同一条直线上的
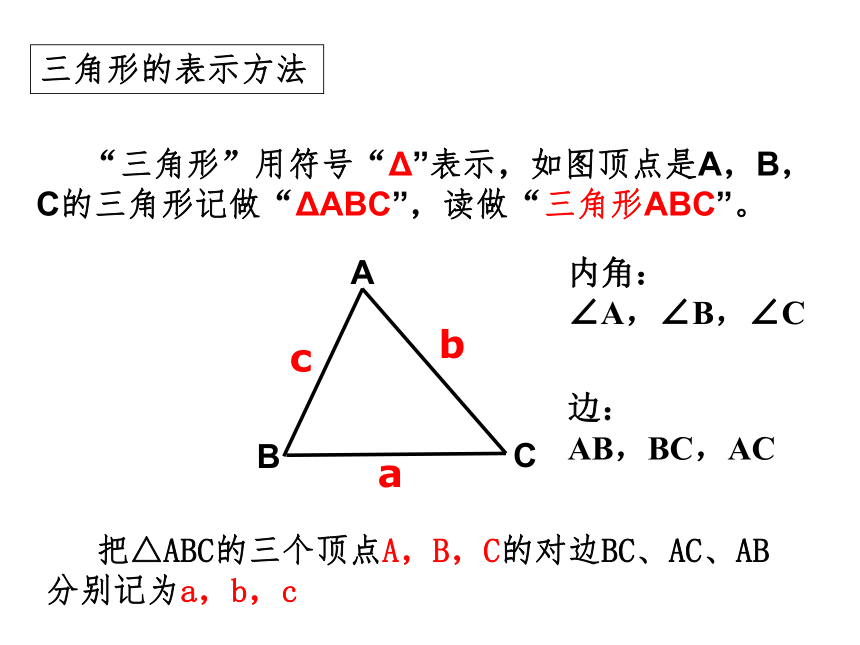
三角形的表示方法
A
B
C
“三角形”用符号“Δ”表示,如图顶点是A,B,C的三角形记做“ΔABC”,读做“三角形ABC”。
把△ABC的三个顶点A,B,C的对边BC、AC、AB分别记为a,b,c
a
b
c
内角:
∠A,∠B,∠C
边:
AB,BC,AC
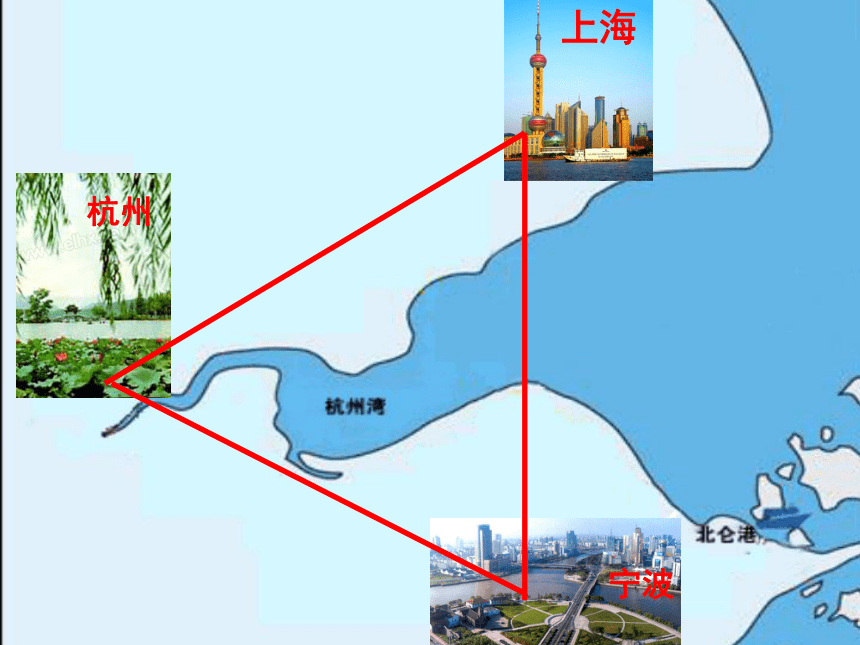
数学的美,生活中无处不在!
上海
宁波
杭州
上海
宁波
杭州
绍兴
杭州湾跨海大桥
嘉绍大桥
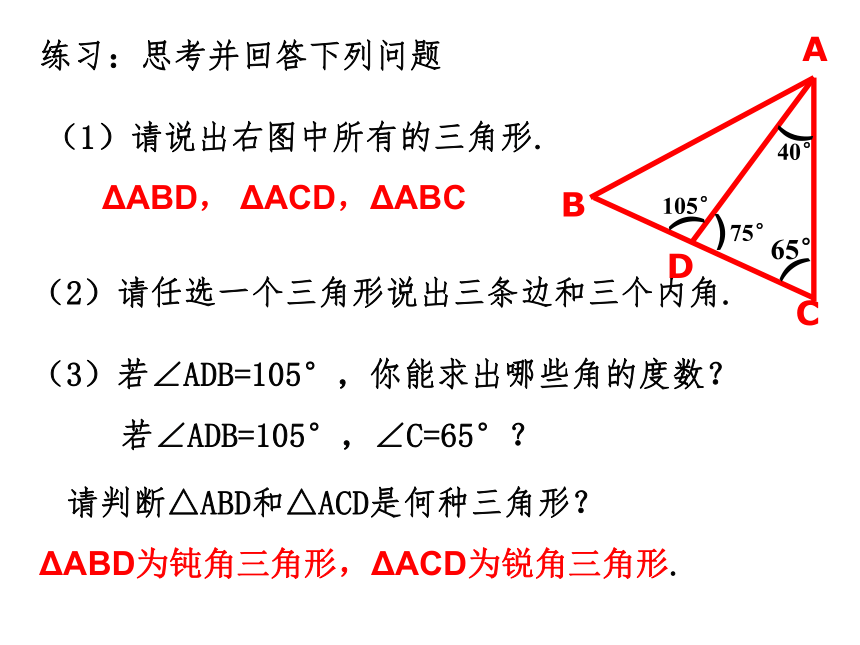
练习:思考并回答下列问题
(1)请说出右图中所有的三角形.
(2)请任选一个三角形说出三条边和三个内角.
ΔABD,
ΔACD,ΔABC
A
B
C
D
(3)若∠ADB=105°,你能求出哪些角的度数?
ΔABD为钝角三角形,ΔACD为锐角三角形.
若∠ADB=105°,∠C=65°?
请判断△ABD和△ACD是何种三角形?
(
105°
40°
(
75°
(
(
65°
三角形分类(根据角的大小)
三角形
锐角三角形
直角三角形
钝角三角形
三个角都是锐角
思考:一个三角形最多有几个锐角?
几个直角?
几个钝角?
有一个角是钝角
有一个角是直角
为什么宁波会建造一座跨海大桥,直接到上海,请用已学过的知识解释你的结论。
杭州湾跨海大桥
嘉绍大桥
两点之间
,线段最短
上海
宁波
杭州
绍兴
A
B
C
AB+BD>AD
AB+BC>AC
一般地,三角形的三条边有什么关系?
(杭州)
(上海)
(宁波)
A
B
D
(绍兴)
(杭州)
(上海)
三角形的性质(三角形的三边关系)
三角形的
两边之和大于第三边
b
c
a
A
B
C
a+b>c
b+c>a
c+a>b
任何
长度为6cm,
4cm,
3cm三条线段首尾相接能否组成三角形?
解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形
解:
∵最长线段是6cm
4+3>6
∴能组成三角形
判断方法:
如果三条线段长已知,只要先找出最长的线段,如果较小的两条线段之和大于最长线段,便可构成三角形;若不满足,则不能构成三角形.
应用与探究
现在要做一个三角形的铁架子,已有两根长分别为20cm和40cm的铁条,需要再找一根铁条,把它们首尾相接焊在一起.
C
40cm
20cm
xcm
A
B
AC-AB<X
AC+AB>X
即大于20cm,小于60cm
三角形任何两边的差与第三边关系?
你能提供一个选择的范围吗?
现有长分别10cm,30cm,40cm,50cm,60cm
的五根铁条,你会选择哪一条?
变式拓展
三角形任何两边的差与第三边关系:
b
c
a
A
B
C
三角形任何两边的差小于第三边。
若三角形的两边长分别为a和b,(设a?b)则第三边c与这两条边的关系:
a-b<c<a+b
三角形的性质(三角形的三边关系)
在ΔABC中,AB=7
BC=3,并且AC为奇数,那么ΔABC的周长为____________
15,17,19
当堂检测
2、由
的三条线段
所组成的图形叫做三角形
3、若a、b、c是△ABC的三条边,化简:
|a-b-c|+|a+b-c︳
不在同一直线上
首尾顺次相接
|a-b-c|+|a+b-c︳
=b+c-a+a+b-c
=2b
1、下列说法中错误的是(
)
A.有一个角是锐角的三角形是锐角三角形
B.三角形的三个内角中至少有两个角是锐角
C.一个三角形的三个内角中至少有一个内角
60°
D.如果三角形的两个内角之和小于90°,那么这个三角形是钝角三角形
A
4、如图所示,在△ABC中,D是BA上一点,则AB+2CD>AC+BC成立吗?
说明理由.
AB+2CD>AC+BC成立,理由如下:
∵在△ADC中,AD+CD>AC,在△BCD中,BD+CD>BC,
∴(AD+BD)+2CD>AC+BC,
即AB+2CD>AC+BC.
两个关系:
多个概念:
三角形(边,内角,分类…)
三角形的三边关系:
三角形任何两边的和大于第三边.
三角形任何两边的差小于第三边.
三角形日记
∴
两边之差?第三边?两边之和
一个方法:
判断三条已知线段能否组成三角形:
满足较短的两条线段之和大于最长的一条线段,则能组成三角形;若不满足,则不能组成三角形.
若三角形的周长为13,且三边长都是正整数,那么满足条件的三角形有多少个?
巩固思考
结束寄语:
大家的学习过程就像人生中的一个三角形支架,要以学、习、悟作为支架的三边,缺一不可,有了它的支撑,我们才能更加稳固的实现自己的人生目标!
形状似如山,稳定性能坚.
三竿首尾连,学问不简单.
三角形
1.1认识三角形(1)
打一图形名称(
)
什么样的图形是三角形呢?…
三角形
由
三条线段首尾顺次相接所组成的图形叫做三角形.
三角形的定义
你能动手画一个三角形吗?
不在同一条直线上的
三角形的表示方法
A
B
C
“三角形”用符号“Δ”表示,如图顶点是A,B,C的三角形记做“ΔABC”,读做“三角形ABC”。
把△ABC的三个顶点A,B,C的对边BC、AC、AB分别记为a,b,c
a
b
c
内角:
∠A,∠B,∠C
边:
AB,BC,AC
数学的美,生活中无处不在!
上海
宁波
杭州
上海
宁波
杭州
绍兴
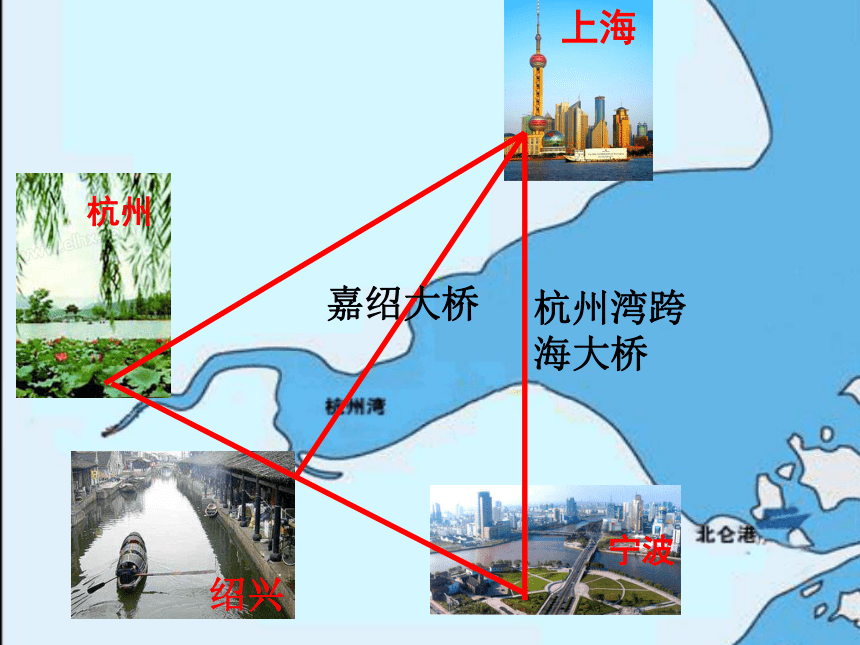
杭州湾跨海大桥
嘉绍大桥
练习:思考并回答下列问题
(1)请说出右图中所有的三角形.
(2)请任选一个三角形说出三条边和三个内角.
ΔABD,
ΔACD,ΔABC
A
B
C
D
(3)若∠ADB=105°,你能求出哪些角的度数?
ΔABD为钝角三角形,ΔACD为锐角三角形.
若∠ADB=105°,∠C=65°?
请判断△ABD和△ACD是何种三角形?
(
105°
40°
(
75°
(
(
65°
三角形分类(根据角的大小)
三角形
锐角三角形
直角三角形
钝角三角形
三个角都是锐角
思考:一个三角形最多有几个锐角?
几个直角?
几个钝角?
有一个角是钝角
有一个角是直角
为什么宁波会建造一座跨海大桥,直接到上海,请用已学过的知识解释你的结论。
杭州湾跨海大桥
嘉绍大桥
两点之间
,线段最短
上海
宁波
杭州
绍兴
A
B
C
AB+BD>AD
AB+BC>AC
一般地,三角形的三条边有什么关系?
(杭州)
(上海)
(宁波)
A
B
D
(绍兴)
(杭州)
(上海)
三角形的性质(三角形的三边关系)
三角形的
两边之和大于第三边
b
c
a
A
B
C
a+b>c
b+c>a
c+a>b
任何
长度为6cm,
4cm,
3cm三条线段首尾相接能否组成三角形?
解:∵6+4>3
6+3>4
4+3>6
∴能组成三角形
解:
∵最长线段是6cm
4+3>6
∴能组成三角形
判断方法:
如果三条线段长已知,只要先找出最长的线段,如果较小的两条线段之和大于最长线段,便可构成三角形;若不满足,则不能构成三角形.
应用与探究
现在要做一个三角形的铁架子,已有两根长分别为20cm和40cm的铁条,需要再找一根铁条,把它们首尾相接焊在一起.
C
40cm
20cm
xcm
A
B
AC-AB<X
AC+AB>X
即大于20cm,小于60cm
三角形任何两边的差与第三边关系?
你能提供一个选择的范围吗?
现有长分别10cm,30cm,40cm,50cm,60cm
的五根铁条,你会选择哪一条?
变式拓展
三角形任何两边的差与第三边关系:
b
c
a
A
B
C
三角形任何两边的差小于第三边。
若三角形的两边长分别为a和b,(设a?b)则第三边c与这两条边的关系:
a-b<c<a+b
三角形的性质(三角形的三边关系)
在ΔABC中,AB=7
BC=3,并且AC为奇数,那么ΔABC的周长为____________
15,17,19
当堂检测
2、由
的三条线段
所组成的图形叫做三角形
3、若a、b、c是△ABC的三条边,化简:
|a-b-c|+|a+b-c︳
不在同一直线上
首尾顺次相接
|a-b-c|+|a+b-c︳
=b+c-a+a+b-c
=2b
1、下列说法中错误的是(
)
A.有一个角是锐角的三角形是锐角三角形
B.三角形的三个内角中至少有两个角是锐角
C.一个三角形的三个内角中至少有一个内角
60°
D.如果三角形的两个内角之和小于90°,那么这个三角形是钝角三角形
A
4、如图所示,在△ABC中,D是BA上一点,则AB+2CD>AC+BC成立吗?
说明理由.
AB+2CD>AC+BC成立,理由如下:
∵在△ADC中,AD+CD>AC,在△BCD中,BD+CD>BC,
∴(AD+BD)+2CD>AC+BC,
即AB+2CD>AC+BC.
两个关系:
多个概念:
三角形(边,内角,分类…)
三角形的三边关系:
三角形任何两边的和大于第三边.
三角形任何两边的差小于第三边.
三角形日记
∴
两边之差?第三边?两边之和
一个方法:
判断三条已知线段能否组成三角形:
满足较短的两条线段之和大于最长的一条线段,则能组成三角形;若不满足,则不能组成三角形.
若三角形的周长为13,且三边长都是正整数,那么满足条件的三角形有多少个?
巩固思考
结束寄语:
大家的学习过程就像人生中的一个三角形支架,要以学、习、悟作为支架的三边,缺一不可,有了它的支撑,我们才能更加稳固的实现自己的人生目标!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
