第1章 二次函数单元训练卷(Word版 含解析)-2021-2022学年度浙教版九年级数学上册
文档属性
| 名称 | 第1章 二次函数单元训练卷(Word版 含解析)-2021-2022学年度浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 220.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 15:50:05 | ||
图片预览




文档简介
第1章
二次函数单元训练卷-2021-2022学年度浙教版九年级数学上册
一、选择题
1.抛物线
经过点
、
,且与y轴交于点
,则当
时,y的值为(???
)
A.-5
B.-3
C.-1
D.5
2.已知抛物线
上的部分点的横坐标x与纵坐标y的对应值如表:
x
…
-1
0
1
2
3
…
y
…
3
0
-1
m
3
…
以下结论正确的是(???
)
A.?抛物线
的开口向下
B.?当
时,y随x增大而增大
C.?方程
的根为0和2
D.?当
时,x的取值范围是
3.在平面直角坐标系中,将二次函数
的图象向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为(??
)
A.???????????B.????????????C.?????????????D.?
4.如图,已如抛物线
开口向上,与
轴的一个交点为
,对称轴为直线
.下列结论错误的是(??
)
A.??????????????????????B.???????????C.?????????????????D.?
5.已知
,且
,其中
,
,则
的取值范围(??
)
A.?????????????????B.?????????????C.???????????D.?
6.如图,矩形
中,
,
,抛物线
的顶点
在矩形
内部或其边上,则
的取值范围是(
??)
A.??????????B.???????????????C.?????????D.?
7.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为(???
)人
A.?56??????????????????????????????B.?55?????????????????????????????C.?54???????????????????????????D.?53
8.小明在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数
,则小明此次成绩为(??
)
A.?8米???????????????????????B.?10米?????????????????????????C.?12米????????????????????????D.?14米
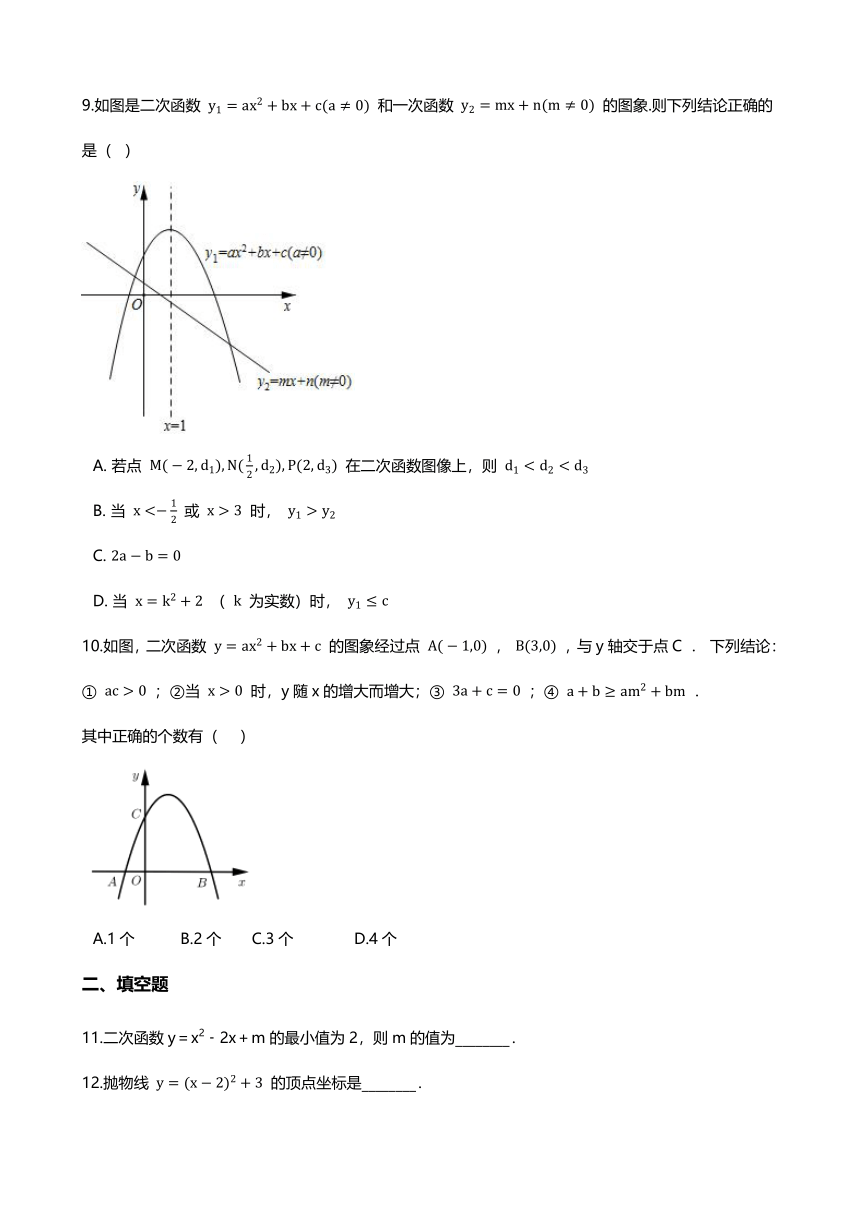
9.如图是二次函数
和一次函数
的图象.则下列结论正确的是(?
)
A.?若点
在二次函数图像上,则
B.?当
或
时,
C.?
D.?当
(
为实数)时,
10.如图,二次函数
的图象经过点
,
,与y轴交于点C
.
下列结论:
①
;②当
时,y随x的增大而增大;③
;④
.
其中正确的个数有(???
)
A.1个
B.2个
C.3个
D.4个
二、填空题
11.二次函数y=x2﹣2x+m的最小值为2,则m的值为________.
12.抛物线
的顶点坐标是________.
13.某商场经营一种小商品,已知购进时单价是20元.调查发现:当销售单价是30元时,月销售量为280件.而销售单价每上涨1元,月销售量就减少10件,当月销售利润最大时,销售单价为________元.
14.已知函数y=(a﹣1)x2﹣2ax+a﹣3的图象与两坐标轴共有两个交点,则a的值为________.
15.抛物线
经过点
,
两点,则不等式
的解集是________.
16.如图,矩形
中AB=2,AD=5,动点P从点A出发,以1
cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则
面积最小值为________.
三、解答题
17.二次函数图像的顶点坐标是(-2,3),并经过点(1,2),求这个二次函数的函数关系式.
18.如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),求当矩形ABCD的面积最大时AB的长.
19.某公司计划购进一批原料加工销售,已知该原料的进价为6.2万元/t
,
加工过程中原料的质量有20%的损耗,加工费m(万元)与原料的质量x(t)之间的关系为m=50+0.2x
,
销售价y(万元/t)与原料的质量x(t)之间的关系如图所示.
(1)求y与x之间的函数关系式;
(2)设销售收入为P(万元),求P与x之间的函数关系式;
(3)原料的质量x为多少吨时,所获销售利润最大,最大销售利润是多少万元?(销售利润=销售收入﹣总支出).
20.甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面
可视为抛物线的一部分,在某一时刻,桥拱内的水面宽
,桥拱顶点
到水面的距离是
.
(1)按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;
(2)一只宽为
的打捞船径直向桥驶来,当船驶到桥拱下方且距
点
时,桥下水位刚好在
处.有一名身高
的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);
(3)如图③,桥拱所在的函数图象是抛物线
,该抛物线在
轴下方部分与桥拱
在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移
个单位长度,平移后的函数图象在
时,
的值随
值的增大而减小,结合函数图象,求
的取值范围.
21.如图,已知抛物线y=a(x﹣3)(x+6)过点A(﹣1,5)和点B(﹣5,m)与x轴的正半轴交于点C.
(1)求a,m的值和点C的坐标;
(2)若点P是x轴上的点,连接PB,PA,当
时,求点P的坐标;
(3)在抛物线上是否存在点M,使A,B两点到直线MC的距离相等?若存在,求出满足条件的点M的横坐标;若不存在,请说明理由.
22.已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).
(1)若二次函数的图象经过点(0,4),对称轴为x=1,求此二次函数的表达式;
(2)若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;
(3)记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1
,
求实数m的最小值.
23.在平面直角坐标系中,抛物线
的顶点为A
.
(1)求顶点A的坐标(用含有字母m的代数式表示);
(2)若点
,
在抛物线上,且
,则m的取值范围是________;(直接写出结果即可)
(3)当
时,函数y的最小值等于6,求m的值.
24.在平面直角坐标系中,抛物线
交x轴于点
,
,过点B的直线
交抛物线于点C.
(1)求该抛物线的函数表达式;
(2)若点P是直线BC下方抛物线上的一个动点(P不与点B
,
C重合),求
面积的最大值;
(3)若点M在抛物线上,将线段OM绕点O旋转90°,得到线段ON
,
是否存在点M
,
使点N恰好落在直线BC上?若存在,请直接写出点M的坐标;若不存在,请说明理由.
答案
一、选择题
1.解:∵抛物线
经过点
、
,且与y轴交于点
,
∴
,
解方程组得
,
∴抛物线解析式为
,
当
时,
.
故答案为:择A.
2.解:将
代入抛物线的解析式得;
,
解得:
,
所以抛物线的解析式为:
,
A、
,抛物线开口向上,不符合题意,不符合题;
B、抛物线的对称轴为直线
,在
时,y随x增大而增大,不符合题意,不符合题意;
C、方程
的根为0和2,符合题意,符合题意;
D、当
时,x的取值范围是
或
,不符合题意,不符合题意;
故答案为:C.
3.解:∵
的顶点坐标为(0,0)
∴将二次函数
的图象向左平移2个单位长度,再向上平移1个单位长度,所得抛物线的顶点坐标为(-2,1),
∴所得抛物线对应的函数表达式为
,
故答案为:B
4.解:∵抛物线开口向上,对称轴为直线
,
∴a>0,b<0;由图象知c<0,
∴abc>0,故A不符合题意;
∵抛物线y=ax2+bx+c与x轴有两个交点,对称轴是直线x=1,与x轴的一个交点是(-1,0),
∴抛物线与x轴的另一个交点是(3,0);
∴
即
故B不符合题意;
当x=2时,
,即
,故C符合题意;
∵抛物线对称轴为直线
∴
,即
,故D不符合题意,
故答案为:C.
5.解:由
可得:
,
∵m≤3,n≥-3,
∴
,
即-2≤x≤2,
∵y=2x2-4x+1,
对称轴为直线x=
=1且a=2>0,开口向上,
∴当x=1时,y有最小值,最小值为y=2×12-4×1+1=-1,
当x=-2时,y有最大值,最大值为y=2×(-2)2-4×(-2)+1=17,
∴-1≤y≤17,
故答案为:A.
6.解:抛物线
的顶点坐标M为(m
,
-m+1),
∵
,
,
∴
,
∴-1≤m≤0,
故答案为:D
.
7.解:设旅行团人数为x人,此时的营业额为y元,则
,
由题意得:
,
由二次函数的性质可知,在
内,当
时,y取得最大值,
即若这个旅行社要获得最大营业额,此时旅行团人数为55人,
故答案为:B.
8.解:当
时,
,即
.
解得:
(舍),
.
则小明此次成绩时10米.
故答案为:B.
9.解:∵抛物线的开口向下,对称轴为直线x=1,且|-2-1|>|2-1|>
,
∴d1<d3<d2
,
故A错误;
无法求得两个函数图象的交点坐标,故B错误;
∵抛物线对称轴为直线x=1,
∴
,
∴2a+b=0,故C错误;
∵抛物线对称轴为直线x=1,
∴点(0,c)与点(2,c)关于对称轴对称,
∴当x=k2+2(k为实数)时,y1≤c,故D正确.
故答案为:D.
10.∵二次函数的图象经过点A(—1,0),B(3,
0)
∴对称轴
∴b
=-2a
,
c
=
-3a
∵二次函数的图象开口向下
∴a
<
0
∴2a+b+c
=
-3a
>0,∴ac<0故①不符合题意;
∵二次函数的图象开口向下,对称轴
,
∴当x
>1时,y随x的增大而减小;故②不符合题意;
∵c
=
-3a
∴3a+c=0,故③符合题意;
由题意可知二次函数的顶点坐标为(1,-4a)
∵当x=1时,y最大=a+b+c
,
当x=m时,y=
∴
故④符合题意;
故答案为:B
二、填空题
11.解:y=x2﹣2x+m=(x﹣1)2+m﹣1,
∵a=1>0,
∴当x=1时,y有最小值为m﹣1,
∴m﹣1=2,
∴m=3.
故答案为:3.
12.解:∵抛物线y=a(x-h)2+k的顶点坐标是(h,k),
∴抛物线
的顶点坐标是(2,3),
故答案为:(2,3).
13.解:设销售单价为x元时,销售利润最大,
单价利润为(x-20)元,
销售数量为280-(x-30)?10,
∴利润总额为y=(x-20)?[280-(x-30)?10],
化简得:y=-10x2+780x-11600,
配方得:y=-10(x-39)2+3610,
当单价为39元时,有最大利润3610元,
故答案为:39.
14.解:当a﹣1=0时,即a=1时,函数为y=﹣2x﹣2,此一次函数与坐标轴共有两个交点;
当a﹣1≠0,此函数为二次函数,
?若a﹣3=0,抛物线解析式为y=2x2﹣6x
,
抛物线经过原点且抛物线与x轴有两个交点;
?若△=0,抛物线的顶点在x轴上,即△=(﹣2a)2﹣4(a﹣1)(a﹣3)=0,
?解得:a=
,
?抛物线解析式为y=﹣
x2﹣
x﹣
=﹣
(x+3)2
,
抛物线的顶点为(﹣3,0),则抛物?
线与x轴和y轴各一个交点,则与坐标轴共有两个交点.
综上所述,a的值为1或3或
.
故答案为:1或3或
15.解:∵
∴
由
的向左平移3个单位得到,
∵抛物线
经过点
,
两点
∴
的经过点(-4,t),(2,t),
∵
∴
开口向上
∴当
或
时
即
的解集为
或
故答案:
或
16.解:由题意得:AP=t,PD=5-t,
∴
,
∵四边形PCEF是正方形,
∴
,
∵
,
∴
,
∴
,
∴当t=4时,△DEF的面积最小,最小值为
.
故答案为:
.
三、解答题
17.
解:设二次函数解析式为y=a(x+2)2+3,
把(1,2)代入得9a+3=2,解得a=
,
所以二次函数解析式为:y=
(x+2)2+3.
18.
解:设AB=xm,矩形ABCD的面积设为y(平方米),
则AB+EF+CD=3x,
∴AD=BC=
.
∴y=
=
.
由于二次项系数小于0,所以y有最大值,
∴当AB=x=
=
=150时,函数y取得最大值.
当AB=150m,矩形ABCD的面积最大
19.
(1)解:设y与x之间的函数关系式为
,
将(20,15),(30,12.5)代入,
可得:
,
解得:
,
∴y与x之间的函数关系式为
;
(2)解:设销售收入为P(万元),
∴
,
∴P与x之间的函数关系式为
;
(3)解:设销售总利润为W,
∴
,
整理,可得:
,
∵﹣
<0,
∴当
时,W有最大值为
,
∴原料的质量为24吨时,所获销售利润最大,最大销售利润是
万元.
20.
(1)解:根据题意得:A(8,0),B(4,4),
设二次函数的解析式为:y=a(x-8)x,
把(4,4)代入上式,得:4=a×(4-8)×4,解得:
,
∴二次函数的解析式为:y=
(x-8)x=
x2+2x(0≤x≤8)
(2)解:由题意得:x=0.4+1.2÷2=1,代入y=
x2+2x,得y=
×12+2×1=
>1.68,
答:他的头顶不会触碰到桥拱
(3)解:由题意得:当0≤x≤8时,新函数表达式为:y=
x2-2x,
当x<0或x>8时,新函数表达式为:y=-
x2+2x,
∴新函数表达式为:
,
∵将新函数图象向右平移
个单位长度,
∴
(m,0),
(m+8,0),
(m+4,-4),如图所示,
根据图象可知:当m+4≥9且m≤8时,即:5≤m≤8时,平移后的函数图象在
时,
的值随
值的增大而减小.
21
(1)解:把
代入函数解析式得:
?
?
把
代入
?
令
?
?
结合题意可得:
(2)解:如图,设
而
?
则
?
?
?
?
?
(3)解:存在,理由如下:
如图,连接
过
作
交抛物线于
则
到直线
的距离相等,
设直线
为
?得:
?直线
为
由
设
为
,而
?则直线
为
?
解得:
或
?
如图,当
过
的中点
时,则
到
的距离相等,
?则
同理可得:
的解析式为:
?
解得:
或
?
综上:
或
22.
(1)解:∵二次函数的图象经过点(0,4),
∴c=4;
∵对称轴为直线:x=﹣
=1,
∴b=﹣2,
∴此二次函数的表达式为:y1=x2﹣2x+4
(2)解:当b2﹣c=0时,b2=c,此时函数的表达式为:y1=x2+bx+b2
,
根据题意可知,需要分三种情况:
①当b<﹣
,即b<0时,二次函数的最小值在x=b处取到;
∴b2+b2+b2=21,解得b=
,b=﹣
舍去;
②b﹣3>﹣
,即b>2时,二次函数的最小值在x=b﹣3处取到;
∴(b﹣3)2+b(b﹣3)+b2=21,解得b=4,b=﹣1(舍去);
③b﹣3≤﹣
≤b,即0≤b≤2时,二次函数的最小值在x=﹣
处取到;
∴(﹣
)2+b?(﹣
)+b2=21,解得b=±2
(舍去).
综上,b的取值为
或4.
(3)解:由(1)知,二次函数的表达式为:y1=x2﹣2x+4,
对称轴为直线:x=1,
∵1>0,
∴当0≤x≤1时,y随x的增大而减小,且最大值为4;
∵二次函数y2=2x2+x+m的对称轴为直线:x=﹣
,且2>0,
∴当0≤x≤1时,y随x的增大而增大,且最小值为m,
∵当0≤x≤1时,总有y2≥y1
,
∴m≥4,即m的最小值为4.
23.
(1)解:由题意可知:
抛物线
,
∴顶点A的坐标为
(2)
(3)解:二次函数的开口向上,故自变量离对称轴越远,其对应的函数值越大,二次函数的对称轴为
,
分类讨论:
①当
,即
时,
时二次函数取得最小值为
,
又已知二次函数最小值为6,
∴
,解得
或
,
又
,故
符合题意;
②当
,即
时,
时二次函数取得最小值为
,
又已知二次函数最小值为6,
∴
,解得
或
,
又
,故
或
都不符合题意;
③当
,即
时,
时二次函数取得最小值为
,
又已知二次函数最小值为6,
∴
,解得
或
,
又
,故
符合题意;
综上所述,
或
解:(2)将
代入
中,
?得到
,
将
代入
中,
得到
,
由已知条件知:
,
∴
,
整理得到:
,
解得:
,
故m的取值范围是:
;
24.
(1)解:将点
,
代入
中,得:
解得
∴该抛物线表达式为
(2)解:过点P作
轴,交x轴于点D,交BC于点E,作
于点F,连接PB,PC,如图.
设点
,则点
.
∵点P、E均位于直线
的下方
∴P、E两点的纵坐标均为负
∴
,
∴
∵点C的坐标为方程组
的一个解
∴解这个方程组,得
,
∵点B坐标为
∴点C的横坐标为
∴
∴
.(其中
)
∵
∴这个二次函数有最大值,且当
时,
的最大值为
(3)解:存在
设M(p,q),其中
,且p≠0,
则直线OM的解析式为:
由于ON⊥OM,则直线ON的解析式为:
解方程组
,得
,
即点N的坐标为
∴
∵
,且OM=ON
∴
∴
即
或
把
代入两式中并整理,得:
或
解方程得:
?,
,
,
(舍去)
当
时,
;当
时,
;当
时,
故点M的坐标分别为:
或
或
当p=0时,则q=-3,即M(0,-3),而
,且OM⊥OB
即此时点M也满足题意
综上所述,满足题意的点M的坐标为
或
或
或
?
二次函数单元训练卷-2021-2022学年度浙教版九年级数学上册
一、选择题
1.抛物线
经过点
、
,且与y轴交于点
,则当
时,y的值为(???
)
A.-5
B.-3
C.-1
D.5
2.已知抛物线
上的部分点的横坐标x与纵坐标y的对应值如表:
x
…
-1
0
1
2
3
…
y
…
3
0
-1
m
3
…
以下结论正确的是(???
)
A.?抛物线
的开口向下
B.?当
时,y随x增大而增大
C.?方程
的根为0和2
D.?当
时,x的取值范围是
3.在平面直角坐标系中,将二次函数
的图象向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为(??
)
A.???????????B.????????????C.?????????????D.?
4.如图,已如抛物线
开口向上,与
轴的一个交点为
,对称轴为直线
.下列结论错误的是(??
)
A.??????????????????????B.???????????C.?????????????????D.?
5.已知
,且
,其中
,
,则
的取值范围(??
)
A.?????????????????B.?????????????C.???????????D.?
6.如图,矩形
中,
,
,抛物线
的顶点
在矩形
内部或其边上,则
的取值范围是(
??)
A.??????????B.???????????????C.?????????D.?
7.某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,每人的单价就降低10元,若这个旅行社要获得最大营业额,此时旅行团人数为(???
)人
A.?56??????????????????????????????B.?55?????????????????????????????C.?54???????????????????????????D.?53
8.小明在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数
,则小明此次成绩为(??
)
A.?8米???????????????????????B.?10米?????????????????????????C.?12米????????????????????????D.?14米
9.如图是二次函数
和一次函数
的图象.则下列结论正确的是(?
)
A.?若点
在二次函数图像上,则
B.?当
或
时,
C.?
D.?当
(
为实数)时,
10.如图,二次函数
的图象经过点
,
,与y轴交于点C
.
下列结论:
①
;②当
时,y随x的增大而增大;③
;④
.
其中正确的个数有(???
)
A.1个
B.2个
C.3个
D.4个
二、填空题
11.二次函数y=x2﹣2x+m的最小值为2,则m的值为________.
12.抛物线
的顶点坐标是________.
13.某商场经营一种小商品,已知购进时单价是20元.调查发现:当销售单价是30元时,月销售量为280件.而销售单价每上涨1元,月销售量就减少10件,当月销售利润最大时,销售单价为________元.
14.已知函数y=(a﹣1)x2﹣2ax+a﹣3的图象与两坐标轴共有两个交点,则a的值为________.
15.抛物线
经过点
,
两点,则不等式
的解集是________.
16.如图,矩形
中AB=2,AD=5,动点P从点A出发,以1
cm/s的速度沿AD向终点D移动,设移动时间为t(s).连接PC,以PC为一边作正方形PCEF,连接DE、DF,则
面积最小值为________.
三、解答题
17.二次函数图像的顶点坐标是(-2,3),并经过点(1,2),求这个二次函数的函数关系式.
18.如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),求当矩形ABCD的面积最大时AB的长.
19.某公司计划购进一批原料加工销售,已知该原料的进价为6.2万元/t
,
加工过程中原料的质量有20%的损耗,加工费m(万元)与原料的质量x(t)之间的关系为m=50+0.2x
,
销售价y(万元/t)与原料的质量x(t)之间的关系如图所示.
(1)求y与x之间的函数关系式;
(2)设销售收入为P(万元),求P与x之间的函数关系式;
(3)原料的质量x为多少吨时,所获销售利润最大,最大销售利润是多少万元?(销售利润=销售收入﹣总支出).
20.甲秀楼是贵阳市一张靓丽的名片.如图①,甲秀楼的桥拱截面
可视为抛物线的一部分,在某一时刻,桥拱内的水面宽
,桥拱顶点
到水面的距离是
.
(1)按如图②所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式;
(2)一只宽为
的打捞船径直向桥驶来,当船驶到桥拱下方且距
点
时,桥下水位刚好在
处.有一名身高
的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱,请说明理由(假设船底与水面齐平);
(3)如图③,桥拱所在的函数图象是抛物线
,该抛物线在
轴下方部分与桥拱
在平静水面中的倒影组成一个新函数图象.将新函数图象向右平移
个单位长度,平移后的函数图象在
时,
的值随
值的增大而减小,结合函数图象,求
的取值范围.
21.如图,已知抛物线y=a(x﹣3)(x+6)过点A(﹣1,5)和点B(﹣5,m)与x轴的正半轴交于点C.
(1)求a,m的值和点C的坐标;
(2)若点P是x轴上的点,连接PB,PA,当
时,求点P的坐标;
(3)在抛物线上是否存在点M,使A,B两点到直线MC的距离相等?若存在,求出满足条件的点M的横坐标;若不存在,请说明理由.
22.已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).
(1)若二次函数的图象经过点(0,4),对称轴为x=1,求此二次函数的表达式;
(2)若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;
(3)记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1
,
求实数m的最小值.
23.在平面直角坐标系中,抛物线
的顶点为A
.
(1)求顶点A的坐标(用含有字母m的代数式表示);
(2)若点
,
在抛物线上,且
,则m的取值范围是________;(直接写出结果即可)
(3)当
时,函数y的最小值等于6,求m的值.
24.在平面直角坐标系中,抛物线
交x轴于点
,
,过点B的直线
交抛物线于点C.
(1)求该抛物线的函数表达式;
(2)若点P是直线BC下方抛物线上的一个动点(P不与点B
,
C重合),求
面积的最大值;
(3)若点M在抛物线上,将线段OM绕点O旋转90°,得到线段ON
,
是否存在点M
,
使点N恰好落在直线BC上?若存在,请直接写出点M的坐标;若不存在,请说明理由.
答案
一、选择题
1.解:∵抛物线
经过点
、
,且与y轴交于点
,
∴
,
解方程组得
,
∴抛物线解析式为
,
当
时,
.
故答案为:择A.
2.解:将
代入抛物线的解析式得;
,
解得:
,
所以抛物线的解析式为:
,
A、
,抛物线开口向上,不符合题意,不符合题;
B、抛物线的对称轴为直线
,在
时,y随x增大而增大,不符合题意,不符合题意;
C、方程
的根为0和2,符合题意,符合题意;
D、当
时,x的取值范围是
或
,不符合题意,不符合题意;
故答案为:C.
3.解:∵
的顶点坐标为(0,0)
∴将二次函数
的图象向左平移2个单位长度,再向上平移1个单位长度,所得抛物线的顶点坐标为(-2,1),
∴所得抛物线对应的函数表达式为
,
故答案为:B
4.解:∵抛物线开口向上,对称轴为直线
,
∴a>0,b<0;由图象知c<0,
∴abc>0,故A不符合题意;
∵抛物线y=ax2+bx+c与x轴有两个交点,对称轴是直线x=1,与x轴的一个交点是(-1,0),
∴抛物线与x轴的另一个交点是(3,0);
∴
即
故B不符合题意;
当x=2时,
,即
,故C符合题意;
∵抛物线对称轴为直线
∴
,即
,故D不符合题意,
故答案为:C.
5.解:由
可得:
,
∵m≤3,n≥-3,
∴
,
即-2≤x≤2,
∵y=2x2-4x+1,
对称轴为直线x=
=1且a=2>0,开口向上,
∴当x=1时,y有最小值,最小值为y=2×12-4×1+1=-1,
当x=-2时,y有最大值,最大值为y=2×(-2)2-4×(-2)+1=17,
∴-1≤y≤17,
故答案为:A.
6.解:抛物线
的顶点坐标M为(m
,
-m+1),
∵
,
,
∴
,
∴-1≤m≤0,
故答案为:D
.
7.解:设旅行团人数为x人,此时的营业额为y元,则
,
由题意得:
,
由二次函数的性质可知,在
内,当
时,y取得最大值,
即若这个旅行社要获得最大营业额,此时旅行团人数为55人,
故答案为:B.
8.解:当
时,
,即
.
解得:
(舍),
.
则小明此次成绩时10米.
故答案为:B.
9.解:∵抛物线的开口向下,对称轴为直线x=1,且|-2-1|>|2-1|>
,
∴d1<d3<d2
,
故A错误;
无法求得两个函数图象的交点坐标,故B错误;
∵抛物线对称轴为直线x=1,
∴
,
∴2a+b=0,故C错误;
∵抛物线对称轴为直线x=1,
∴点(0,c)与点(2,c)关于对称轴对称,
∴当x=k2+2(k为实数)时,y1≤c,故D正确.
故答案为:D.
10.∵二次函数的图象经过点A(—1,0),B(3,
0)
∴对称轴
∴b
=-2a
,
c
=
-3a
∵二次函数的图象开口向下
∴a
<
0
∴2a+b+c
=
-3a
>0,∴ac<0故①不符合题意;
∵二次函数的图象开口向下,对称轴
,
∴当x
>1时,y随x的增大而减小;故②不符合题意;
∵c
=
-3a
∴3a+c=0,故③符合题意;
由题意可知二次函数的顶点坐标为(1,-4a)
∵当x=1时,y最大=a+b+c
,
当x=m时,y=
∴
故④符合题意;
故答案为:B
二、填空题
11.解:y=x2﹣2x+m=(x﹣1)2+m﹣1,
∵a=1>0,
∴当x=1时,y有最小值为m﹣1,
∴m﹣1=2,
∴m=3.
故答案为:3.
12.解:∵抛物线y=a(x-h)2+k的顶点坐标是(h,k),
∴抛物线
的顶点坐标是(2,3),
故答案为:(2,3).
13.解:设销售单价为x元时,销售利润最大,
单价利润为(x-20)元,
销售数量为280-(x-30)?10,
∴利润总额为y=(x-20)?[280-(x-30)?10],
化简得:y=-10x2+780x-11600,
配方得:y=-10(x-39)2+3610,
当单价为39元时,有最大利润3610元,
故答案为:39.
14.解:当a﹣1=0时,即a=1时,函数为y=﹣2x﹣2,此一次函数与坐标轴共有两个交点;
当a﹣1≠0,此函数为二次函数,
?若a﹣3=0,抛物线解析式为y=2x2﹣6x
,
抛物线经过原点且抛物线与x轴有两个交点;
?若△=0,抛物线的顶点在x轴上,即△=(﹣2a)2﹣4(a﹣1)(a﹣3)=0,
?解得:a=
,
?抛物线解析式为y=﹣
x2﹣
x﹣
=﹣
(x+3)2
,
抛物线的顶点为(﹣3,0),则抛物?
线与x轴和y轴各一个交点,则与坐标轴共有两个交点.
综上所述,a的值为1或3或
.
故答案为:1或3或
15.解:∵
∴
由
的向左平移3个单位得到,
∵抛物线
经过点
,
两点
∴
的经过点(-4,t),(2,t),
∵
∴
开口向上
∴当
或
时
即
的解集为
或
故答案:
或
16.解:由题意得:AP=t,PD=5-t,
∴
,
∵四边形PCEF是正方形,
∴
,
∵
,
∴
,
∴
,
∴当t=4时,△DEF的面积最小,最小值为
.
故答案为:
.
三、解答题
17.
解:设二次函数解析式为y=a(x+2)2+3,
把(1,2)代入得9a+3=2,解得a=
,
所以二次函数解析式为:y=
(x+2)2+3.
18.
解:设AB=xm,矩形ABCD的面积设为y(平方米),
则AB+EF+CD=3x,
∴AD=BC=
.
∴y=
=
.
由于二次项系数小于0,所以y有最大值,
∴当AB=x=
=
=150时,函数y取得最大值.
当AB=150m,矩形ABCD的面积最大
19.
(1)解:设y与x之间的函数关系式为
,
将(20,15),(30,12.5)代入,
可得:
,
解得:
,
∴y与x之间的函数关系式为
;
(2)解:设销售收入为P(万元),
∴
,
∴P与x之间的函数关系式为
;
(3)解:设销售总利润为W,
∴
,
整理,可得:
,
∵﹣
<0,
∴当
时,W有最大值为
,
∴原料的质量为24吨时,所获销售利润最大,最大销售利润是
万元.
20.
(1)解:根据题意得:A(8,0),B(4,4),
设二次函数的解析式为:y=a(x-8)x,
把(4,4)代入上式,得:4=a×(4-8)×4,解得:
,
∴二次函数的解析式为:y=
(x-8)x=
x2+2x(0≤x≤8)
(2)解:由题意得:x=0.4+1.2÷2=1,代入y=
x2+2x,得y=
×12+2×1=
>1.68,
答:他的头顶不会触碰到桥拱
(3)解:由题意得:当0≤x≤8时,新函数表达式为:y=
x2-2x,
当x<0或x>8时,新函数表达式为:y=-
x2+2x,
∴新函数表达式为:
,
∵将新函数图象向右平移
个单位长度,
∴
(m,0),
(m+8,0),
(m+4,-4),如图所示,
根据图象可知:当m+4≥9且m≤8时,即:5≤m≤8时,平移后的函数图象在
时,
的值随
值的增大而减小.
21
(1)解:把
代入函数解析式得:
?
?
把
代入
?
令
?
?
结合题意可得:
(2)解:如图,设
而
?
则
?
?
?
?
?
(3)解:存在,理由如下:
如图,连接
过
作
交抛物线于
则
到直线
的距离相等,
设直线
为
?得:
?直线
为
由
设
为
,而
?则直线
为
?
解得:
或
?
如图,当
过
的中点
时,则
到
的距离相等,
?则
同理可得:
的解析式为:
?
解得:
或
?
综上:
或
22.
(1)解:∵二次函数的图象经过点(0,4),
∴c=4;
∵对称轴为直线:x=﹣
=1,
∴b=﹣2,
∴此二次函数的表达式为:y1=x2﹣2x+4
(2)解:当b2﹣c=0时,b2=c,此时函数的表达式为:y1=x2+bx+b2
,
根据题意可知,需要分三种情况:
①当b<﹣
,即b<0时,二次函数的最小值在x=b处取到;
∴b2+b2+b2=21,解得b=
,b=﹣
舍去;
②b﹣3>﹣
,即b>2时,二次函数的最小值在x=b﹣3处取到;
∴(b﹣3)2+b(b﹣3)+b2=21,解得b=4,b=﹣1(舍去);
③b﹣3≤﹣
≤b,即0≤b≤2时,二次函数的最小值在x=﹣
处取到;
∴(﹣
)2+b?(﹣
)+b2=21,解得b=±2
(舍去).
综上,b的取值为
或4.
(3)解:由(1)知,二次函数的表达式为:y1=x2﹣2x+4,
对称轴为直线:x=1,
∵1>0,
∴当0≤x≤1时,y随x的增大而减小,且最大值为4;
∵二次函数y2=2x2+x+m的对称轴为直线:x=﹣
,且2>0,
∴当0≤x≤1时,y随x的增大而增大,且最小值为m,
∵当0≤x≤1时,总有y2≥y1
,
∴m≥4,即m的最小值为4.
23.
(1)解:由题意可知:
抛物线
,
∴顶点A的坐标为
(2)
(3)解:二次函数的开口向上,故自变量离对称轴越远,其对应的函数值越大,二次函数的对称轴为
,
分类讨论:
①当
,即
时,
时二次函数取得最小值为
,
又已知二次函数最小值为6,
∴
,解得
或
,
又
,故
符合题意;
②当
,即
时,
时二次函数取得最小值为
,
又已知二次函数最小值为6,
∴
,解得
或
,
又
,故
或
都不符合题意;
③当
,即
时,
时二次函数取得最小值为
,
又已知二次函数最小值为6,
∴
,解得
或
,
又
,故
符合题意;
综上所述,
或
解:(2)将
代入
中,
?得到
,
将
代入
中,
得到
,
由已知条件知:
,
∴
,
整理得到:
,
解得:
,
故m的取值范围是:
;
24.
(1)解:将点
,
代入
中,得:
解得
∴该抛物线表达式为
(2)解:过点P作
轴,交x轴于点D,交BC于点E,作
于点F,连接PB,PC,如图.
设点
,则点
.
∵点P、E均位于直线
的下方
∴P、E两点的纵坐标均为负
∴
,
∴
∵点C的坐标为方程组
的一个解
∴解这个方程组,得
,
∵点B坐标为
∴点C的横坐标为
∴
∴
.(其中
)
∵
∴这个二次函数有最大值,且当
时,
的最大值为
(3)解:存在
设M(p,q),其中
,且p≠0,
则直线OM的解析式为:
由于ON⊥OM,则直线ON的解析式为:
解方程组
,得
,
即点N的坐标为
∴
∵
,且OM=ON
∴
∴
即
或
把
代入两式中并整理,得:
或
解方程得:
?,
,
,
(舍去)
当
时,
;当
时,
;当
时,
故点M的坐标分别为:
或
或
当p=0时,则q=-3,即M(0,-3),而
,且OM⊥OB
即此时点M也满足题意
综上所述,满足题意的点M的坐标为
或
或
或
?
同课章节目录
