第1章 三角形的初步知识单元训练卷(Word版含解析)-2021-2022学年度浙教版八年级数学上册
文档属性
| 名称 | 第1章 三角形的初步知识单元训练卷(Word版含解析)-2021-2022学年度浙教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 186.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 00:00:00 | ||
图片预览




文档简介
第1章
三角形的初步知识单元训练卷-2021-2022学年度浙教版八年级数学上册
一、选择题
1.下列各组分别是三根木棒的长度,其中能构成三角形的是(??
)
A.4cm,7cm,3cm
B.2cm,2.5cm,5cm
C.4.5cm,10cm,5cm
D.7cm,8cm,9cm
2.下列语句中是命题的是(??
)
A.延长线段
到
B.锐角都相等吗
C.过点
作直线
D.垂线段最短
3.如图,已知直线m∥n,∠1=40°,则∠3的度数为(??
)
A.80°
B.70°
C.60°
D.50°
4.如图,△ABC≌△DEF,∠A=63°,∠B=70°,则∠F的度数为(??
)
A.47°
B.43°
C.45°
D.40°
5.如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于
AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是(??
)
A.?AN=NC???????????????????B.?AN=BN???????????????????C.?MN=
BC???????????????D.?BN平分∠ABC
6.甲、乙两位同学分别用尺规作图法作∠AOB的平分线OC,则他们两人的作图方法(?
)
A.甲、乙两人均正确
B.甲正确,乙不正确
C.甲不正确,乙正确
D.甲、乙两人均不正确
7.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在
的两边
、
上分别在取
,移动角尺,使角尺两边相同的刻度分别与点
、
重合,这时过角尺顶点
的射线
就是
的平分线.这里构造全等三角形的依据是(??
)
A.??????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
8.如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是(??
)
A.10.5
B.12
C.15
D.18
9.直线
、
、
、
如图所示,
,
,则下列结论错误的是(??
)
A.?????????????B.?????????C.??????D.?
10.如图,在△ABC中,∠A=78°,∠EBD=∠EDB,DF平分∠EDC,则∠BDF的度数为(?
)
A.35°
B.39°
C.40°
D.45°
二、填空题
11.有一座小山,现要在小山的A,B两端开一条隧道,如图,施工队要知道A,B之间的距离,于是先在平地上取一可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量,DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为________m.
12.将一副三角板按如图摆放,已知直线
,则
的度数为________.
?
13.将一副三角板如图所示摆放,若
,那么∠1的度数为________.
14.把命题“两直线平行,同旁内角互补”改写成“如果……,那么……”的形式为________.
15.如图,
平分
,
在
上,
于
,
于
.若
,则
________
.
16.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC
,
AB于点M
,
N
,
再分别以点M
,
N为圆心,大于
MN的长为半径画弧,两弧交于点P
,
作射线AP交边BC于点D
,
若CD=4,AB=15,则△ABD的面积是________.
17.如图,
,
,
,且
,则
________
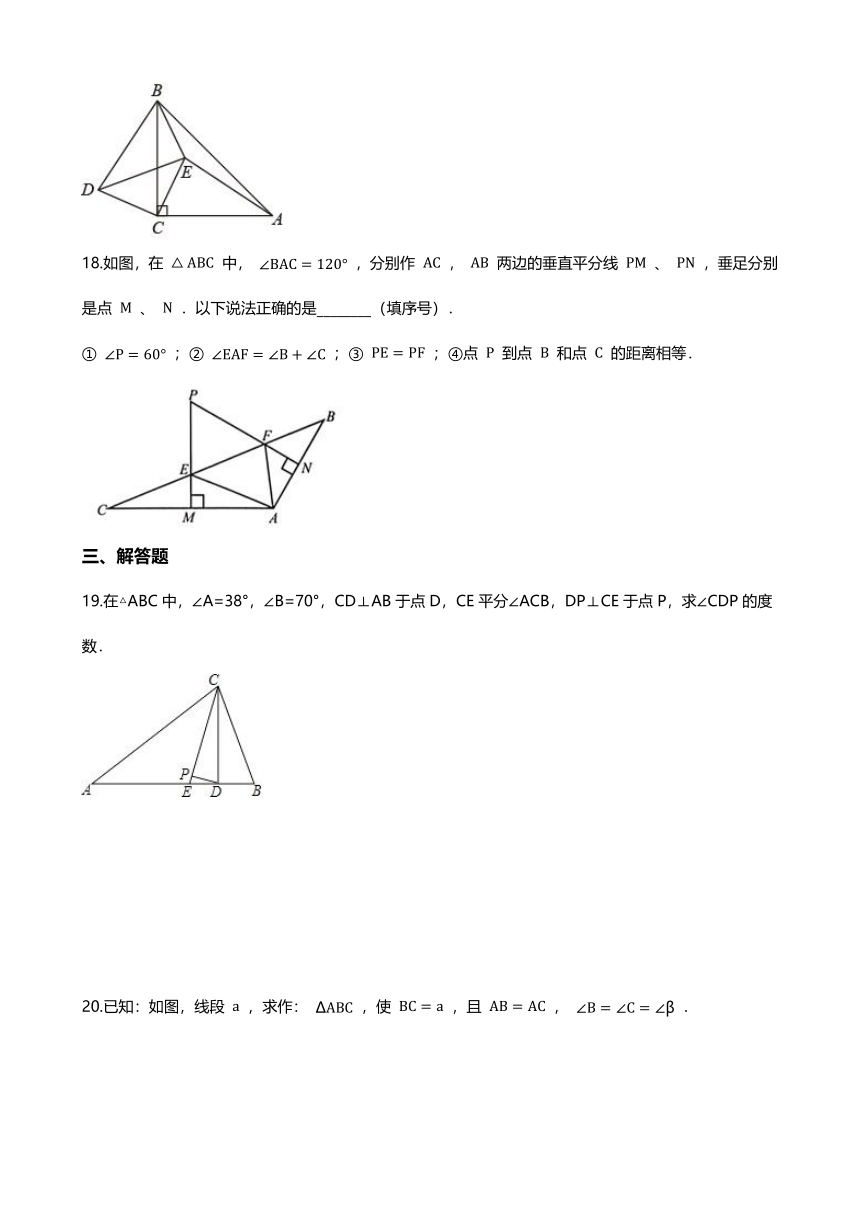
18.如图,在
中,
,分别作
,
两边的垂直平分线
、
,垂足分别是点
、
.以下说法正确的是________(填序号).
①
;②
;③
;④点
到点
和点
的距离相等.
解答题
19.在△ABC中,∠A=38°,∠B=70°,CD⊥AB于点D,CE平分∠ACB,DP⊥CE于点P,求∠CDP的度数.
20.已知:如图,线段
,求作:
,使
,且
,
.
21..如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
22.如图,已知∠1+∠2=180o
,
∠3=∠B,试说明∠DEC+∠C=180o.请完成下列填空:
解:∵∠1+∠2=180o(已知)
又∵∠1+∠4=180o(平角定义)
∴∠2=∠4(?????
)
∴_▲_∥_▲_(?????
)
∴∠3
=
∠ADE(?????
)
又∵∠3=∠B(已知)
∴∠ADE=∠B(等量代换)
∴BC∥_▲_(?????
)
∴∠DEC+∠C=180o(?????
)
23.如图,
是
的边
上一点,
,
交
于
点,
.
(1)求证:
≌
;
(2)若
,
,求
的长.
24.已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=
90°,AB=AC,AD=AE,点C、D、E在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)线段BD与线段CE的关系为________(数量关系和位置关系),请说明理由.
25.综合与探究:问题情景:如图1所示,已知,在△ABC中,AC=BA,∠ACB=90°,AD是△ABC的中线,过点C作CE⊥AD,垂足为M,且交AB于点E.
(1)(探究一)小虎通过度量发现∠BCE=∠CAD,请你帮他说明理由;
(2)(探究二)小明在图中添加了一条线段CN,且CN平分∠ACB交AD于点N,如图2所示,即可得CN=BE,符合题意吗?请说明理由;
(3)(探究三)小刚在(2)的基础上,连接DE,如图3所示,又发现了一组全等三角形,你能发现吗?请找出来,并说明理由.
答案
一、选择题
1.解:A、∵4cm+3cm=7cm,∴不能构成三角形,故本选项错误;
B、∵2cm+2.5cm=4.5cm<5cm,∴不能构成三角形,故本选项错误;
C、∵4.5cm+5cm=9.5cm<10cm,∴不能构成三角形,故本选项错误;
D、∵8cm-7cm<9cm<7cm+8cm,∴能构成三角形,故本选项正确.
故答案为:D.
2.解:A.命题是表示肯定与否定的语句,
延长线段
到
是作法,没有肯定和否定
故答案为:A不是命题,
B.锐角都相等吗是疑问句,不是肯定句或否定句,
故答案为:B不是命题;
C.
过点
作直线
,是作图语言,不是肯定或否定句,
故答案为:C不是命题;
D.垂线段最短是肯定句,是命题.
故答案为:D.
3.解:如图,
∵直线m∥n,∠1=40°,
∴∠4=∠1=40°,
∵∠3=∠2+∠2,∠2=30°,
∴∠3=30°+40°=70°,
故答案为:B.
4.∵△ABC≌△DEF,∠A=63°,∠B=70°
∴∠A=∠D=63°,∠B=∠DEF=70°
根据三角形的内角和可得∠F=180°-63°-70°=47°
故答案为:A.
5.解:由作法得DE垂直平分AB,
∴NA=NB.
故答案为:B.
6.解:由图知,甲、乙两位同学分别用尺规作图法作∠AOB的平分线OC,则他们两人的作图方法甲错误,乙正确,
故答案为:C.
7.解:由题意可知
在
中
∴
(SSS)
∴
∴
就是
的平分线
故答案为:D
8.解:∵DE是△ABC的边BC的垂直平分线,
∴BD=DC
∴AB=AD+BD=AD+DC=9
∵AC=6
∴△ACD的周长=AD+DC+AC=9+6=15
故答案为:C
9.解:∵
,∴
,故A选项正确;
∵
,
∴
,
∵
,
∴
,故B选项正确;
,故C选项正确;
∵
,
∴EF=BE,故D选项错误,
故答案为:D.
10.解:设
,
∵∠EBD=∠EDB,
∴
,
∵DF平分∠EDC,
∴
,
∴
,
∵
,∠A=78°,
∴
,
解得
,
故答案为:B.
二、填空题
11.解:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),AB=DE=800
m.答:A
,B之间的距离为800m.故答案是800.
12.解:如图,
∵m∥n,即DE∥AB,
∴∠EDA+∠DAB=180°,
即∠1+∠CDA+∠DAC+∠CAB=180°,
∵∠CDA=90°,∠DAC=45°,∠CAB=30°,
∴∠1=180°
90°
45°
30°=15°.
故答案为:15°.
13.解:过点F作FG∥DE
∵BC∥DE
,
FG∥DE
∴BC∥FG∥DE
∴∠ABC=∠GFB=30°,∠DEF=∠GFE=45°
∴∠1=∠GFB+∠GFE=75°
故答案为:75°.
14.解:根据“如果”后面接的部分是题设,“那么”后面解的部分是结论可得:两直线平行,
同旁内角互补”改写成“如果……,那么……”的形式为:如果两条平行线被第三条直线所截,那么截得的同旁内角互补.
故答案是:如果两条平行线被第三条直线所截,那么截得的同旁内角互补.
15.解:∵OC平分∠AOB,点P在OC上,且PD⊥OA于D,PE⊥OB于E,PD=3cm,
∴PE=PD=3.
故答案为:3.
16.解:作
于E
,
如图,
由作法得AP平分∠BAC
,
∴
,
∴△ABD的面积=
.
故答案为:30.
17.解:
,
,
即
,
在
和
中,
,
∴△ACE≌△BCD(SAS)
,
,
在
中,
,
在
中,
.
故答案为:140°
18.解:∵PM垂直平分AC,PN垂直平分AB,
∴∠PMA=∠PNA=90°,∠BAC=120°
∴∠P=360°-90°-90°-120°=60°,①说法符合题意;
∵∠BAC=120°,
∴∠B+∠C=180°-120°=60°,
∵PM垂直平分AC,PN垂直平分AB,
∴EC=EA,FB=FA,
∴∠EAC=∠C,∠FAB=∠B,
∴∠EAF=∠BAC-∠EAC-∠FAB=∠BAC-(∠B+∠C)=120°-60°=60°,
∴
∠EAF=∠B+∠C,②说法符合题意;
△ABC不一定是等腰三角形,
∴PE与PF的大小无法确定,③说法不符合题意;
连接PC、PA、PB
,
?
∵PM垂直平分AC
,
PN垂直平分AB
,
∴PC=PA
,
PB=PA
,
∴PB=PC
,
即点P到点B和点C的距离相等,④说法符合题意,
故答案为:①②④.
三、解答题
19.
解:∵∠A=38°,∠B=70°,
∴∠BAC=180°﹣∠A﹣∠B=180°﹣38°﹣70°=72°,
∵CE平分∠ACB,
∴∠ACE=
∠ACB=
×72°=36°,
∵CD⊥AB,
∴∠ACD=90°﹣∠A=90°﹣38°=52°,
∴∠DCE=∠ACD﹣∠ACE=52°﹣36°=16°,
∵DP⊥CE,
∴∠CDP=90°﹣∠DCE=90°﹣16°=74°.
20.
解:如图,△ABC即为所求.
21.
证明:由图可知:
,
,
∵
,
∴
,
在
和
中:
,
∴
22.
解:如图,
∵∠1+∠2=180°(已知),
又∵∠1+∠4=180°(平角定义),
∴∠2=∠4(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行
),
∴∠3=∠ADE(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴
∠ADE=∠B(等量代换),
∴BC∥DE(同位角相等,两直线平行),
∴∠DEC+∠C=180°(两直线平行,同旁内角互补),
23.
(1)证明:
,
,
在
和
中,
(2)解:由(1)得
∴
24.
(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,∴∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
(2)解:BD=CE,BD⊥CE
,理由如下:
由(1)知,△BAD≌△CAE,BD=CE,∠BDA=∠E,
∴∠E+∠ADE=
90°,
∴∠BDA+∠ADE=∠BDE=90°,即BD⊥CE.
25.
(1)证明:如图1中,
,
,
,
,
,
.
(2)结论:
符合题意.
理由:如图2中,
平分
,
,
,
,
,
,
在
和
中,
,
,
.
(3)结论:
.
理由:
是
的中点,
,
在
和
中,
,
.
三角形的初步知识单元训练卷-2021-2022学年度浙教版八年级数学上册
一、选择题
1.下列各组分别是三根木棒的长度,其中能构成三角形的是(??
)
A.4cm,7cm,3cm
B.2cm,2.5cm,5cm
C.4.5cm,10cm,5cm
D.7cm,8cm,9cm
2.下列语句中是命题的是(??
)
A.延长线段
到
B.锐角都相等吗
C.过点
作直线
D.垂线段最短
3.如图,已知直线m∥n,∠1=40°,则∠3的度数为(??
)
A.80°
B.70°
C.60°
D.50°
4.如图,△ABC≌△DEF,∠A=63°,∠B=70°,则∠F的度数为(??
)
A.47°
B.43°
C.45°
D.40°
5.如图,在△ABC中,AC>BC,分别以点A,B为圆心,以大于
AB的长为半径画弧,两弧交于D,E,经过D,E作直线分别交AB,AC于点M,N,连接BN,下列结论正确的是(??
)
A.?AN=NC???????????????????B.?AN=BN???????????????????C.?MN=
BC???????????????D.?BN平分∠ABC
6.甲、乙两位同学分别用尺规作图法作∠AOB的平分线OC,则他们两人的作图方法(?
)
A.甲、乙两人均正确
B.甲正确,乙不正确
C.甲不正确,乙正确
D.甲、乙两人均不正确
7.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在
的两边
、
上分别在取
,移动角尺,使角尺两边相同的刻度分别与点
、
重合,这时过角尺顶点
的射线
就是
的平分线.这里构造全等三角形的依据是(??
)
A.??????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
8.如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是(??
)
A.10.5
B.12
C.15
D.18
9.直线
、
、
、
如图所示,
,
,则下列结论错误的是(??
)
A.?????????????B.?????????C.??????D.?
10.如图,在△ABC中,∠A=78°,∠EBD=∠EDB,DF平分∠EDC,则∠BDF的度数为(?
)
A.35°
B.39°
C.40°
D.45°
二、填空题
11.有一座小山,现要在小山的A,B两端开一条隧道,如图,施工队要知道A,B之间的距离,于是先在平地上取一可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE.经测量,DE,EC,DC的长度分别为800m,500m,400m,则A,B之间的距离为________m.
12.将一副三角板按如图摆放,已知直线
,则
的度数为________.
?
13.将一副三角板如图所示摆放,若
,那么∠1的度数为________.
14.把命题“两直线平行,同旁内角互补”改写成“如果……,那么……”的形式为________.
15.如图,
平分
,
在
上,
于
,
于
.若
,则
________
.
16.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC
,
AB于点M
,
N
,
再分别以点M
,
N为圆心,大于
MN的长为半径画弧,两弧交于点P
,
作射线AP交边BC于点D
,
若CD=4,AB=15,则△ABD的面积是________.
17.如图,
,
,
,且
,则
________
18.如图,在
中,
,分别作
,
两边的垂直平分线
、
,垂足分别是点
、
.以下说法正确的是________(填序号).
①
;②
;③
;④点
到点
和点
的距离相等.
解答题
19.在△ABC中,∠A=38°,∠B=70°,CD⊥AB于点D,CE平分∠ACB,DP⊥CE于点P,求∠CDP的度数.
20.已知:如图,线段
,求作:
,使
,且
,
.
21..如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
22.如图,已知∠1+∠2=180o
,
∠3=∠B,试说明∠DEC+∠C=180o.请完成下列填空:
解:∵∠1+∠2=180o(已知)
又∵∠1+∠4=180o(平角定义)
∴∠2=∠4(?????
)
∴_▲_∥_▲_(?????
)
∴∠3
=
∠ADE(?????
)
又∵∠3=∠B(已知)
∴∠ADE=∠B(等量代换)
∴BC∥_▲_(?????
)
∴∠DEC+∠C=180o(?????
)
23.如图,
是
的边
上一点,
,
交
于
点,
.
(1)求证:
≌
;
(2)若
,
,求
的长.
24.已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=
90°,AB=AC,AD=AE,点C、D、E在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)线段BD与线段CE的关系为________(数量关系和位置关系),请说明理由.
25.综合与探究:问题情景:如图1所示,已知,在△ABC中,AC=BA,∠ACB=90°,AD是△ABC的中线,过点C作CE⊥AD,垂足为M,且交AB于点E.
(1)(探究一)小虎通过度量发现∠BCE=∠CAD,请你帮他说明理由;
(2)(探究二)小明在图中添加了一条线段CN,且CN平分∠ACB交AD于点N,如图2所示,即可得CN=BE,符合题意吗?请说明理由;
(3)(探究三)小刚在(2)的基础上,连接DE,如图3所示,又发现了一组全等三角形,你能发现吗?请找出来,并说明理由.
答案
一、选择题
1.解:A、∵4cm+3cm=7cm,∴不能构成三角形,故本选项错误;
B、∵2cm+2.5cm=4.5cm<5cm,∴不能构成三角形,故本选项错误;
C、∵4.5cm+5cm=9.5cm<10cm,∴不能构成三角形,故本选项错误;
D、∵8cm-7cm<9cm<7cm+8cm,∴能构成三角形,故本选项正确.
故答案为:D.
2.解:A.命题是表示肯定与否定的语句,
延长线段
到
是作法,没有肯定和否定
故答案为:A不是命题,
B.锐角都相等吗是疑问句,不是肯定句或否定句,
故答案为:B不是命题;
C.
过点
作直线
,是作图语言,不是肯定或否定句,
故答案为:C不是命题;
D.垂线段最短是肯定句,是命题.
故答案为:D.
3.解:如图,
∵直线m∥n,∠1=40°,
∴∠4=∠1=40°,
∵∠3=∠2+∠2,∠2=30°,
∴∠3=30°+40°=70°,
故答案为:B.
4.∵△ABC≌△DEF,∠A=63°,∠B=70°
∴∠A=∠D=63°,∠B=∠DEF=70°
根据三角形的内角和可得∠F=180°-63°-70°=47°
故答案为:A.
5.解:由作法得DE垂直平分AB,
∴NA=NB.
故答案为:B.
6.解:由图知,甲、乙两位同学分别用尺规作图法作∠AOB的平分线OC,则他们两人的作图方法甲错误,乙正确,
故答案为:C.
7.解:由题意可知
在
中
∴
(SSS)
∴
∴
就是
的平分线
故答案为:D
8.解:∵DE是△ABC的边BC的垂直平分线,
∴BD=DC
∴AB=AD+BD=AD+DC=9
∵AC=6
∴△ACD的周长=AD+DC+AC=9+6=15
故答案为:C
9.解:∵
,∴
,故A选项正确;
∵
,
∴
,
∵
,
∴
,故B选项正确;
,故C选项正确;
∵
,
∴EF=BE,故D选项错误,
故答案为:D.
10.解:设
,
∵∠EBD=∠EDB,
∴
,
∵DF平分∠EDC,
∴
,
∴
,
∵
,∠A=78°,
∴
,
解得
,
故答案为:B.
二、填空题
11.解:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS),AB=DE=800
m.答:A
,B之间的距离为800m.故答案是800.
12.解:如图,
∵m∥n,即DE∥AB,
∴∠EDA+∠DAB=180°,
即∠1+∠CDA+∠DAC+∠CAB=180°,
∵∠CDA=90°,∠DAC=45°,∠CAB=30°,
∴∠1=180°
90°
45°
30°=15°.
故答案为:15°.
13.解:过点F作FG∥DE
∵BC∥DE
,
FG∥DE
∴BC∥FG∥DE
∴∠ABC=∠GFB=30°,∠DEF=∠GFE=45°
∴∠1=∠GFB+∠GFE=75°
故答案为:75°.
14.解:根据“如果”后面接的部分是题设,“那么”后面解的部分是结论可得:两直线平行,
同旁内角互补”改写成“如果……,那么……”的形式为:如果两条平行线被第三条直线所截,那么截得的同旁内角互补.
故答案是:如果两条平行线被第三条直线所截,那么截得的同旁内角互补.
15.解:∵OC平分∠AOB,点P在OC上,且PD⊥OA于D,PE⊥OB于E,PD=3cm,
∴PE=PD=3.
故答案为:3.
16.解:作
于E
,
如图,
由作法得AP平分∠BAC
,
∴
,
∴△ABD的面积=
.
故答案为:30.
17.解:
,
,
即
,
在
和
中,
,
∴△ACE≌△BCD(SAS)
,
,
在
中,
,
在
中,
.
故答案为:140°
18.解:∵PM垂直平分AC,PN垂直平分AB,
∴∠PMA=∠PNA=90°,∠BAC=120°
∴∠P=360°-90°-90°-120°=60°,①说法符合题意;
∵∠BAC=120°,
∴∠B+∠C=180°-120°=60°,
∵PM垂直平分AC,PN垂直平分AB,
∴EC=EA,FB=FA,
∴∠EAC=∠C,∠FAB=∠B,
∴∠EAF=∠BAC-∠EAC-∠FAB=∠BAC-(∠B+∠C)=120°-60°=60°,
∴
∠EAF=∠B+∠C,②说法符合题意;
△ABC不一定是等腰三角形,
∴PE与PF的大小无法确定,③说法不符合题意;
连接PC、PA、PB
,
?
∵PM垂直平分AC
,
PN垂直平分AB
,
∴PC=PA
,
PB=PA
,
∴PB=PC
,
即点P到点B和点C的距离相等,④说法符合题意,
故答案为:①②④.
三、解答题
19.
解:∵∠A=38°,∠B=70°,
∴∠BAC=180°﹣∠A﹣∠B=180°﹣38°﹣70°=72°,
∵CE平分∠ACB,
∴∠ACE=
∠ACB=
×72°=36°,
∵CD⊥AB,
∴∠ACD=90°﹣∠A=90°﹣38°=52°,
∴∠DCE=∠ACD﹣∠ACE=52°﹣36°=16°,
∵DP⊥CE,
∴∠CDP=90°﹣∠DCE=90°﹣16°=74°.
20.
解:如图,△ABC即为所求.
21.
证明:由图可知:
,
,
∵
,
∴
,
在
和
中:
,
∴
22.
解:如图,
∵∠1+∠2=180°(已知),
又∵∠1+∠4=180°(平角定义),
∴∠2=∠4(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行
),
∴∠3=∠ADE(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴
∠ADE=∠B(等量代换),
∴BC∥DE(同位角相等,两直线平行),
∴∠DEC+∠C=180°(两直线平行,同旁内角互补),
23.
(1)证明:
,
,
在
和
中,
(2)解:由(1)得
∴
24.
(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD,∴∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
(2)解:BD=CE,BD⊥CE
,理由如下:
由(1)知,△BAD≌△CAE,BD=CE,∠BDA=∠E,
∴∠E+∠ADE=
90°,
∴∠BDA+∠ADE=∠BDE=90°,即BD⊥CE.
25.
(1)证明:如图1中,
,
,
,
,
,
.
(2)结论:
符合题意.
理由:如图2中,
平分
,
,
,
,
,
,
在
和
中,
,
,
.
(3)结论:
.
理由:
是
的中点,
,
在
和
中,
,
.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
