2.2 算法的控制结构 课件(共18张PPT)
文档属性
| 名称 | 2.2 算法的控制结构 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-09-16 13:28:21 | ||
图片预览





文档简介
(共18张PPT)
2.2
算法控制结构
上节回顾
1.算法的概念
解决问题或完成任务的方法与步骤
为了解决问题而需要让计算机有序执行的、无歧义的、有限步骤的集合
2.算法的特征
有穷性;可行性;确定性;0个或多个输入;1个或多个输出;
3.算法的描述
自然语言、流程图、伪代码
即使很复杂的积木作品,都是由最基本的积木块(不妨称为基本结构)通过各种组合构成的。类似地,无论内容怎样复杂、功能如何强大的算法,也都由基本的结构组合而成,这些基本的结构称为算法的控制结构。
算法的控制结构有三种,即顺序结构、分支结构和循环结构。
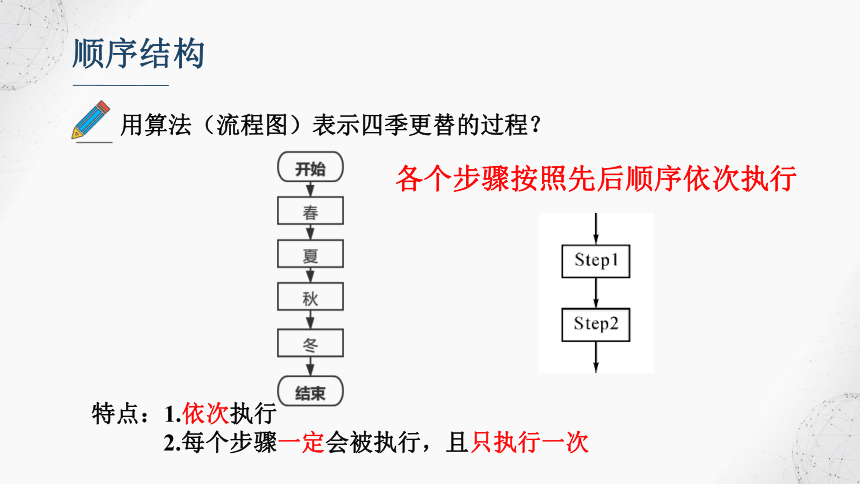
顺序结构
四季更替
顺序结构
各个步骤按照先后顺序依次执行
特点:1.依次执行
2.每个步骤一定会被执行,且只执行一次
用算法(流程图)表示四季更替的过程?
练习1:计算并输出S=1+2+3+4+5+6。
方法1:逐一相加
①计算1+2,得3;
②用①步的结果3与3相加得6;
③用②步的结果6与4相加得10;
④用③步的结果10与5相加得15;
⑤用④步的结果15与6相加得21.
方法2:运用数学公式
计算:s=n×(n+1)/2
输出:s
的值
s=0,n=6
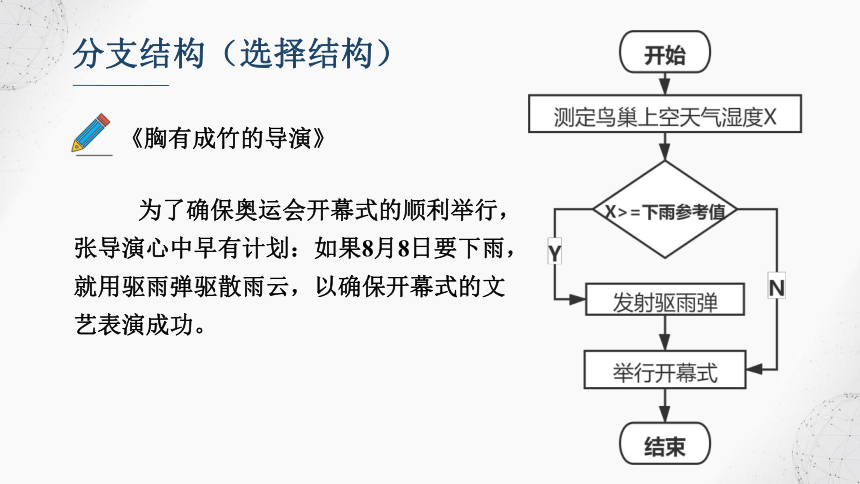
分支结构(选择结构)
《胸有成竹的导演》
为了确保奥运会开幕式的顺利举行,张导演心中早有计划:如果8月8日要下雨,就用驱雨弹驱散雨云,以确保开幕式的文艺表演成功。
分支结构(选择结构)
根据条件判断选择不同的分支执行:
条件为真时执行Y指向的语句,否则执行N指向的语句。
选择结构中,必有一个分支被执行,其余分支不执行。
分支结构(选择结构)
语句块
T
F
条件表达式是否为真?
当表达式为真时,
执行语句块;
否则什么都不执行;
当表达式为真时,
执行语句块1;
否则(表达式为假)
执行语句块2;
单分支结构
双分支结构
分支结构(选择结构)
特点:条件判断选择不同分支,一次只执行一个分支,其余分支不执行
当<表达式1>条件成立时,执行<语句块1>,
本结构结束。若为假,则判断<表达式2>,依此类推。直到找到一个为真的条件时,才执行相应的语句块,
本结构结束。
循环结构
飞逝的岁月
循环结构
对某个条件进行判断,当符合条件时,执行Y指向的语句(循环体),然后返回重新判断这个条件,当符合条件时,再次执行循环体。重复上述过程,直到不符合条件,则跳出循环,执行循环体后面的指令。
若循环条件始终满足?
算法无限循环,违背有穷性
练习:在抽屉寻找东西的过程
练习:求100之内的数之和s=1+2+3+….+100。
S1=0+1
S2=0+1+2
S3=0+1+2+3
S99=0+1+2+3+……+99
S100=0+1+2+3+……+99+100
有什么规律?
Sn=Sn-1+n
n从1到100
1
S从S1到S100
扩展:求100之内的偶数之和s=2+4+6+….+100。
分支or循环
判断依据:分支结构:条件是否成立只判断1次
循环结构:条件是否成立往往判断多次
分支结构
循环结构
分支结构
循环结构
用算法解决问题
用算法求解圆的面积,已知圆的半径r,圆的面积s
明确要素:
r
s
明确数学函数:
具体算法设计:
1.输入半径r
2.s←
3.输出面积s
描述算法:
输入r
s←
输出s
用算法解决问题
1.抽象与建模
a.提炼核心要素并加以确定或假设
b.用数学符号描述解决问题的计算模型
2.设计算法
a.输入数据
b.处理数据
c.输出处理结果
3.描述算法
自然语言、流程图、伪代码、计算机程序设计语言
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
用算法解决问题
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
明确要素:
明确数学函数:
具体算法设计:
描述算法:
里程数x
费用f
1.输入里程数x
2.若0若3若x>=10,f=10+7
2+3(x-10)
3.输出费用f
2.2
算法控制结构
上节回顾
1.算法的概念
解决问题或完成任务的方法与步骤
为了解决问题而需要让计算机有序执行的、无歧义的、有限步骤的集合
2.算法的特征
有穷性;可行性;确定性;0个或多个输入;1个或多个输出;
3.算法的描述
自然语言、流程图、伪代码
即使很复杂的积木作品,都是由最基本的积木块(不妨称为基本结构)通过各种组合构成的。类似地,无论内容怎样复杂、功能如何强大的算法,也都由基本的结构组合而成,这些基本的结构称为算法的控制结构。
算法的控制结构有三种,即顺序结构、分支结构和循环结构。
顺序结构
四季更替
顺序结构
各个步骤按照先后顺序依次执行
特点:1.依次执行
2.每个步骤一定会被执行,且只执行一次
用算法(流程图)表示四季更替的过程?
练习1:计算并输出S=1+2+3+4+5+6。
方法1:逐一相加
①计算1+2,得3;
②用①步的结果3与3相加得6;
③用②步的结果6与4相加得10;
④用③步的结果10与5相加得15;
⑤用④步的结果15与6相加得21.
方法2:运用数学公式
计算:s=n×(n+1)/2
输出:s
的值
s=0,n=6
分支结构(选择结构)
《胸有成竹的导演》
为了确保奥运会开幕式的顺利举行,张导演心中早有计划:如果8月8日要下雨,就用驱雨弹驱散雨云,以确保开幕式的文艺表演成功。
分支结构(选择结构)
根据条件判断选择不同的分支执行:
条件为真时执行Y指向的语句,否则执行N指向的语句。
选择结构中,必有一个分支被执行,其余分支不执行。
分支结构(选择结构)
语句块
T
F
条件表达式是否为真?
当表达式为真时,
执行语句块;
否则什么都不执行;
当表达式为真时,
执行语句块1;
否则(表达式为假)
执行语句块2;
单分支结构
双分支结构
分支结构(选择结构)
特点:条件判断选择不同分支,一次只执行一个分支,其余分支不执行
当<表达式1>条件成立时,执行<语句块1>,
本结构结束。若为假,则判断<表达式2>,依此类推。直到找到一个为真的条件时,才执行相应的语句块,
本结构结束。
循环结构
飞逝的岁月
循环结构
对某个条件进行判断,当符合条件时,执行Y指向的语句(循环体),然后返回重新判断这个条件,当符合条件时,再次执行循环体。重复上述过程,直到不符合条件,则跳出循环,执行循环体后面的指令。
若循环条件始终满足?
算法无限循环,违背有穷性
练习:在抽屉寻找东西的过程
练习:求100之内的数之和s=1+2+3+….+100。
S1=0+1
S2=0+1+2
S3=0+1+2+3
S99=0+1+2+3+……+99
S100=0+1+2+3+……+99+100
有什么规律?
Sn=Sn-1+n
n从1到100
1
S从S1到S100
扩展:求100之内的偶数之和s=2+4+6+….+100。
分支or循环
判断依据:分支结构:条件是否成立只判断1次
循环结构:条件是否成立往往判断多次
分支结构
循环结构
分支结构
循环结构
用算法解决问题
用算法求解圆的面积,已知圆的半径r,圆的面积s
明确要素:
r
s
明确数学函数:
具体算法设计:
1.输入半径r
2.s←
3.输出面积s
描述算法:
输入r
s←
输出s
用算法解决问题
1.抽象与建模
a.提炼核心要素并加以确定或假设
b.用数学符号描述解决问题的计算模型
2.设计算法
a.输入数据
b.处理数据
c.输出处理结果
3.描述算法
自然语言、流程图、伪代码、计算机程序设计语言
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
用算法解决问题
某地出租车米表进行计费,规则如下:
3公里(包括3公里)以内收起步价10元;
超过3公里但低于10公里(包括10公里)时,超过部分每公里2元;
超过10公里时,超过部分每公里3元。
明确要素:
明确数学函数:
具体算法设计:
描述算法:
里程数x
费用f
1.输入里程数x
2.若0
2+3(x-10)
3.输出费用f
