2.3.1有理数的乘法 课件(共16张PPT)
文档属性
| 名称 | 2.3.1有理数的乘法 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
2.3有理数的乘法
第1课时
浙教版
七年级上
新知导入
思考1
有理数的加法有哪几种情况?
①同号两数相加(正数+正数、负数+负数)
②异号两数相加(正数+负数)
③零与有理数相加
思考2
你觉得有理数的乘法会有哪几种情况?
①同号两数相乘(正数×正数、负数×负数)
②异号两数相乘(正数×负数)
③零与有理数相乘
类比猜想
新知探究
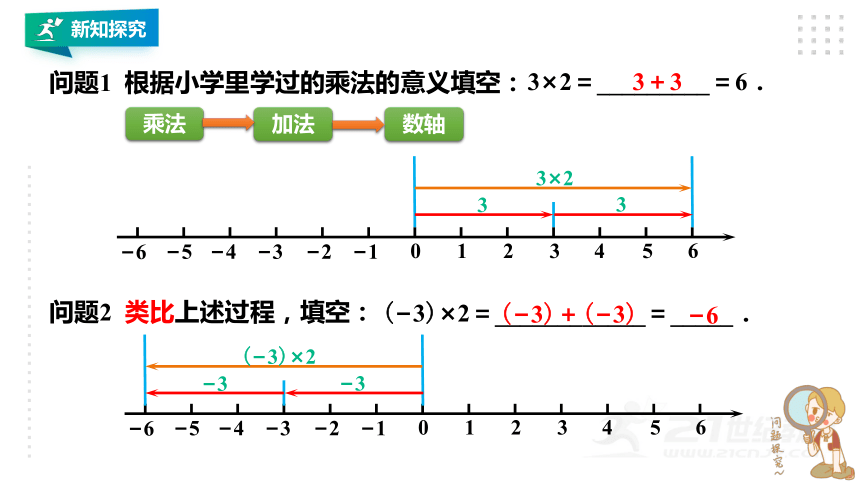
问题1
根据小学里学过的乘法的意义填空:
3×2=_________=6.
3+3
0
1
2
3
4
?1
?2
?3
?4
5
?5
6
?6
乘法
加法
3
3
3×2
问题2
类比上述过程,填空:
(?3)×2=____________=_____.
(?3)+(?3)
?6
0
1
2
3
4
?1
?2
?3
?4
5
?5
6
?6
?3
(?3)×2
?3
数轴
新知探究
做一做
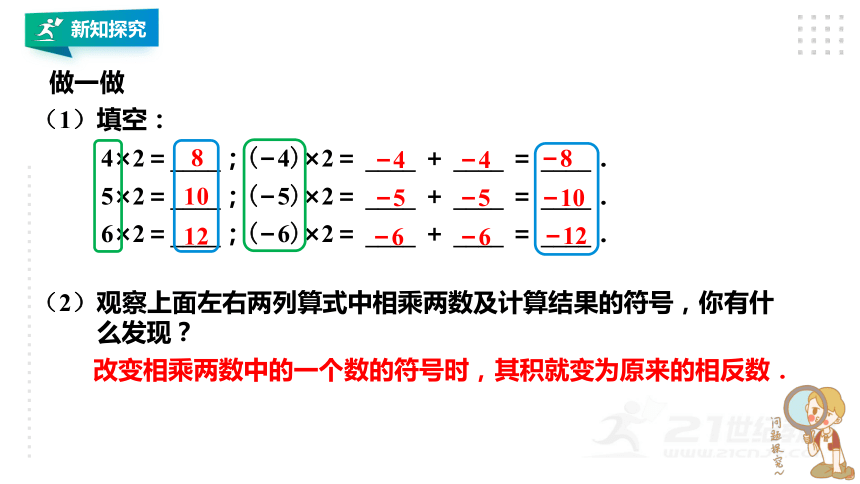
(1)填空:
4×2=____;(?4)×2=
____
+
____
=
____.
5×2=____;(?5)×2=
____
+
____
=
____.
6×2=____;(?6)×2=
____
+
____
=
____.
(2)观察上面左右两列算式中相乘两数及计算结果的符号,你有什
么发现?
8
?4
?4
?8
10
?5
?10
12
?5
?6
?6
?12
改变相乘两数中的一个数的符号时,其积就变为原来的相反数.
新知探究
(3)根据上述结论计算:
改变相乘两数中的一个数的符号时,其积就变为原来的相反数.
3×7=____,(?3)×7=
____
,3×(?7)=
____
,(?3)×(?7)=
____.
?21
21
?21
21
0×7=____,0×(?7)=
____
.
0
0
(4)由此你认为两个数相乘,积的符号与这两个数的符号有什么关系?
积的绝对值呢?
当相乘两数为同号时,积的符号为正.
当相乘两数为异号时,积的符号为负.
积的绝对值等于相乘两数绝对值的积.
定结果的符号
定结果的绝对值
当相乘两数中有一个数为零时,结果为零.
新知讲解
有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与零相乘,积为零.
练习:用“<”,“>”或“=”填空
(1)(?7)×(+3)
0.
(2)(?13)×(?7.9)
0.
(3)0×
(?
)
0.
<
>
=
例题讲解
例1
计算:
(1)
(2)(?2.5)×4
(3)(?5)×0×
(4)(?
)×(?3)
(5)(?6)×(?
)×(?4)
=1
=?(2.5×4)
=?10
=0
=+(×3)
=1
=?(6××4)
=?30
想一想
几个有理数相乘,
怎样确定积的符号?
多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
新知讲解
(?
)×(?3)
若两个有理数的乘积为1,就称这两个有理数互为倒数.
例如,
是
的倒数,
也是
的倒数.
练习:
的倒数是______
,?
?8的倒数是______
,
1的倒数是______
,
0的倒数是
1
?7
?
0没有倒数
Why?
因为任何数与0相乘,积为0,
不存在与0相乘积为1的数.
课堂练习
1
计算:
(1)
(2)
(3)
(4)(?2)×3×(?0.5)
(5)(?
)×(?
)×(?2)
(6)|?1.25|×(?8)×4
=?
=
=?
=3
=?
=?40
课堂练习
2.下列说法中,正确的是(
)
(A)0的倒数是0
(B)倒数是它本身的数是1
(C)相反数等于它本身的数是负数
(D)绝对值最小的数是0
D
3.4个有理数相乘,积的符号是负号,则这四个有理数中,正数有
(
)
(A)1个或3个
(B)1个或2个
(C)2个或4个
(D)3个或4个
A
4.把?6表示成两个整数的积,有多少种可能?把它们全部写出来.
拓展提升
如图所示为一个“数值转换机”(箭头是指数进入转换机的路径,方框
是对进入的数进行转换的转换机).
(1)当小张输入4,7这两个数时,两次输出的结果依次为___,___.
(2)这个“数值转换机”不可能输出____数.
1
2
负
课堂总结
1.有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与零相乘,积为零.
2.多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
若两个有理数的乘积为1,就称这两个有理数互为倒数.
3.倒数的定义:
板书设计
1.有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与零相乘,积为零.
2.多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
若两个有理数的乘积为1,就称这两个有理数互为倒数.
3.倒数的定义:
1.作业本1
2.3有理数的乘法(1)
2.自主练习
作业布置
https://www.21cnjy.com/help/help_extract.php
2.3有理数的乘法
第1课时
浙教版
七年级上
新知导入
思考1
有理数的加法有哪几种情况?
①同号两数相加(正数+正数、负数+负数)
②异号两数相加(正数+负数)
③零与有理数相加
思考2
你觉得有理数的乘法会有哪几种情况?
①同号两数相乘(正数×正数、负数×负数)
②异号两数相乘(正数×负数)
③零与有理数相乘
类比猜想
新知探究
问题1
根据小学里学过的乘法的意义填空:
3×2=_________=6.
3+3
0
1
2
3
4
?1
?2
?3
?4
5
?5
6
?6
乘法
加法
3
3
3×2
问题2
类比上述过程,填空:
(?3)×2=____________=_____.
(?3)+(?3)
?6
0
1
2
3
4
?1
?2
?3
?4
5
?5
6
?6
?3
(?3)×2
?3
数轴
新知探究
做一做
(1)填空:
4×2=____;(?4)×2=
____
+
____
=
____.
5×2=____;(?5)×2=
____
+
____
=
____.
6×2=____;(?6)×2=
____
+
____
=
____.
(2)观察上面左右两列算式中相乘两数及计算结果的符号,你有什
么发现?
8
?4
?4
?8
10
?5
?10
12
?5
?6
?6
?12
改变相乘两数中的一个数的符号时,其积就变为原来的相反数.
新知探究
(3)根据上述结论计算:
改变相乘两数中的一个数的符号时,其积就变为原来的相反数.
3×7=____,(?3)×7=
____
,3×(?7)=
____
,(?3)×(?7)=
____.
?21
21
?21
21
0×7=____,0×(?7)=
____
.
0
0
(4)由此你认为两个数相乘,积的符号与这两个数的符号有什么关系?
积的绝对值呢?
当相乘两数为同号时,积的符号为正.
当相乘两数为异号时,积的符号为负.
积的绝对值等于相乘两数绝对值的积.
定结果的符号
定结果的绝对值
当相乘两数中有一个数为零时,结果为零.
新知讲解
有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与零相乘,积为零.
练习:用“<”,“>”或“=”填空
(1)(?7)×(+3)
0.
(2)(?13)×(?7.9)
0.
(3)0×
(?
)
0.
<
>
=
例题讲解
例1
计算:
(1)
(2)(?2.5)×4
(3)(?5)×0×
(4)(?
)×(?3)
(5)(?6)×(?
)×(?4)
=1
=?(2.5×4)
=?10
=0
=+(×3)
=1
=?(6××4)
=?30
想一想
几个有理数相乘,
怎样确定积的符号?
多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
新知讲解
(?
)×(?3)
若两个有理数的乘积为1,就称这两个有理数互为倒数.
例如,
是
的倒数,
也是
的倒数.
练习:
的倒数是______
,?
?8的倒数是______
,
1的倒数是______
,
0的倒数是
1
?7
?
0没有倒数
Why?
因为任何数与0相乘,积为0,
不存在与0相乘积为1的数.
课堂练习
1
计算:
(1)
(2)
(3)
(4)(?2)×3×(?0.5)
(5)(?
)×(?
)×(?2)
(6)|?1.25|×(?8)×4
=?
=
=?
=3
=?
=?40
课堂练习
2.下列说法中,正确的是(
)
(A)0的倒数是0
(B)倒数是它本身的数是1
(C)相反数等于它本身的数是负数
(D)绝对值最小的数是0
D
3.4个有理数相乘,积的符号是负号,则这四个有理数中,正数有
(
)
(A)1个或3个
(B)1个或2个
(C)2个或4个
(D)3个或4个
A
4.把?6表示成两个整数的积,有多少种可能?把它们全部写出来.
拓展提升
如图所示为一个“数值转换机”(箭头是指数进入转换机的路径,方框
是对进入的数进行转换的转换机).
(1)当小张输入4,7这两个数时,两次输出的结果依次为___,___.
(2)这个“数值转换机”不可能输出____数.
1
2
负
课堂总结
1.有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与零相乘,积为零.
2.多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
若两个有理数的乘积为1,就称这两个有理数互为倒数.
3.倒数的定义:
板书设计
1.有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与零相乘,积为零.
2.多个不为零的有理数相乘,积的符号由负因数的个数确定.
负因数的个数为奇数时,积为负;负因数的个数为偶数时,积为正.
若两个有理数的乘积为1,就称这两个有理数互为倒数.
3.倒数的定义:
1.作业本1
2.3有理数的乘法(1)
2.自主练习
作业布置
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
