2021-2022浙教版数学八上第一章 三角形的初步知识常考必刷题(含解析)
文档属性
| 名称 | 2021-2022浙教版数学八上第一章 三角形的初步知识常考必刷题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 16:05:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2021-2022浙教版数学八上第一章三角形的初步认识常考必刷题
时间120分钟
满分120分
一.选择题(每小题3分,共36分)
1.(2021春?靖江市期末)下列各组图形中,表示AD是△ABC中BC边的高的图形为( )
A.
B.
C.
D.
2.(2021春?金坛区期末)若一个三角形的两边长分别是3cm,6cm,则它的第三边的长可以是( )
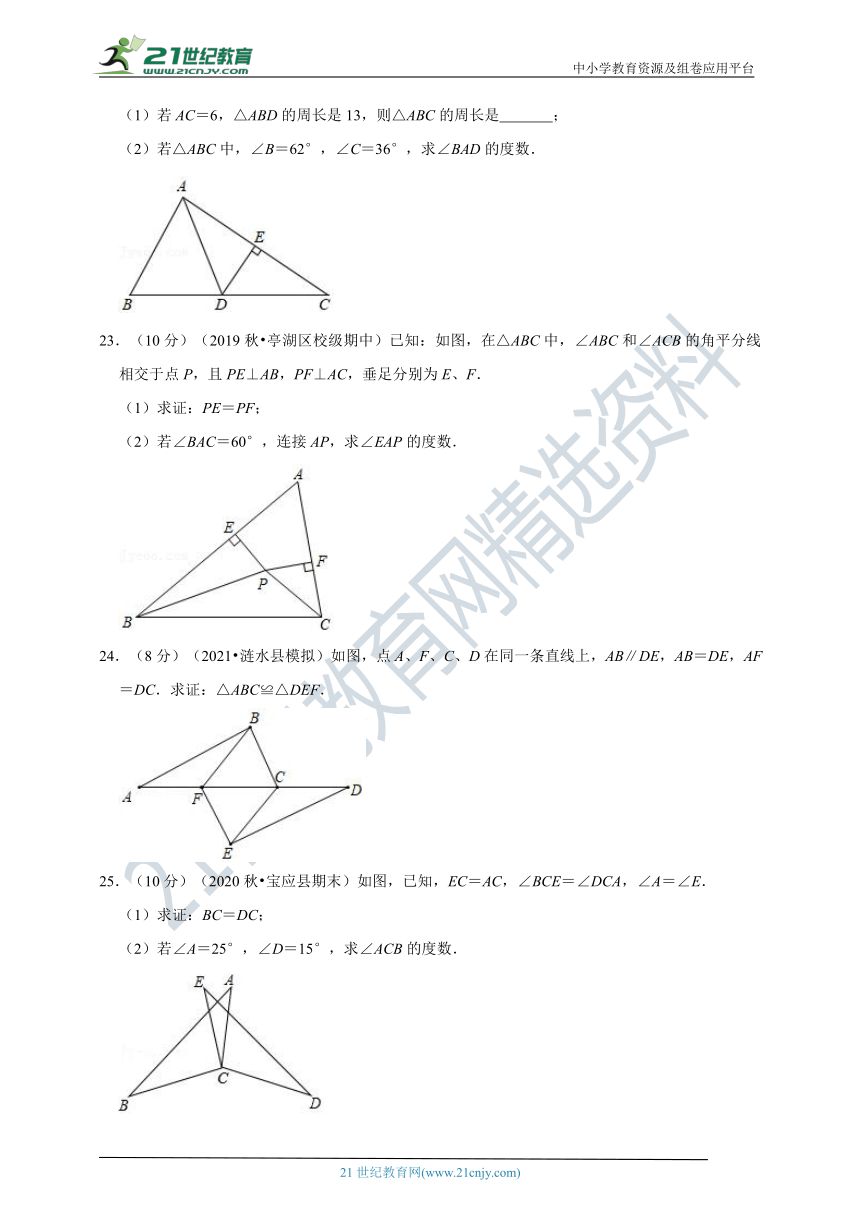
A.3cm
B.6cm
C.9cm
D.12cm
3.(2021春?崇川区校级月考)如图,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( )
A.50°
B.60°
C.30°
D.40°
4.(2021?盐城)将一副三角板按如图方式重叠,则∠1的度数为( )
A.45°
B.60°
C.75°
D.105°
5.(2021春?广陵区校级期中)下列命题中是真命题的是( )
A.相等的角是对顶角
B.如果a3=b3,那么a=b
C.三角形的一个外角等于两个内角之和
D.内错角相等
6.(2020秋?宝应县期中)七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )
A.甲、乙、丙、丁
B.甲、丙、乙、丁
C.甲、丁、乙、丙
D.甲、丙、丁、乙
7.(2021春?工业园区期末)如图,若△ABC≌△ADE,则下列结论中不一定成立的是( )
A.∠ACB=∠DAC
B.AC=AE
C.BC=DE
D.∠BAD=∠CDE
8.(2021春?泰兴市期末)下列所给的四组条件中,能作出唯一三角形的是( )
A.AB=2cm,BC=6cm,AC=3cm
B.BC=3cm,AC=5cm,∠B=90°
C.∠A=∠B=∠C=60°
D.AB=4cm,AC=6cm,∠C=30°
9.(2021春?泰兴市期末)如图所示,AP平分∠BAC,点M,N分别在边AB,AC上,如果添加一个条件,即可推出AM=AN,那么下面条件不正确的是( )
A.PM=PN
B.∠APM=∠APN
C.MN⊥AP
D.∠AMP=∠ANP
10.(2021?淮安)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2
B.4
C.6
D.8
11.(2021春?洪江市期末)如图,在△ABC中,∠B=90°,AD平分∠BAC,BC=10,CD=6,则点D到AC的距离为( )
A.4
B.6
C.8
D.10
12.(2019秋?扎鲁特旗期末)如图,用尺规作一个角等于已知角,其理论依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
二.填空题(每小题4分,共24分)
13.(2021?淮安)一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是
.
14.(2021?常州)如图,在△ABC中,点D、E分别在BC、AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED=
°.
15.(2020?泰州)如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为
.
16.(2021春?南京期中)命题“垂直于同一条直线的两条直线平行”写成“如果…,那么…”的形式为:如果
,那么
.
17.(2021?东城区二模)如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是
.
18.(2020秋?江都区期末)如图,点A,B,C在同一条直线上,∠A=∠DBE=∠C=90°,请你只添加一个条件,使得△DAB≌△BCE.你添加的条件是
.(要求:不再添加辅助线,只需填一个答案即可)
三.解答题(共60分)
19.(6分)(2017春?辉县市期末)如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
20.(6分)(2020春?相城区期中)若a,b,c是△ABC三边的长,化简:|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a﹣b|.
21.(10分)(2020秋?前郭县期末)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.
(1)若∠BAC=70°,求:∠BOC的度数;
(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)
22.(10分)(2021春?吴中区月考)如图,在△ABC中,DE是AC的垂直平分线.
(1)若AC=6,△ABD的周长是13,则△ABC的周长是
;
(2)若△ABC中,∠B=62°,∠C=36°,求∠BAD的度数.
23.(10分)(2019秋?亭湖区校级期中)已知:如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,垂足分别为E、F.
(1)求证:PE=PF;
(2)若∠BAC=60°,连接AP,求∠EAP的度数.
24.(8分)(2021?涟水县模拟)如图,点A、F、C、D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:△ABC≌△DEF.
25.(10分)(2020秋?宝应县期末)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
(1)求证:BC=DC;
(2)若∠A=25°,∠D=15°,求∠ACB的度数.
2021-2022浙教版数学八上第一章三角形的初步认识常考必刷题
参考答案与试题解析
一.选择题
1.(2021春?靖江市期末)下列各组图形中,表示AD是△ABC中BC边的高的图形为( )
A.
B.
C.
D.
【分析】根据高的定义:”过三角形的顶点向对边作垂线,顶点和垂足之间的线段叫做三角形的高线“解答.
【解答】解:△ABC的高AD是过顶点A与BC垂直的线段,只有D选项符合.
故选:D.
2.(2021春?金坛区期末)若一个三角形的两边长分别是3cm,6cm,则它的第三边的长可以是( )
A.3cm
B.6cm
C.9cm
D.12cm
【分析】首先设第三边长为xcm,根据三角形的三边关系可得6﹣3<x<6+3,再解不等式即可.
【解答】解:设第三边长为xcm,根据三角形的三边关系可得:
6﹣3<x<6+3,
解得:3<x<9,
故选:B.
3.(2021春?崇川区校级月考)如图,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( )
A.50°
B.60°
C.30°
D.40°
【分析】先根据∠1=50°由平行线的性质求出∠A的度数,根据直角三角形两锐角互余的性质即可求出∠B的度数.
【解答】解:∵EF∥AB,
∴∠A=∠1=50°,
∵△ABC是直角三角形,
∴∠B=90°﹣∠A=90°﹣50°=40°.
故选:D.
4.(2021?盐城)将一副三角板按如图方式重叠,则∠1的度数为( )
A.45°
B.60°
C.75°
D.105°
【分析】直接利用一副三角板的内角度数,再结合三角形外角的性质得出答案.
【解答】解:根据三角板的度数知,∠ABC=∠ACB=45°,∠DBC=30°,
∴∠1=∠DBC+∠ACB=30°+45°=75°,
故选:C.
5.(2021春?广陵区校级期中)下列命题中是真命题的是( )
A.相等的角是对顶角
B.如果a3=b3,那么a=b
C.三角形的一个外角等于两个内角之和
D.内错角相等
【分析】根据对顶角的定义、等式的性质、三角形的角及平行线的性质判断即可.
【解答】解:A、相等的角不一定是对顶角,原命题是假命题;
B、如果a3=b3,那么a=b,是真命题;
C、三角形的一个外角等于与它不相邻的两个内角之和,原命题是假命题;
D、两直线平行,内错角相等,原命题是假命题;
故选:B.
6.(2020秋?宝应县期中)七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )
A.甲、乙、丙、丁
B.甲、丙、乙、丁
C.甲、丁、乙、丙
D.甲、丙、丁、乙
【分析】因为他们每人只猜对一半,可以先假设明明说“甲得第一”是正确的,由此推导:分别分析得出所有的可能即可.
【解答】解:因为他们每人只猜对一半,
可以先假设明明说“甲得第一”是正确的,由此推导:
明明:甲得第一→文文:丁得第四→凡凡:丙得第二→乙得第三,成立;
若假设明明说“乙得第二”是正确的,由此进行推导:
明明:乙得第二→文文:丁得第四→凡凡:丙得第二,矛盾.
所以甲、乙、丙、丁的名次顺序为甲、丙、乙、丁.
故选:B.
7.(2021春?工业园区期末)如图,若△ABC≌△ADE,则下列结论中不一定成立的是( )
A.∠ACB=∠DAC
B.AC=AE
C.BC=DE
D.∠BAD=∠CDE
【分析】根据翻三角形全等的性质一一判断即可.
【解答】解:∵△ABC≌△ADE,
∴AD=AB,AE=AC,BC=DE,∠ABC=∠ADE,
∴∠BAD=∠CAE,
∵AD=AB,
∴∠ABD=∠ADB,
∴∠BAD=180°﹣∠ABD﹣∠ADB,
∴∠CDE=180°﹣∠ADB﹣ADE,
∵∠ABD=∠ADE,
∴∠BAD=∠CDE
故B、C、D选项不符合题意,
故选:A.
8.(2021春?泰兴市期末)下列所给的四组条件中,能作出唯一三角形的是( )
A.AB=2cm,BC=6cm,AC=3cm
B.BC=3cm,AC=5cm,∠B=90°
C.∠A=∠B=∠C=60°
D.AB=4cm,AC=6cm,∠C=30°
【分析】根据三角形三边的关系对A进行判断;根据全等三角形的判定方法对B、C、D进行判断.
【解答】解:A、因为AB+AC<BC,三条线段不能组成三角形,所以A选项不符合题意;
B、BC=3cm,AC=5cm,∠B=90°,根据“HL”可判断此三角形为唯一三角形,所以B选项符合题意;
C、利用∠A=∠B=∠C=60°不能确定三角形的大小,所以C选项不符合题意;
D、利用AB=4cm,AC=6cm,∠C=30°可画出两三角形,所以D选项不符合题意.
故选:B.
9.(2021春?泰兴市期末)如图所示,AP平分∠BAC,点M,N分别在边AB,AC上,如果添加一个条件,即可推出AM=AN,那么下面条件不正确的是( )
A.PM=PN
B.∠APM=∠APN
C.MN⊥AP
D.∠AMP=∠ANP
【分析】根据已知条件结合三角形全等的判定方法,验证各选项提供的条件是否能证△APM≌△APN即可.
【解答】解:∵AP平分∠BAC,∴∠BAP=∠CAP,
A、由∠BAP=∠CAP,PM=PN,AP=AP,不能判定△APM≌△APN,
∴不推出AM=AN,故选项A符合题意;
B、由∠BAP=∠CAP,AP=AP,∠APM=∠APN,能判定△APM≌△APN(ASA),
∴AM=AN,故选项B不符合题意;
C、∵MN⊥AP,
∴∠APM=∠APN=90°,
又由∠BAP=∠CAP,AP=AP,能判定△APM≌△APN(ASA),
∴AM=AN,故选项C不符合题意;
D、由∠BAP=∠CAP,AP=AP,∠AMP=∠ANP,能判定△APM≌△APN(AAS),
∴AM=AN,故选项D不符合题意;
故选:A.
10.(2021?淮安)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2
B.4
C.6
D.8
【分析】根据线段的垂直平分线的性质得到EB=EA=4,结合图形计算,得到答案.
【解答】解:∵DE是AB的垂直平分线,AE=4,
∴EB=EA=4,
∴BC=EB+EC=4+2=6,
故选:C.
11.(2021春?洪江市期末)如图,在△ABC中,∠B=90°,AD平分∠BAC,BC=10,CD=6,则点D到AC的距离为( )
A.4
B.6
C.8
D.10
【分析】由条件可先求得BD的长,再根据角平分线的性质可知D到AC的距离等于BD,可得到答案.
【解答】解:∵BC=10,CD=6,
∴BD=BC﹣CD=10﹣6=4,
△ABC中,∠B=90°,AD平分∠BAC,
∴点D到AC的距离=BD=4.
故选:A.
12.(2019秋?扎鲁特旗期末)如图,用尺规作一个角等于已知角,其理论依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
【分析】根据作图过程以及全等三角形的判定方法进行判断解答.
【解答】解:根据作图过程可知,
OC=O′C′,OD=O′D′,CD=C′D′,
∴利用的是三边对应相等,两三角形全等,
即作图原理是SSS.
故选:A.
二.填空题
13.(2021?淮安)一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是
4 .
【分析】利用三角形三边关系定理,先确定第三边的范围,再根据第三边是偶数这一条件,求得第三边的值.
【解答】解:设第三边为a,根据三角形的三边关系知,
4﹣1<a<4+1,即3<a<5,
又∵第三边的长是偶数,
∴a为4.
故答案为:4.
14.(2021?常州)如图,在△ABC中,点D、E分别在BC、AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED= 100 °.
【分析】利用平行线的性质以及三角形的内角和定理解决问题即可.
【解答】解:在△ABC中,∠BAC+∠B+∠C=180°,
∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵DE∥AB,
∴∠A+∠AED=180°,
∴∠AED=180°﹣80°=100°.
故答案为:100.
15.(2020?泰州)如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为 140° .
【分析】根据三角形外角性质求出求出∠DFB,再根据三角形外角性质求出∠α即可.
【解答】解:如图,
∵∠B=30°,∠DCB=65°,
∴∠DFB=∠B+∠DCB=30°+65°=95°,
∴∠α=∠D+∠DFB=45°+95°=140°,
故答案为:140°.
16.(2021春?南京期中)命题“垂直于同一条直线的两条直线平行”写成“如果…,那么…”的形式为:如果 两条直线垂直于同一条直线 ,那么 这两条直线互相平行 .
【分析】把命题的题设部分写在如果的后面,把结论部分写在那么的后面.
【解答】解:命题“垂直于同一条直线的两条直线平行”改写成“如果…,那么…”的形式为:如果两条直线垂直于同一条直线,那么这两条直线互相平行,
故答案为:两条直线垂直于同一条直线,那么这两条直线相互平行.
17.(2021?东城区二模)如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是 BC=DF(答案不唯一) .
【分析】根据全等三角形的判定方法可以由SSS证明△ABC≌△EDF.
【解答】解:添加BC=DF.
∵AD=BE,
∴AD+DB=BE+BD,
∴AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS),
故答案为:BC=DF(答案不唯一).
18.(2020秋?江都区期末)如图,点A,B,C在同一条直线上,∠A=∠DBE=∠C=90°,请你只添加一个条件,使得△DAB≌△BCE.你添加的条件是 DB=BE(答案不唯一) .(要求:不再添加辅助线,只需填一个答案即可)
【分析】此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.
【解答】解:添加的条件是DB=BE,
理由是:∵∠A=∠DBE=90°,
∴∠D+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠D=∠CBE,
在△DAB和△BCE中,
,
∴△DAB≌△BCE(AAS),
故答案为:DB=BE(答案不唯一).
三.解答题
19.(2017春?辉县市期末)如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
【分析】根据直角三角形两锐角互余求出∠AED,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE,然后根据角平分线的定义求出∠BAC,再利用三角形的内角和定理列式计算即可得解.
【解答】解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
20.(2020春?相城区期中)若a,b,c是△ABC三边的长,化简:|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a﹣b|.
【分析】根据三角形的三边关系判断出a+b﹣c,b﹣a﹣c及c﹣a﹣b的符号,再去绝对值符号,合并同类项即可.
【解答】解:∵a、b、c是△ABC的三边的长,
∴a+b﹣c>0,b﹣a﹣c<0,c﹣a﹣b<0,
∴原式=a+b﹣c﹣b+a+c+c﹣a﹣b=a﹣b+c.
21.(2020秋?前郭县期末)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.
(1)若∠BAC=70°,求:∠BOC的度数;
(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)
【分析】(1)根据三角形的角平分线定义和三角形的内角和定理求出∠OBC+∠OCB的度数,再根据三角形的内角和定理即可求出∠BOC的度数;
(2)根据三角形外角平分线的性质可得∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB);根据三角形内角和定理可得∠BDC=90°﹣∠A.
【解答】解:(1)∵OB、OC分别是∠ABC和∠ACB的角平分线,
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB),
∵∠A=70°,
∴∠OBC+∠OCB=(180°﹣70°)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣55°
=125°;
(2)∠BDC=90°﹣∠A.
理由如下:
∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,
∴∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB),
由三角形内角和定理得,∠BDC=180°﹣∠BCD﹣∠DBC,
=180°﹣[∠A+(∠A+∠ABC+∠ACB)],
=180°﹣(∠A+180°),
=90°﹣∠A;
22.(2021春?吴中区月考)如图,在△ABC中,DE是AC的垂直平分线.
(1)若AC=6,△ABD的周长是13,则△ABC的周长是 19 ;
(2)若△ABC中,∠B=62°,∠C=36°,求∠BAD的度数.
【分析】(1)根据线段垂直平分线的性质得到DA=DC,根据三角形的周长公式计算,得到答案;
(2)根据三角形内角和定理求出∠BAC,根据等腰三角形的性质求出∠DAC,计算即可.
【解答】解:(1)∵DE是AC的垂直平分线,
∴DA=DC,
∵△ABD的周长是13,
∴AB+AD+BD=AB+DC+BD=AB+BC=13,
∴△ABC的周长=AB+BC+AC=13+6=19,
故答案为:19;
(2)在△ABC中,∠B=62°,∠C=36°,
则∠BAC=180°﹣∠B﹣∠C=82°,
∵DA=DC,
∴∠DAC=∠C=36°,
∴∠BAD=∠BAC﹣∠DAC=82°﹣36°=46°.
23.(2019秋?亭湖区校级期中)已知:如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,垂足分别为E、F.
(1)求证:PE=PF;
(2)若∠BAC=60°,连接AP,求∠EAP的度数.
【分析】(1)过点P作PD⊥BC于D,可得PD=PE=PF;
(2)可得AP是∠BAC的平分线,则∠EAP可求出.
【解答】解:(1)过点P作PD⊥BC于D,
∵∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,
∴PD=PE,PD=PF,
∴PE=PF;
(2)∵PE=PF,PE⊥AB,PF⊥AC,
∴AP平分∠BAC,
∵∠BAC=60°,
∴∠EAP==30°.
24.(2021?涟水县模拟)如图,点A、F、C、D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:△ABC≌△DEF.
【分析】根据平行线的性质得出∠A=∠D,求出AC=DF,再根据全等三角形的判定定理推出即可.
【解答】证明:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF+CF=DC+CF,
即AC=DF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
25.(2020秋?宝应县期末)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
(1)求证:BC=DC;
(2)若∠A=25°,∠D=15°,求∠ACB的度数.
【分析】(1)根据ASA证明△BCA≌△DCE,进而利用全等三角形的性质解答即可;
(2)根据全等三角形的性质解答即可.
【解答】证明:(1)∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ECA,
即∠BCA=∠DCE,
在△BCA和△DCE中,
,
∴△BCA≌△DCE(ASA),
∴BC=DC;
(2)∵△BCA≌△DCE,
∴∠B=∠D=15°,
∵∠A=25°,
∴∠ACB=180°﹣∠A﹣∠B=140°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2021-2022浙教版数学八上第一章三角形的初步认识常考必刷题
时间120分钟
满分120分
一.选择题(每小题3分,共36分)
1.(2021春?靖江市期末)下列各组图形中,表示AD是△ABC中BC边的高的图形为( )
A.
B.
C.
D.
2.(2021春?金坛区期末)若一个三角形的两边长分别是3cm,6cm,则它的第三边的长可以是( )
A.3cm
B.6cm
C.9cm
D.12cm
3.(2021春?崇川区校级月考)如图,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( )
A.50°
B.60°
C.30°
D.40°
4.(2021?盐城)将一副三角板按如图方式重叠,则∠1的度数为( )
A.45°
B.60°
C.75°
D.105°
5.(2021春?广陵区校级期中)下列命题中是真命题的是( )
A.相等的角是对顶角
B.如果a3=b3,那么a=b
C.三角形的一个外角等于两个内角之和
D.内错角相等
6.(2020秋?宝应县期中)七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )
A.甲、乙、丙、丁
B.甲、丙、乙、丁
C.甲、丁、乙、丙
D.甲、丙、丁、乙
7.(2021春?工业园区期末)如图,若△ABC≌△ADE,则下列结论中不一定成立的是( )
A.∠ACB=∠DAC
B.AC=AE
C.BC=DE
D.∠BAD=∠CDE
8.(2021春?泰兴市期末)下列所给的四组条件中,能作出唯一三角形的是( )
A.AB=2cm,BC=6cm,AC=3cm
B.BC=3cm,AC=5cm,∠B=90°
C.∠A=∠B=∠C=60°
D.AB=4cm,AC=6cm,∠C=30°
9.(2021春?泰兴市期末)如图所示,AP平分∠BAC,点M,N分别在边AB,AC上,如果添加一个条件,即可推出AM=AN,那么下面条件不正确的是( )
A.PM=PN
B.∠APM=∠APN
C.MN⊥AP
D.∠AMP=∠ANP
10.(2021?淮安)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2
B.4
C.6
D.8
11.(2021春?洪江市期末)如图,在△ABC中,∠B=90°,AD平分∠BAC,BC=10,CD=6,则点D到AC的距离为( )
A.4
B.6
C.8
D.10
12.(2019秋?扎鲁特旗期末)如图,用尺规作一个角等于已知角,其理论依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
二.填空题(每小题4分,共24分)
13.(2021?淮安)一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是
.
14.(2021?常州)如图,在△ABC中,点D、E分别在BC、AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED=
°.
15.(2020?泰州)如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为
.
16.(2021春?南京期中)命题“垂直于同一条直线的两条直线平行”写成“如果…,那么…”的形式为:如果
,那么
.
17.(2021?东城区二模)如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是
.
18.(2020秋?江都区期末)如图,点A,B,C在同一条直线上,∠A=∠DBE=∠C=90°,请你只添加一个条件,使得△DAB≌△BCE.你添加的条件是
.(要求:不再添加辅助线,只需填一个答案即可)
三.解答题(共60分)
19.(6分)(2017春?辉县市期末)如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
20.(6分)(2020春?相城区期中)若a,b,c是△ABC三边的长,化简:|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a﹣b|.
21.(10分)(2020秋?前郭县期末)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.
(1)若∠BAC=70°,求:∠BOC的度数;
(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)
22.(10分)(2021春?吴中区月考)如图,在△ABC中,DE是AC的垂直平分线.
(1)若AC=6,△ABD的周长是13,则△ABC的周长是
;
(2)若△ABC中,∠B=62°,∠C=36°,求∠BAD的度数.
23.(10分)(2019秋?亭湖区校级期中)已知:如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,垂足分别为E、F.
(1)求证:PE=PF;
(2)若∠BAC=60°,连接AP,求∠EAP的度数.
24.(8分)(2021?涟水县模拟)如图,点A、F、C、D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:△ABC≌△DEF.
25.(10分)(2020秋?宝应县期末)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
(1)求证:BC=DC;
(2)若∠A=25°,∠D=15°,求∠ACB的度数.
2021-2022浙教版数学八上第一章三角形的初步认识常考必刷题
参考答案与试题解析
一.选择题
1.(2021春?靖江市期末)下列各组图形中,表示AD是△ABC中BC边的高的图形为( )
A.
B.
C.
D.
【分析】根据高的定义:”过三角形的顶点向对边作垂线,顶点和垂足之间的线段叫做三角形的高线“解答.
【解答】解:△ABC的高AD是过顶点A与BC垂直的线段,只有D选项符合.
故选:D.
2.(2021春?金坛区期末)若一个三角形的两边长分别是3cm,6cm,则它的第三边的长可以是( )
A.3cm
B.6cm
C.9cm
D.12cm
【分析】首先设第三边长为xcm,根据三角形的三边关系可得6﹣3<x<6+3,再解不等式即可.
【解答】解:设第三边长为xcm,根据三角形的三边关系可得:
6﹣3<x<6+3,
解得:3<x<9,
故选:B.
3.(2021春?崇川区校级月考)如图,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( )
A.50°
B.60°
C.30°
D.40°
【分析】先根据∠1=50°由平行线的性质求出∠A的度数,根据直角三角形两锐角互余的性质即可求出∠B的度数.
【解答】解:∵EF∥AB,
∴∠A=∠1=50°,
∵△ABC是直角三角形,
∴∠B=90°﹣∠A=90°﹣50°=40°.
故选:D.
4.(2021?盐城)将一副三角板按如图方式重叠,则∠1的度数为( )
A.45°
B.60°
C.75°
D.105°
【分析】直接利用一副三角板的内角度数,再结合三角形外角的性质得出答案.
【解答】解:根据三角板的度数知,∠ABC=∠ACB=45°,∠DBC=30°,
∴∠1=∠DBC+∠ACB=30°+45°=75°,
故选:C.
5.(2021春?广陵区校级期中)下列命题中是真命题的是( )
A.相等的角是对顶角
B.如果a3=b3,那么a=b
C.三角形的一个外角等于两个内角之和
D.内错角相等
【分析】根据对顶角的定义、等式的性质、三角形的角及平行线的性质判断即可.
【解答】解:A、相等的角不一定是对顶角,原命题是假命题;
B、如果a3=b3,那么a=b,是真命题;
C、三角形的一个外角等于与它不相邻的两个内角之和,原命题是假命题;
D、两直线平行,内错角相等,原命题是假命题;
故选:B.
6.(2020秋?宝应县期中)七年级(1)班的四位同学参加数学知识竞赛活动,分别获得第一、二、三、四名,大家猜测谁得第几名时,明明说:“甲得第一,乙得第二”;文文说:“甲得第二,丁得第四”;凡凡说:“丙得第二,丁得第三”.名次公布后,他们每人只猜对一半,那么甲、乙、丙、丁的名次顺序为( )
A.甲、乙、丙、丁
B.甲、丙、乙、丁
C.甲、丁、乙、丙
D.甲、丙、丁、乙
【分析】因为他们每人只猜对一半,可以先假设明明说“甲得第一”是正确的,由此推导:分别分析得出所有的可能即可.
【解答】解:因为他们每人只猜对一半,
可以先假设明明说“甲得第一”是正确的,由此推导:
明明:甲得第一→文文:丁得第四→凡凡:丙得第二→乙得第三,成立;
若假设明明说“乙得第二”是正确的,由此进行推导:
明明:乙得第二→文文:丁得第四→凡凡:丙得第二,矛盾.
所以甲、乙、丙、丁的名次顺序为甲、丙、乙、丁.
故选:B.
7.(2021春?工业园区期末)如图,若△ABC≌△ADE,则下列结论中不一定成立的是( )
A.∠ACB=∠DAC
B.AC=AE
C.BC=DE
D.∠BAD=∠CDE
【分析】根据翻三角形全等的性质一一判断即可.
【解答】解:∵△ABC≌△ADE,
∴AD=AB,AE=AC,BC=DE,∠ABC=∠ADE,
∴∠BAD=∠CAE,
∵AD=AB,
∴∠ABD=∠ADB,
∴∠BAD=180°﹣∠ABD﹣∠ADB,
∴∠CDE=180°﹣∠ADB﹣ADE,
∵∠ABD=∠ADE,
∴∠BAD=∠CDE
故B、C、D选项不符合题意,
故选:A.
8.(2021春?泰兴市期末)下列所给的四组条件中,能作出唯一三角形的是( )
A.AB=2cm,BC=6cm,AC=3cm
B.BC=3cm,AC=5cm,∠B=90°
C.∠A=∠B=∠C=60°
D.AB=4cm,AC=6cm,∠C=30°
【分析】根据三角形三边的关系对A进行判断;根据全等三角形的判定方法对B、C、D进行判断.
【解答】解:A、因为AB+AC<BC,三条线段不能组成三角形,所以A选项不符合题意;
B、BC=3cm,AC=5cm,∠B=90°,根据“HL”可判断此三角形为唯一三角形,所以B选项符合题意;
C、利用∠A=∠B=∠C=60°不能确定三角形的大小,所以C选项不符合题意;
D、利用AB=4cm,AC=6cm,∠C=30°可画出两三角形,所以D选项不符合题意.
故选:B.
9.(2021春?泰兴市期末)如图所示,AP平分∠BAC,点M,N分别在边AB,AC上,如果添加一个条件,即可推出AM=AN,那么下面条件不正确的是( )
A.PM=PN
B.∠APM=∠APN
C.MN⊥AP
D.∠AMP=∠ANP
【分析】根据已知条件结合三角形全等的判定方法,验证各选项提供的条件是否能证△APM≌△APN即可.
【解答】解:∵AP平分∠BAC,∴∠BAP=∠CAP,
A、由∠BAP=∠CAP,PM=PN,AP=AP,不能判定△APM≌△APN,
∴不推出AM=AN,故选项A符合题意;
B、由∠BAP=∠CAP,AP=AP,∠APM=∠APN,能判定△APM≌△APN(ASA),
∴AM=AN,故选项B不符合题意;
C、∵MN⊥AP,
∴∠APM=∠APN=90°,
又由∠BAP=∠CAP,AP=AP,能判定△APM≌△APN(ASA),
∴AM=AN,故选项C不符合题意;
D、由∠BAP=∠CAP,AP=AP,∠AMP=∠ANP,能判定△APM≌△APN(AAS),
∴AM=AN,故选项D不符合题意;
故选:A.
10.(2021?淮安)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2
B.4
C.6
D.8
【分析】根据线段的垂直平分线的性质得到EB=EA=4,结合图形计算,得到答案.
【解答】解:∵DE是AB的垂直平分线,AE=4,
∴EB=EA=4,
∴BC=EB+EC=4+2=6,
故选:C.
11.(2021春?洪江市期末)如图,在△ABC中,∠B=90°,AD平分∠BAC,BC=10,CD=6,则点D到AC的距离为( )
A.4
B.6
C.8
D.10
【分析】由条件可先求得BD的长,再根据角平分线的性质可知D到AC的距离等于BD,可得到答案.
【解答】解:∵BC=10,CD=6,
∴BD=BC﹣CD=10﹣6=4,
△ABC中,∠B=90°,AD平分∠BAC,
∴点D到AC的距离=BD=4.
故选:A.
12.(2019秋?扎鲁特旗期末)如图,用尺规作一个角等于已知角,其理论依据是( )
A.SSS
B.SAS
C.ASA
D.AAS
【分析】根据作图过程以及全等三角形的判定方法进行判断解答.
【解答】解:根据作图过程可知,
OC=O′C′,OD=O′D′,CD=C′D′,
∴利用的是三边对应相等,两三角形全等,
即作图原理是SSS.
故选:A.
二.填空题
13.(2021?淮安)一个三角形的两边长分别是1和4,若第三边的长为偶数,则第三边的长是
4 .
【分析】利用三角形三边关系定理,先确定第三边的范围,再根据第三边是偶数这一条件,求得第三边的值.
【解答】解:设第三边为a,根据三角形的三边关系知,
4﹣1<a<4+1,即3<a<5,
又∵第三边的长是偶数,
∴a为4.
故答案为:4.
14.(2021?常州)如图,在△ABC中,点D、E分别在BC、AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED= 100 °.
【分析】利用平行线的性质以及三角形的内角和定理解决问题即可.
【解答】解:在△ABC中,∠BAC+∠B+∠C=180°,
∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵DE∥AB,
∴∠A+∠AED=180°,
∴∠AED=180°﹣80°=100°.
故答案为:100.
15.(2020?泰州)如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为 140° .
【分析】根据三角形外角性质求出求出∠DFB,再根据三角形外角性质求出∠α即可.
【解答】解:如图,
∵∠B=30°,∠DCB=65°,
∴∠DFB=∠B+∠DCB=30°+65°=95°,
∴∠α=∠D+∠DFB=45°+95°=140°,
故答案为:140°.
16.(2021春?南京期中)命题“垂直于同一条直线的两条直线平行”写成“如果…,那么…”的形式为:如果 两条直线垂直于同一条直线 ,那么 这两条直线互相平行 .
【分析】把命题的题设部分写在如果的后面,把结论部分写在那么的后面.
【解答】解:命题“垂直于同一条直线的两条直线平行”改写成“如果…,那么…”的形式为:如果两条直线垂直于同一条直线,那么这两条直线互相平行,
故答案为:两条直线垂直于同一条直线,那么这两条直线相互平行.
17.(2021?东城区二模)如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是 BC=DF(答案不唯一) .
【分析】根据全等三角形的判定方法可以由SSS证明△ABC≌△EDF.
【解答】解:添加BC=DF.
∵AD=BE,
∴AD+DB=BE+BD,
∴AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS),
故答案为:BC=DF(答案不唯一).
18.(2020秋?江都区期末)如图,点A,B,C在同一条直线上,∠A=∠DBE=∠C=90°,请你只添加一个条件,使得△DAB≌△BCE.你添加的条件是 DB=BE(答案不唯一) .(要求:不再添加辅助线,只需填一个答案即可)
【分析】此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.
【解答】解:添加的条件是DB=BE,
理由是:∵∠A=∠DBE=90°,
∴∠D+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠D=∠CBE,
在△DAB和△BCE中,
,
∴△DAB≌△BCE(AAS),
故答案为:DB=BE(答案不唯一).
三.解答题
19.(2017春?辉县市期末)如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
【分析】根据直角三角形两锐角互余求出∠AED,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE,然后根据角平分线的定义求出∠BAC,再利用三角形的内角和定理列式计算即可得解.
【解答】解:∵AD是BC边上的高,∠EAD=5°,
∴∠AED=85°,
∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
20.(2020春?相城区期中)若a,b,c是△ABC三边的长,化简:|a+b﹣c|+|b﹣a﹣c|﹣|c﹣a﹣b|.
【分析】根据三角形的三边关系判断出a+b﹣c,b﹣a﹣c及c﹣a﹣b的符号,再去绝对值符号,合并同类项即可.
【解答】解:∵a、b、c是△ABC的三边的长,
∴a+b﹣c>0,b﹣a﹣c<0,c﹣a﹣b<0,
∴原式=a+b﹣c﹣b+a+c+c﹣a﹣b=a﹣b+c.
21.(2020秋?前郭县期末)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.
(1)若∠BAC=70°,求:∠BOC的度数;
(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)
【分析】(1)根据三角形的角平分线定义和三角形的内角和定理求出∠OBC+∠OCB的度数,再根据三角形的内角和定理即可求出∠BOC的度数;
(2)根据三角形外角平分线的性质可得∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB);根据三角形内角和定理可得∠BDC=90°﹣∠A.
【解答】解:(1)∵OB、OC分别是∠ABC和∠ACB的角平分线,
∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB),
∵∠A=70°,
∴∠OBC+∠OCB=(180°﹣70°)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)
=180°﹣55°
=125°;
(2)∠BDC=90°﹣∠A.
理由如下:
∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,
∴∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB),
由三角形内角和定理得,∠BDC=180°﹣∠BCD﹣∠DBC,
=180°﹣[∠A+(∠A+∠ABC+∠ACB)],
=180°﹣(∠A+180°),
=90°﹣∠A;
22.(2021春?吴中区月考)如图,在△ABC中,DE是AC的垂直平分线.
(1)若AC=6,△ABD的周长是13,则△ABC的周长是 19 ;
(2)若△ABC中,∠B=62°,∠C=36°,求∠BAD的度数.
【分析】(1)根据线段垂直平分线的性质得到DA=DC,根据三角形的周长公式计算,得到答案;
(2)根据三角形内角和定理求出∠BAC,根据等腰三角形的性质求出∠DAC,计算即可.
【解答】解:(1)∵DE是AC的垂直平分线,
∴DA=DC,
∵△ABD的周长是13,
∴AB+AD+BD=AB+DC+BD=AB+BC=13,
∴△ABC的周长=AB+BC+AC=13+6=19,
故答案为:19;
(2)在△ABC中,∠B=62°,∠C=36°,
则∠BAC=180°﹣∠B﹣∠C=82°,
∵DA=DC,
∴∠DAC=∠C=36°,
∴∠BAD=∠BAC﹣∠DAC=82°﹣36°=46°.
23.(2019秋?亭湖区校级期中)已知:如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,垂足分别为E、F.
(1)求证:PE=PF;
(2)若∠BAC=60°,连接AP,求∠EAP的度数.
【分析】(1)过点P作PD⊥BC于D,可得PD=PE=PF;
(2)可得AP是∠BAC的平分线,则∠EAP可求出.
【解答】解:(1)过点P作PD⊥BC于D,
∵∠ABC和∠ACB的角平分线相交于点P,且PE⊥AB,PF⊥AC,
∴PD=PE,PD=PF,
∴PE=PF;
(2)∵PE=PF,PE⊥AB,PF⊥AC,
∴AP平分∠BAC,
∵∠BAC=60°,
∴∠EAP==30°.
24.(2021?涟水县模拟)如图,点A、F、C、D在同一条直线上,AB∥DE,AB=DE,AF=DC.求证:△ABC≌△DEF.
【分析】根据平行线的性质得出∠A=∠D,求出AC=DF,再根据全等三角形的判定定理推出即可.
【解答】证明:∵AB∥DE,
∴∠A=∠D,
∵AF=DC,
∴AF+CF=DC+CF,
即AC=DF,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS).
25.(2020秋?宝应县期末)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E.
(1)求证:BC=DC;
(2)若∠A=25°,∠D=15°,求∠ACB的度数.
【分析】(1)根据ASA证明△BCA≌△DCE,进而利用全等三角形的性质解答即可;
(2)根据全等三角形的性质解答即可.
【解答】证明:(1)∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ECA,
即∠BCA=∠DCE,
在△BCA和△DCE中,
,
∴△BCA≌△DCE(ASA),
∴BC=DC;
(2)∵△BCA≌△DCE,
∴∠B=∠D=15°,
∵∠A=25°,
∴∠ACB=180°﹣∠A﹣∠B=140°.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
