浙教版八年级上册第一章 三角形的初步认识培优训练卷(含答案)
文档属性
| 名称 | 浙教版八年级上册第一章 三角形的初步认识培优训练卷(含答案) | 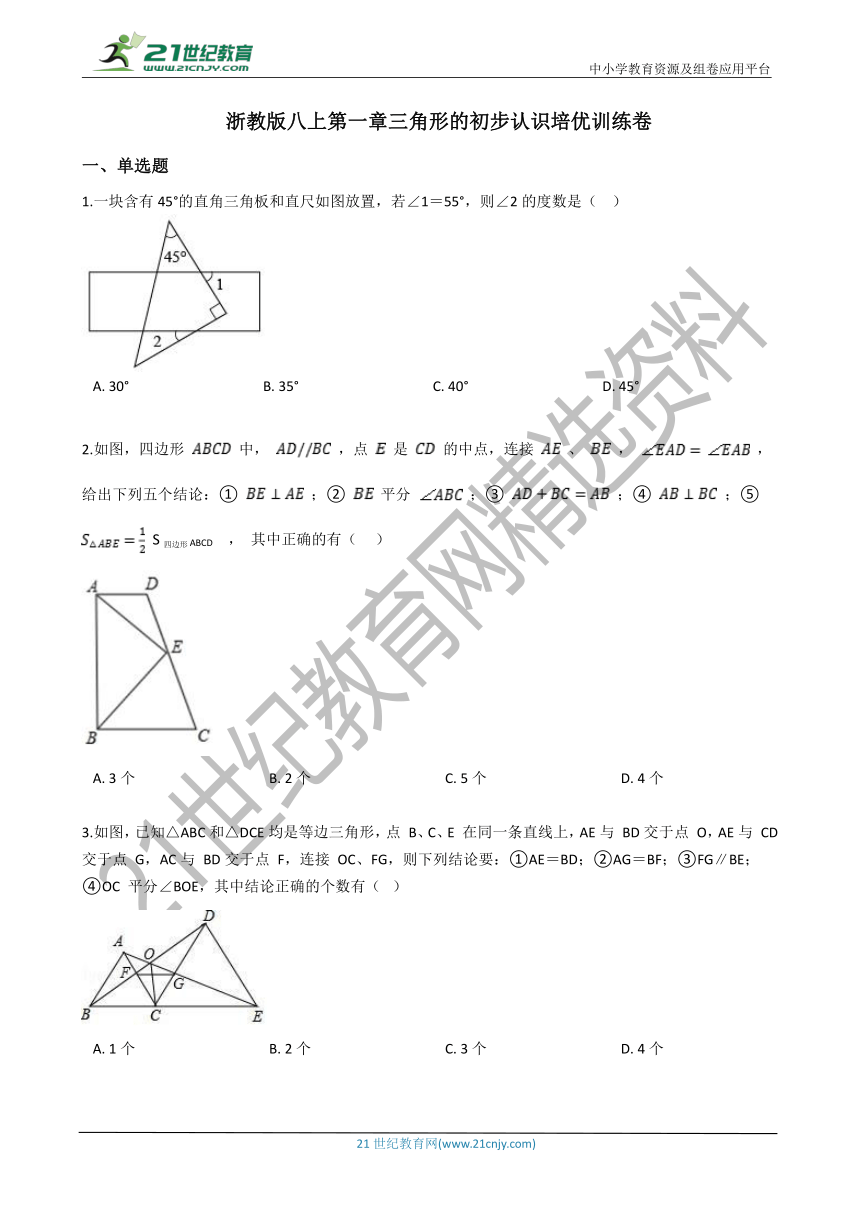 | |
| 格式 | zip | ||
| 文件大小 | 389.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-17 16:01:25 | ||
图片预览





文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
浙教版八上第一章三角形的初步认识培优训练卷
一、单选题
1.一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是(??
)
A.?30°???????????????????????????????????????B.?35°???????????????????????????????????????C.?40°???????????????????????????????????????D.?45°
2.如图,四边形
中,
,点
是
的中点,连接
、
,
,给出下列五个结论:①
;②
平分
;③
;④
;⑤
S四边形ABCD
,
其中正确的有(???
)
A.?3个???????????????????????????????????????B.?2个???????????????????????????????????????C.?5个???????????????????????????????????????D.?4个
3.如图,已知△ABC和△DCE均是等边三角形,点
B、C、E
在同一条直线上,AE与
BD交于点
O,AE与
CD交于点
G,AC与
BD交于点
F,连接
OC、FG,则下列结论要:①AE=BD;②AG=BF;③FG∥BE;④OC
平分∠BOE,其中结论正确的个数有(?
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.已知△ABC的两条中线的长分别为5、10,若第三条中线的长也是整数,则第三条中线长的最大值(??
)
A.?7??????????????????????????????????????????B.?8??????????????????????????????????????????C.?14??????????????????????????????????????????D.?15
5.如图,Rt△ABC中,AC=BC=2,点D,E分别是AB,AC的中点,在CD上找一点P,使PA+PE最小,则这个最小值是(???
)
A.?4???????????????????????????????????????B.????????????????????????????????????????C.?
+1???????????????????????????????????????D.?
6.如图,在△ABC中,E
,
D分别是边AB
,
AC上的点,且AE=AD
,
BD
,
CE交于点F
,
AF的延长线交BC于点H
,
若∠EAF=∠DAF
,
则图中的全等三角形共有(???
)
A.?4对???????????????????????????????????????B.?5对???????????????????????????????????????C.?6对???????????????????????????????????????D.?7对
7..如图,在
中,
,按以下步骤作图:
①以点
为圆心,以小于
的长为半径画弧,分别交
、
于点
、
;
②分别以点
、
为圆心,以大于
的长为半径画弧,两弧相交于点
;
③作射线
,交
边于点
,
若
,
,则
(??
)
A.?3?????????????????????????????????????????B.??????????????????????????????????????????C.?6?????????????????????????????????????????D.?
8.如图,
是
的中线,
,
分别是
和
延长线上的点,连接
,
,且
.
.有下列说法:①
;②
和
的面积相等;③
;④
.其中正确的有(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
9.已知△ABC
,
(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A.上述说法正确的个数是(???
)
?
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
10.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP=MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有(?
?)
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
二、填空题
11.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S
=
现已知△ABC的三边长分别为1,2,
,则△ABC的面积为________
12.如图,在△ABC中,AB=AC=24厘米,∠B=∠C
,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为________厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
13.如图,
分别是
的边
上的中点,连接
交于点G,
,
的面积为6,设
的面积为
,
的面积为
,则
________.
14.如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=2,AB=9,则CF=________.
?
??
15.等腰三角形一腰上的高线与另一腰夹角为40°,则该三角形的顶角为________。
16.如图,
,点
是边
上的点,
平分
,
平分
,有下列结论:①
,②
为
的中点,③
,④
,其中正确的有________.(填序号)
三、解答题
17.如图:△ABC中,AC>AB.
(1)作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ.(尺规作图,保留作图痕迹,不需要写作法)
(2)在(1)的条件下,若BC=14,求△APQ的周长.
18.如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=2,CF=4时,求AC的长.
19.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC、BC于点M、N.
(1)如图①,若∠BAC=110°,求∠EAN的度数;
(2)如图②,若∠BAC=80°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出∠EAN的大小(用含α的代数式表示).
20.如图,四边形ABCD中,AD∥BC
,
AD=BC
,
连接BD
,
点E、F在BD上,点G、H分别在边AD、BC上,连接EG、FH
,
且BE=DF
,
EG∥FH
,
连接GH交BD于点O
.
(1)求证:EG=FH;
(2)在不添加辅助线的情况下,写出图中所有的全等三角形.
21.如图,在△ABC
中,AB=7,BC=14,M为AC的中点,OM⊥AC
交
的平分线于O,OE⊥AB交BA的延长线于E,OF⊥BC.垂足为F.
(1)求证:AE=CF.
(2)求线段BE的长.
22.??
(1)如图①,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图②,已知AF平分∠BAC,交边BC于点E,延长AE至点F,过点F作FD⊥BC于点D,若∠B=x°,∠C=(x+36)°.
①∠CAE=?
▲?
(含x的代数式表示);
②求∠F的度数.
23.??
(1)如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是?
▲?
;
②∠APD的度数为?
▲?
.
(2)(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出符合题意结论再给予证明;
(3)(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为________.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
D
3.【答案】
D
4.【答案】
C
5.【答案】
B
6.【答案】
C
7.【答案】
B
8.【答案】
C
9.【答案】
C
10.【答案】
D
二、填空题
11.【答案】
1
12.【答案】
4或6
13.【答案】
2
14.【答案】
5
15.【答案】
50°或130°
16.【答案】
②③④
三、解答题
17.【答案】
(1)解:作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ
.
(2)解:∵AB边的垂直平分线交BC于点P,AC边的垂直平分线交BC于点Q,
∴AP=BP,AQ=CQ;
∵△APQ的周长为AP+PQ+QA=BP+PQ+CQ=BC=14.
18.【答案】
(1)证明:∵CF∥AB.∴∠B=∠FCD,∠BED=∠F,
∵AD是BC边上的中线,∴BD=CD,
在△BDE和△CDF中,
∴△BDE≌△CDF(
AAS)
(2)解:∵△BDE≌△CDF,
∴BE=CF=4,∴AB=AE+BE=2+4=6,
∵AD⊥BC,BD=CD.∴AD垂直平分BC,∴AC=AB=
6.
19.【答案】
(1)解:∵DE垂直平分AB,
∴AE=BE,∴∠BAE=∠B,
同理可得,C
CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),
在△ABC中,C
B+∠C=
180°-∠BAC=
180°-110°=
70°,
∴∠EAN=
110°-70°
=
40°.
(2)解:∵DE垂直平分AB,
∴AE=BE,∴∠BAE=∠B,
同理可得,∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=
180°-∠BAC=
180°-80°
=
100°,
∴∠EAN=
100°-80°=
20°.
(3)解:当0°<α<90°时,∠EAN=
180°-2α;
当90°2α-
180°.
20.【答案】
(1)证明:∵AD∥BC,
∴∠GDE=∠HBF,
∵EG∥FH,
∴∠GED=∠HFB,
∵BE=DF,
∴BD﹣BE=BD﹣DF,
即:DE=BF,
在△GED和△HFB中,
,
∴△GED≌△HFB(ASA),
∴EG=FH
(2)解:由(1)得:△GED≌△HFB,
∵EG∥FH,
∴∠OEG=∠OFH,∠OGF=∠OHF,
在△OEG和△OFH中,
,
∴△OEG≌△OFH(ASA),
∴OG=OH,
∵AD∥BC,
∴∠OGD=∠OHB,∠ADB=∠CBD,
在△OGD和△OHB中,
,
∴△OGD≌△OHB(ASA),
在△ADB和△CBD中,
,
∴△ADB≌△CBD(SAS),
∴在不添加辅助线的情况下,图中所有的全等三角形为:△GED≌△HFB,△OEG≌△OFH,△OGD≌△OHB,△ADB≌△CBD
21.【答案】
(1)解:连接OA
∵OB平分
,
又∵OE⊥AB,OF⊥BC,
∴OE=OF.
∵OM⊥AC,M为AC中点,
∴OM垂直平分AC,
∴OA=OC,
∴△AEO≌△CFO(HL),
∴AE=CF.
(2)解:∵OB平分
∴
又∵OE⊥AB,OF⊥BC
∴
又OB=OB
∴△BEO≌△BFO(AAS),
∴BE=BF.
∵AB=7,BC=14,
设AE=CF=x,
∴x+7=14-x,
,
∴BE=7+
.
22.【答案】
(1)解:∵∠B=30°,∠C=50°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-30°-50°=100°.
∵AE是△ABC的角平分线,即AE平分∠BAC,
∴
.
∵AD是△ABC的高,即AD⊥BC,
∴在Rt△ADC中,∠CAD=90°-∠C=90°-50°=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2)解:①∵∠B=x°,∠C=(x+36)°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-x°-(x+36)°=(144-2x)°.
∵AF平分∠BAC,
∴
.
故本小题应填写:
.
②∵AF平分∠BAC,
∴∠BAE=∠CAE=72°-x°.
∵∠AEC是△ABE的一个外角,
∴∠AEC=∠BAE+∠B=72°-x°+x°=72°,
∴∠FED=∠AEC=72°.
∵FD⊥BC,
∴在Rt△EDF中,∠F=90°-∠FED=90°-72°=18°.
23.【答案】
(1)解:结论:AE=BD.∠APD=60°.
理由:设AE交CD于点O.
∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAO=∠ODP,
∵∠AOC=∠DOP,
∴∠DPO=∠ACO=60°,
即∠APD=60°.
故答案为AE=BD,60°.
(2)结论仍然成立.
理由:设AC交BD于点O.
∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB
∴△ACE≌△DCB(SAS),
∴AE=BD,∠PAO=∠ODC,
∵∠AOP=∠DOC,
∴∠APO=∠DCO=60°,
即∠APD=60°.
(3)50
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
浙教版八上第一章三角形的初步认识培优训练卷
一、单选题
1.一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是(??
)
A.?30°???????????????????????????????????????B.?35°???????????????????????????????????????C.?40°???????????????????????????????????????D.?45°
2.如图,四边形
中,
,点
是
的中点,连接
、
,
,给出下列五个结论:①
;②
平分
;③
;④
;⑤
S四边形ABCD
,
其中正确的有(???
)
A.?3个???????????????????????????????????????B.?2个???????????????????????????????????????C.?5个???????????????????????????????????????D.?4个
3.如图,已知△ABC和△DCE均是等边三角形,点
B、C、E
在同一条直线上,AE与
BD交于点
O,AE与
CD交于点
G,AC与
BD交于点
F,连接
OC、FG,则下列结论要:①AE=BD;②AG=BF;③FG∥BE;④OC
平分∠BOE,其中结论正确的个数有(?
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.已知△ABC的两条中线的长分别为5、10,若第三条中线的长也是整数,则第三条中线长的最大值(??
)
A.?7??????????????????????????????????????????B.?8??????????????????????????????????????????C.?14??????????????????????????????????????????D.?15
5.如图,Rt△ABC中,AC=BC=2,点D,E分别是AB,AC的中点,在CD上找一点P,使PA+PE最小,则这个最小值是(???
)
A.?4???????????????????????????????????????B.????????????????????????????????????????C.?
+1???????????????????????????????????????D.?
6.如图,在△ABC中,E
,
D分别是边AB
,
AC上的点,且AE=AD
,
BD
,
CE交于点F
,
AF的延长线交BC于点H
,
若∠EAF=∠DAF
,
则图中的全等三角形共有(???
)
A.?4对???????????????????????????????????????B.?5对???????????????????????????????????????C.?6对???????????????????????????????????????D.?7对
7..如图,在
中,
,按以下步骤作图:
①以点
为圆心,以小于
的长为半径画弧,分别交
、
于点
、
;
②分别以点
、
为圆心,以大于
的长为半径画弧,两弧相交于点
;
③作射线
,交
边于点
,
若
,
,则
(??
)
A.?3?????????????????????????????????????????B.??????????????????????????????????????????C.?6?????????????????????????????????????????D.?
8.如图,
是
的中线,
,
分别是
和
延长线上的点,连接
,
,且
.
.有下列说法:①
;②
和
的面积相等;③
;④
.其中正确的有(???
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
9.已知△ABC
,
(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A.上述说法正确的个数是(???
)
?
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
10.如图,在△ABC中,BD、CE分别是∠ABC和∠ACB的平分线,AM⊥CE于P,交BC于M,AN⊥BD于Q,交BC于N,∠BAC=110°,AB=6,AC=5,MN=2,结论①AP=MP;②BC=9;③∠MAN=35°;④AM=AN.其中不正确的有(?
?)
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
二、填空题
11.我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,则该三角形的面积为S
=
现已知△ABC的三边长分别为1,2,
,则△ABC的面积为________
12.如图,在△ABC中,AB=AC=24厘米,∠B=∠C
,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为________厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
13.如图,
分别是
的边
上的中点,连接
交于点G,
,
的面积为6,设
的面积为
,
的面积为
,则
________.
14.如图,在△ABC中,点D为BC的中点,△AEF的边EF过点C,且AE=EF,AB∥EF,AD平分∠BAE,CE=2,AB=9,则CF=________.
?
??
15.等腰三角形一腰上的高线与另一腰夹角为40°,则该三角形的顶角为________。
16.如图,
,点
是边
上的点,
平分
,
平分
,有下列结论:①
,②
为
的中点,③
,④
,其中正确的有________.(填序号)
三、解答题
17.如图:△ABC中,AC>AB.
(1)作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ.(尺规作图,保留作图痕迹,不需要写作法)
(2)在(1)的条件下,若BC=14,求△APQ的周长.
18.如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF;
(2)当AD⊥BC,AE=2,CF=4时,求AC的长.
19.在△ABC中,DE垂直平分AB,分别交AB、BC于点D、E,MN垂直平分AC,分别交AC、BC于点M、N.
(1)如图①,若∠BAC=110°,求∠EAN的度数;
(2)如图②,若∠BAC=80°,求∠EAN的度数;
(3)若∠BAC=α(α≠90°),直接写出∠EAN的大小(用含α的代数式表示).
20.如图,四边形ABCD中,AD∥BC
,
AD=BC
,
连接BD
,
点E、F在BD上,点G、H分别在边AD、BC上,连接EG、FH
,
且BE=DF
,
EG∥FH
,
连接GH交BD于点O
.
(1)求证:EG=FH;
(2)在不添加辅助线的情况下,写出图中所有的全等三角形.
21.如图,在△ABC
中,AB=7,BC=14,M为AC的中点,OM⊥AC
交
的平分线于O,OE⊥AB交BA的延长线于E,OF⊥BC.垂足为F.
(1)求证:AE=CF.
(2)求线段BE的长.
22.??
(1)如图①,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图②,已知AF平分∠BAC,交边BC于点E,延长AE至点F,过点F作FD⊥BC于点D,若∠B=x°,∠C=(x+36)°.
①∠CAE=?
▲?
(含x的代数式表示);
②求∠F的度数.
23.??
(1)如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是?
▲?
;
②∠APD的度数为?
▲?
.
(2)(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出符合题意结论再给予证明;
(3)(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为________.
答案解析部分
一、单选题
1.【答案】
B
2.【答案】
D
3.【答案】
D
4.【答案】
C
5.【答案】
B
6.【答案】
C
7.【答案】
B
8.【答案】
C
9.【答案】
C
10.【答案】
D
二、填空题
11.【答案】
1
12.【答案】
4或6
13.【答案】
2
14.【答案】
5
15.【答案】
50°或130°
16.【答案】
②③④
三、解答题
17.【答案】
(1)解:作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ
.
(2)解:∵AB边的垂直平分线交BC于点P,AC边的垂直平分线交BC于点Q,
∴AP=BP,AQ=CQ;
∵△APQ的周长为AP+PQ+QA=BP+PQ+CQ=BC=14.
18.【答案】
(1)证明:∵CF∥AB.∴∠B=∠FCD,∠BED=∠F,
∵AD是BC边上的中线,∴BD=CD,
在△BDE和△CDF中,
∴△BDE≌△CDF(
AAS)
(2)解:∵△BDE≌△CDF,
∴BE=CF=4,∴AB=AE+BE=2+4=6,
∵AD⊥BC,BD=CD.∴AD垂直平分BC,∴AC=AB=
6.
19.【答案】
(1)解:∵DE垂直平分AB,
∴AE=BE,∴∠BAE=∠B,
同理可得,C
CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),
在△ABC中,C
B+∠C=
180°-∠BAC=
180°-110°=
70°,
∴∠EAN=
110°-70°
=
40°.
(2)解:∵DE垂直平分AB,
∴AE=BE,∴∠BAE=∠B,
同理可得,∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=
180°-∠BAC=
180°-80°
=
100°,
∴∠EAN=
100°-80°=
20°.
(3)解:当0°<α<90°时,∠EAN=
180°-2α;
当90°
180°.
20.【答案】
(1)证明:∵AD∥BC,
∴∠GDE=∠HBF,
∵EG∥FH,
∴∠GED=∠HFB,
∵BE=DF,
∴BD﹣BE=BD﹣DF,
即:DE=BF,
在△GED和△HFB中,
,
∴△GED≌△HFB(ASA),
∴EG=FH
(2)解:由(1)得:△GED≌△HFB,
∵EG∥FH,
∴∠OEG=∠OFH,∠OGF=∠OHF,
在△OEG和△OFH中,
,
∴△OEG≌△OFH(ASA),
∴OG=OH,
∵AD∥BC,
∴∠OGD=∠OHB,∠ADB=∠CBD,
在△OGD和△OHB中,
,
∴△OGD≌△OHB(ASA),
在△ADB和△CBD中,
,
∴△ADB≌△CBD(SAS),
∴在不添加辅助线的情况下,图中所有的全等三角形为:△GED≌△HFB,△OEG≌△OFH,△OGD≌△OHB,△ADB≌△CBD
21.【答案】
(1)解:连接OA
∵OB平分
,
又∵OE⊥AB,OF⊥BC,
∴OE=OF.
∵OM⊥AC,M为AC中点,
∴OM垂直平分AC,
∴OA=OC,
∴△AEO≌△CFO(HL),
∴AE=CF.
(2)解:∵OB平分
∴
又∵OE⊥AB,OF⊥BC
∴
又OB=OB
∴△BEO≌△BFO(AAS),
∴BE=BF.
∵AB=7,BC=14,
设AE=CF=x,
∴x+7=14-x,
,
∴BE=7+
.
22.【答案】
(1)解:∵∠B=30°,∠C=50°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-30°-50°=100°.
∵AE是△ABC的角平分线,即AE平分∠BAC,
∴
.
∵AD是△ABC的高,即AD⊥BC,
∴在Rt△ADC中,∠CAD=90°-∠C=90°-50°=40°,
∴∠DAE=∠CAE-∠CAD=50°-40°=10°.
(2)解:①∵∠B=x°,∠C=(x+36)°,
∴在△ABC中,∠BAC=180°-∠B-∠C=180°-x°-(x+36)°=(144-2x)°.
∵AF平分∠BAC,
∴
.
故本小题应填写:
.
②∵AF平分∠BAC,
∴∠BAE=∠CAE=72°-x°.
∵∠AEC是△ABE的一个外角,
∴∠AEC=∠BAE+∠B=72°-x°+x°=72°,
∴∠FED=∠AEC=72°.
∵FD⊥BC,
∴在Rt△EDF中,∠F=90°-∠FED=90°-72°=18°.
23.【答案】
(1)解:结论:AE=BD.∠APD=60°.
理由:设AE交CD于点O.
∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAO=∠ODP,
∵∠AOC=∠DOP,
∴∠DPO=∠ACO=60°,
即∠APD=60°.
故答案为AE=BD,60°.
(2)结论仍然成立.
理由:设AC交BD于点O.
∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB
∴△ACE≌△DCB(SAS),
∴AE=BD,∠PAO=∠ODC,
∵∠AOP=∠DOC,
∴∠APO=∠DCO=60°,
即∠APD=60°.
(3)50
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
