2021-2022学年浙教版八年级数学上册3.1 认识不等式 课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学上册3.1 认识不等式 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-21 07:14:27 | ||
图片预览




文档简介
(共15张PPT)
3.1
认识不等式
1.如图,是公路上对汽车的限速标志,表示汽车在该路段行驶的速度不得超过40km/h,用v
(km/h)表示汽车的速度,怎样表示v与40之间的关系?
请用适当的数学式子表示下列问题中的数量关系:
2.一辆汽车从A地开往B地,其平均速度为50km/h,用s表示两地的路程,t表示所需时间,怎样表示s与t之间的关系?
v≤40
S=50t
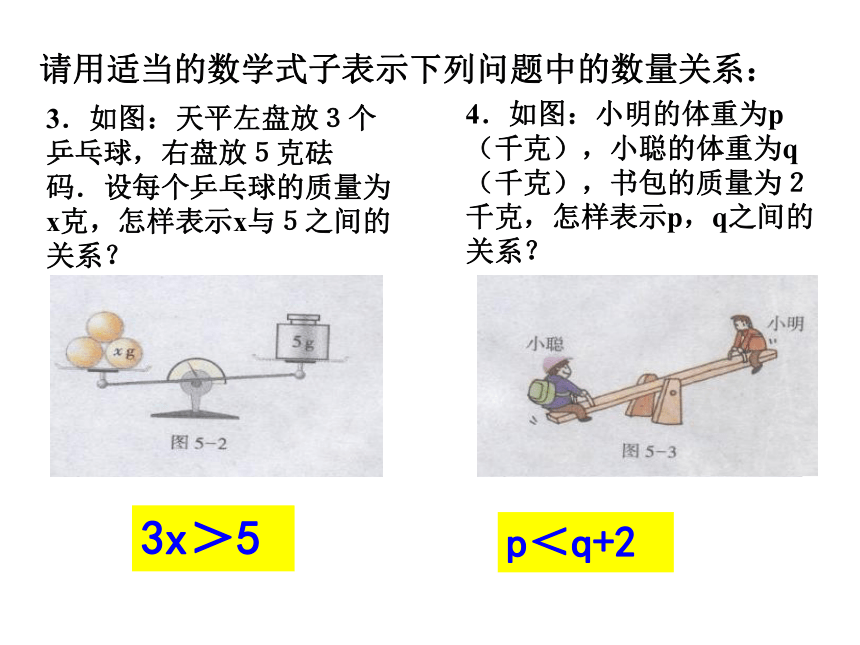
3.如图:天平左盘放3个乒乓球,右盘放5克砝码.设每个乒乓球的质量为x克,怎样表示x与5之间的关系?
4.如图:小明的体重为p(千克),小聪的体重为q(千克),书包的质量为2千克,怎样表示p,q之间的关系?
请用适当的数学式子表示下列问题中的数量关系:
3x>5
p<q+2
请用适当的数学式子表示下列问题中的数量关系:
5.某农户今年的收入比去年多1.5万元.记去年的收入为p万元,今年的收入为q万元,怎样表示p与q之间的关系?
q=p+1.5
6.经科学家测定,太阳表面的温度不低于6000℃,设太阳表面的温度为t
℃
,怎样表示t与6000之间的关系?
t≥6000
x≠3
7.要使代数式
有意义,x的值与3之间有什么关系?
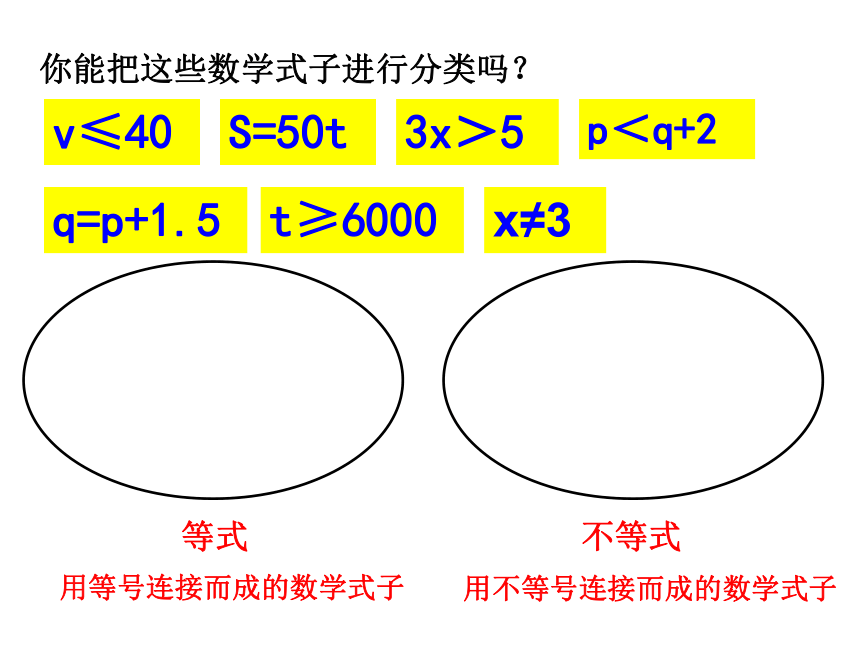
你能把这些数学式子进行分类吗?
v≤40
S=50t
p<q+2
q=p+1.5
t≥6000
x≠3
等式
不等式
用等号连接而成的数学式子
用不等号连接而成的数学式子
3x>5
判断下列各式中哪些是不等式?
(1)
a2+1>0
(2)
a+b=0
(3)
8<9
(4)
3x-1≤x
(5)
4-2x
(6)
x-y≠1
不等式的定义:
用符号“<”(或“≤”),“>”(或“≥”),“≠”连接而成的数学式子叫做不等式。
不等式也是刻画现实生活的重要模型。
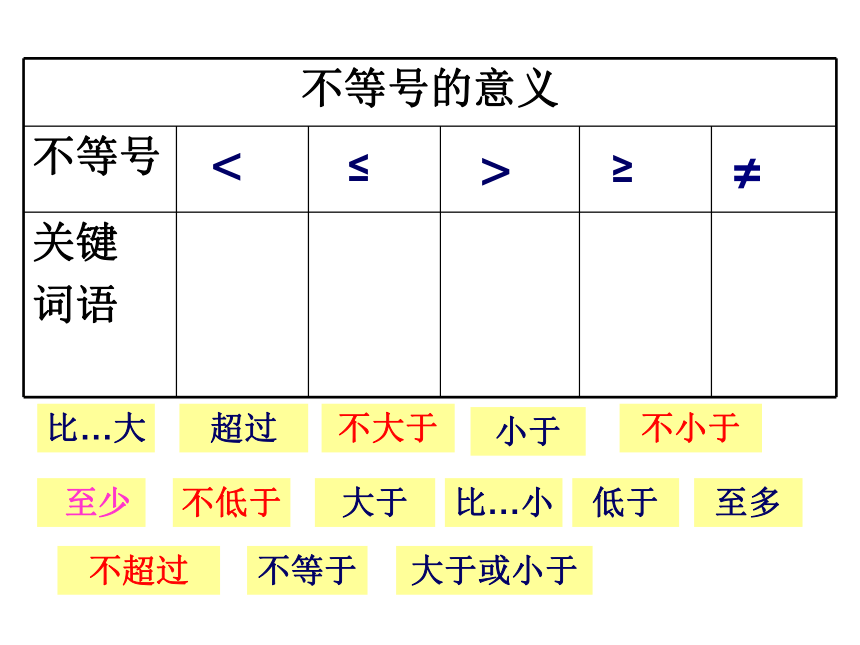
比…大
大于
小于
至多
不大于
不超过
不小于
不低于
至少
超过
低于
比…小
不等号的意义
不等号
关键
词语
>
<
≤
≥
≠
不等于
大于或小于
例1
根据下列数量关系列不等式:
(1)y的2倍与6的和比1小;
(2)x2减去10不大于10;
(3)a是正数。
(4)设a,b,c为一个三角形的三条边长,两边
之和大于第三边.
2y+6<1
x2-10≤10
a+b>c
a+c>b
b+c>a
小结:
找关键词,选不等号
a>0
0
1
-1
-2
-3
2
3
数轴
◆实数和数轴上的点一一对应。
◆数轴上表示的两个数,右边的数总比左边的数大。
◆三要素:原点;单位长度;正方向。
(1)
X>1
-5
-4
-3
-2
-1
0
1
2
3
4
5
(2)
X≤
-1.5
-5
-4
-3
-2
-1
0
1
2
3
4
5
在数轴上表示
不等式的步骤:
定界点
定方向
(3)
-1
≤
x
<
3
-5
-4
-3
-2
-1
0
1
2
3
4
5
把下列不等式表示在数轴上:
-1.5
练一练:说出下列各图所表示的关于x的不等式。
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
?
?
x<-2
x≥0
-3<x≤2
?
b
a
b≤x<a
例2
一座小水电站的水库水位在12~20m(包括12m,20m)时,发电机能正常工作。设水库水位为x(m).
(1)用不等式表示发电机正常工作水位范围,并表示在数轴上;
解:正常工作范围
12≤x≤20
0
2
4
6
8
10
12
14
16
18
20
22
x2
x1
x3
x4
显然,
x3,x4满足不等式12≤x≤20
,而x1,x2不满足,
当水位在15m,19m时,发电机能正常工作,
当水位在8m,10m时,发电机不能正常工作。
新知应用
(2)当水位在下列位置时,发电机能正常工作吗?
①x1=8;②x2=10;③x3=15;④x4=19.
用不等式和数轴给出解释。
16
点在范围内
数满足不等式
发电机能正常工作
在数轴上表示不等式
和
的下列取值:
,并利用数轴说明,
的这些取值中,哪些满足不等式
,哪些不满足.
巩固练习
一、数学知识:
不等式的概念:用符号“<”(或“≤”),“>”(或“≥”),“≠”连接而成的数学式子叫做不等式。
二、数学技能:
1.列不等式
2.用数轴表示不等式
三、数学思想:
1.
分类思想
2.
类比思想
3.
数形结合
谢谢大家的参与!
3.1
认识不等式
1.如图,是公路上对汽车的限速标志,表示汽车在该路段行驶的速度不得超过40km/h,用v
(km/h)表示汽车的速度,怎样表示v与40之间的关系?
请用适当的数学式子表示下列问题中的数量关系:
2.一辆汽车从A地开往B地,其平均速度为50km/h,用s表示两地的路程,t表示所需时间,怎样表示s与t之间的关系?
v≤40
S=50t
3.如图:天平左盘放3个乒乓球,右盘放5克砝码.设每个乒乓球的质量为x克,怎样表示x与5之间的关系?
4.如图:小明的体重为p(千克),小聪的体重为q(千克),书包的质量为2千克,怎样表示p,q之间的关系?
请用适当的数学式子表示下列问题中的数量关系:
3x>5
p<q+2
请用适当的数学式子表示下列问题中的数量关系:
5.某农户今年的收入比去年多1.5万元.记去年的收入为p万元,今年的收入为q万元,怎样表示p与q之间的关系?
q=p+1.5
6.经科学家测定,太阳表面的温度不低于6000℃,设太阳表面的温度为t
℃
,怎样表示t与6000之间的关系?
t≥6000
x≠3
7.要使代数式
有意义,x的值与3之间有什么关系?
你能把这些数学式子进行分类吗?
v≤40
S=50t
p<q+2
q=p+1.5
t≥6000
x≠3
等式
不等式
用等号连接而成的数学式子
用不等号连接而成的数学式子
3x>5
判断下列各式中哪些是不等式?
(1)
a2+1>0
(2)
a+b=0
(3)
8<9
(4)
3x-1≤x
(5)
4-2x
(6)
x-y≠1
不等式的定义:
用符号“<”(或“≤”),“>”(或“≥”),“≠”连接而成的数学式子叫做不等式。
不等式也是刻画现实生活的重要模型。
比…大
大于
小于
至多
不大于
不超过
不小于
不低于
至少
超过
低于
比…小
不等号的意义
不等号
关键
词语
>
<
≤
≥
≠
不等于
大于或小于
例1
根据下列数量关系列不等式:
(1)y的2倍与6的和比1小;
(2)x2减去10不大于10;
(3)a是正数。
(4)设a,b,c为一个三角形的三条边长,两边
之和大于第三边.
2y+6<1
x2-10≤10
a+b>c
a+c>b
b+c>a
小结:
找关键词,选不等号
a>0
0
1
-1
-2
-3
2
3
数轴
◆实数和数轴上的点一一对应。
◆数轴上表示的两个数,右边的数总比左边的数大。
◆三要素:原点;单位长度;正方向。
(1)
X>1
-5
-4
-3
-2
-1
0
1
2
3
4
5
(2)
X≤
-1.5
-5
-4
-3
-2
-1
0
1
2
3
4
5
在数轴上表示
不等式的步骤:
定界点
定方向
(3)
-1
≤
x
<
3
-5
-4
-3
-2
-1
0
1
2
3
4
5
把下列不等式表示在数轴上:
-1.5
练一练:说出下列各图所表示的关于x的不等式。
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5
-4
-3
-2
-1
0
1
2
3
4
5
?
?
x<-2
x≥0
-3<x≤2
?
b
a
b≤x<a
例2
一座小水电站的水库水位在12~20m(包括12m,20m)时,发电机能正常工作。设水库水位为x(m).
(1)用不等式表示发电机正常工作水位范围,并表示在数轴上;
解:正常工作范围
12≤x≤20
0
2
4
6
8
10
12
14
16
18
20
22
x2
x1
x3
x4
显然,
x3,x4满足不等式12≤x≤20
,而x1,x2不满足,
当水位在15m,19m时,发电机能正常工作,
当水位在8m,10m时,发电机不能正常工作。
新知应用
(2)当水位在下列位置时,发电机能正常工作吗?
①x1=8;②x2=10;③x3=15;④x4=19.
用不等式和数轴给出解释。
16
点在范围内
数满足不等式
发电机能正常工作
在数轴上表示不等式
和
的下列取值:
,并利用数轴说明,
的这些取值中,哪些满足不等式
,哪些不满足.
巩固练习
一、数学知识:
不等式的概念:用符号“<”(或“≤”),“>”(或“≥”),“≠”连接而成的数学式子叫做不等式。
二、数学技能:
1.列不等式
2.用数轴表示不等式
三、数学思想:
1.
分类思想
2.
类比思想
3.
数形结合
谢谢大家的参与!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
