浙教版八年级上册第1章 1.1三角形起始课 课件(共20张PPT)
文档属性
| 名称 | 浙教版八年级上册第1章 1.1三角形起始课 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-20 17:52:20 | ||
图片预览







文档简介
(共20张PPT)
“三角形”起始课
线段
角
相交线
平行线
三角形
一条线
两条线
三条线
射线
直线
B
A
●
●
A
B
●
●
●
●
B
A
几何图形
活动一:研究方向的确立
情景变式:请举出生活中的“三角形”。
活动一:研究方向的确立
画一画:画出一个三角形;
想一想:三角形有何共同特征?
活动二:研究思路的规划
回顾“线段和角”的研究过程,我们研究了哪些内容?是按怎样的路径展开研究的?
活动二:研究思路的规划
唤醒已有的知识与经验
学习要求:自主学习→小组学习→全班学习
在小学,我们学习了三角形的哪些内容?
活动二:研究思路的规划
唤醒已有的知识和经验
定义——表示——分类——度量——性质——特例
有公共端点的两条射线组成的图形叫做角。
活动三:研究过程的开展
思考:仿照“角”的定义,请对“三角形”下个定义。
类比活动1——定义
类比活动1——定义
操作实践:
拼一拼:拼出一个三角形。
做中思:
(1)是不是任意拼(画)三条线段,都能成为三角形?
(2)三条线段应该怎样拼接才能成为三角形?
活动三:研究过程的开展
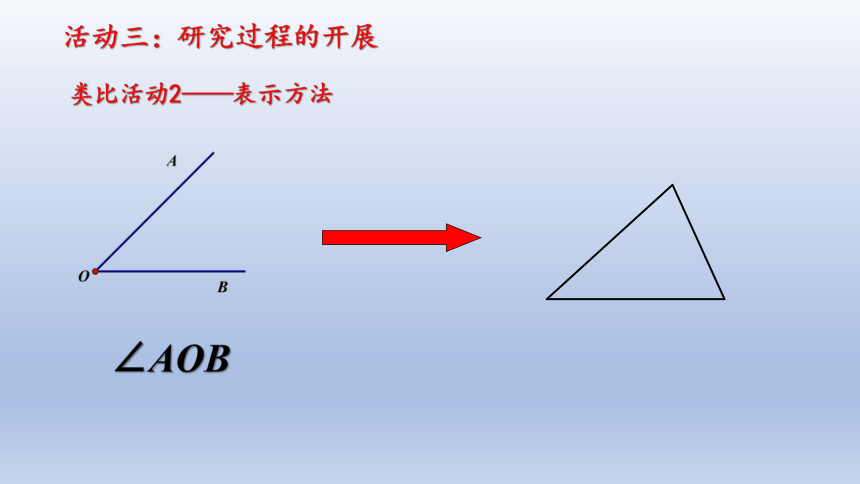
类比活动2——表示方法
∠AOB
活动三:研究过程的开展
类比活动3——三角形的分类
(1)
三边都相等的三角形叫做等边三角形(如图1)
(3)
三边都不相等的三角形叫做不等边三角形(如图3)
有两条边都相等的三角形叫做等腰三角形(如图2)
(2)
活动三:研究过程的开展
腰
腰
底边
顶角
底角
类比活动3——三角形的分类
直角
三角形
钝角
三角形
锐角
三角形
不等边三角形
等腰
三角形
等边
三角形
活动三:研究过程的开展
按角的大小分类
直角三角形
锐角三角形
钝角三角形
三角形
等边三角形
按边的相等关系分类
不等边三角形
等腰三角形
底边和腰不相等
的等腰三角形
三角形
b+c>a
①
a+b>c
②
a+c>b
③
●
●
探究:从点B出发,沿三角形的边到点C,有几条线路可以选择?
三角形两边的和大于第三边
三角形两边的差小于第三边
由②③移项得
a>c-b
a>b-c
类比活动4——性质
活动三:研究过程的开展
类比活动4——性质
经验迁移:猜想一下三角形还有哪些性质呢?
“图形的组成要素的相互关系就是性质”
活动三:研究过程的开展
类比活动5——度量
活动三:研究过程的开展
线段的长度可以用米、厘米等来刻画,
角的大小可以用度、分、秒来刻画,
猜想:对于“三角形”,你能想到什么?
类比活动6——特例
在“三角形”研究中,有哪些“特例(特殊关系)”值得研究呢?
活动三:研究过程的开展
答:图中有5个三角形,
它们是:△ABE、△BCE、△CDE
△ABC、△BCD
1.图中有几个三角形?用符号表示这些三角形。
变式:
以E为顶点的三角形有哪些?
△ABE、△BCE、△ECD
活动四:研究成果的运用
你是怎么找的?
(3)
6,5,11
(
)
(4)
12,7,6
(
)
2.下列长度的三条线段能否组成三角形?为什么?
(1)
3,8,4
(
)
(2)
7,4,5
(
)
不能
不能
能
能
思考:你是怎么判断三条线段能否组成三角形的?
解题策略:
只要满足较小的两条线段之和大于最长线段,
便可构成三角形;若不满足,则不能构成三角形.
3.请在下列横线上填一个数字,使得这三个长度的线段能构成三角形。
7
,4,
______。
3活动四:研究成果的运用
?
①本节课,我学到了哪些知识?
②本节课,给我感受最深的是什么?
③课后你准备对哪方面进行进一步研究?
还有哪些困惑?此外我还知道了……
活动五:研究活动的评价
定义—表示方法—分类—度量—性质—特例
怎样学
为何学
线段、角
三角形
类比
学什么
类比是一个伟大的引路人!
——美籍匈牙利数学家波利亚(GeorgePolya.1887-1985)
“三角形”起始课
线段
角
相交线
平行线
三角形
一条线
两条线
三条线
射线
直线
B
A
●
●
A
B
●
●
●
●
B
A
几何图形
活动一:研究方向的确立
情景变式:请举出生活中的“三角形”。
活动一:研究方向的确立
画一画:画出一个三角形;
想一想:三角形有何共同特征?
活动二:研究思路的规划
回顾“线段和角”的研究过程,我们研究了哪些内容?是按怎样的路径展开研究的?
活动二:研究思路的规划
唤醒已有的知识与经验
学习要求:自主学习→小组学习→全班学习
在小学,我们学习了三角形的哪些内容?
活动二:研究思路的规划
唤醒已有的知识和经验
定义——表示——分类——度量——性质——特例
有公共端点的两条射线组成的图形叫做角。
活动三:研究过程的开展
思考:仿照“角”的定义,请对“三角形”下个定义。
类比活动1——定义
类比活动1——定义
操作实践:
拼一拼:拼出一个三角形。
做中思:
(1)是不是任意拼(画)三条线段,都能成为三角形?
(2)三条线段应该怎样拼接才能成为三角形?
活动三:研究过程的开展
类比活动2——表示方法
∠AOB
活动三:研究过程的开展
类比活动3——三角形的分类
(1)
三边都相等的三角形叫做等边三角形(如图1)
(3)
三边都不相等的三角形叫做不等边三角形(如图3)
有两条边都相等的三角形叫做等腰三角形(如图2)
(2)
活动三:研究过程的开展
腰
腰
底边
顶角
底角
类比活动3——三角形的分类
直角
三角形
钝角
三角形
锐角
三角形
不等边三角形
等腰
三角形
等边
三角形
活动三:研究过程的开展
按角的大小分类
直角三角形
锐角三角形
钝角三角形
三角形
等边三角形
按边的相等关系分类
不等边三角形
等腰三角形
底边和腰不相等
的等腰三角形
三角形
b+c>a
①
a+b>c
②
a+c>b
③
●
●
探究:从点B出发,沿三角形的边到点C,有几条线路可以选择?
三角形两边的和大于第三边
三角形两边的差小于第三边
由②③移项得
a>c-b
a>b-c
类比活动4——性质
活动三:研究过程的开展
类比活动4——性质
经验迁移:猜想一下三角形还有哪些性质呢?
“图形的组成要素的相互关系就是性质”
活动三:研究过程的开展
类比活动5——度量
活动三:研究过程的开展
线段的长度可以用米、厘米等来刻画,
角的大小可以用度、分、秒来刻画,
猜想:对于“三角形”,你能想到什么?
类比活动6——特例
在“三角形”研究中,有哪些“特例(特殊关系)”值得研究呢?
活动三:研究过程的开展
答:图中有5个三角形,
它们是:△ABE、△BCE、△CDE
△ABC、△BCD
1.图中有几个三角形?用符号表示这些三角形。
变式:
以E为顶点的三角形有哪些?
△ABE、△BCE、△ECD
活动四:研究成果的运用
你是怎么找的?
(3)
6,5,11
(
)
(4)
12,7,6
(
)
2.下列长度的三条线段能否组成三角形?为什么?
(1)
3,8,4
(
)
(2)
7,4,5
(
)
不能
不能
能
能
思考:你是怎么判断三条线段能否组成三角形的?
解题策略:
只要满足较小的两条线段之和大于最长线段,
便可构成三角形;若不满足,则不能构成三角形.
3.请在下列横线上填一个数字,使得这三个长度的线段能构成三角形。
7
,4,
______。
3
?
①本节课,我学到了哪些知识?
②本节课,给我感受最深的是什么?
③课后你准备对哪方面进行进一步研究?
还有哪些困惑?此外我还知道了……
活动五:研究活动的评价
定义—表示方法—分类—度量—性质—特例
怎样学
为何学
线段、角
三角形
类比
学什么
类比是一个伟大的引路人!
——美籍匈牙利数学家波利亚(GeorgePolya.1887-1985)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
