2021-2022学年浙教新版九年级上册数学《第4章 相似三角形》单元测试卷(word、解析版)
文档属性
| 名称 | 2021-2022学年浙教新版九年级上册数学《第4章 相似三角形》单元测试卷(word、解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 317.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-24 17:16:51 | ||
图片预览




文档简介
2021-2022学年浙教新版九年级上册数学《第4章
相似三角形》单元测试卷
一.选择题
1.如果=,那么的值为( )
A.
B.
C.
D.
2.如果ab=cd,则下列正确得是( )
A.a:c=b:d
B.a:d=c:b
C.a:b=c:d
D.d:c=b:a
3.下列说法正确的是( )
A.所有等边三角形都相似
B.有一个角相等的两个等腰三角形相似
C.所有直角三角形都相似
D.所有矩形都相似
4.如图,在△ABC中,点D是AB上一点,DE∥BC交AC于点E,AD=3,BD=2,则AE与EC的比是( )
A.9:4
B.3:5
C.9:16
D.3:2
5.已知△ABC∽△A′B′C′,,则△ABC与△A′B′C′的面积之比为( )
A.
B.
C.
D.
6.甲数:乙数=3:2,乙数:丙数=5:6,丙数:甲数=( )
A.2:1
B.5:3
C.4:5
D.5:4
7.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DF=6,则EF的长为( )
A.4
B.4.5
C.5
D.5.5
8.已知△ABC∽△DEF,相似比为1:2,且△DEF的面积为12,则△ABC的面积为( )
A.84
B.24
C.6
D.3
9.某零件长40厘米,若该零件在设计图上的长是2毫米,则这幅设计图的比例尺是( )
A.1:2000
B.1:200
C.200:1
D.2000:1
10.点B把线段AC分成两部分,如果==k,那么k的值为( )
A.
B.
C.
+1
D.﹣1
二.填空题
11.若==,a﹣b+c=18,则a的值为
.
12.已知4x﹣5y=0,则x:y的值为
.
13.若△ABC∽△DEF,且△ABC与△DEF的面积之比为1:9,则△ABC与△DEF的相似比为
.
14.已知,则的值为
.
15.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则DF的长是
.
16.如图,a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB=6,BC=9,DF=12,则EF=
.
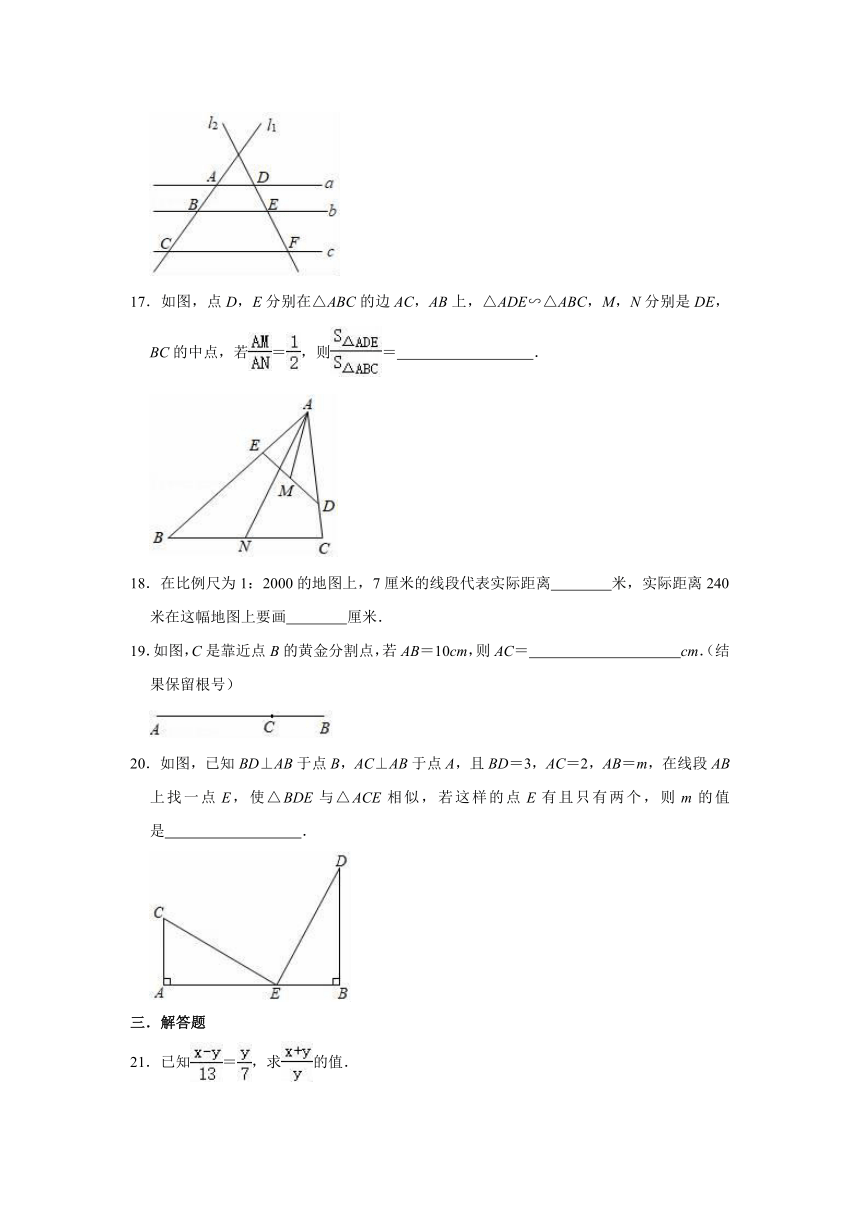
17.如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若=,则=
.
18.在比例尺为1:2000的地图上,7厘米的线段代表实际距离
米,实际距离240米在这幅地图上要画
厘米.
19.如图,C是靠近点B的黄金分割点,若AB=10cm,则AC=
cm.(结果保留根号)
20.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是
.
三.解答题
21.已知=,求的值.
22.已知:,求的值.
23.已知:,求a:b:c的值.
24.(1)已知a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,求线段d的长.
(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段a和b的比例中项.求线段c的长.
(3)已知y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4,x=2时,y=5.
求:①y与x之间的函数关系式;②当x=4时,求y的值.
25.如图,在△ABC中,D、E分别是AB和BC上的点,且DE∥AC,=,=,求.
26.如图,点C将线段AB分成两部分,若AC2=BC?AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
参考答案与试题解析
一.选择题
1.解:根据比例的基本性质得:
5x=3(x+y),即2x=3y,
即得=.
故选:A.
2.解:A、a:c=b:d?ad=cb,故错误;
B、a:d=c:b?ab=cd,故正确;
C、a:b=c:d?ad=cb,故错误;
D、d:c=b:a?da=cb,故错误.
故选:B.
3.解:(A)等边三角形各内角为60°,各边长相等,所以所有的等边三角形均相似,故本选项正确;
(B)一对等腰三角形中,若底角和顶角相等且不等于60°,则该对三角形不相似,故本选项错误;
(C)直角三角形中的两个锐角的大小不确定,无法判定三角形相似,故本选项错误;
(D)矩形的邻边的关系不确定,所以并不是所有矩形都相似,故本选项错误.
故选:A.
4.解:∵DE∥BC,AD=3,BD=2,
∴==,
故选:D.
5.解:∵△ABC∽△A′B′C′,,
∴△ABC与△A′B′C′的面积比=()2=,
故选:C.
6.解:2和5的最小公倍数是10,
甲数:乙数=3:2=15:10,
乙数:丙数=5:6=10:12,
丙数:甲数=12:15=4:5.
故选:C.
7.解:∵AD∥BE∥CF,
∴=,即=,
解得,EF=4.5,
故选:B.
8.解:∵△ABC∽△DEF,相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
∵△DEF的面积为12,
∴△ABC的面积为3,
故选:D.
9.解:因为2毫米=0.2厘米,
则0.2厘米:40厘米=1:200;
所以这幅设计图的比例尺是1:200.
故选:B.
10.解:∵点B把线段AC分成两部分,==k,
∴点B是线段AC的黄金分割点,AB>BC,
∴k=,
故选:B.
二.填空题
11.解:设===k,
则a=2k,b=3k,c=4k,
∵a﹣b+c=18,
∴2k﹣3k+4k=18,
解得k=6,
∴a=2k=12.
故答案为:12.
12.解:∵4x﹣5y=0,
∴4x=5y,
∴=;
故答案为:.
13.解:∵△ABC∽△DEF,△ABC与△DEF的面积之比为1:9,
∴△ABC与△DEF的相似比为1:3,
故答案为:1:3.
14.解:设b=3k,则a=2k,
则==﹣.
故答案为:﹣.
15.解:∵l1∥l2∥l3,=,
∴==,即=,
解得,EF=6,
∴DF=DE+EF=10,
故答案为:10.
16.解:∵a∥b∥c,
∴=,即=,
解得,EF=7.2,
故答案为:7.2.
17.解:∵M,N分别是DE,BC的中点,
∴AM、AN分别为△ADE、△ABC的中线,
∵△ADE∽△ABC,
∴==,
∴=()2=,
故答案为:.
18.解:7÷=14000(厘米),
14000厘米=140米;
240米=24000厘米,
24000×=12(厘米).
答:7厘米的线段代表实际距离140米,实际距离240米在这幅地图上要画12厘米.
故答案为:140;12.
19.解:∵C是靠近点B的黄金分割点,AB=10cm,
∴AC>BC,AC=AB=×10=(5﹣5)cm,
故答案为:(5﹣5).
20.解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
分两种情况:
(1)当∠ACE=∠BDE时,△ACE∽△BDE,
∴==,
∴AE=BE①,
当∠ACE=∠BED时,△ACE∽△BED,
∴=,
即AE×BE=AC×BD=2×3=6②,
由①②得:
BE2=6,
解得:BE=3,
∴AE=2,
∴AB=AE+BE=5,即m=5;
当AE=2时,BE=3,两个三角形相似;
当AE=3时,BE=2,两个三角形全等,符合题目要求;
(2)设AE=x,则BE=m﹣x,
当∠ACE=∠BED时,△ACE∽△BED,
∴=,
∴x:3=2:(m﹣x),
整理得:x2﹣mx+6=0,
方程有唯一解时,△=m2﹣24=0,
解得:m=±2(负值舍去),
∴m=2;
当m=2时,
AE:BE=2:3时,两个三角形相似;
AE=BE=时,两个三角形相似;同样是两个点可以满足要求;
综上所述,△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是5或2;
故答案为:5或2.
三.解答题
21.解:=,
7x﹣7y=13y
x=y,
则==.
22.解:
∵,
∴5(3b﹣a)=3(3a﹣2b),
整理可得:3b=2a,
∴=.
23.解:设=k,则a+b=10k,b+c=11k,c+a=15k,解得:a=7k,b=3k,c=8k.
a:b:c=7:3:8.
24.解:(1)∵a、b、c、d是成比例线段,
∴=,
∵a=3,b=2,c=6,
代入得:d=4,
答:线段d的长是4cm.
(2)解:∵线段c是线段
a和b的比例中项,
∴c2=ab,
∵a=4,b=9,代入得:c=6,
答:线段c的长是6cm.
(3)①解:∵y1与x成正比例,
设y1=ax,(a≠0),
∵y2与x成反比例,
设y2=(b≠0)
∴y=ax+,
把x=1,y=4和x=2,y=5代入得:
,
解得:,
∴y=2x+,
答:y与x之间的函数关系式是y=2x+.
②解:由①知:y=2x+,
当x=4时,y=,
答:当x=4时,y的值是.
25.解:
∵=,
∴=,
∵DE∥AC,
∴,
∴.
26.解:(Ⅰ)∵黄金抛物线的对称轴是直线x=2,
∴﹣=2,
∴b=﹣4a,又b2=ac
∴16a2=ac.
且与y轴交于点(0,8),
∴c=8.
∴a=,b=﹣2.
∴y=x2﹣2x+8
=(x﹣2)2+6,
∵>0,
∴y有最小值为6.
答:y的最小值为6.
(Ⅱ)原点是线段AB的黄金分割点.理由如下:
∵黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),
把它向下平移后与x轴交于A(+3,0),B(x0,0),
∴x0=﹣1﹣.
∴OA=3+,OB=1+,AB=4+2.
OA2=(3+)2=14+6.
OB?AB=(1+
)(4+2)=14+6.
∴OA2=OB?AB.
答:原点是线段AB的黄金分割点.
相似三角形》单元测试卷
一.选择题
1.如果=,那么的值为( )
A.
B.
C.
D.
2.如果ab=cd,则下列正确得是( )
A.a:c=b:d
B.a:d=c:b
C.a:b=c:d
D.d:c=b:a
3.下列说法正确的是( )
A.所有等边三角形都相似
B.有一个角相等的两个等腰三角形相似
C.所有直角三角形都相似
D.所有矩形都相似
4.如图,在△ABC中,点D是AB上一点,DE∥BC交AC于点E,AD=3,BD=2,则AE与EC的比是( )
A.9:4
B.3:5
C.9:16
D.3:2
5.已知△ABC∽△A′B′C′,,则△ABC与△A′B′C′的面积之比为( )
A.
B.
C.
D.
6.甲数:乙数=3:2,乙数:丙数=5:6,丙数:甲数=( )
A.2:1
B.5:3
C.4:5
D.5:4
7.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.已知AB=1,BC=3,DF=6,则EF的长为( )
A.4
B.4.5
C.5
D.5.5
8.已知△ABC∽△DEF,相似比为1:2,且△DEF的面积为12,则△ABC的面积为( )
A.84
B.24
C.6
D.3
9.某零件长40厘米,若该零件在设计图上的长是2毫米,则这幅设计图的比例尺是( )
A.1:2000
B.1:200
C.200:1
D.2000:1
10.点B把线段AC分成两部分,如果==k,那么k的值为( )
A.
B.
C.
+1
D.﹣1
二.填空题
11.若==,a﹣b+c=18,则a的值为
.
12.已知4x﹣5y=0,则x:y的值为
.
13.若△ABC∽△DEF,且△ABC与△DEF的面积之比为1:9,则△ABC与△DEF的相似比为
.
14.已知,则的值为
.
15.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若=,DE=4,则DF的长是
.
16.如图,a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB=6,BC=9,DF=12,则EF=
.
17.如图,点D,E分别在△ABC的边AC,AB上,△ADE∽△ABC,M,N分别是DE,BC的中点,若=,则=
.
18.在比例尺为1:2000的地图上,7厘米的线段代表实际距离
米,实际距离240米在这幅地图上要画
厘米.
19.如图,C是靠近点B的黄金分割点,若AB=10cm,则AC=
cm.(结果保留根号)
20.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=3,AC=2,AB=m,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是
.
三.解答题
21.已知=,求的值.
22.已知:,求的值.
23.已知:,求a:b:c的值.
24.(1)已知a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,求线段d的长.
(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段a和b的比例中项.求线段c的长.
(3)已知y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4,x=2时,y=5.
求:①y与x之间的函数关系式;②当x=4时,求y的值.
25.如图,在△ABC中,D、E分别是AB和BC上的点,且DE∥AC,=,=,求.
26.如图,点C将线段AB分成两部分,若AC2=BC?AB(AC>BC),则称点C为线段AB的黄金分割点.某数学兴趣小组在进行抛物线课题研究时,由黄金分割点联想到“黄金抛物线”,类似地给出“黄金抛物线”的定义:若抛物线y=ax2+bx+c,满足b2=ac(b≠0),则称此抛物线为黄金抛物线.
(Ⅰ)若某黄金抛物线的对称轴是直线x=2,且与y轴交于点(0,8),求y的最小值;
(Ⅱ)若黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),把它向下平移后与x轴交于A(+3,0),B(x0,0),判断原点是否是线段AB的黄金分割点,并说明理由.
参考答案与试题解析
一.选择题
1.解:根据比例的基本性质得:
5x=3(x+y),即2x=3y,
即得=.
故选:A.
2.解:A、a:c=b:d?ad=cb,故错误;
B、a:d=c:b?ab=cd,故正确;
C、a:b=c:d?ad=cb,故错误;
D、d:c=b:a?da=cb,故错误.
故选:B.
3.解:(A)等边三角形各内角为60°,各边长相等,所以所有的等边三角形均相似,故本选项正确;
(B)一对等腰三角形中,若底角和顶角相等且不等于60°,则该对三角形不相似,故本选项错误;
(C)直角三角形中的两个锐角的大小不确定,无法判定三角形相似,故本选项错误;
(D)矩形的邻边的关系不确定,所以并不是所有矩形都相似,故本选项错误.
故选:A.
4.解:∵DE∥BC,AD=3,BD=2,
∴==,
故选:D.
5.解:∵△ABC∽△A′B′C′,,
∴△ABC与△A′B′C′的面积比=()2=,
故选:C.
6.解:2和5的最小公倍数是10,
甲数:乙数=3:2=15:10,
乙数:丙数=5:6=10:12,
丙数:甲数=12:15=4:5.
故选:C.
7.解:∵AD∥BE∥CF,
∴=,即=,
解得,EF=4.5,
故选:B.
8.解:∵△ABC∽△DEF,相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
∵△DEF的面积为12,
∴△ABC的面积为3,
故选:D.
9.解:因为2毫米=0.2厘米,
则0.2厘米:40厘米=1:200;
所以这幅设计图的比例尺是1:200.
故选:B.
10.解:∵点B把线段AC分成两部分,==k,
∴点B是线段AC的黄金分割点,AB>BC,
∴k=,
故选:B.
二.填空题
11.解:设===k,
则a=2k,b=3k,c=4k,
∵a﹣b+c=18,
∴2k﹣3k+4k=18,
解得k=6,
∴a=2k=12.
故答案为:12.
12.解:∵4x﹣5y=0,
∴4x=5y,
∴=;
故答案为:.
13.解:∵△ABC∽△DEF,△ABC与△DEF的面积之比为1:9,
∴△ABC与△DEF的相似比为1:3,
故答案为:1:3.
14.解:设b=3k,则a=2k,
则==﹣.
故答案为:﹣.
15.解:∵l1∥l2∥l3,=,
∴==,即=,
解得,EF=6,
∴DF=DE+EF=10,
故答案为:10.
16.解:∵a∥b∥c,
∴=,即=,
解得,EF=7.2,
故答案为:7.2.
17.解:∵M,N分别是DE,BC的中点,
∴AM、AN分别为△ADE、△ABC的中线,
∵△ADE∽△ABC,
∴==,
∴=()2=,
故答案为:.
18.解:7÷=14000(厘米),
14000厘米=140米;
240米=24000厘米,
24000×=12(厘米).
答:7厘米的线段代表实际距离140米,实际距离240米在这幅地图上要画12厘米.
故答案为:140;12.
19.解:∵C是靠近点B的黄金分割点,AB=10cm,
∴AC>BC,AC=AB=×10=(5﹣5)cm,
故答案为:(5﹣5).
20.解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
分两种情况:
(1)当∠ACE=∠BDE时,△ACE∽△BDE,
∴==,
∴AE=BE①,
当∠ACE=∠BED时,△ACE∽△BED,
∴=,
即AE×BE=AC×BD=2×3=6②,
由①②得:
BE2=6,
解得:BE=3,
∴AE=2,
∴AB=AE+BE=5,即m=5;
当AE=2时,BE=3,两个三角形相似;
当AE=3时,BE=2,两个三角形全等,符合题目要求;
(2)设AE=x,则BE=m﹣x,
当∠ACE=∠BED时,△ACE∽△BED,
∴=,
∴x:3=2:(m﹣x),
整理得:x2﹣mx+6=0,
方程有唯一解时,△=m2﹣24=0,
解得:m=±2(负值舍去),
∴m=2;
当m=2时,
AE:BE=2:3时,两个三角形相似;
AE=BE=时,两个三角形相似;同样是两个点可以满足要求;
综上所述,△BDE与△ACE相似,若这样的点E有且只有两个,则m的值是5或2;
故答案为:5或2.
三.解答题
21.解:=,
7x﹣7y=13y
x=y,
则==.
22.解:
∵,
∴5(3b﹣a)=3(3a﹣2b),
整理可得:3b=2a,
∴=.
23.解:设=k,则a+b=10k,b+c=11k,c+a=15k,解得:a=7k,b=3k,c=8k.
a:b:c=7:3:8.
24.解:(1)∵a、b、c、d是成比例线段,
∴=,
∵a=3,b=2,c=6,
代入得:d=4,
答:线段d的长是4cm.
(2)解:∵线段c是线段
a和b的比例中项,
∴c2=ab,
∵a=4,b=9,代入得:c=6,
答:线段c的长是6cm.
(3)①解:∵y1与x成正比例,
设y1=ax,(a≠0),
∵y2与x成反比例,
设y2=(b≠0)
∴y=ax+,
把x=1,y=4和x=2,y=5代入得:
,
解得:,
∴y=2x+,
答:y与x之间的函数关系式是y=2x+.
②解:由①知:y=2x+,
当x=4时,y=,
答:当x=4时,y的值是.
25.解:
∵=,
∴=,
∵DE∥AC,
∴,
∴.
26.解:(Ⅰ)∵黄金抛物线的对称轴是直线x=2,
∴﹣=2,
∴b=﹣4a,又b2=ac
∴16a2=ac.
且与y轴交于点(0,8),
∴c=8.
∴a=,b=﹣2.
∴y=x2﹣2x+8
=(x﹣2)2+6,
∵>0,
∴y有最小值为6.
答:y的最小值为6.
(Ⅱ)原点是线段AB的黄金分割点.理由如下:
∵黄金抛物线y=ax2+bx+c(a>0)的顶点P为(1,3),
把它向下平移后与x轴交于A(+3,0),B(x0,0),
∴x0=﹣1﹣.
∴OA=3+,OB=1+,AB=4+2.
OA2=(3+)2=14+6.
OB?AB=(1+
)(4+2)=14+6.
∴OA2=OB?AB.
答:原点是线段AB的黄金分割点.
同课章节目录
