矩形、菱形、正方形复习

矩形、菱形、正方形复习
姓名
学习重难点
【重点】掌握并会灵活运用平行四边形的定义、性质及判定；会灵活应用平行四边形及特殊平行四边形的相关知识解决一些简单的实际问题；并会灵活运用；理解并掌握三角形中位线的定义及性质，会应用它们解决一些计算及实际问题.
【难点】掌握平行四边形、矩形、菱形、正方形、性质及判定条件，以及它们之间存在的联系与区别，会应用三角形中位线解决一些简单问题.
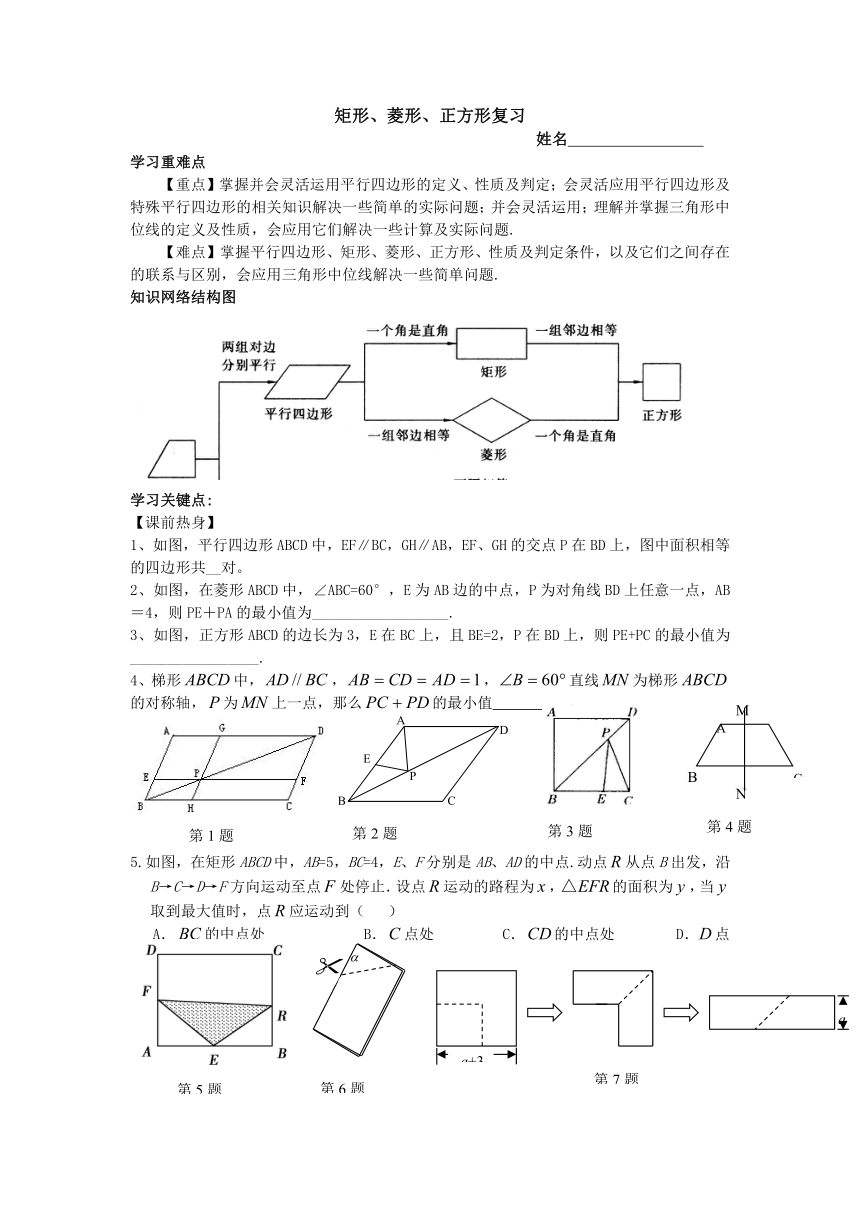
知识网络结构图
学习关键点:
【课前热身】
1、如图，平行四边形ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上，图中面积相等的四边形共__对。
2、如图，在菱形ABCD中，∠ABC=60°，E为AB边的中点，P为对角线BD上任意一点，AB＝4，则PE＋PA的最小值为__________________.
3、如图，正方形ABCD的边长为3，E在BC上，且BE=2，P在BD上，则PE+PC的最小值为_________________.
4、梯形中，，，直线为梯形的对称轴，为上一点，那么的最小值 。
5.如图，在矩形ABCD中，AB=5，BC=4，E、F分别是AB、AD的中点.动点从点B出发，沿B→C→D→F方向运动至点处停止．设点运动的路程为，的面积为，当取到最大值时，点应运动到（ ）
A．的中点处 B．点处 C．的中点处 D．点处
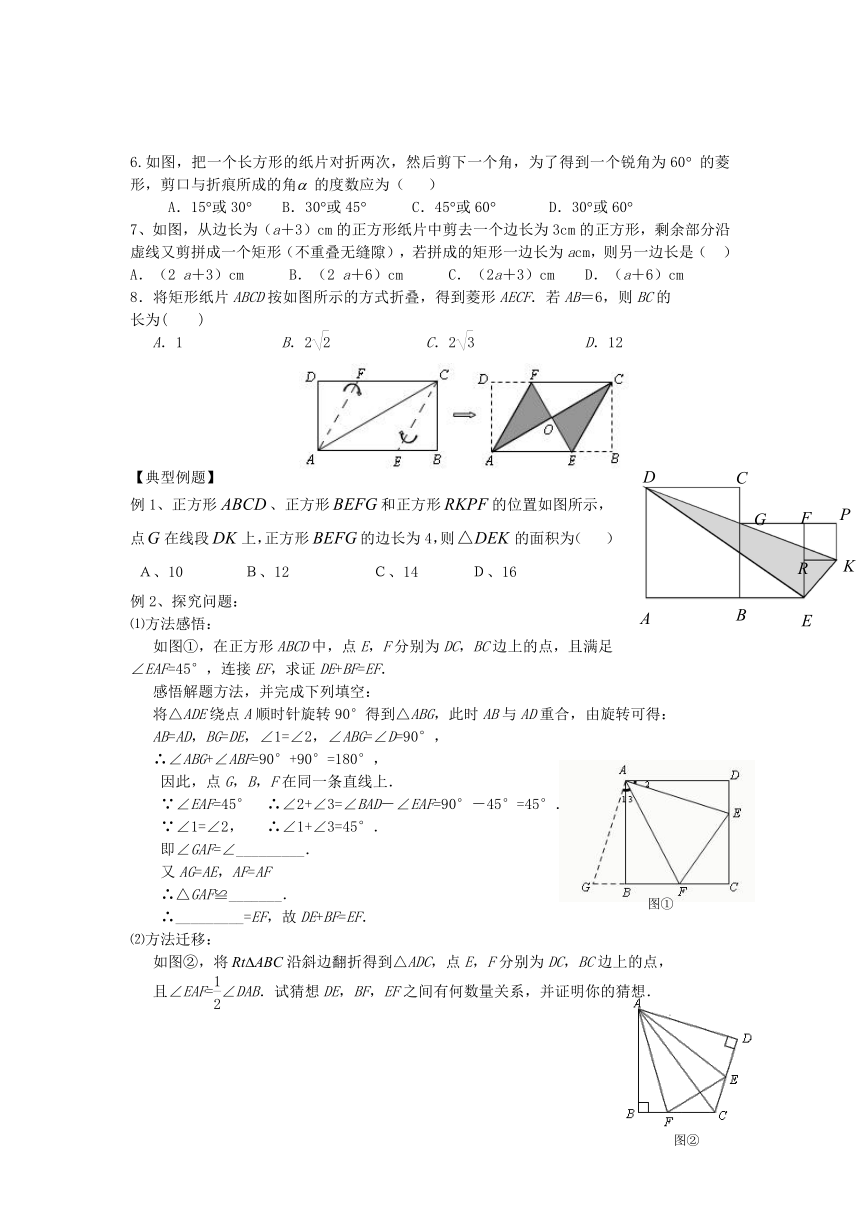
6.如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个锐角为60 的菱形，剪口与折痕所成的角 的度数应为（ ）
A．15或30 B．30或45 C．45或60 D．30或60
7、如图，从边长为（a＋3）cm的正方形纸片中剪去一个边长为3cm的正方形，剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），若拼成的矩形一边长为acm，则另一边长是（ ）
A．（2 a＋3）cm B．（2 a＋6）cm C．（2a＋3）cm D．（a＋6）cm
8．将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB＝6，则BC的长为( )
A．1 B．2 C．2 D．12
【典型例题】
例1、正方形、正方形和正方形的位置如图所示，点在线段上，正方形的边长为4，则的面积为（ ）
Ａ、10　　 Ｂ、12 Ｃ、14　　 　Ｄ、16
例2、探究问题：
⑴方法感悟：
如图①，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．
感悟解题方法，并完成下列填空：
将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：
AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，点G，B，F在同一条直线上．
∵∠EAF=45° ∴∠2+∠3=∠BAD－∠EAF=90°－45°=45°．
∵∠1=∠2， ∴∠1+∠3=45°．
即∠GAF=∠_________．
又AG=AE，AF=AF
∴△GAF≌_______．
∴_________=EF，故DE+BF=EF．
⑵方法迁移：
如图②，将沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，
且∠EAF=∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．
⑶问题拓展：
如图③，在四边形ABCD中，AB=AD，E，F分别为DC,BC上的点，满足∠EAF=∠DAB，试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）．
例3、已知正方形的边长为1，点、分别是边、
的两点，若的周长为2.
求： 的大小；
例4、某市要在一块形状为平行四边形ABCD的空地上建造一个四边形花园，要求花园所占面积是平行四边形ABCD面积的一半，并且四边形花园的四个顶点作为出入口，要求其分别在平行四边形ABCD的四条边上，请你设计两种方案.
例5、取一张矩形的纸进行折叠，具体操作过程如下：
第一步：先把矩形ABCD对折，折痕为MN，如图1；
第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B′，得Rt△AB'E，如图2；
第三步：沿EB'线折叠得折痕EF，如图3．
利用展开图4探究：
(1)△AEF是什么三角形 证明你的结论．
(2)对于任一矩形，按照上述方法是否都能折出这种三角形 请说明理由．
【反馈练习】
1.如图，在矩形ABCD中，AD =4，DC =3，将△ADC绕点A按逆时针方向旋转到△AEF（点A、B、E在同一直线上），则C点运动的路线的长度为 .
2.如图所示，正方形的面积为12，是等边三角形，点在正方形内，在对角线上有一点，使的和最小，则这个最小值为 .
3.如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB＝65°，则∠AED′= °.
4．一张矩形纸片经过折叠得到一个三角形（如图），则矩形的长与宽的比为 ．
5、（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．
下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．
证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．
∴∠NMC=180°—∠AMN —∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．
（下面请你完成余下的证明过程）
（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．
（3）若将（1）中的“正方形ABCD”改为“正边形ABCD……X”，请你作出猜想：
当∠AMN= °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）
第1题
第2题
第3题
A
B
M
N
C
第4题
a+3
a
第7题
第5题
第6题
图①
图②
图③
C
N
D
M
B
A
第3题
A
D
C
B
E
F
(第1题图)
A
D
E
P
B
C
第2题
E
D
B
C′
F
C
D′
A
第3题
（第4题图）