矩形、菱形、正方形复习

矩形、菱形、正方形复习
姓名
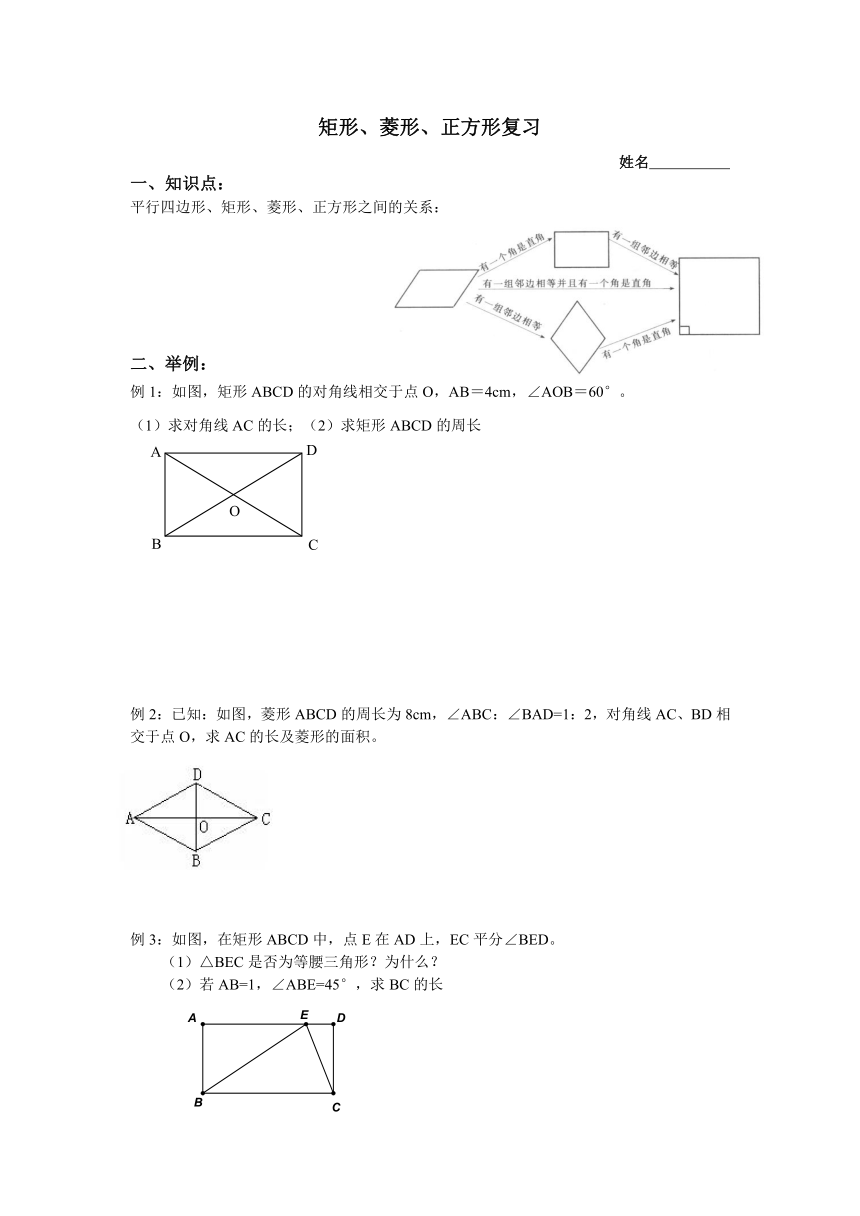
一、知识点：
平行四边形、矩形、菱形、正方形之间的关系：
二、举例：
例1：如图，矩形ABCD的对角线相交于点O，AB＝4cm，∠AOB＝60°。
（1）求对角线AC的长；（2）求矩形ABCD的周长
例2：已知：如图，菱形ABCD的周长为8cm，∠ABC：∠BAD=1：2，对角线AC、BD相交于点O，求AC的长及菱形的面积。
例3：如图，在矩形ABCD中，点E在AD上，EC平分∠BED。
（1）△BEC是否为等腰三角形？为什么？
（2）若AB=1，∠ABE=45°，求BC的长
例4：如图，在四边形ABCD中，AD∥BC，对角线AC的垂直平分线与边AD、BC分别相交于点E、F。四边形AFCE是菱形吗？为什么？
例5：如图，在菱形ABCD中，∠ABC=60°，E为AB边的中点，P为对角线BD上任意一点，AB＝4，则PE＋PA的最小值为__________________.
例6： (1) 如图1,在正方形ABCD中,点E、F分别在边BC、CD上，AE、BF交于点O，∠AOF＝90°.
求证：BE＝CF.
(2) 如图2，在正方形ABCD中，点E、H、F、G分别在边AB、BC、CD、DA上，EF、GH交于点O，∠FOH＝90°， EF＝4.求GH的长.
(3) 已知点E、H、F,、G分别在矩形ABCD的边AB、BC、CD、DA上，EF、GH交于点O，
∠FOH＝90°，EF＝4. 直接写出下列两题的答案：
①如图3，矩形ABCD由2个全等的正方形组成,求GH的长；
②如图4，矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
三、练习：
1、如图，矩形ABCD中，AE平分∠BAD，交BC于E，对角线AC、BD交于O，若∠OAE＝15°。（1）试说明：OB＝BE；（2）求∠BOE的度数.
2、如图，将矩形ABCD沿着直线BD折叠使点C落在点 C＇处，BC＇交AD于E，AD=8，AB=4，求△BED的面积。
3、已知：如图，△ABC中，∠ACB=90°，CD是高，AE是角平分线，交CD于点F，
EG⊥AB，G为垂足。试说明四边形CEGF是菱形。
4、如图，在正方形ABCD中，点E、F分别在BC、CD上移动，但A到EF的距离AH始终保持与AB长相等，问在E、F移动过程中：
（1）∠EAF的大小是否有变化？请说明理由．
（2）△ECF的周长是否有变化？请说明理由．
5、操作：将一把三角尺放在边长为4的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q探究：设A、P两点间的距离为x．
（1）当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你的结论．
（2）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形 如果可能，指出所有可能的情况，并求出相应的x的值.
6、正方形ABCD中，点O是对角线DB的中点，点P是DB所在直线上的一个动点，PE⊥BC于E，PF⊥DC于F.
(1)当点P与点O重合时(如图①)，猜测AP与EF的数量及位置关系，并证明你的结论；
(2)当点P在线段DB上 (不与点D、O、B重合)时(如图②)，探究(1)中的结论是否成立？若成立，写出证明过程；若不成立，请说明理由；
(3)当点P在DB的延长线上时，请将图③补充完整，并判断(1)中的结论是否成立？若成立，直接写出结论；若不成立，请写出相应的结论.
7、正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上，分别连接BD、BF、FD，得到△BFD。
（1）在图①~图③中，若正方形CEFG的周长分别为1、3、4，且正方形ABCD的边长均为3，请通过计算填写下表：
正方形CEFG的边长 1 3 4
△BFD的面积
（2）若正方形CEFG的边长为a，正方形ABCD的边长为b，猜出S△BFD的大小，并结合图③证明你的猜想。
O
D
C
B
A
第5题
图2
图4
图3
O
D
C
B
A
E
C′
E
D
C
B
A
A
B
C
D
P
Q
E