相似三角形复习

(共31张PPT)
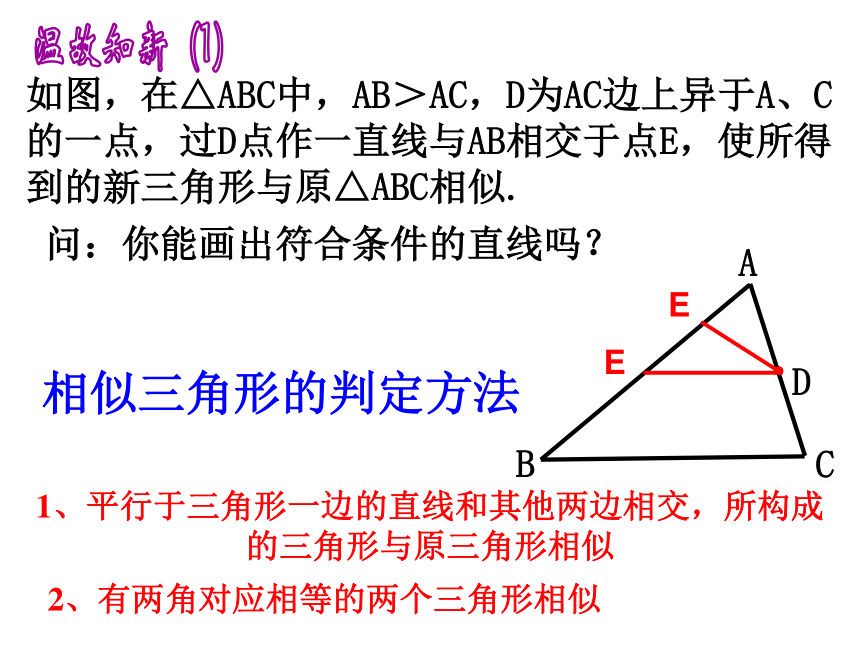
如图，在△ABC中，AB＞AC，D为AC边上异于A、C的一点，过D点作一直线与AB相交于点E，使所得到的新三角形与原△ABC相似.
问：你能画出符合条件的直线吗？
D
A
C
B
E
E
相似三角形的判定方法
1、平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似
2、有两角对应相等的两个三角形相似
A．
B．
C．
D．
A
B
C
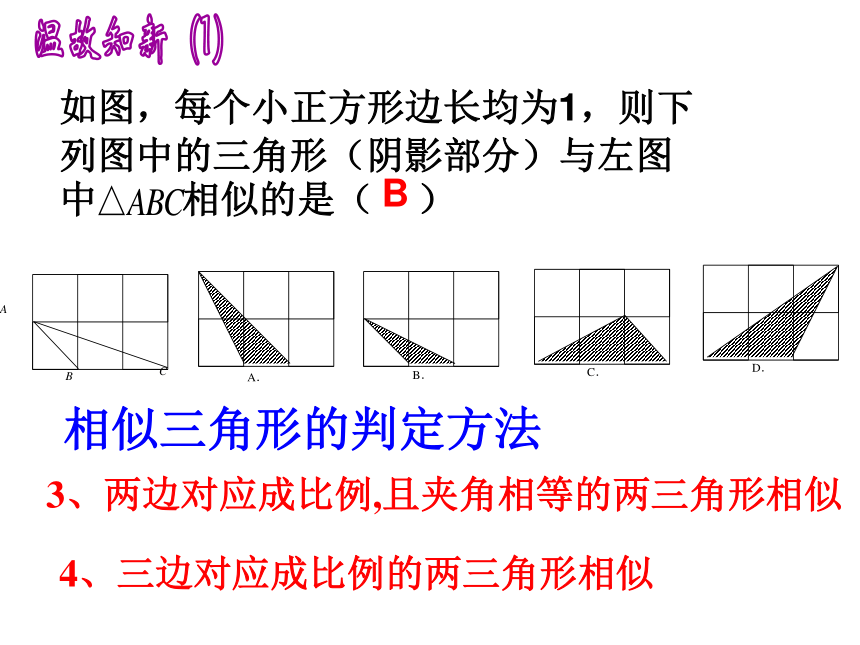
如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与左图中 相似的是（ ）
3、两边对应成比例,且夹角相等的两三角形相似
4、三边对应成比例的两三角形相似
B
相似三角形的判定方法
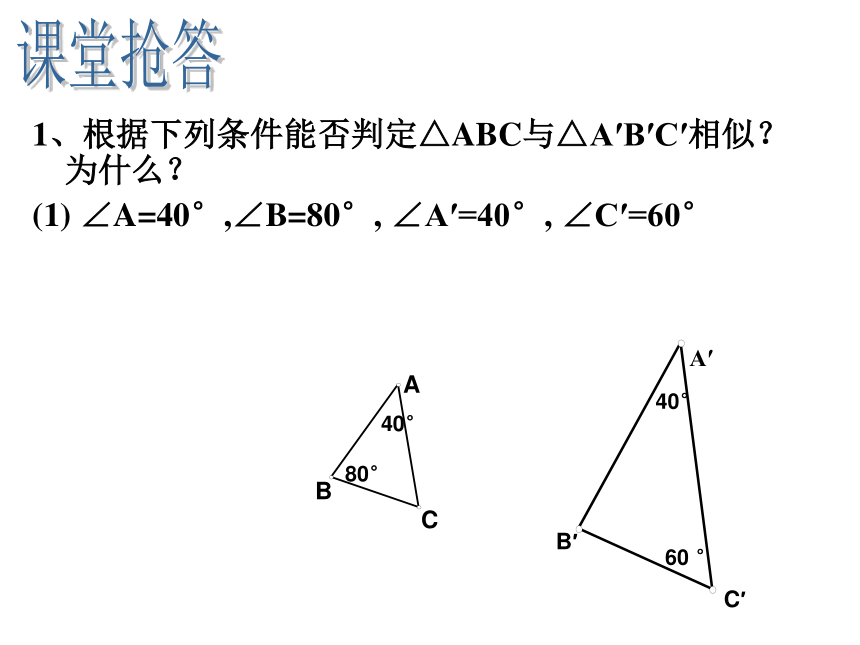
1、根据下列条件能否判定△ABC与△A′B′C′相似？为什么？
(1) ∠A=40°,∠B=80°, ∠A′=40°, ∠C′=60°
A
B
C
40°
80°
60 °
40°
A′
B′
C′
1、根据下列条件能否判定△ABC与△A′B′C′相似？为什么？
(2) ∠A=40°，AB=3 ，AC=6
∠A′=40°，A′B′=7 ，A′C′=14
7
A
B
C
40°
40°
A′
B′
C′
14
3
6
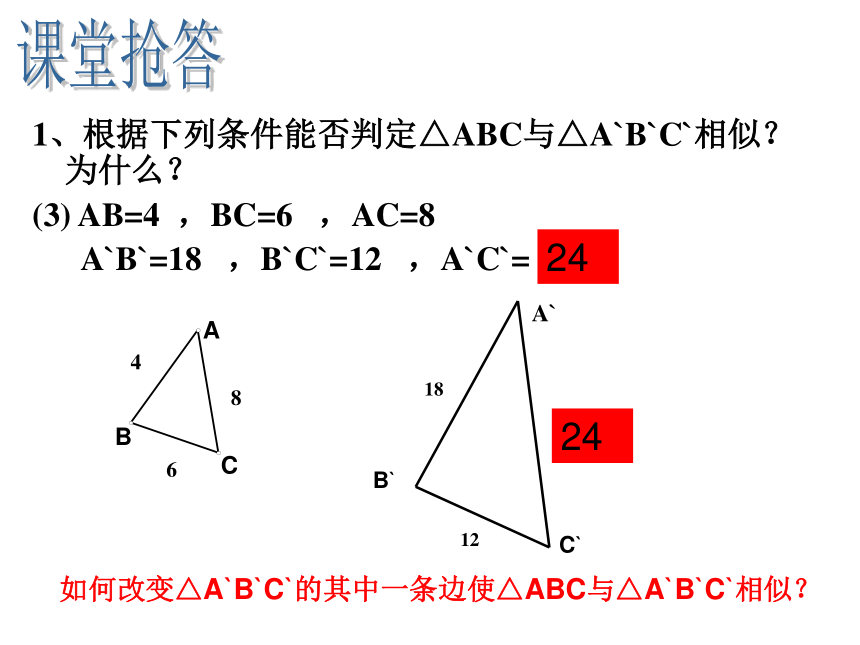
1、根据下列条件能否判定△ABC与△A`B`C`相似？为什么？
(3) AB=4 ，BC=6 ，AC=8
A`B`=18 ，B`C`=12 ，A`C`= 21
18
A
B
C
A`
B`
C`
21
4
8
6
12
24
24
如何改变△A`B`C`的其中一条边使△ABC与△A`B`C`相似？
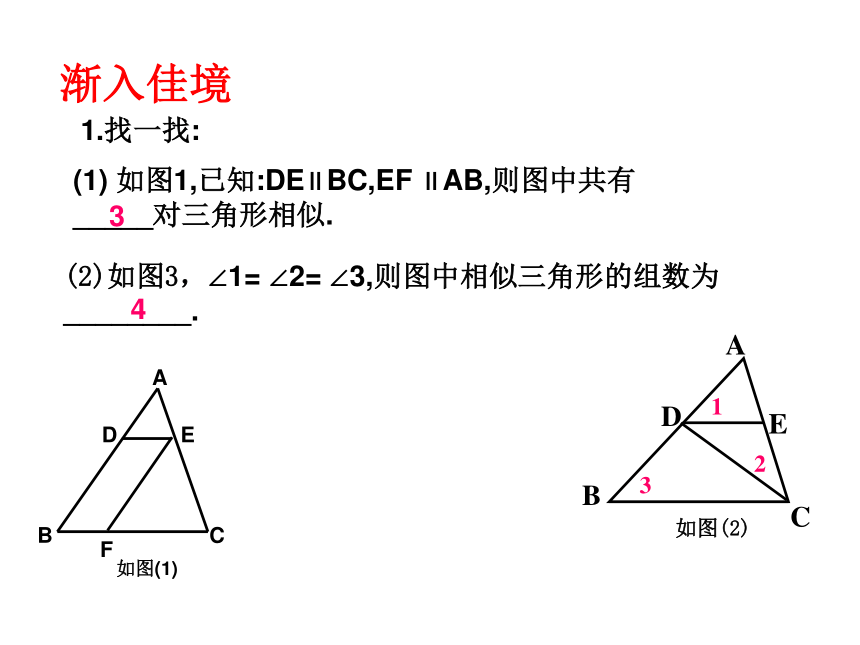
1.找一找:
(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有_____对三角形相似.
A
B
C
D
E
F
如图(1)
3
(2)如图3，∠1= ∠2= ∠3,则图中相似三角形的组数为
________.
A
D
B
E
C
1
3
2
如图(2)
4
渐入佳境
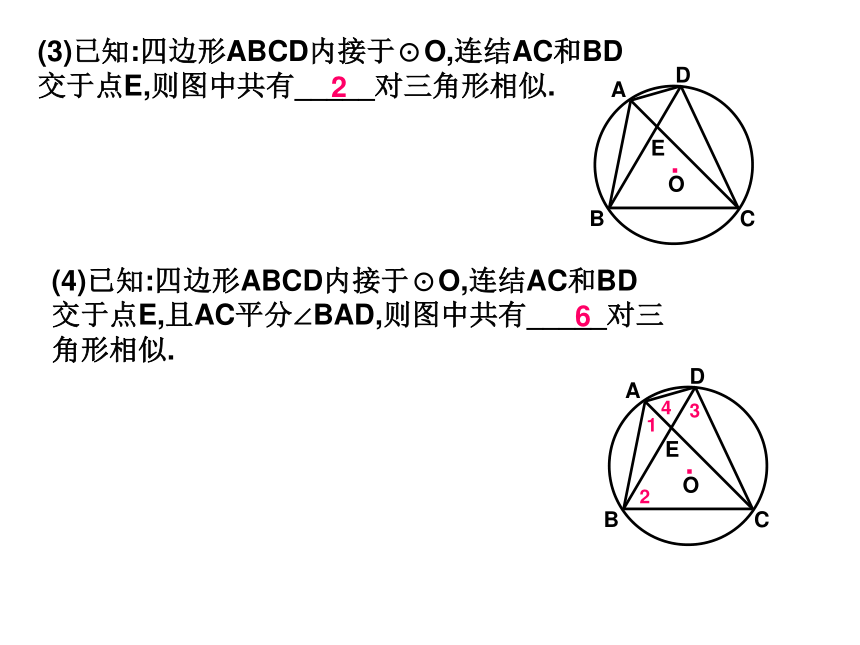
(3)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,则图中共有_____对三角形相似.
·
A
B
C
D
E
O
(4)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,且AC平分∠BAD,则图中共有_____对三角形相似.
·
A
B
C
D
E
O
1
2
3
4
6
2
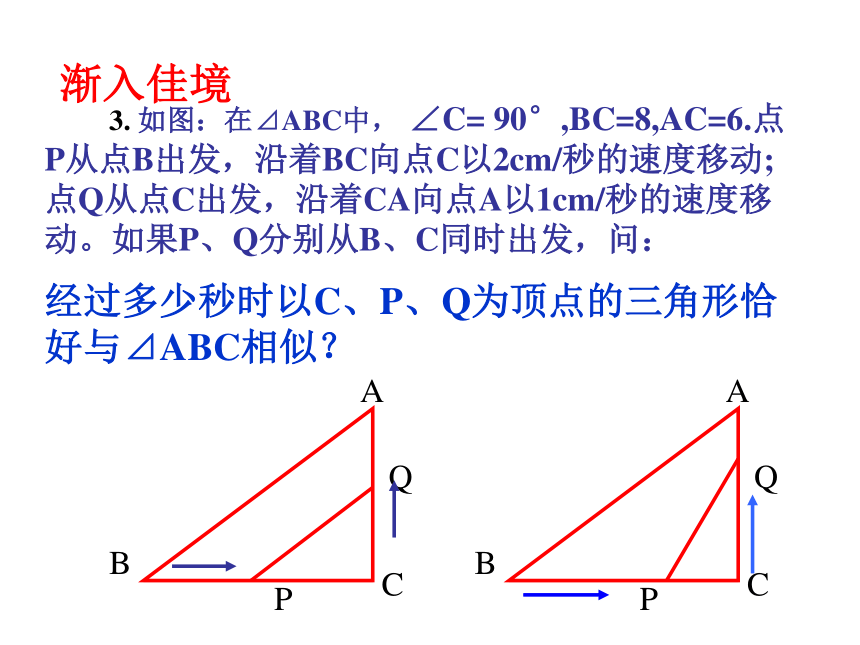
3. 如图：在⊿ABC中， ∠C= 90°,BC=8,AC=6.点P从点B出发，沿着BC向点C以2cm/秒的速度移动;点Q从点C出发，沿着CA向点A以1cm/秒的速度移动。如果P、Q分别从B、C同时出发，问：
A
Q
P
C
B
A
Q
P
C
B
经过多少秒时以C、P、Q为顶点的三角形恰好与⊿ABC相似？
渐入佳境
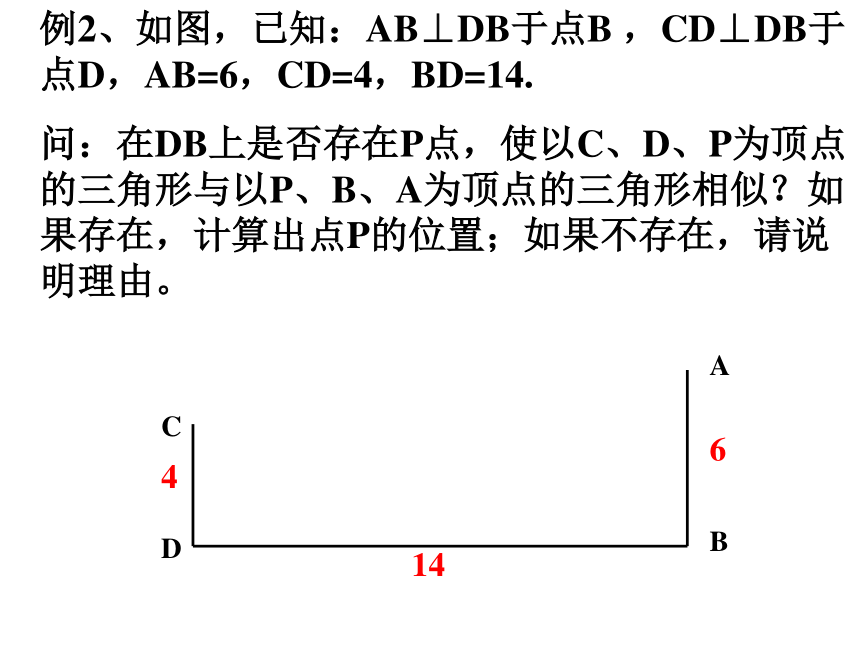
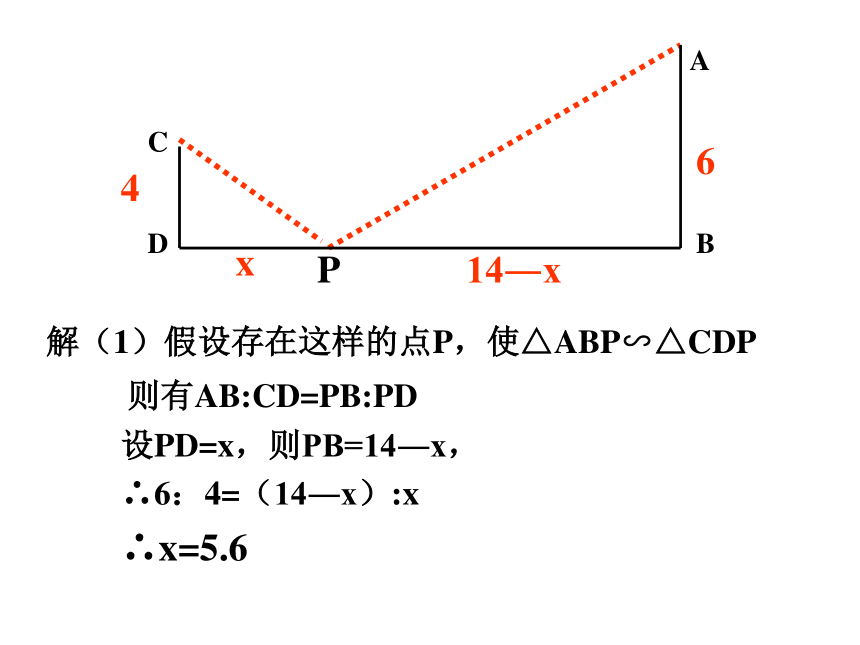
例2、如图，已知：AB⊥DB于点B ，CD⊥DB于点D，AB=6，CD=4，BD=14.
问：在DB上是否存在P点，使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似？如果存在，计算出点P的位置；如果不存在，请说明理由。
4
6
14
A
D
C
B
解（1）假设存在这样的点P，使△ABP∽△CDP
设PD=x，则PB=14―x，
∴6：4=（14―x）:x
则有AB:CD=PB:PD
∴x=5.6
P
6
x
14―x
4
A
D
C
B
P
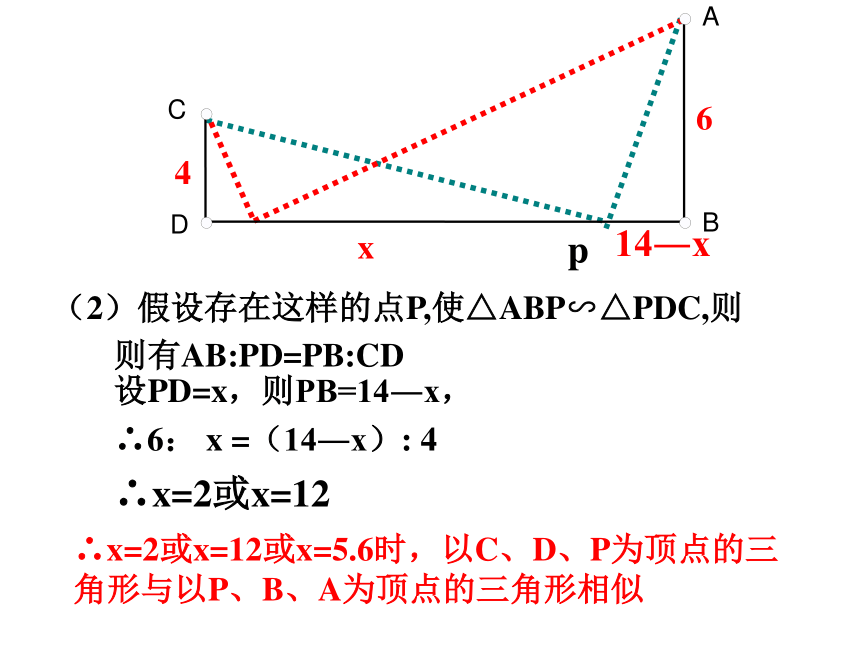
（2）假设存在这样的点P,使△ABP∽△PDC,则
则有AB:PD=PB:CD
设PD=x，则PB=14―x，
∴6： x =（14―x）: 4
∴x=2或x=12
∴x=2或x=12或x=5.6时，以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似
4
6
x
14―x
D
B
C
A
p
已知，D、E为△ABC中BC、AC上两点，
CE=3，CA=8，CB=6， 若∠CDE=∠A，
则：CD=_____，
△CDE的周长:△CAB的周长 = _______,
△CDE的面积:△CAB的面积=______.
E
A
B
C
D
4
1：2
1：4
如图，已知平行四边形ABCD,
CE= BC
S△ADF =16,则S△CEF= ——，平行四边形ABCD的面积为？
A
C
F
E
B
D
如图，在□ABCD中，E为CD上一点，
DE：CE=2：3，连结AE、BE、BD，且
AE、BD交于点F，则S△DEF：S△EBF
：S△ABF=（ ）
（A）4：10：25 （B）4：9：25
（C）2：3：5 （D）2：5：25
F
E
B
A
C
D
A
B
C
D
E
O·
14、如图,⊙O是△ABC的外接圆,AB=AC.
求证:AB2=AE·AD
证明：连接BD
∵AB=AC
∴∠ADB=∠ABE
又∵∠BAD=∠EAB
∴△ABE∽△ADB
∴AB2=AE·AD
=
∴
∴
AD
1.如图，△PCD是等边三角形，A、C、D、B在同
一直线上，且∠APB=120°.
求证：⑴△PAC∽△BPD；⑵AC·BD=CD2.
A
B
C
D
P
(3)如图，在△ABC中，DE∥AB，自D、C、E分
别向AB作垂线，垂足分别为G、H、F， CH交
DE于P，已知 CH=6，AB=8.
①若EF=x ,DE=y，写出y与x的函数关系式.
②设EF为x，S矩形DEFG=S,写出S与x的函数关系式， 以及自变量x的取值范围？
③当x为何值时，矩形DEFG的面积
最大，最大面积为多少？
P
G
H
F
E
A
B
C
D
18、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°
A
B
C
D
E
（1）求证：△ABD∽△DCE
（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出当BD为何值时AE取得最小值
（3）当△ADE是等腰三角形时，求AE的长
1
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°
（1）求证：△ABD∽△DCE
∵∠ADC是△ABD的外角
∴∠ADC=∠ADE+∠2=∠B+∠1
）2
1
证明：∵AB=AC，∠BAC=90°
∴∠B=∠C=45°
又∵∠ADE=45°
∴∠ADE=∠B
∴∠1=∠2
∴ △ABD∽△DCE
A
B
C
D
E
（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出当BD为何值时AE取得最小值
解：∵△ABD∽△DCE
1
∴
∴
∴
当
时
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°
A
B
C
D
E
（3）当△ADE是等腰三角形时，求AE的长
AD=AE
AE=DE
DE=AD
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°
1
A
B
C
D
E
分类讨论
（2）如果点P在AD边上移动（点P与点A、D不重合），且满足∠BPE＝∠A，PE交直线BC于点E，同时交直线DC于点Q，那么
①当点Q在线段DC的延长线上时，设AP＝x，CQ＝y，求y关于x的函数解析式，并写出函
数的定义域；
②当CE＝1时，写出AP的长
已知在梯形ABCD中，AD∥BC，AD＜BC，且AD＝5，AB＝DC＝2．
（1）如图，P为AD上的一点，满足∠BPC＝∠A．
①求证；△ABP∽△DPC ②求AP的长．
2.如图，在△ABC中， CA=6，CB=4，AB=8，
当DE∥AB，D点在BC上（与B、C不重合），
E点在AC上.
(1)当△CED的面积与四边形EABD的面积相等时，求CD的长.
E
A
B
C
D
(2)当△CED的周长与四边形EABD的周长相等时，求CD的长.
E
A
B
C
D
3.在平面直角坐标系，B（1，0）, A（3，－3）, C（3，0）,点P在y轴的正半轴上运动，若以O，B，P为顶点的三角形与△ABC相似，则点P的坐标是__________________.
y
·A
B
C
x
·
·
O
·P
2.画一画:
如图,在△ABC和△DEF中, ∠A=∠D=700, ∠B=500, ∠E=300,画直线a,把△ABC分成两个三角形,画直线b ,把△DEF分成两个三角形,使△ABC分成的两个三角形和△DEF分成的两个三角形分别相似.(要求标注数据)
300
300
C
A
B
700
500
E
D
F
700
300
a
b
C
A
B
700
500
E
D
F
700
300
a
b
200
200
1.如图，△PCD是等边三角形，A、C、D、B在同
一直线上，且∠APB=120°.
求证：⑴△PAC∽△BPD；⑵AC·BD=CD2.
A
B
C
D
P
分析：（1）本题只有已知角和等边三角形的条件，要证∽，可以从找两个角对应相等入手.
（2）欲证 ，只须证 ，但图中找不到能直接得出这个比例式的相似三角形.由于相比的两条线段处在同一直线上，故可考虑通过等量代换，使相比的两条线段不在同一直线上，然后利用第（1）小题结论来解决.
评注：一道题有几个小题时，或者后面小题的解决要用到前面小题的结论，或者这几个小题解决方法类似。本题的第⑴小题也可先证∽，同理可得∽，则有∽。
1.如图，已知△PAC∽△QCB ，
△PCQ是等边三角形
(1)若AP=1，BQ=4，求PQ的长.
(2)求∠ACB的度数.
(3)求证:AC2=AP·AB.
A
B
P
Q
C
板书设计
一、判定方法
平行线法、两角
两角一夹边、三边
相似三角形性质与判定
二、性质
对应边、对应角
周长比、面积比、
对应线段的比
应用2
应用1
已知：如图，D在△ABC的边AC上，且DE∥BC，
交AB于E，F在AE上，且AE2=AF×AB，
求证： △AFD∽ △AEC.
F
E
B
C
A
D