第3章 圆的基本性质 单元测试卷-2021-2022学年浙教版数学九年级上册(Word版 含答案)
文档属性
| 名称 | 第3章 圆的基本性质 单元测试卷-2021-2022学年浙教版数学九年级上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 203.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-26 13:41:10 | ||
图片预览



文档简介
浙教版九年级上册第3章《圆的基本性质》单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是( )
A.点A在圆外
B.点A在圆上
C.点A在圆内
D.不能确定
2.三角形的外接圆的圆心是指三角形什么线的交点( )
A.三边中线
B.三边垂直平分线
C.三边高线
D.三内角的平分线
3.下列说法:(1)直径是弦;
(2)弦是直径;
(3)半圆是弧,但弧不一定是半圆;(4)半径相等的两个圆是等圆;
(5)长度相等的两条弧是等弧.
其中错误的个数是( )
A.1个
B.2个
C.3个
D.4个
4.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是( )
A.152°
B.76°
C.38°
D.14°
5.如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是( )
A.72°
B.108°
C.144°
D.216°
6.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.150°
B.75°
C.60°
D.15°
7.如图,点A,B,C在⊙O上,若∠ACB=112°,则∠α=( )
A.68°
B.112°
C.136°
D.134°
8.如图,点A,B,C,D都在半径为3的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为( )
A.
B.3
C.3
D.2
9.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )
A.3π
B.4π
C.5π
D.6π
10.如图,CD为⊙O直径,CD⊥AB于点F,AE⊥BC于E,AE过圆心O,且AO=1.则四边形BEOF的面积为( )
A.
B.
C.
D.
二.填空题(共6小题,满分24分,每小题4分)
11.已知一个扇形的面积为12πcm2,圆心角的度数为108°,则它的弧长为
.
12.⊙O的圆心是原点O(0,0),半径为5,点A(3,a)在⊙O上,如果点A在第一象限内,那么a=
.
13.如图,在平面直角坐标系中,将点P(4,6)绕坐标原点O顺时针旋转90°得到点Q,则点Q的坐标为
.
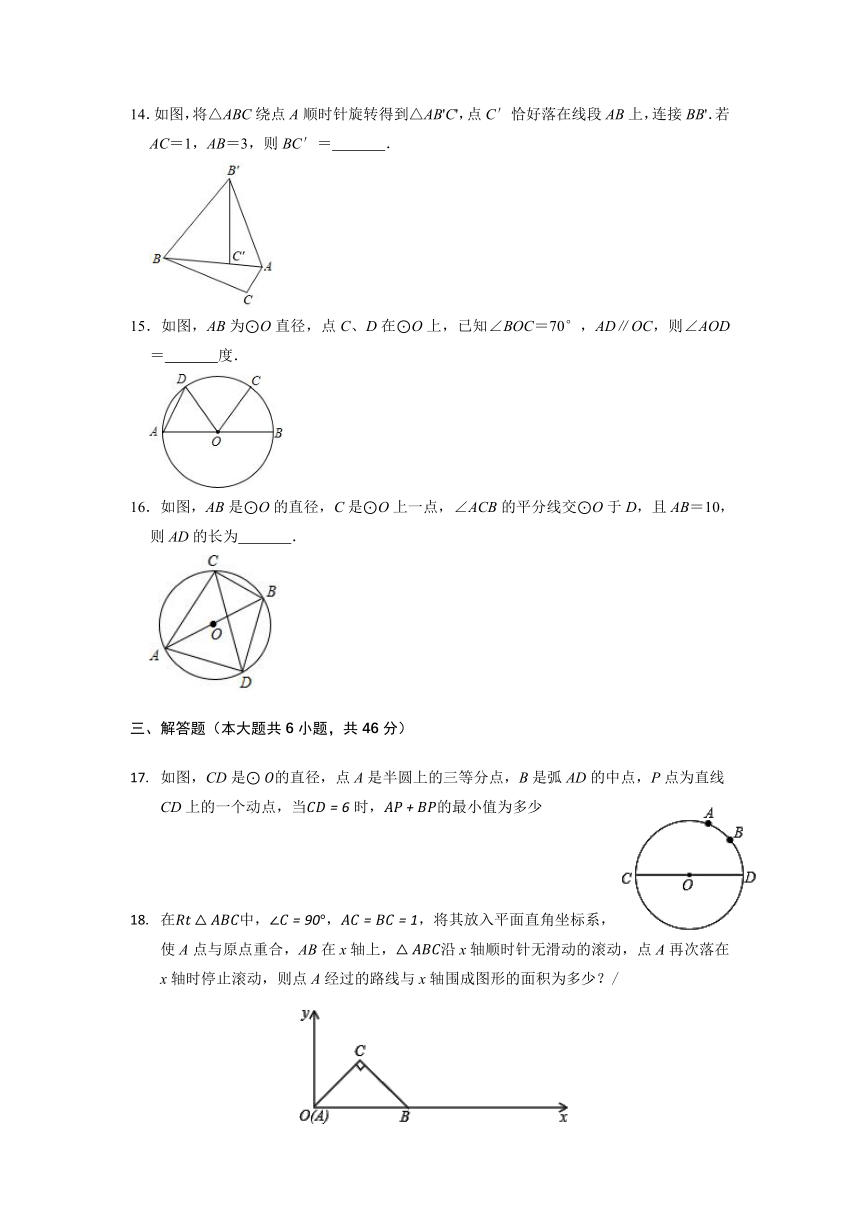
14.如图,将△ABC绕点A顺时针旋转得到△AB'C',点C′恰好落在线段AB上,连接BB'.若AC=1,AB=3,则BC′=
.
15.如图,AB为⊙O直径,点C、D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD=
度.
16.如图,AB是⊙O的直径,C是⊙O上一点,∠ACB的平分线交⊙O于D,且AB=10,则AD的长为
.
三、解答题(本大题共6小题,共46分)
如图,CD是的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当时,的最小值为多少
在中,,,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为多少?/
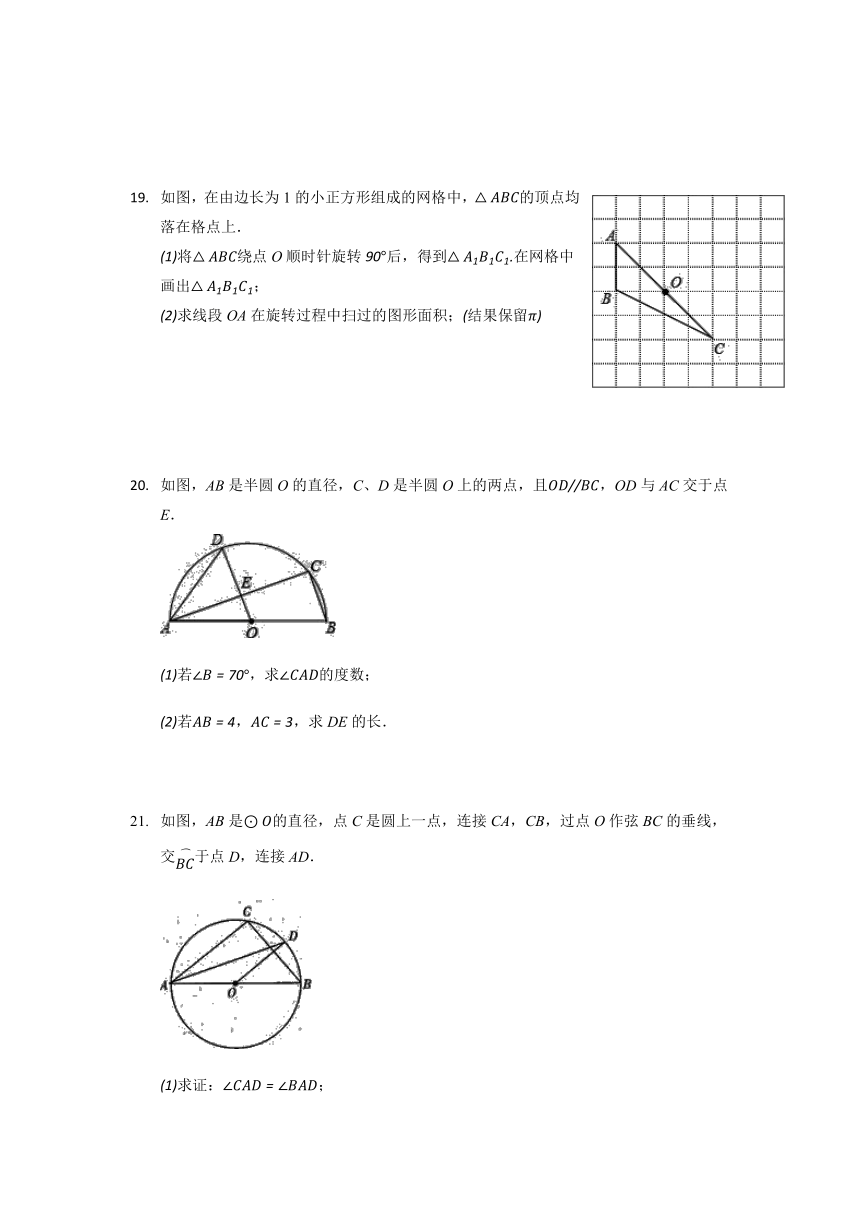
如图,在由边长为1的小正方形组成的网格中,的顶点均落在格点上.
将绕点O顺时针旋转后,得到在网格中画出;
求线段OA在旋转过程中扫过的图形面积;结果保留
如图,AB是半圆O的直径,C、D是半圆O上的两点,且,OD与AC交于点E.
若,求的度数;
若,,求DE的长.
如图,AB是的直径,点C是圆上一点,连接CA,CB,过点O作弦BC的垂线,交于点D,连接AD.
求证:;
若的半径为1,,求的长.
如图,AB是的直径,点C是上一点,连接BC,AC,于E.
求证:;
若,,求的直径.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵⊙O的半径为5cm,点A到圆心O的距离为4cm,
∴d<r,
∴点A与⊙O的位置关系是:点A在圆内,
故选:C.
2.解:根据三角形的外心应到三角形三个顶点的距离相等和线段垂直平分线的性质知,三角形的外心是三角形三边垂直平分线的交点.
故选:B.
3.解:(1)根据弦的概念,直径是一条线段,且两个端点在圆上,满足弦是连接圆上两点的线段这一概念,所以(1)正确;
(2)弦是连接圆上两点的线段,只有过圆心的弦才是直径,其它的弦不是直径,所以(2)错误;
(3)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆.所以(3)正确;
(4)由等圆的定义可知,半径相等的两个圆面积相等、周长相等,所以为等圆,所以(4)正确;
(5)等弧是能完全重合的弧,只有长度相等的两条弧不一定能重合.所以(5)错误.
故选:B.
4.解:∵所对的圆心角是∠BOC,圆周角是∠BAC,
又∵∠BOC=76°,
∴∠A=76°×=38°.
故选:C.
5.解:该图形被平分成五部分,旋转72度的整数倍,就可以与自身重合,因而A、C、D都正确,不能与其自身重合的是B.
故选:B.
6.解:∵在⊙O中,,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选:B.
7.解:作对的圆周角∠ADB,如图,
∵∠ACB+∠ADB=180°,
∴∠ADB=180°﹣112°=68°,
∴∠AOB=2∠ADB=2×68°=136°.
故选:C.
8.解:OA交BC于E,如图,
∵OA⊥BC,
∴=,CE=BE,
∴∠AOB=2∠CDA=2×30°=60°,
在Rt△OBE中,OE=OB=,
∴BE=OE=,
∴BC=2BE=3.
故选:B.
9.解:∵扇形的半径为6,圆心角为120°,
∴此扇形的弧长==4π.
故选:B.
10.解:∵CD为直径,CD⊥AB,
∴=,
∴∠AOD=2∠C,
∵CD⊥AB,AE⊥BC,
∴∠AFO=∠CEO=90°,
在△AFO和△CEO中
∴△AFO≌△CEO(AAS),
∴∠C=∠A,
∴∠AOD=2∠A,
∵∠AFO=90°,
∴∠A=30°,
∵AO=1,
∴OF=AO=,AF=OF=,
同理CE=,OE=,
连接OB,
∵CD⊥AB,AE⊥BC,CD、AE过O,
∴由垂径定理得:BF=AF=,BE=CE=,
∴四边形BEOF的面积S=S△BFO+S△BEO=××+=,
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
11.解:设扇形的半径为Rcm,
∵扇形的面积为12πcm2,圆心角的度数为108°,
∴=12π,
解得:R=2,
∴弧长为=π(cm),
故答案为:πcm.
12.解:∵⊙O的圆心是原点O(0,0),半径为5,点A(3,a)在⊙O上,
∴|a|==4,
∵点A在第一象限内,
∴a=4.
故答案为:4.
13.解:作图如下,
∵∠MPO+∠POM=90°,∠QON+∠POM=90°,
∴∠MPO=∠QON,
在△PMO和△ONQ中,
,
∴△PMO≌△ONQ(AAS),
∴PM=ON,OM=QN,
∵P点坐标为(4,6),
∴Q点坐标为(6,﹣4),
故答案为(6,﹣4).
14.解:∵△ABC绕点A顺时针旋转得到△AB'C',点C′恰好落在线段AB上,
∴AC′=AC=1,
∴BC′=AB﹣AC′=3﹣1=2.
故答案为2.
15.解:∵AD∥OC,
∴∠BOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
16.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ACB的平分线交⊙O于D,
∴∠ACD=∠BCD,
∴=,
∴AD=BD,
∴△ABD为等腰直角三角形,
∴AD=AB=10×=5.
故答案为5.
三.解答题
17.【答案】
解:作点A关于CD的对称点,连接,交CD于点P,此时是最小值,
连接,.
点A与关于CD对称,点A是半圆上的一个三等分点,
,,
点B是弧AD的中点,
,
,
又,
.
.
故答案为:.
18.【答案】
【解析】解:,,
;
根据题意得:绕点B顺时针旋转,BC落在x轴上;再绕点C顺时针旋转,AC落在x轴上,停止滚动;
点A的运动轨迹是:先绕点B旋转,再绕点C旋转;如图所示:
点A经过的路线与x轴围成的图形是:
一个圆心角为,半径为的扇形,加上,再加上圆心角是,半径是1的扇形;
点A经过的路线与x轴围成图形的面积
.
故答案为:.
由勾股定理求出AB,由题意得出点A经过的路线与x轴围成的图形是一个圆心角为,半径为的扇形,加上,再加上圆心角是,半径是1的扇形;由扇形的面积和三角形的面积公式即可得出结果.
本题考查了旋转的性质、扇形面积的计算公式;根据题意得出点A经过的路线与x轴围成的图形由三部分组成是解决问题的关键.
19.【答案】解:如图.
即为所求三角形;
由勾股定理可知,
线段OA在旋转过程中扫过的图形为以OA为半径,为圆心角的扇形,
则.
答:扫过的图形面积为.
20.【答案】解:是半圆O的直径,
,
又,
,即,
,.
,
,
;
在直角中,
.
,
,
又,
.
又,
.
21.【答案】解:证明:是圆心,,
弧弧BD,
;
连接CO,
,
,
弧AC的长:.
22.【答案】证明:是的直径,,
,,
;
解:令的半径为r,则
?
?
?
根据垂径定理可得:,
在中
由勾股定理得:,
解得:,
所以的直径为.
一.选择题(共10小题,满分30分,每小题3分)
1.若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是( )
A.点A在圆外
B.点A在圆上
C.点A在圆内
D.不能确定
2.三角形的外接圆的圆心是指三角形什么线的交点( )
A.三边中线
B.三边垂直平分线
C.三边高线
D.三内角的平分线
3.下列说法:(1)直径是弦;
(2)弦是直径;
(3)半圆是弧,但弧不一定是半圆;(4)半径相等的两个圆是等圆;
(5)长度相等的两条弧是等弧.
其中错误的个数是( )
A.1个
B.2个
C.3个
D.4个
4.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC的度数是( )
A.152°
B.76°
C.38°
D.14°
5.如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是( )
A.72°
B.108°
C.144°
D.216°
6.如图所示,在⊙O中,,∠A=30°,则∠B=( )
A.150°
B.75°
C.60°
D.15°
7.如图,点A,B,C在⊙O上,若∠ACB=112°,则∠α=( )
A.68°
B.112°
C.136°
D.134°
8.如图,点A,B,C,D都在半径为3的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为( )
A.
B.3
C.3
D.2
9.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )
A.3π
B.4π
C.5π
D.6π
10.如图,CD为⊙O直径,CD⊥AB于点F,AE⊥BC于E,AE过圆心O,且AO=1.则四边形BEOF的面积为( )
A.
B.
C.
D.
二.填空题(共6小题,满分24分,每小题4分)
11.已知一个扇形的面积为12πcm2,圆心角的度数为108°,则它的弧长为
.
12.⊙O的圆心是原点O(0,0),半径为5,点A(3,a)在⊙O上,如果点A在第一象限内,那么a=
.
13.如图,在平面直角坐标系中,将点P(4,6)绕坐标原点O顺时针旋转90°得到点Q,则点Q的坐标为
.
14.如图,将△ABC绕点A顺时针旋转得到△AB'C',点C′恰好落在线段AB上,连接BB'.若AC=1,AB=3,则BC′=
.
15.如图,AB为⊙O直径,点C、D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD=
度.
16.如图,AB是⊙O的直径,C是⊙O上一点,∠ACB的平分线交⊙O于D,且AB=10,则AD的长为
.
三、解答题(本大题共6小题,共46分)
如图,CD是的直径,点A是半圆上的三等分点,B是弧AD的中点,P点为直线CD上的一个动点,当时,的最小值为多少
在中,,,将其放入平面直角坐标系,使A点与原点重合,AB在x轴上,沿x轴顺时针无滑动的滚动,点A再次落在x轴时停止滚动,则点A经过的路线与x轴围成图形的面积为多少?/
如图,在由边长为1的小正方形组成的网格中,的顶点均落在格点上.
将绕点O顺时针旋转后,得到在网格中画出;
求线段OA在旋转过程中扫过的图形面积;结果保留
如图,AB是半圆O的直径,C、D是半圆O上的两点,且,OD与AC交于点E.
若,求的度数;
若,,求DE的长.
如图,AB是的直径,点C是圆上一点,连接CA,CB,过点O作弦BC的垂线,交于点D,连接AD.
求证:;
若的半径为1,,求的长.
如图,AB是的直径,点C是上一点,连接BC,AC,于E.
求证:;
若,,求的直径.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:∵⊙O的半径为5cm,点A到圆心O的距离为4cm,
∴d<r,
∴点A与⊙O的位置关系是:点A在圆内,
故选:C.
2.解:根据三角形的外心应到三角形三个顶点的距离相等和线段垂直平分线的性质知,三角形的外心是三角形三边垂直平分线的交点.
故选:B.
3.解:(1)根据弦的概念,直径是一条线段,且两个端点在圆上,满足弦是连接圆上两点的线段这一概念,所以(1)正确;
(2)弦是连接圆上两点的线段,只有过圆心的弦才是直径,其它的弦不是直径,所以(2)错误;
(3)圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆.所以(3)正确;
(4)由等圆的定义可知,半径相等的两个圆面积相等、周长相等,所以为等圆,所以(4)正确;
(5)等弧是能完全重合的弧,只有长度相等的两条弧不一定能重合.所以(5)错误.
故选:B.
4.解:∵所对的圆心角是∠BOC,圆周角是∠BAC,
又∵∠BOC=76°,
∴∠A=76°×=38°.
故选:C.
5.解:该图形被平分成五部分,旋转72度的整数倍,就可以与自身重合,因而A、C、D都正确,不能与其自身重合的是B.
故选:B.
6.解:∵在⊙O中,,
∴AB=AC,
∴△ABC是等腰三角形,
∴∠B=∠C;
又∠A=30°,
∴∠B==75°(三角形内角和定理).
故选:B.
7.解:作对的圆周角∠ADB,如图,
∵∠ACB+∠ADB=180°,
∴∠ADB=180°﹣112°=68°,
∴∠AOB=2∠ADB=2×68°=136°.
故选:C.
8.解:OA交BC于E,如图,
∵OA⊥BC,
∴=,CE=BE,
∴∠AOB=2∠CDA=2×30°=60°,
在Rt△OBE中,OE=OB=,
∴BE=OE=,
∴BC=2BE=3.
故选:B.
9.解:∵扇形的半径为6,圆心角为120°,
∴此扇形的弧长==4π.
故选:B.
10.解:∵CD为直径,CD⊥AB,
∴=,
∴∠AOD=2∠C,
∵CD⊥AB,AE⊥BC,
∴∠AFO=∠CEO=90°,
在△AFO和△CEO中
∴△AFO≌△CEO(AAS),
∴∠C=∠A,
∴∠AOD=2∠A,
∵∠AFO=90°,
∴∠A=30°,
∵AO=1,
∴OF=AO=,AF=OF=,
同理CE=,OE=,
连接OB,
∵CD⊥AB,AE⊥BC,CD、AE过O,
∴由垂径定理得:BF=AF=,BE=CE=,
∴四边形BEOF的面积S=S△BFO+S△BEO=××+=,
故选:C.
二.填空题(共6小题,满分24分,每小题4分)
11.解:设扇形的半径为Rcm,
∵扇形的面积为12πcm2,圆心角的度数为108°,
∴=12π,
解得:R=2,
∴弧长为=π(cm),
故答案为:πcm.
12.解:∵⊙O的圆心是原点O(0,0),半径为5,点A(3,a)在⊙O上,
∴|a|==4,
∵点A在第一象限内,
∴a=4.
故答案为:4.
13.解:作图如下,
∵∠MPO+∠POM=90°,∠QON+∠POM=90°,
∴∠MPO=∠QON,
在△PMO和△ONQ中,
,
∴△PMO≌△ONQ(AAS),
∴PM=ON,OM=QN,
∵P点坐标为(4,6),
∴Q点坐标为(6,﹣4),
故答案为(6,﹣4).
14.解:∵△ABC绕点A顺时针旋转得到△AB'C',点C′恰好落在线段AB上,
∴AC′=AC=1,
∴BC′=AB﹣AC′=3﹣1=2.
故答案为2.
15.解:∵AD∥OC,
∴∠BOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
16.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ACB的平分线交⊙O于D,
∴∠ACD=∠BCD,
∴=,
∴AD=BD,
∴△ABD为等腰直角三角形,
∴AD=AB=10×=5.
故答案为5.
三.解答题
17.【答案】
解:作点A关于CD的对称点,连接,交CD于点P,此时是最小值,
连接,.
点A与关于CD对称,点A是半圆上的一个三等分点,
,,
点B是弧AD的中点,
,
,
又,
.
.
故答案为:.
18.【答案】
【解析】解:,,
;
根据题意得:绕点B顺时针旋转,BC落在x轴上;再绕点C顺时针旋转,AC落在x轴上,停止滚动;
点A的运动轨迹是:先绕点B旋转,再绕点C旋转;如图所示:
点A经过的路线与x轴围成的图形是:
一个圆心角为,半径为的扇形,加上,再加上圆心角是,半径是1的扇形;
点A经过的路线与x轴围成图形的面积
.
故答案为:.
由勾股定理求出AB,由题意得出点A经过的路线与x轴围成的图形是一个圆心角为,半径为的扇形,加上,再加上圆心角是,半径是1的扇形;由扇形的面积和三角形的面积公式即可得出结果.
本题考查了旋转的性质、扇形面积的计算公式;根据题意得出点A经过的路线与x轴围成的图形由三部分组成是解决问题的关键.
19.【答案】解:如图.
即为所求三角形;
由勾股定理可知,
线段OA在旋转过程中扫过的图形为以OA为半径,为圆心角的扇形,
则.
答:扫过的图形面积为.
20.【答案】解:是半圆O的直径,
,
又,
,即,
,.
,
,
;
在直角中,
.
,
,
又,
.
又,
.
21.【答案】解:证明:是圆心,,
弧弧BD,
;
连接CO,
,
,
弧AC的长:.
22.【答案】证明:是的直径,,
,,
;
解:令的半径为r,则
?
?
?
根据垂径定理可得:,
在中
由勾股定理得:,
解得:,
所以的直径为.
同课章节目录
