2.1有理数的加法 同步练习2021-2022学年浙教版数学七年级上册(Word版含答案)
文档属性
| 名称 | 2.1有理数的加法 同步练习2021-2022学年浙教版数学七年级上册(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 14:31:00 | ||
图片预览

文档简介
有理数的加法
一、单选题
1.计算的结果是(
)
A.
B.
C.2
D.15
2.贵阳市元月份某一天早晨的气温是-3℃,中午上升了2℃,则中午的气温是(
)
A.-5℃
B.5℃
C.-1℃
D.1℃
3.数轴上点表示的数是-2,将点在数轴上向右平移5个单位长度得到点,则点表示的数是(
)
A.-7
B.7
C.-3
D.3
4.绝对值小于4的所有整数之和为(
)
A.3
B.6
C.0
D.2
5.已知,那么的大小关系是(
)
A.
B.
C.
D.
6.我国是最早认识负数,并进行相关运算的国家在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算的过程按照这种方法,图2表示的过程应是在计算(
)
A.
B.
C.
D.
7.比﹣2大2的数是( )
A.4
B.0
C.﹣2
D.﹣4
8.记运入仓库的大米吨数为正,则表示(
)
A.先运入大米3.5吨,后运入大米2.5吨
B.先运出大米3.5吨,后运入大米2.5吨
C.先运入大米3.5吨,后运出大米2.5吨
D.先运出大米3.5吨,后运出大米2.5吨
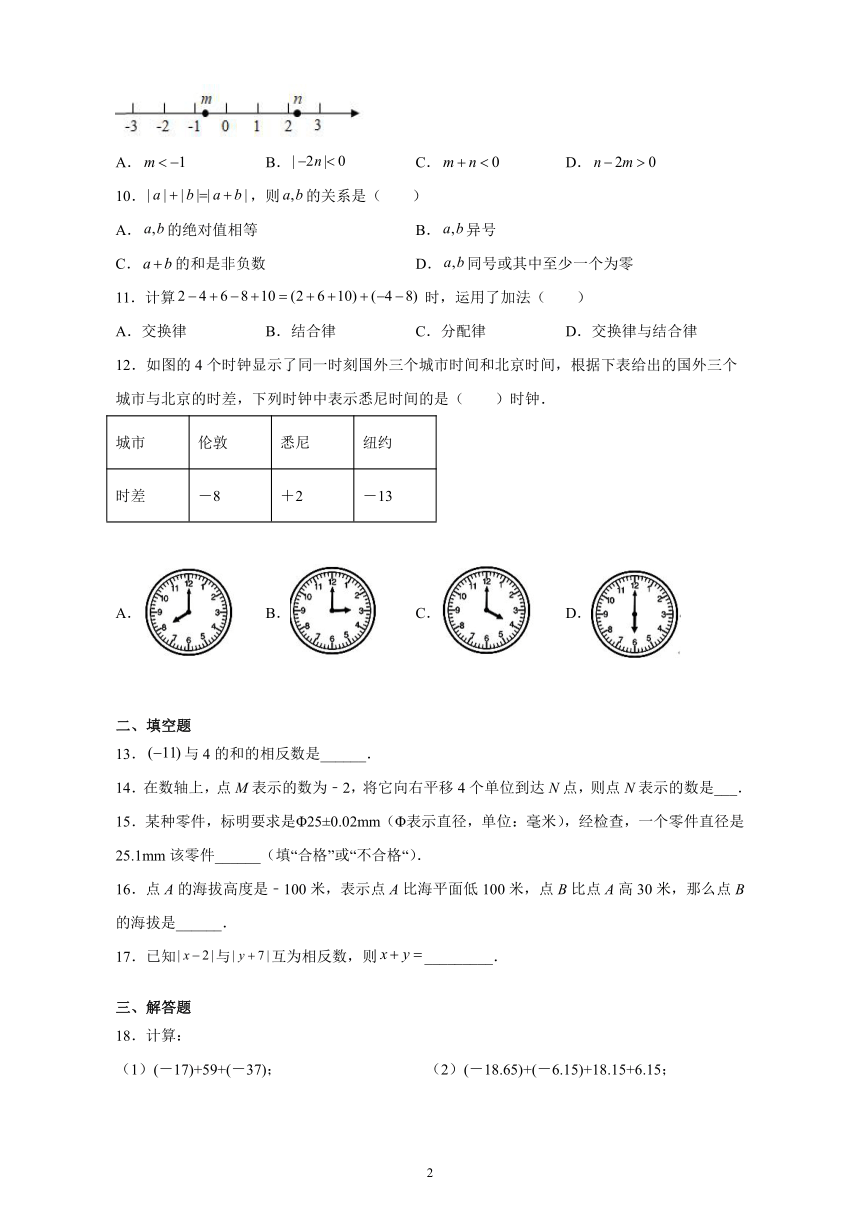
9.实数在数轴上的对应点的位置如图所示,则正确的结论是(
)
A.
B.
C.
D.
10.,则的关系是(
)
A.的绝对值相等
B.异号
C.的和是非负数
D.同号或其中至少一个为零
11.计算时,运用了加法(
)
A.交换律
B.结合律
C.分配律
D.交换律与结合律
12.如图的4个时钟显示了同一时刻国外三个城市时间和北京时间,根据下表给出的国外三个城市与北京的时差,下列时钟中表示悉尼时间的是(
)时钟.
城市
伦敦
悉尼
纽约
时差
-8
+2
-13
A.
B.
C.
D.
二、填空题
13.与4的和的相反数是______.
14.在数轴上,点M表示的数为﹣2,将它向右平移4个单位到达N点,则点N表示的数是___.
15.某种零件,标明要求是Φ25±0.02mm(Φ表示直径,单位:毫米),经检查,一个零件直径是25.1mm该零件______(填“合格”或“不合格“).
16.点A的海拔高度是﹣100米,表示点A比海平面低100米,点B比点A高30米,那么点B的海拔是______.
17.已知与互为相反数,则_________.
三、解答题
18.计算:
(1)(-17)+59+(-37);
(2)(-18.65)+(-6.15)+18.15+6.15;
(3)(-4)+(-3)+6+(-2);
(4)(-0.5)+3+2.75+(-5)
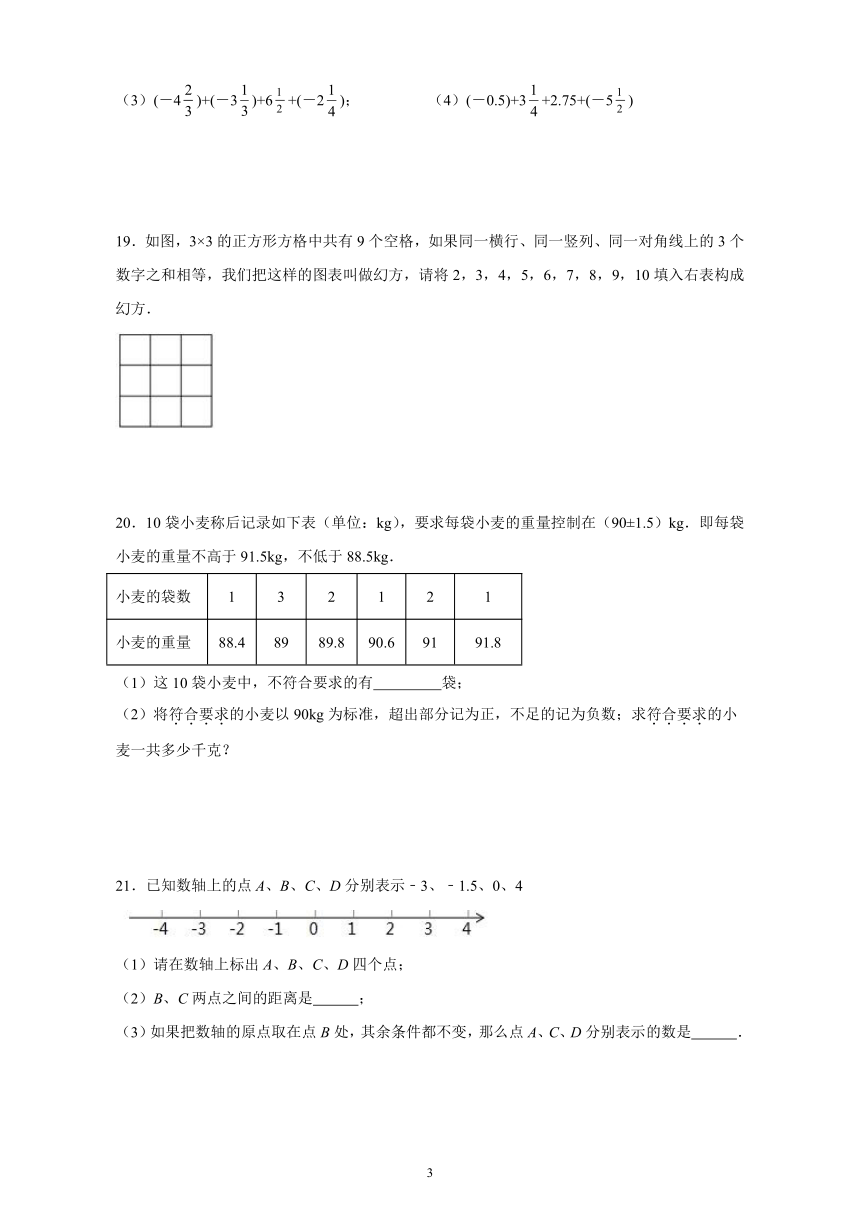
19.如图,3×3的正方形方格中共有9个空格,如果同一横行、同一竖列、同一对角线上的3个数字之和相等,我们把这样的图表叫做幻方,请将2,3,4,5,6,7,8,9,10填入右表构成幻方.
20.10袋小麦称后记录如下表(单位:kg),要求每袋小麦的重量控制在(90±1.5)kg.即每袋小麦的重量不高于91.5kg,不低于88.5kg.
小麦的袋数
1
3
2
1
2
1
小麦的重量
88.4
89
89.8
90.6
91
91.8
(1)这10袋小麦中,不符合要求的有
袋;
(2)将符合要求的小麦以90kg为标准,超出部分记为正,不足的记为负数;求符合要求的小麦一共多少千克?
21.已知数轴上的点A、B、C、D分别表示﹣3、﹣1.5、0、4
(1)请在数轴上标出A、B、C、D四个点;
(2)B、C两点之间的距离是
;
(3)如果把数轴的原点取在点B处,其余条件都不变,那么点A、C、D分别表示的数是
.
参考答案
1.B
解:=-2,
故选:B.
2.C
解:-3+2=-1(℃)
∴中午的气温是-1℃.
故选:C.
3.D
解:由题意得:点表示的数是,
故选:D.
4.C
解:∵绝对值小于4的所有整数是?3,?2,?1,0,1,2,3,
∴其和为:3+2+1+0?3?2?1=0.
故选:C.
5.D
解:∵b<0,a+b>0,
∴a>-b>0,-a<0,
∴-a<b<0,
∴a,b,-a,-b的大小关系为a>-b>b>-a.
故选:D.
6.D
解:由图1知:白色表示正数,黑色表示负数,
所以图2表示的过程应是在计算5+(?2),
故选:D.
7.B
解:由题意得:-2+2=0;
故选B.
8.C
解:∵运入仓库的大米吨数为正,
则运出仓库的大米吨数为负,
∴表示:先运入大米3.5吨,后运出大米2.5吨,
故选:C.
9.D
解:由数轴可得,
?1<m<0<2<n<3,故选项A错误,选项B错误,
∴m>?n,即:,故选项C错误,
∵,故选项D正确,
故选:D.
10.D
解:∵|a+b|=|a|+|b|,
∴a、b满足的关系是a、b同号或a、b有一个为0,或同时为0,
故选:D.
11.D
解:0
=(加法交换律)
=
(加法结合律)
故选:D.
12.D
解:若第一个时钟表示北京时间,则伦敦时间应该是12点,剩下三个时钟里没有12点,故第一个时钟不是北京时间;
若第二个时钟表示北京时间,则伦敦时间应该是7点,剩下三个时钟里没有7点,故第二个时钟不是北京时间;
若第三个时钟表示北京时间,则伦敦时间应该是8点,对应第一个时钟;悉尼时间应该是6点,对应第四个时钟;纽约时间应该是3点,对应第二个时钟,符合题意;
若第四个时钟表示北京时间,则伦敦时间应该是10点,剩下三个时钟里没有10点,故第四
个时钟不是北京时间.
综上所述,表示悉尼时间的是第四个时钟.
故选:D
.
13.7
解:略
14.2
解:﹣2+4=2,
故答案为:2.
15.不合格
解:∵零件,标明要求是Φ25±0.02mm,即24.98mm≤Φ≤25.02mm,
∴直径是25.1mm的零件不合格,
故答案为:不合格
16.米
解:由题意得:点的海拔高度为(米),
故答案为:米.
17.-5
解:∵|x-2|与|y+7|互为相反数,
∴|x-2|+|y+7|=0,
∴x-2=0,y+7=0,
∴x=2,y=-7
∴x+y=2-7=-5,
故答案为:-5.
18.(1)5;(2)-0.5;(3);(4)0
解:(1)(-17)+59+(-37)
(2)(-18.65)+(-6.15)+18.15+6.15
=[(-17)+(-37)]+59
=[(-6.15)+6.15]+[(-18.65)+18.15]
=(-54)+59
=0+(-0.5)
=5
=-0.5
(3)(-4)+(-3)+6+(-2)
(4)(-0.5)+3+2.75+(-5)
=[(-4)+(-3)+(-2)]+6
=[(-0.5)+(-5)]+(3+2.75)
=(-10)+6
=-6+6
=-3
=0
19.见解析
解:如表:
5
10
3
4
6
8
9
2
7
解:(1)这10袋小麦中,不符合要求的有2袋;
故答案为:2;
(2)将符合要求的小麦以90kg为标准,超出部分记为正,不足的记为负如下,
-1.6,-1,-0,2,+0.6,+1,+0.8,;
符合要求的小麦一共有:89×3+89.8×2+90.6+91×2=719.2千克.
21.(1)见解析;(2)1.5;(3)﹣1.5,0,1.5,5.5
解:(1)如图所示:
(2)B、C两点的距离=0﹣(﹣1.5)=1.5;
(3)点A表示的数为:﹣3+1.5=﹣1.5,点B表示的数为0,点C表示的数为0+1.5=1.5,点D表示的数为4+1.5=5.5.
故答案为:1.5;﹣1.5,0,1.5,5.5.
一、单选题
1.计算的结果是(
)
A.
B.
C.2
D.15
2.贵阳市元月份某一天早晨的气温是-3℃,中午上升了2℃,则中午的气温是(
)
A.-5℃
B.5℃
C.-1℃
D.1℃
3.数轴上点表示的数是-2,将点在数轴上向右平移5个单位长度得到点,则点表示的数是(
)
A.-7
B.7
C.-3
D.3
4.绝对值小于4的所有整数之和为(
)
A.3
B.6
C.0
D.2
5.已知,那么的大小关系是(
)
A.
B.
C.
D.
6.我国是最早认识负数,并进行相关运算的国家在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算的过程按照这种方法,图2表示的过程应是在计算(
)
A.
B.
C.
D.
7.比﹣2大2的数是( )
A.4
B.0
C.﹣2
D.﹣4
8.记运入仓库的大米吨数为正,则表示(
)
A.先运入大米3.5吨,后运入大米2.5吨
B.先运出大米3.5吨,后运入大米2.5吨
C.先运入大米3.5吨,后运出大米2.5吨
D.先运出大米3.5吨,后运出大米2.5吨
9.实数在数轴上的对应点的位置如图所示,则正确的结论是(
)
A.
B.
C.
D.
10.,则的关系是(
)
A.的绝对值相等
B.异号
C.的和是非负数
D.同号或其中至少一个为零
11.计算时,运用了加法(
)
A.交换律
B.结合律
C.分配律
D.交换律与结合律
12.如图的4个时钟显示了同一时刻国外三个城市时间和北京时间,根据下表给出的国外三个城市与北京的时差,下列时钟中表示悉尼时间的是(
)时钟.
城市
伦敦
悉尼
纽约
时差
-8
+2
-13
A.
B.
C.
D.
二、填空题
13.与4的和的相反数是______.
14.在数轴上,点M表示的数为﹣2,将它向右平移4个单位到达N点,则点N表示的数是___.
15.某种零件,标明要求是Φ25±0.02mm(Φ表示直径,单位:毫米),经检查,一个零件直径是25.1mm该零件______(填“合格”或“不合格“).
16.点A的海拔高度是﹣100米,表示点A比海平面低100米,点B比点A高30米,那么点B的海拔是______.
17.已知与互为相反数,则_________.
三、解答题
18.计算:
(1)(-17)+59+(-37);
(2)(-18.65)+(-6.15)+18.15+6.15;
(3)(-4)+(-3)+6+(-2);
(4)(-0.5)+3+2.75+(-5)
19.如图,3×3的正方形方格中共有9个空格,如果同一横行、同一竖列、同一对角线上的3个数字之和相等,我们把这样的图表叫做幻方,请将2,3,4,5,6,7,8,9,10填入右表构成幻方.
20.10袋小麦称后记录如下表(单位:kg),要求每袋小麦的重量控制在(90±1.5)kg.即每袋小麦的重量不高于91.5kg,不低于88.5kg.
小麦的袋数
1
3
2
1
2
1
小麦的重量
88.4
89
89.8
90.6
91
91.8
(1)这10袋小麦中,不符合要求的有
袋;
(2)将符合要求的小麦以90kg为标准,超出部分记为正,不足的记为负数;求符合要求的小麦一共多少千克?
21.已知数轴上的点A、B、C、D分别表示﹣3、﹣1.5、0、4
(1)请在数轴上标出A、B、C、D四个点;
(2)B、C两点之间的距离是
;
(3)如果把数轴的原点取在点B处,其余条件都不变,那么点A、C、D分别表示的数是
.
参考答案
1.B
解:=-2,
故选:B.
2.C
解:-3+2=-1(℃)
∴中午的气温是-1℃.
故选:C.
3.D
解:由题意得:点表示的数是,
故选:D.
4.C
解:∵绝对值小于4的所有整数是?3,?2,?1,0,1,2,3,
∴其和为:3+2+1+0?3?2?1=0.
故选:C.
5.D
解:∵b<0,a+b>0,
∴a>-b>0,-a<0,
∴-a<b<0,
∴a,b,-a,-b的大小关系为a>-b>b>-a.
故选:D.
6.D
解:由图1知:白色表示正数,黑色表示负数,
所以图2表示的过程应是在计算5+(?2),
故选:D.
7.B
解:由题意得:-2+2=0;
故选B.
8.C
解:∵运入仓库的大米吨数为正,
则运出仓库的大米吨数为负,
∴表示:先运入大米3.5吨,后运出大米2.5吨,
故选:C.
9.D
解:由数轴可得,
?1<m<0<2<n<3,故选项A错误,选项B错误,
∴m>?n,即:,故选项C错误,
∵,故选项D正确,
故选:D.
10.D
解:∵|a+b|=|a|+|b|,
∴a、b满足的关系是a、b同号或a、b有一个为0,或同时为0,
故选:D.
11.D
解:0
=(加法交换律)
=
(加法结合律)
故选:D.
12.D
解:若第一个时钟表示北京时间,则伦敦时间应该是12点,剩下三个时钟里没有12点,故第一个时钟不是北京时间;
若第二个时钟表示北京时间,则伦敦时间应该是7点,剩下三个时钟里没有7点,故第二个时钟不是北京时间;
若第三个时钟表示北京时间,则伦敦时间应该是8点,对应第一个时钟;悉尼时间应该是6点,对应第四个时钟;纽约时间应该是3点,对应第二个时钟,符合题意;
若第四个时钟表示北京时间,则伦敦时间应该是10点,剩下三个时钟里没有10点,故第四
个时钟不是北京时间.
综上所述,表示悉尼时间的是第四个时钟.
故选:D
.
13.7
解:略
14.2
解:﹣2+4=2,
故答案为:2.
15.不合格
解:∵零件,标明要求是Φ25±0.02mm,即24.98mm≤Φ≤25.02mm,
∴直径是25.1mm的零件不合格,
故答案为:不合格
16.米
解:由题意得:点的海拔高度为(米),
故答案为:米.
17.-5
解:∵|x-2|与|y+7|互为相反数,
∴|x-2|+|y+7|=0,
∴x-2=0,y+7=0,
∴x=2,y=-7
∴x+y=2-7=-5,
故答案为:-5.
18.(1)5;(2)-0.5;(3);(4)0
解:(1)(-17)+59+(-37)
(2)(-18.65)+(-6.15)+18.15+6.15
=[(-17)+(-37)]+59
=[(-6.15)+6.15]+[(-18.65)+18.15]
=(-54)+59
=0+(-0.5)
=5
=-0.5
(3)(-4)+(-3)+6+(-2)
(4)(-0.5)+3+2.75+(-5)
=[(-4)+(-3)+(-2)]+6
=[(-0.5)+(-5)]+(3+2.75)
=(-10)+6
=-6+6
=-3
=0
19.见解析
解:如表:
5
10
3
4
6
8
9
2
7
解:(1)这10袋小麦中,不符合要求的有2袋;
故答案为:2;
(2)将符合要求的小麦以90kg为标准,超出部分记为正,不足的记为负如下,
-1.6,-1,-0,2,+0.6,+1,+0.8,;
符合要求的小麦一共有:89×3+89.8×2+90.6+91×2=719.2千克.
21.(1)见解析;(2)1.5;(3)﹣1.5,0,1.5,5.5
解:(1)如图所示:
(2)B、C两点的距离=0﹣(﹣1.5)=1.5;
(3)点A表示的数为:﹣3+1.5=﹣1.5,点B表示的数为0,点C表示的数为0+1.5=1.5,点D表示的数为4+1.5=5.5.
故答案为:1.5;﹣1.5,0,1.5,5.5.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
