第 1章三角形的初步认识单元测试卷-2021-2022学年浙教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 第 1章三角形的初步认识单元测试卷-2021-2022学年浙教版八年级数学上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 221.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 14:50:33 | ||
图片预览


文档简介
浙教新版八年级数学上册第
1章三角形的初步认识单元测试卷
一、选择题
1.在一个三角形的三个外角中,钝角的个数最多有(
)
A.3个
B.2个
C.1个
D.0个
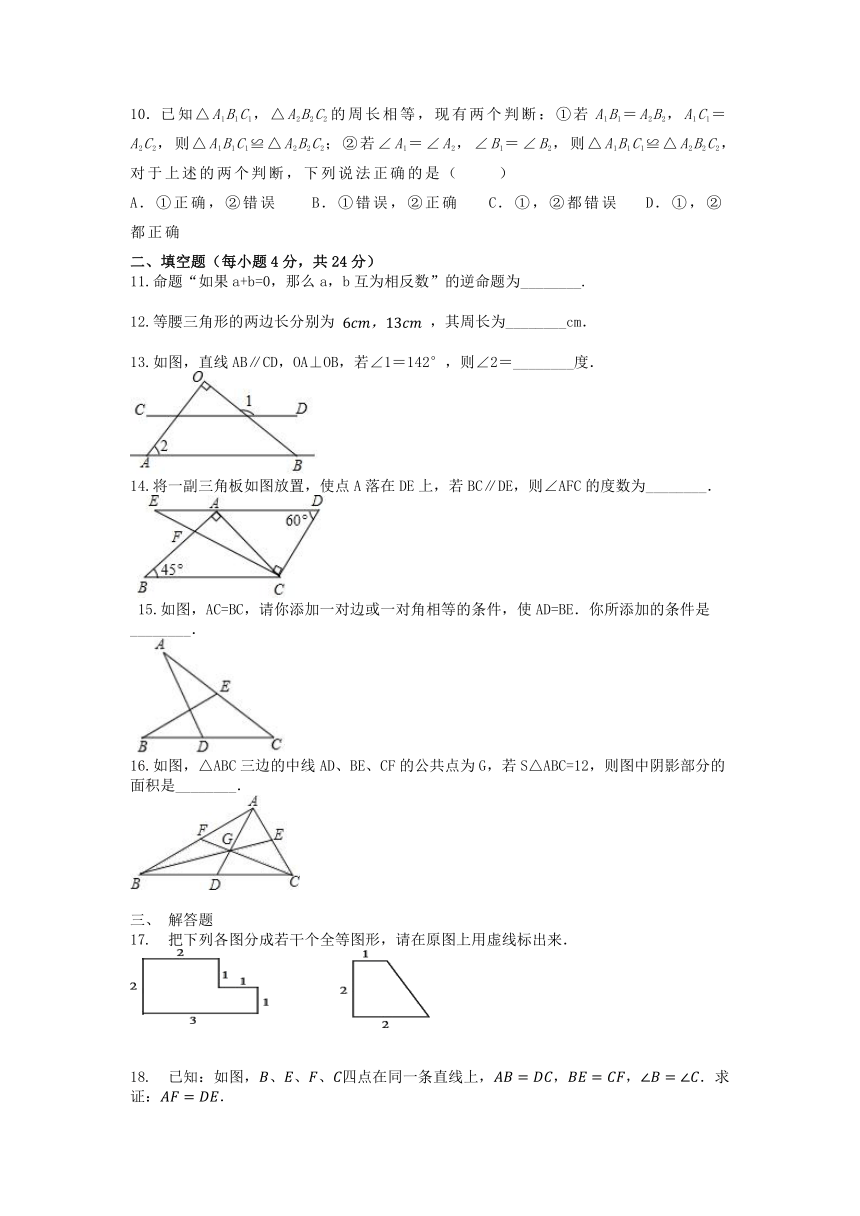
2.如图,D在AB上,E在AC上,且∠B=∠C,则再添加下列条件,仍无法判定△ABE≌△ACD的是(
)
A.AD=AE
B.AB=AC
C.BE=CD
D.∠AEB=∠ADC
3.已知三角形的两边分别为1和4,第三边长为整数
,则该三角形的周长为(
?
)
A.?7?
????B.?8???????
?C.?9??????
?D.?10
4.尺规作图作的平分线方法如下:如图,以点O为圆心,任意长为半径画弧分别交OA,OB于点C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP,由作法得的根据是(
)
A.
SAS
B.
ASA
C.
AAS
D.
SSS
5.如图,AD是的中线,点E,F分别在AB,AC上(点E,F不与端点重合),且.则线段BE,CF,EF的关系是(
)
A.
B.
C.
D.
与EF的大小关系不确定
6.如图△ABC,AC=BC,∠ACB=90°,AD为角平分线,延长AD交BF于E,E为BF中点,下列结论错误的是(?
?
)
A.?AD=BF???
?B.?CF=CD????
?
C.?AC+CD=AB???
?D.?BE=CF
7.
如图,
AD是的中线,E,F分别是AD和AD延长线上的点,且,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;
③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
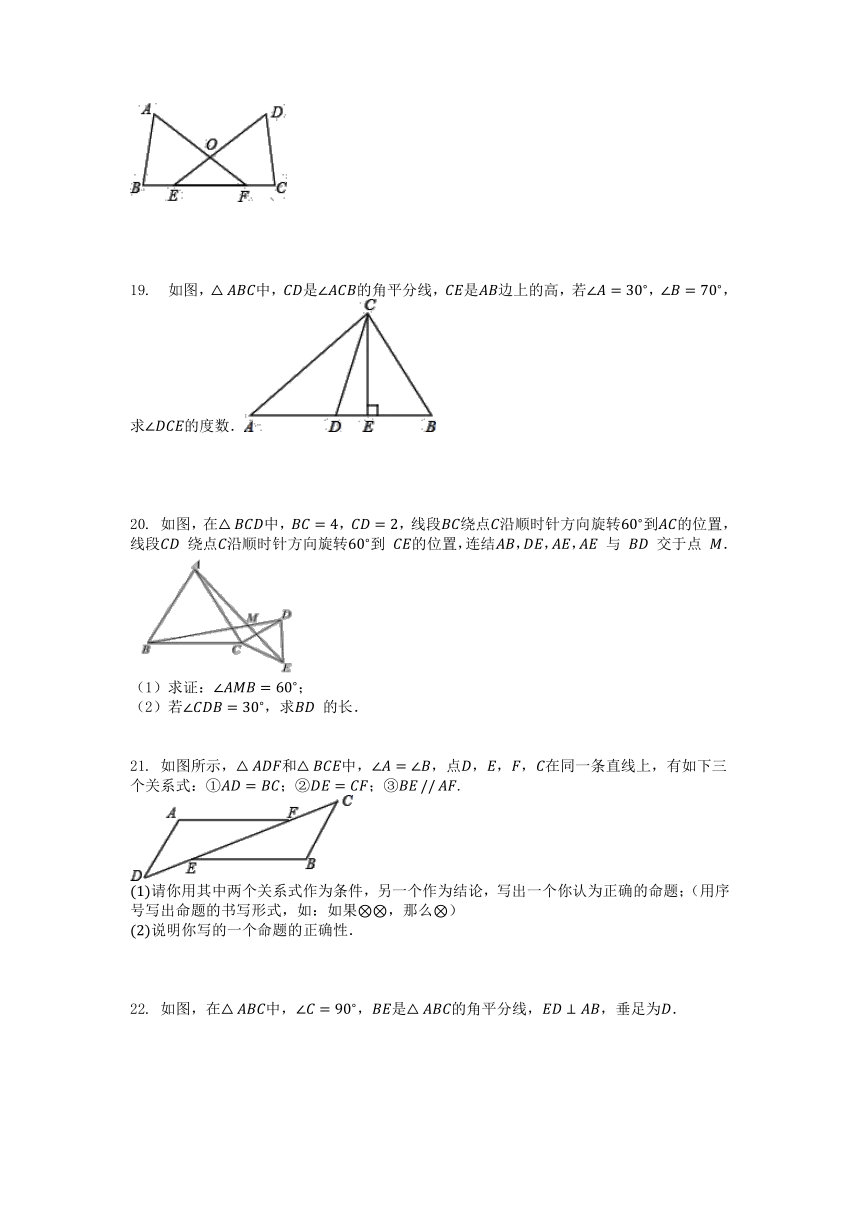
8.如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2
,依此类推,∠A4BC与∠A4CD的平分线相交于点A5
,则∠A5的度数为(??
)
A.?19.2°???
?B.?8°???
C.?6°?????
???D.?3°
9.如图,在△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长为(??
)
A.?3????
??B.?4????????
?C.?5??
??????D.?6
10.已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,对于上述的两个判断,下列说法正确的是(
)
A.①正确,②错误
B.①错误,②正确
C.①,②都错误
D.①,②都正确
二、填空题(每小题4分,共24分)
11.命题“如果a+b=0,那么a,b互为相反数”的逆命题为________.
12.等腰三角形的两边长分别为
,其周长为________cm.
13.如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=________度.
14.将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为________.
15.如图,AC=BC,请你添加一对边或一对角相等的条件,使AD=BE.你所添加的条件是________.
16.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是________.
三、
解答题
17.
把下列各图分成若干个全等图形,请在原图上用虚线标出来.
?
18.
已知:如图,、、、四点在同一条直线上,,,.求证:.
?
19.
如图,中,是的角平分线,是边上的高,若,,求的度数.
?
20.
如图,在中,,,线段绕点沿顺时针方向旋转到的位置,线段
绕点沿顺时针方向旋转到
的位置,连结,,,
与
交于点
.
(1)求证:;
(2)若,求
的长.
21.
如图所示,和中,,点,,,在同一条直线上,有如下三个关系式:①;②;③.
请你用其中两个关系式作为条件,另一个作为结论,写出一个你认为正确的命题;(用序号写出命题的书写形式,如:如果,那么)
说明你写的一个命题的正确性.
22.
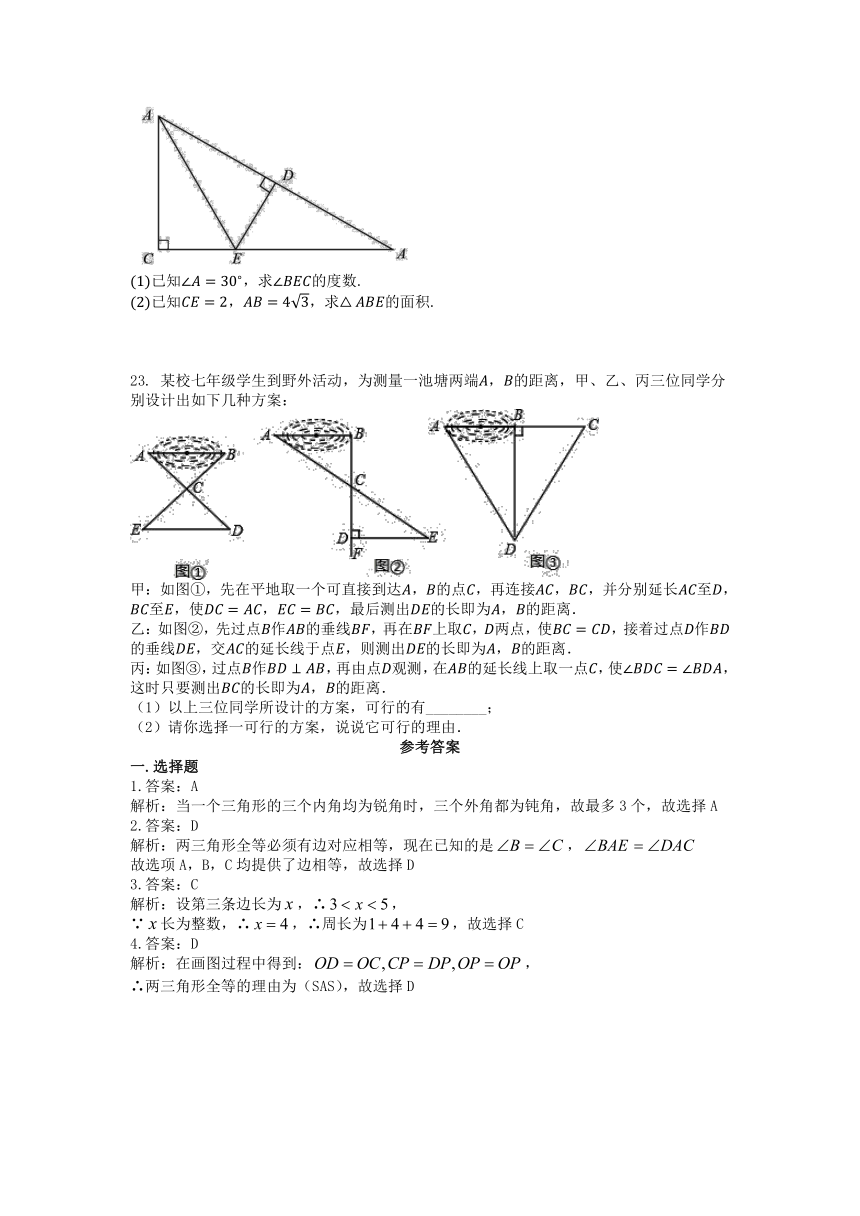
如图,在中,,是的角平分线,,垂足为.
已知,求的度数.
已知,,求的面积.
23.
某校七年级学生到野外活动,为测量一池塘两端,的距离,甲、乙、丙三位同学分别设计出如下几种方案:
甲:如图①,先在平地取一个可直接到达,的点,再连接,,并分别延长至,至,使,,最后测出的长即为,的距离.
乙:如图②,先过点作的垂线,再在上取,两点,使,接着过点作的垂线,交的延长线于点,则测出的长即为,的距离.
丙:如图③,过点作,再由点观测,在的延长线上取一点,使,这时只要测出的长即为,的距离.
(1)以上三位同学所设计的方案,可行的有________;
(2)请你选择一可行的方案,说说它可行的理由.
参考答案
一.选择题
1.答案:A
解析:当一个三角形的三个内角均为锐角时,三个外角都为钝角,故最多3个,故选择A
2.答案:D
解析:两三角形全等必须有边对应相等,现在已知的是,
故选项A,B,C均提供了边相等,故选择D
3.答案:C
解析:设第三条边长为,∴,
∵长为整数,∴,∴周长为,故选择C
4.答案:D
解析:在画图过程中得到:,
∴两三角形全等的理由为(SAS),故选择D
5.答案:A
解析:过C作交ED的延长线于H,连接FH,
∴∵
∴△EDB≌△HCD,∴,,
∵,∴DF是线段EH的垂直平分线,
∴,
∵在△FCH中,
∴,故选择A
6.答案:D
解析:过点E作EH⊥AB于H,作EG⊥AF于G,则∠EHB=∠EGF=90°,
∵AD为角平分线,
∴EH=EG,
又∵E为BF中点,
∴EB=EF,
∴Rt△EHB≌Rt△EGF(HL),
∴∠BEH=∠FEG,
∵∠EAH=∠EAG,∠EHA=∠EGA,
∴∠AEH=∠AEG,
∴∠AEB=∠AEF=90°,即AE⊥BF,
又∵∠ACB=90°,∠ADC=∠BDE,
∴∠CAD=∠CBF,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(ASA),
∴AD=BF,CD=CF,故A、B选项正确;
∴AC+CD=AC+CF=AF,
又∵AE垂直平分BF,
∴AF=AB,
∴AC+CD=AB,故C正确;
∵EF>CD,
∴BE>CF,故D错误.
故选:D.
7.答案:D
解析:∵AD是中线,∴,
∵,,∴△BDF≌△CDE(SAS)∴,故①④正确;
∵,∴△ABD和△ACD面积相等,故②正确;
∵△BDF≌△CDE,∴,∴,故③正确;
故正确答案①②③④,故选择D
8.答案:D
解析:∵∠BA1C+∠A1BC=∠A1CD,2∠A1CD=∠ACD=∠BAC+∠ABC,
∴2(∠BA1C+∠A1BC)=∠BAC+∠ABC,2∠BA1C+2∠A1BC=∠BAC+∠ABC.
∵2∠A1BC=∠ABC,
∴2∠BA1C=∠BAC.
同理,可得2∠BA2C=∠BA1C,2∠BA3C=∠BA2C,2∠BA4C=∠BA3C,2∠BA5C=∠BA4C,
∴∠BA5C=∠BA4C=∠BA3C=∠BA2C=∠BA1C=∠BAC=96°÷32=3°.
故答案为:D.
9.答案:B
解析:∵,,∴,
∴,,
∴,∴△BDF≌△ADC,∴,
故选择B
10.答案:A
解析:∵△A1B1C1,△A2B2C2的周长相等,A1B1=A2B2,A1C1=A2C2
∴,∴△≌△(SAS)故①正确;
∵若∠A1=∠A2,∠B1=∠B2,只能得到,周长相等不能得到位对应边相等,
故无法判断两三角形全等,故②错误,故选择A
二.填空题
11解:逆命题为:如果a,b互为相反数,那么a+b=0.
故答案为:如果a,b互为相反数,那么a+b=0.
12.解:由题意知,应分两种情况:(1)当腰长为
时,三角形三边长为
,不能构成三角形;(2)当腰长为
时,三角形三边长为
,周长
故答案为32
13.解:∵AB∥CD,
∴∠OED=∠2,
∵OA⊥OB,
∴∠O=90°,
∵∠1=∠OED+∠O=142°,
∴∠2=∠1﹣∠O=142°﹣90°=52°,
故答案为:52.
14.解:∵BC∥DE,
∴∠BCE=∠E=30°,
∴∠ACF=∠ACB-∠BCE=45°-30°=15°,
在Rt△ACF中,∠AFC=90°-∠ACF=90°-15°=75°.
故答案为:75°.
15.解:因为AC=BC,
∠C=∠C,
所以添加∠A=∠B或∠ADC=∠BEC或
CE=CD,可得△ADC与△BEC全等,
利用全等三角形的性质得出AD=BE,
故答案为:
∠A=∠B或∠ADC=∠BEC或CE=CD.
16.解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,
∵S△ACF=S△BCF=S△ABC=×12=6,
∴S△CGE=S△ACF=×6=2,S△BGF=S△BCF=×6=2,
∴S阴影=S△CGE+S△BGF=4.
故答案为4.
三、
解答题
17.
【答案】
【解答】
18.
【答案】
证明:∵
,
∴
,
∴
,
在和中
∴
,
∴
.
【解答】
证明:∵
,
∴
,
∴
,
在和中
∴
,
∴
.
19.【答案】
解:∵
,,
∴
∵
平分,
∴
∵
是边上的高
∴
∴
.
【解答】
解:∵
,,
∴
∵
平分,
∴
∵
是边上的高
∴
∴
.
20.【答案】
【解答】
此题暂无解答
21.【答案】
解:如果①,③,那么②;如果②,③,那么①;
对于命题“如果①,③,那么②”证明如下:
∵
,
∴
.
∵
,,
∴
,
∴
.
∴
,即;
对于命题“如果②,③,那么①”证明如下:
∵
,
∴
.
∵
,
∴
,即.
∵
,
∴
,
∴
.
【解答】
解:如果①,③,那么②;如果②,③,那么①;
对于命题“如果①,③,那么②”证明如下:
∵
,
∴
.
∵
,,
∴
,
∴
.
∴
,即;
对于命题“如果②,③,那么①”证明如下:
∵
,
∴
.
∵
,
∴
,即.
∵
,
∴
,
∴
.
22.【答案】
解:由题可得,
.
平分,
,
.
平分,,,
,
.
【解答】
解:由题可得,
.
平分,
,
.
平分,,,
,
.
23.【答案】
解:(1)甲、乙、丙;
(2)答案不唯一.
选甲:在和中,
∴
,
∴
;
选乙:∵
,,
∴
,
在和中,
∴
,
∴
;
选丙:
在和中,
∴
,
∴
.
【解答】
解:(1)甲、乙、丙;
(2)答案不唯一.
选甲:在和中,
∴
,
∴
;
选乙:∵
,,
∴
,
在和中,
∴
,
∴
;
选丙:
在和中,
∴
,
∴
.
1章三角形的初步认识单元测试卷
一、选择题
1.在一个三角形的三个外角中,钝角的个数最多有(
)
A.3个
B.2个
C.1个
D.0个
2.如图,D在AB上,E在AC上,且∠B=∠C,则再添加下列条件,仍无法判定△ABE≌△ACD的是(
)
A.AD=AE
B.AB=AC
C.BE=CD
D.∠AEB=∠ADC
3.已知三角形的两边分别为1和4,第三边长为整数
,则该三角形的周长为(
?
)
A.?7?
????B.?8???????
?C.?9??????
?D.?10
4.尺规作图作的平分线方法如下:如图,以点O为圆心,任意长为半径画弧分别交OA,OB于点C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP,由作法得的根据是(
)
A.
SAS
B.
ASA
C.
AAS
D.
SSS
5.如图,AD是的中线,点E,F分别在AB,AC上(点E,F不与端点重合),且.则线段BE,CF,EF的关系是(
)
A.
B.
C.
D.
与EF的大小关系不确定
6.如图△ABC,AC=BC,∠ACB=90°,AD为角平分线,延长AD交BF于E,E为BF中点,下列结论错误的是(?
?
)
A.?AD=BF???
?B.?CF=CD????
?
C.?AC+CD=AB???
?D.?BE=CF
7.
如图,
AD是的中线,E,F分别是AD和AD延长线上的点,且,连结BF,CE.下列说法:①CE=BF;②△ABD和△ACD面积相等;
③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
8.如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2
,依此类推,∠A4BC与∠A4CD的平分线相交于点A5
,则∠A5的度数为(??
)
A.?19.2°???
?B.?8°???
C.?6°?????
???D.?3°
9.如图,在△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长为(??
)
A.?3????
??B.?4????????
?C.?5??
??????D.?6
10.已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,对于上述的两个判断,下列说法正确的是(
)
A.①正确,②错误
B.①错误,②正确
C.①,②都错误
D.①,②都正确
二、填空题(每小题4分,共24分)
11.命题“如果a+b=0,那么a,b互为相反数”的逆命题为________.
12.等腰三角形的两边长分别为
,其周长为________cm.
13.如图,直线AB∥CD,OA⊥OB,若∠1=142°,则∠2=________度.
14.将一副三角板如图放置,使点A落在DE上,若BC∥DE,则∠AFC的度数为________.
15.如图,AC=BC,请你添加一对边或一对角相等的条件,使AD=BE.你所添加的条件是________.
16.如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是________.
三、
解答题
17.
把下列各图分成若干个全等图形,请在原图上用虚线标出来.
?
18.
已知:如图,、、、四点在同一条直线上,,,.求证:.
?
19.
如图,中,是的角平分线,是边上的高,若,,求的度数.
?
20.
如图,在中,,,线段绕点沿顺时针方向旋转到的位置,线段
绕点沿顺时针方向旋转到
的位置,连结,,,
与
交于点
.
(1)求证:;
(2)若,求
的长.
21.
如图所示,和中,,点,,,在同一条直线上,有如下三个关系式:①;②;③.
请你用其中两个关系式作为条件,另一个作为结论,写出一个你认为正确的命题;(用序号写出命题的书写形式,如:如果,那么)
说明你写的一个命题的正确性.
22.
如图,在中,,是的角平分线,,垂足为.
已知,求的度数.
已知,,求的面积.
23.
某校七年级学生到野外活动,为测量一池塘两端,的距离,甲、乙、丙三位同学分别设计出如下几种方案:
甲:如图①,先在平地取一个可直接到达,的点,再连接,,并分别延长至,至,使,,最后测出的长即为,的距离.
乙:如图②,先过点作的垂线,再在上取,两点,使,接着过点作的垂线,交的延长线于点,则测出的长即为,的距离.
丙:如图③,过点作,再由点观测,在的延长线上取一点,使,这时只要测出的长即为,的距离.
(1)以上三位同学所设计的方案,可行的有________;
(2)请你选择一可行的方案,说说它可行的理由.
参考答案
一.选择题
1.答案:A
解析:当一个三角形的三个内角均为锐角时,三个外角都为钝角,故最多3个,故选择A
2.答案:D
解析:两三角形全等必须有边对应相等,现在已知的是,
故选项A,B,C均提供了边相等,故选择D
3.答案:C
解析:设第三条边长为,∴,
∵长为整数,∴,∴周长为,故选择C
4.答案:D
解析:在画图过程中得到:,
∴两三角形全等的理由为(SAS),故选择D
5.答案:A
解析:过C作交ED的延长线于H,连接FH,
∴∵
∴△EDB≌△HCD,∴,,
∵,∴DF是线段EH的垂直平分线,
∴,
∵在△FCH中,
∴,故选择A
6.答案:D
解析:过点E作EH⊥AB于H,作EG⊥AF于G,则∠EHB=∠EGF=90°,
∵AD为角平分线,
∴EH=EG,
又∵E为BF中点,
∴EB=EF,
∴Rt△EHB≌Rt△EGF(HL),
∴∠BEH=∠FEG,
∵∠EAH=∠EAG,∠EHA=∠EGA,
∴∠AEH=∠AEG,
∴∠AEB=∠AEF=90°,即AE⊥BF,
又∵∠ACB=90°,∠ADC=∠BDE,
∴∠CAD=∠CBF,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(ASA),
∴AD=BF,CD=CF,故A、B选项正确;
∴AC+CD=AC+CF=AF,
又∵AE垂直平分BF,
∴AF=AB,
∴AC+CD=AB,故C正确;
∵EF>CD,
∴BE>CF,故D错误.
故选:D.
7.答案:D
解析:∵AD是中线,∴,
∵,,∴△BDF≌△CDE(SAS)∴,故①④正确;
∵,∴△ABD和△ACD面积相等,故②正确;
∵△BDF≌△CDE,∴,∴,故③正确;
故正确答案①②③④,故选择D
8.答案:D
解析:∵∠BA1C+∠A1BC=∠A1CD,2∠A1CD=∠ACD=∠BAC+∠ABC,
∴2(∠BA1C+∠A1BC)=∠BAC+∠ABC,2∠BA1C+2∠A1BC=∠BAC+∠ABC.
∵2∠A1BC=∠ABC,
∴2∠BA1C=∠BAC.
同理,可得2∠BA2C=∠BA1C,2∠BA3C=∠BA2C,2∠BA4C=∠BA3C,2∠BA5C=∠BA4C,
∴∠BA5C=∠BA4C=∠BA3C=∠BA2C=∠BA1C=∠BAC=96°÷32=3°.
故答案为:D.
9.答案:B
解析:∵,,∴,
∴,,
∴,∴△BDF≌△ADC,∴,
故选择B
10.答案:A
解析:∵△A1B1C1,△A2B2C2的周长相等,A1B1=A2B2,A1C1=A2C2
∴,∴△≌△(SAS)故①正确;
∵若∠A1=∠A2,∠B1=∠B2,只能得到,周长相等不能得到位对应边相等,
故无法判断两三角形全等,故②错误,故选择A
二.填空题
11解:逆命题为:如果a,b互为相反数,那么a+b=0.
故答案为:如果a,b互为相反数,那么a+b=0.
12.解:由题意知,应分两种情况:(1)当腰长为
时,三角形三边长为
,不能构成三角形;(2)当腰长为
时,三角形三边长为
,周长
故答案为32
13.解:∵AB∥CD,
∴∠OED=∠2,
∵OA⊥OB,
∴∠O=90°,
∵∠1=∠OED+∠O=142°,
∴∠2=∠1﹣∠O=142°﹣90°=52°,
故答案为:52.
14.解:∵BC∥DE,
∴∠BCE=∠E=30°,
∴∠ACF=∠ACB-∠BCE=45°-30°=15°,
在Rt△ACF中,∠AFC=90°-∠ACF=90°-15°=75°.
故答案为:75°.
15.解:因为AC=BC,
∠C=∠C,
所以添加∠A=∠B或∠ADC=∠BEC或
CE=CD,可得△ADC与△BEC全等,
利用全等三角形的性质得出AD=BE,
故答案为:
∠A=∠B或∠ADC=∠BEC或CE=CD.
16.解:∵△ABC的三条中线AD、BE,CF交于点G,
∴S△CGE=S△AGE=S△ACF,S△BGF=S△BGD=S△BCF,
∵S△ACF=S△BCF=S△ABC=×12=6,
∴S△CGE=S△ACF=×6=2,S△BGF=S△BCF=×6=2,
∴S阴影=S△CGE+S△BGF=4.
故答案为4.
三、
解答题
17.
【答案】
【解答】
18.
【答案】
证明:∵
,
∴
,
∴
,
在和中
∴
,
∴
.
【解答】
证明:∵
,
∴
,
∴
,
在和中
∴
,
∴
.
19.【答案】
解:∵
,,
∴
∵
平分,
∴
∵
是边上的高
∴
∴
.
【解答】
解:∵
,,
∴
∵
平分,
∴
∵
是边上的高
∴
∴
.
20.【答案】
【解答】
此题暂无解答
21.【答案】
解:如果①,③,那么②;如果②,③,那么①;
对于命题“如果①,③,那么②”证明如下:
∵
,
∴
.
∵
,,
∴
,
∴
.
∴
,即;
对于命题“如果②,③,那么①”证明如下:
∵
,
∴
.
∵
,
∴
,即.
∵
,
∴
,
∴
.
【解答】
解:如果①,③,那么②;如果②,③,那么①;
对于命题“如果①,③,那么②”证明如下:
∵
,
∴
.
∵
,,
∴
,
∴
.
∴
,即;
对于命题“如果②,③,那么①”证明如下:
∵
,
∴
.
∵
,
∴
,即.
∵
,
∴
,
∴
.
22.【答案】
解:由题可得,
.
平分,
,
.
平分,,,
,
.
【解答】
解:由题可得,
.
平分,
,
.
平分,,,
,
.
23.【答案】
解:(1)甲、乙、丙;
(2)答案不唯一.
选甲:在和中,
∴
,
∴
;
选乙:∵
,,
∴
,
在和中,
∴
,
∴
;
选丙:
在和中,
∴
,
∴
.
【解答】
解:(1)甲、乙、丙;
(2)答案不唯一.
选甲:在和中,
∴
,
∴
;
选乙:∵
,,
∴
,
在和中,
∴
,
∴
;
选丙:
在和中,
∴
,
∴
.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
