第3章 圆的基本性质单元测试卷-2021-2022学年浙教版数学九年级上册(Word版含答案)
文档属性
| 名称 | 第3章 圆的基本性质单元测试卷-2021-2022学年浙教版数学九年级上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 249.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 15:03:16 | ||
图片预览




文档简介
2021-2022学年九年级上册数学第3章
圆的基本性质
单元测试卷
一、选择题
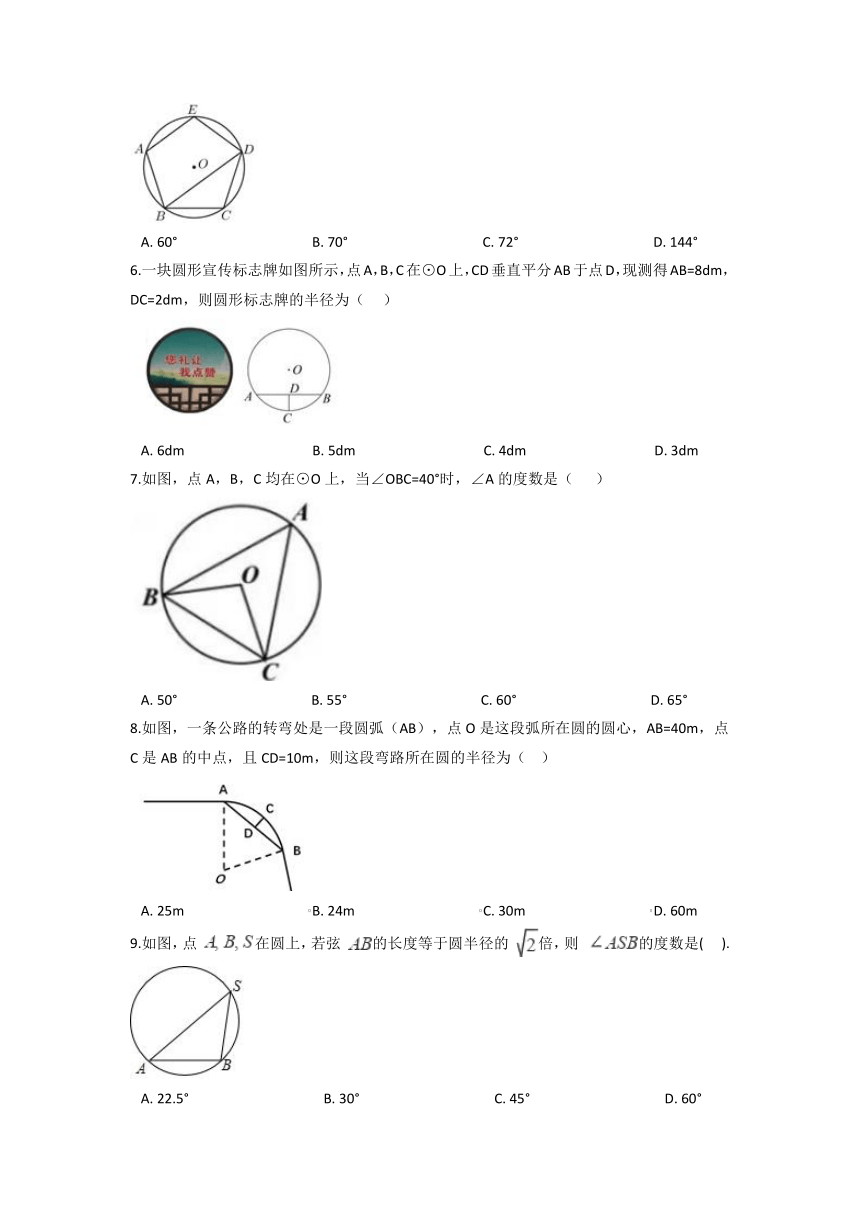
1.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是(???
)
A.?∠B??????????????????????????????????????B.?∠C??????????????????????????????????????C.?∠DEB??????????????????????????????????????D.?∠D
2.若扇形的圆心角为90°,半径为6,则该扇形的弧长为(
??)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
3.如图,△ABC内接于⊙O,∠B=65°,∠C=70°,若BC=2
,则
的长为(
??)
A.?π?????????????????????????????????????B.?π?????????????????????????????????????C.?2π?????????????????????????????????????D.?π
4.如图,AD是⊙O的直径,
,若∠AOB=40°,则圆周角∠BPC的度数是(??
)
A.?40°???????????????????????????????????????B.?50°???????????????????????????????????????C.?60°???????????????????????????????????????D.?70°
5.如图,已知正五边形
ABCDE内接于⊙O,连结BD,则∠ABD的度数是(
??)
A.?60°??????????????????????????????????????B.?70°??????????????????????????????????????C.?72°??????????????????????????????????????D.?144°
6.一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D,现测得AB=8dm,DC=2dm,则圆形标志牌的半径为(
???)
A.?6dm????????????????????????????????????B.?5dm????????????????????????????????????C.?4dm????????????????????????????????????D.?3dm
7.如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是(????
)
A.?50°???????????????????????????????????????B.?55°???????????????????????????????????????C.?60°???????????????????????????????????????D.?65°
8.如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心,AB=40m,点C是AB的中点,且CD=10m,则这段弯路所在圆的半径为(
??)
A.?25m????????????????????????????????????B.?24m????????????????????????????????????C.?30m????????????????????????????????????D.?60m
9.如图,点
在圆上,若弦
的长度等于圆半径的
倍,则
的度数是(???
).
A.?22.5°??????????????????????????????????????B.?30°??????????????????????????????????????C.?45°??????????????????????????????????????D.?60°
10.如图,四边形
是菱形,
经过点
、
、
,与
相交于点
,连接
、
.若
,则
的度数为(??
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
11.如图,
的斜边在
轴上,
,含
角的顶点与原点重合,直角顶点
在第二象限,将
绕原点顺时针旋转
后得到
,则
点的对应点
的坐标是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
12.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为(???
)
A.?6π????????????????????????????????????B.?π????????????????????????????????????C.?π????????????????????????????????????D.?2π
二.填空题(共6小题,满分24分,每小题4分)
13.已知一个扇形的面积为12πcm2,圆心角的度数为108°,则它的弧长为
.
14.⊙O的圆心是原点O(0,0),半径为5,点A(3,a)在⊙O上,如果点A在第一象限内,那么a=
.
15.如图,在平面直角坐标系中,将点P(4,6)绕坐标原点O顺时针旋转90°得到点Q,则点Q的坐标为
.
16.如图,将△ABC绕点A顺时针旋转得到△AB'C',点C′恰好落在线段AB上,连接BB'.若AC=1,AB=3,则BC′=
.
17.如图,AB为⊙O直径,点C、D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD=
度.
18.如图,AB是⊙O的直径,C是⊙O上一点,∠ACB的平分线交⊙O于D,且AB=10,则AD的长为
.
三、解答题
19.如图,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径.求证:∠BAM=∠CAP.
20.如图,在△ABC中,∠C=45°,AB=2.
(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O;
(2)求△ABC的外接圆⊙O的直径.
21.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连结BD交CF于点G,连结CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
23.如图,在矩形ABCD中,AD=2,以B为圆心,BC为半径画弧交AD于F.
(1)若的长为π,求圆心角∠CBF的度数;
(2)在(1)的条件下,求图中阴影部分的面积.(结果保留根号及π)
24.如图,⊙O的直径AB=12
cm,有一条定长为8
cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.
(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
参考答案
一、选择题
1.
D
2.
C
3.
A
4.
B
5.
C
6.
B
7.
A
8.
A
9.
C
10.
C
11.
A
12.
A
二.填空题
13.解:设扇形的半径为Rcm,
∵扇形的面积为12πcm2,圆心角的度数为108°,
∴=12π,
解得:R=2,
∴弧长为=π(cm),
故答案为:πcm.
14.解:∵⊙O的圆心是原点O(0,0),半径为5,点A(3,a)在⊙O上,
∴|a|==4,
∵点A在第一象限内,
∴a=4.
故答案为:4.
15.解:作图如下,
∵∠MPO+∠POM=90°,∠QON+∠POM=90°,
∴∠MPO=∠QON,
在△PMO和△ONQ中,
,
∴△PMO≌△ONQ(AAS),
∴PM=ON,OM=QN,
∵P点坐标为(4,6),
∴Q点坐标为(6,﹣4),
故答案为(6,﹣4).
16.解:∵△ABC绕点A顺时针旋转得到△AB'C',点C′恰好落在线段AB上,
∴AC′=AC=1,
∴BC′=AB﹣AC′=3﹣1=2.
故答案为2.
17.解:∵AD∥OC,
∴∠BOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
18.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ACB的平分线交⊙O于D,
∴∠ACD=∠BCD,
∴=,
∴AD=BD,
∴△ABD为等腰直角三角形,
∴AD=AB=10×=5.
故答案为5.
三、解答题
19.证明:连结BM.∵AP⊥BC,
∴∠CAP=90°-∠C.
∵AM为⊙O的直径,∴∠ABM=90°,
∴∠BAM=90°-∠M.
又∵∠M=∠C,
∴∠BAM=∠CAP.
20.解:(1)作图略.
(2)作直径AD,连结BD.
∵AD是直径,∴∠ABD=90°.
∵∠D=∠C=45°,∴AB=BD=2.
∴AD===2
,即△ABC的外接圆⊙O的直径为2
.
21.解:(1)△AB′C′如图所示.
(2)根据网格图,可知AB==5.
易知线段AB在变换到AB′的过程中,扫过区域为圆心角为90°,半径为5的扇形,其面积S=π·52=π.
22.(1)证明:∵C是的中点,∴=.
∵AB是⊙O的直径,且CF⊥AB,
∴=,∴=,∴CD=BF.
在△BFG和△CDG中,
∵
∴△BFG≌△CDG(AAS).
(2)解:连结OF,设⊙O的半径为r,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴BD2=AB2-AD2,即BD2=(2r)2-22.
在Rt△OEF中,OF2=OE2+EF2,
即EF2=r2-(r-2)2.
由(1)知==,∴=,
∴BD=CF,易得EF=CE,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2-22=4[r2-(r-2)2],
解得r=1(舍去)或r=3,
∴BF2=EF2+BE2=32-(3-2)2+22=12,
∴BF=2.
23.解:(1)设∠CBF=n°,
∵的长为π,半径R=BC=AD=2,
∴=π,∴n=60,
即∠CBF的度数为60°.
(2)∵∠CBF=60°,且四边形ABCD为矩形,∴∠ABF=30°.
在Rt△ABF中,易得AF=BF=AD=1,
∴AB===.
易得S扇形CBF==π,
S矩形ABCD=AD·AB=2×=2
,
S△ABF=AF·AB=×1×=,∴S阴影=S矩形ABCD-(S扇形CBF+S△ABF)=2-=-π.
24.(1)证明:过点O作OH⊥CD于点H,易得H为CD的中点.
∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,
易得O为EF的中点,即OE=OF.
又∵OA=OB,
∴AE=OA-OE=OB-OF=BF,即AE=BF.
(2)解:四边形CDFE的面积为定值.证明如下:∵动弦CD在滑动的过程中,条件EC⊥CD,FD⊥CD不变,∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,易得S四边形CDFE=OH·CD.连结OC,由勾股定理得OH===2(cm).又∵CD=8
cm,∴S四边形CDFE=OH·CD=2×8=16(cm2),是常数.综上,四边形CDFE的面积为定值,为16cm2.
圆的基本性质
单元测试卷
一、选择题
1.如图,A,B,C,D是⊙O上的点,则图中与∠A相等的角是(???
)
A.?∠B??????????????????????????????????????B.?∠C??????????????????????????????????????C.?∠DEB??????????????????????????????????????D.?∠D
2.若扇形的圆心角为90°,半径为6,则该扇形的弧长为(
??)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
3.如图,△ABC内接于⊙O,∠B=65°,∠C=70°,若BC=2
,则
的长为(
??)
A.?π?????????????????????????????????????B.?π?????????????????????????????????????C.?2π?????????????????????????????????????D.?π
4.如图,AD是⊙O的直径,
,若∠AOB=40°,则圆周角∠BPC的度数是(??
)
A.?40°???????????????????????????????????????B.?50°???????????????????????????????????????C.?60°???????????????????????????????????????D.?70°
5.如图,已知正五边形
ABCDE内接于⊙O,连结BD,则∠ABD的度数是(
??)
A.?60°??????????????????????????????????????B.?70°??????????????????????????????????????C.?72°??????????????????????????????????????D.?144°
6.一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D,现测得AB=8dm,DC=2dm,则圆形标志牌的半径为(
???)
A.?6dm????????????????????????????????????B.?5dm????????????????????????????????????C.?4dm????????????????????????????????????D.?3dm
7.如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是(????
)
A.?50°???????????????????????????????????????B.?55°???????????????????????????????????????C.?60°???????????????????????????????????????D.?65°
8.如图,一条公路的转弯处是一段圆弧(AB),点O是这段弧所在圆的圆心,AB=40m,点C是AB的中点,且CD=10m,则这段弯路所在圆的半径为(
??)
A.?25m????????????????????????????????????B.?24m????????????????????????????????????C.?30m????????????????????????????????????D.?60m
9.如图,点
在圆上,若弦
的长度等于圆半径的
倍,则
的度数是(???
).
A.?22.5°??????????????????????????????????????B.?30°??????????????????????????????????????C.?45°??????????????????????????????????????D.?60°
10.如图,四边形
是菱形,
经过点
、
、
,与
相交于点
,连接
、
.若
,则
的度数为(??
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
11.如图,
的斜边在
轴上,
,含
角的顶点与原点重合,直角顶点
在第二象限,将
绕原点顺时针旋转
后得到
,则
点的对应点
的坐标是(??
)
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
12.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为(???
)
A.?6π????????????????????????????????????B.?π????????????????????????????????????C.?π????????????????????????????????????D.?2π
二.填空题(共6小题,满分24分,每小题4分)
13.已知一个扇形的面积为12πcm2,圆心角的度数为108°,则它的弧长为
.
14.⊙O的圆心是原点O(0,0),半径为5,点A(3,a)在⊙O上,如果点A在第一象限内,那么a=
.
15.如图,在平面直角坐标系中,将点P(4,6)绕坐标原点O顺时针旋转90°得到点Q,则点Q的坐标为
.
16.如图,将△ABC绕点A顺时针旋转得到△AB'C',点C′恰好落在线段AB上,连接BB'.若AC=1,AB=3,则BC′=
.
17.如图,AB为⊙O直径,点C、D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD=
度.
18.如图,AB是⊙O的直径,C是⊙O上一点,∠ACB的平分线交⊙O于D,且AB=10,则AD的长为
.
三、解答题
19.如图,△ABC的三个顶点都在⊙O上,AP⊥BC于P,AM为⊙O的直径.求证:∠BAM=∠CAP.
20.如图,在△ABC中,∠C=45°,AB=2.
(1)尺规作图(不写作法,保留作图痕迹):作△ABC的外接圆⊙O;
(2)求△ABC的外接圆⊙O的直径.
21.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
22.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连结BD交CF于点G,连结CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
23.如图,在矩形ABCD中,AD=2,以B为圆心,BC为半径画弧交AD于F.
(1)若的长为π,求圆心角∠CBF的度数;
(2)在(1)的条件下,求图中阴影部分的面积.(结果保留根号及π)
24.如图,⊙O的直径AB=12
cm,有一条定长为8
cm的动弦CD在上滑动(点C不与A,B重合,点D也不与A,B重合),且CE⊥CD交AB于点E,DF⊥CD交AB于点F.
(1)求证:AE=BF;
(2)在动弦CD滑动的过程中,四边形CDFE的面积是否为定值?若是定值,请给出证明,并求出这个定值;若不是,请说明理由.
参考答案
一、选择题
1.
D
2.
C
3.
A
4.
B
5.
C
6.
B
7.
A
8.
A
9.
C
10.
C
11.
A
12.
A
二.填空题
13.解:设扇形的半径为Rcm,
∵扇形的面积为12πcm2,圆心角的度数为108°,
∴=12π,
解得:R=2,
∴弧长为=π(cm),
故答案为:πcm.
14.解:∵⊙O的圆心是原点O(0,0),半径为5,点A(3,a)在⊙O上,
∴|a|==4,
∵点A在第一象限内,
∴a=4.
故答案为:4.
15.解:作图如下,
∵∠MPO+∠POM=90°,∠QON+∠POM=90°,
∴∠MPO=∠QON,
在△PMO和△ONQ中,
,
∴△PMO≌△ONQ(AAS),
∴PM=ON,OM=QN,
∵P点坐标为(4,6),
∴Q点坐标为(6,﹣4),
故答案为(6,﹣4).
16.解:∵△ABC绕点A顺时针旋转得到△AB'C',点C′恰好落在线段AB上,
∴AC′=AC=1,
∴BC′=AB﹣AC′=3﹣1=2.
故答案为2.
17.解:∵AD∥OC,
∴∠BOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
18.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ACB的平分线交⊙O于D,
∴∠ACD=∠BCD,
∴=,
∴AD=BD,
∴△ABD为等腰直角三角形,
∴AD=AB=10×=5.
故答案为5.
三、解答题
19.证明:连结BM.∵AP⊥BC,
∴∠CAP=90°-∠C.
∵AM为⊙O的直径,∴∠ABM=90°,
∴∠BAM=90°-∠M.
又∵∠M=∠C,
∴∠BAM=∠CAP.
20.解:(1)作图略.
(2)作直径AD,连结BD.
∵AD是直径,∴∠ABD=90°.
∵∠D=∠C=45°,∴AB=BD=2.
∴AD===2
,即△ABC的外接圆⊙O的直径为2
.
21.解:(1)△AB′C′如图所示.
(2)根据网格图,可知AB==5.
易知线段AB在变换到AB′的过程中,扫过区域为圆心角为90°,半径为5的扇形,其面积S=π·52=π.
22.(1)证明:∵C是的中点,∴=.
∵AB是⊙O的直径,且CF⊥AB,
∴=,∴=,∴CD=BF.
在△BFG和△CDG中,
∵
∴△BFG≌△CDG(AAS).
(2)解:连结OF,设⊙O的半径为r,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴BD2=AB2-AD2,即BD2=(2r)2-22.
在Rt△OEF中,OF2=OE2+EF2,
即EF2=r2-(r-2)2.
由(1)知==,∴=,
∴BD=CF,易得EF=CE,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2-22=4[r2-(r-2)2],
解得r=1(舍去)或r=3,
∴BF2=EF2+BE2=32-(3-2)2+22=12,
∴BF=2.
23.解:(1)设∠CBF=n°,
∵的长为π,半径R=BC=AD=2,
∴=π,∴n=60,
即∠CBF的度数为60°.
(2)∵∠CBF=60°,且四边形ABCD为矩形,∴∠ABF=30°.
在Rt△ABF中,易得AF=BF=AD=1,
∴AB===.
易得S扇形CBF==π,
S矩形ABCD=AD·AB=2×=2
,
S△ABF=AF·AB=×1×=,∴S阴影=S矩形ABCD-(S扇形CBF+S△ABF)=2-=-π.
24.(1)证明:过点O作OH⊥CD于点H,易得H为CD的中点.
∵CE⊥CD,DF⊥CD,∴EC∥OH∥FD,
易得O为EF的中点,即OE=OF.
又∵OA=OB,
∴AE=OA-OE=OB-OF=BF,即AE=BF.
(2)解:四边形CDFE的面积为定值.证明如下:∵动弦CD在滑动的过程中,条件EC⊥CD,FD⊥CD不变,∴CE∥DF不变.由此可知,四边形CDFE为直角梯形或矩形,易得S四边形CDFE=OH·CD.连结OC,由勾股定理得OH===2(cm).又∵CD=8
cm,∴S四边形CDFE=OH·CD=2×8=16(cm2),是常数.综上,四边形CDFE的面积为定值,为16cm2.
同课章节目录
