2021-2022 学年浙教版九年级数学上册1.4 二次函数的应用 练习(word版、含解析)
文档属性
| 名称 | 2021-2022 学年浙教版九年级数学上册1.4 二次函数的应用 练习(word版、含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 881.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 15:25:38 | ||
图片预览



文档简介
1.4
二次函数的应用
一、单选题
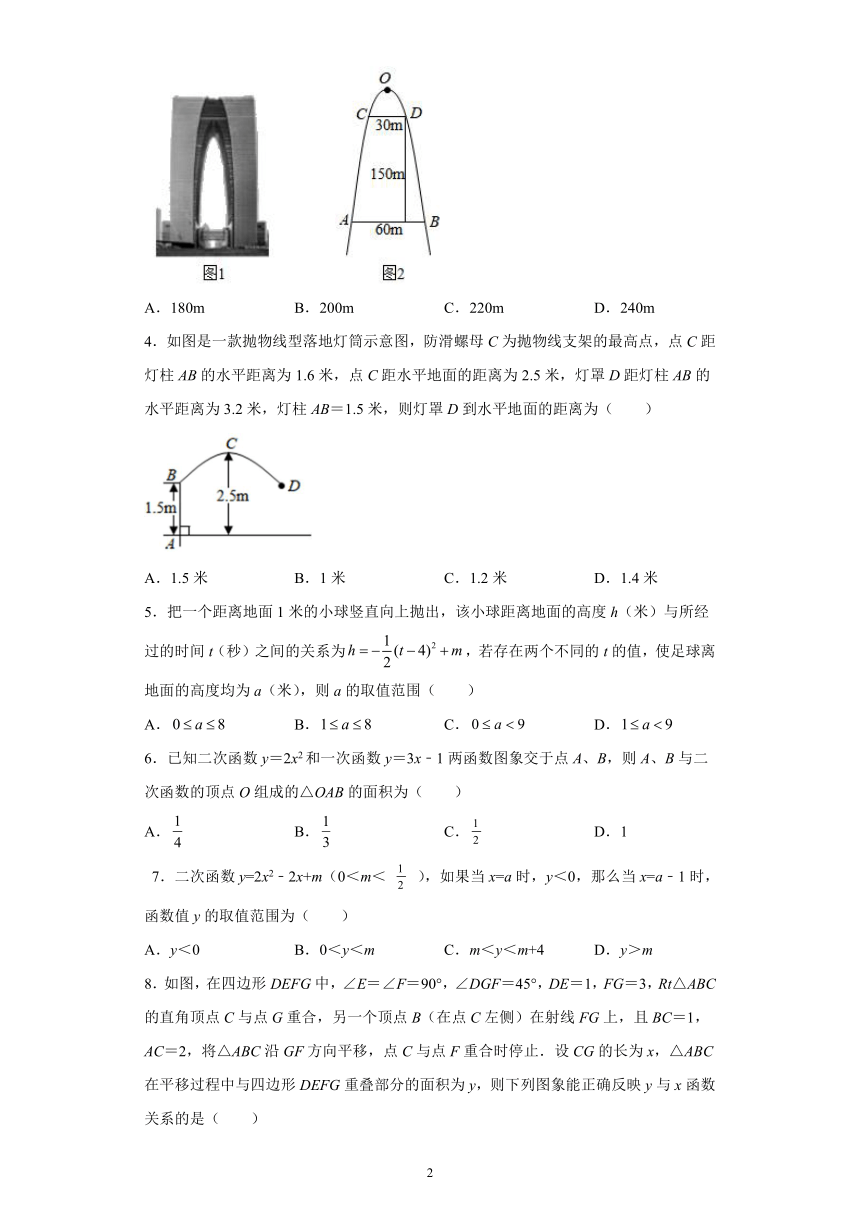
1.在平面直角坐标系中,对图形给出如下定义:若图形上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,如图中的矩形的坐标角度是90°.现将二次函数的图象在直线下方的部分沿直线向上:翻折,则所得图形的坐标角度的取值范围是(
)
A.
B.
C.
D.
2.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长.小明认为:隔离区的最大面积为;小亮认为:隔离区的面积可能为,则(
)
A.小明正确,小亮错误
B.小明错误,小亮正确
C.两人均正确
D.两人均错误
3.苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长60m的连桥连接,在该抛物线两侧距连桥150m处各有一窗户,两窗户的水平距离为30m,如图2,则此抛物线顶端O到连桥AB距离为(
)
A.180m
B.200m
C.220m
D.240m
4.如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,点C距灯柱AB的水平距离为1.6米,点C距水平地面的距离为2.5米,灯罩D距灯柱AB的水平距离为3.2米,灯柱AB=1.5米,则灯罩D到水平地面的距离为(
)
A.1.5米
B.1米
C.1.2米
D.1.4米
5.把一个距离地面1米的小球竖直向上抛出,该小球距离地面的高度h(米)与所经过的时间t(秒)之间的关系为,若存在两个不同的t的值,使足球离地面的高度均为a(米),则a的取值范围(
)
A.
B.
C.
D.
6.已知二次函数y=2x2和一次函数y=3x﹣1两函数图象交于点A、B,则A、B与二次函数的顶点O组成的△OAB的面积为( )
A.
B.
C.
D.1
7.二次函数y=2x2﹣2x+m(0<m<
),如果当x=a时,y<0,那么当x=a﹣1时,函数值y的取值范围为( )
A.y<0
B.0<y<m
C.m<y<m+4
D.y>m
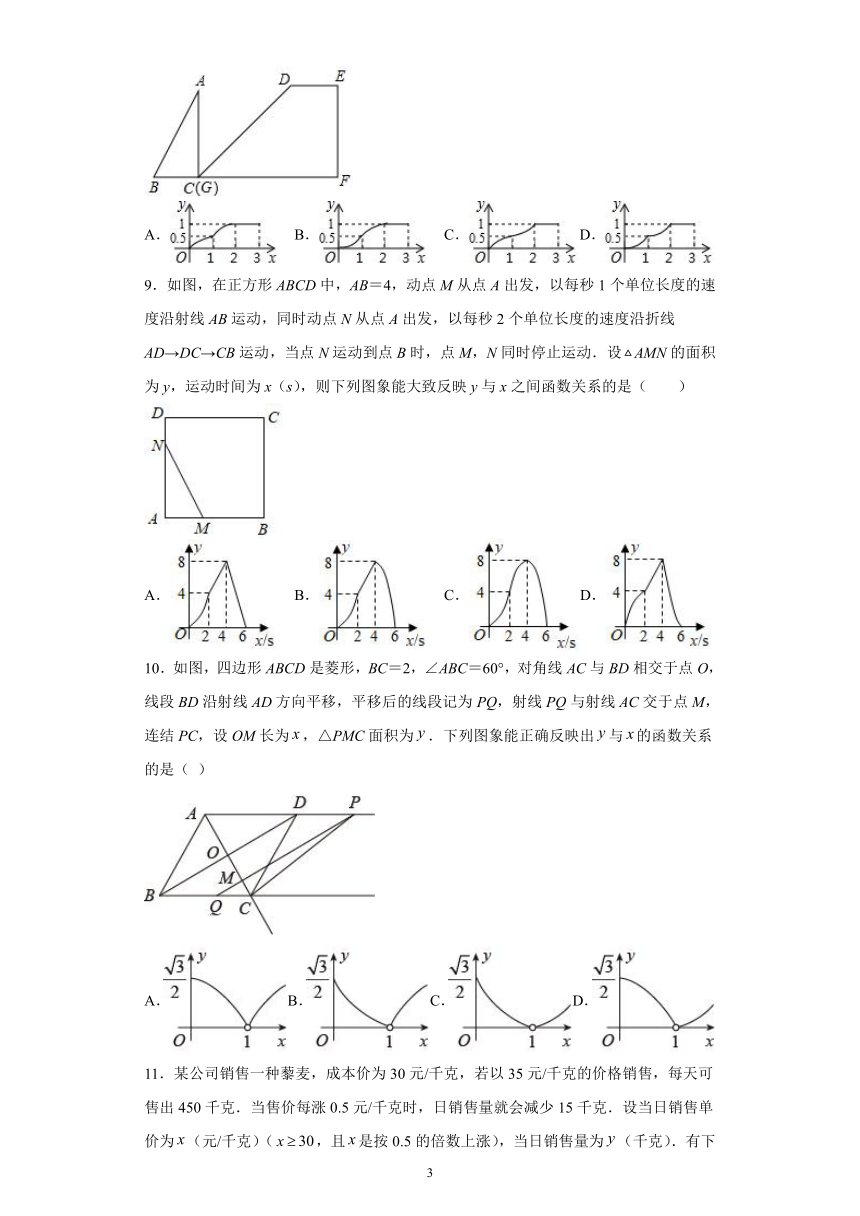
8.如图,在四边形DEFG中,∠E=∠F=90°,∠DGF=45°,DE=1,FG=3,Rt△ABC的直角顶点C与点G重合,另一个顶点B(在点C左侧)在射线FG上,且BC=1,AC=2,将△ABC沿GF方向平移,点C与点F重合时停止.设CG的长为x,△ABC在平移过程中与四边形DEFG重叠部分的面积为y,则下列图象能正确反映y与x函数关系的是(
)
A.
B.
C.D.
9.如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M,N同时停止运动.设AMN的面积为y,运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是(
)
A.
B.
C.D.
10.如图,四边形ABCD是菱形,BC=2,∠ABC=60°,对角线AC与BD相交于点O,线段BD沿射线AD方向平移,平移后的线段记为PQ,射线PQ与射线AC交于点M,连结PC,设OM长为,△PMC面积为.下列图象能正确反映出与的函数关系的是(
)
A.B.C.D.
11.某公司销售一种藜麦,成本价为30元/千克,若以35元/千克的价格销售,每天可售出450千克.当售价每涨0.5元/千克时,日销售量就会减少15千克.设当日销售单价为(元/千克)(,且是按0.5的倍数上涨),当日销售量为(千克).有下列说法:
①当时,
②与之间的函数关系式为
③若使日销售利润为2880元,且销售量较大,则日销售单价应定为42元/千克
④若使日销售利润最大,销售价格应定为40元/千克
其中正确的是(
)
A.①②
B.①②④
C.①②③
D.②④
12.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t=;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③
B.①②③
C.①②③④
D.②③④
13.如图,在矩形ABCD中,AD=8
cm,AB=6
cm.动点E从点C开始沿边CB向终点B以2
cm/s的速度运动,同时动点F从点C出发沿边CD向点D以1
cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是(
)
A.
B.
C.
D.
14.如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3…如此变换进行下去,若点P(21,m)在这种连续变换的图象上,则m的值为( )
A.2
B.﹣2
C.﹣3
D.3
二、填空题
15.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是,飞机着陆至停下来期间的最后10
s共滑行_______________m.
16.汽车刹车后行驶的距离s(米)与行驶时间t(秒)的函数关系是,汽车从刹车到停下来所用时间是___________秒.
17.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
18.如图,用一段长为10米的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园,设为米,则菜园的面积(平方米)与(米)的关系式为______.(不要求写出自变量的取值范围)
19.在“乡村振兴”行动中,某村办企业以,两种农作物为原料开发了一种有机产品.原料的单价是原料单价的倍,若用元收购原料会比用元收购原料少.生产该产品每盒需要原料和原料,盒还需其他成本元.市场调查发现:该产品每盒的售价是元时,每天可以销售盒;每涨价元,每天少销售盒.
(1)填空:、两原料的单价分别为____元、_____元,每盒产品的成本______元(成本=原料费+其他成本)
(2)设每盒产品的售价是元(是整数),每天的利润是元,求关于的函数解析式(不需要写出自变量的取值范围);
(3)若每盒产品的售价不超过元(是大于的常数且是整数),直接写出每天的最大利润.
三、解答题
20.如图1,抛物线与轴交于,两点,与轴交于点,,矩形的边,延长交抛物线于点.
(1)求抛物线的解析式.
(2)如图2,点是直线上方抛物线上的一个动点,过点作轴的平行线交直线于点,作,垂足为.设的长为,点的横坐标为,求与的函数关系式(不必写出的取值范围),并求出的最大值.
(3)如果点是抛物线对称轴上的一点,抛物线上是否存在点,使得以,,,为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由.
21.某家电生产厂家去年销往农村的某品牌洗碗机每台的售价(元)与月份之间满足函数关系,年的月销售量(万台)与月份之间成一次函数关系,其中两个月的销售情况如下表:
月份
1月
5月
销量
3.9万台
4.3万台
求该品牌洗碗机在去年哪个月销往农村的销售金额最大?最大是多少?
22.如图,在平面直角坐标系中,抛物线W1:y=x2+bx+c与x轴交于A(﹣4,0)、B两点,且过点C(0,﹣2).抛物线W2与抛物线W1关于原点对称,点C在W2上的对应点为C′.
(1)求抛物线W1的表达式;
(2)写出抛物线W2的表达式;
(3)若点P在抛物线W1上,试探究:在抛物线W2上是否存在点Q,使以C、C′、P、Q为顶点的四边形是平行四边形,并且其面积等于24?若存在,求点Q的坐标;若不存在,请说明理由.
参考答案
1.D
解:当a=1时,如图1所示,
∵角两边分别过点A(-1,1),B(1,1),
作BE⊥x轴于点E,
∴BE=OE,
∴∠BOE=45°,
根据对称性可知:∠AOB=90°,
∴此时坐标角度=90°;
当a=3时,如图2所示,
角两边分别过点A(,1),B(,1),
作BE⊥x轴于点E,
∵,
∴∠BOE=60°,
根据对称性可知:∠AOB=60°,
∴此时坐标角度=90°,
∴60°≤≤90°,
故选:D.
2.B
解:设隔离区靠近墙的长度为x
m(0<x≤5),隔离区的面积为S
m2,由题意得:
=,
∴对称轴为x=,
∵0<x≤5,抛物线开口向下,在对称轴左侧,S随x的增大而增大,
∴当x=5时,S有最大值:
Smax=
∵9<<12,
∴小明错误;
令S=9得:9=,
解得:x1=9(舍),x2=3,
∴x=3时,S=9.
∴隔离区的面积可能为9m2.
故选:B.
3.B
解:以所在的直线为轴,以线段的垂直平分线所在的直线为轴建立平面直角坐标系:
,,,
设抛物线的解析式为,将代入,得:
,
解得:,
,
抛物线顶端的坐标为,
此抛物线顶端到连桥距离为.
故选:B.
4.A
解:由题意可得,
点C为抛物线的最高点,即抛物线的顶点,
∵点C距灯柱AB的水平距离为1.6米,灯罩D距灯柱AB的水平距离为3.2米,
∴点B和点D关于点C所在的直线对称,
∵灯柱AB=1.5米,
∴灯罩D到水平地面的距离为1.5米,
故选:A.
5.D
解:将(0,1)代入,得:
,
解得:,
∴,
令,则可得方程,
∵存在两个不同的的值,使足球离地面的高度均为,
∴方程有两个不相等的实根,
整理得:,
△,
解得:,
又,
∴的取值范围为:,
故选:D.
6.A
解:联立,
解得x1=1,x2=,
∴A、B的坐标为(,),(1,2),
∴S△OAB=S△OBC﹣S△ABD﹣S梯形OADC=×1×2﹣××﹣×(+1)×=.
故选:A.
7.C
解:画出草图,
∵0<m<
,∴△=4﹣8m>0,
∵对称轴为x=
,x=0或1时,y=m>0,
∴当y<0时,0<a<1,
∴-1<a-1<0,
∵当x=-1时,y=2+2+m=4+m,
??
当x=0时,y=8﹣4+m=m,
∴当x=a-1时,函数值y的取值范围为m<y<m+4,
故答案为:
C.
8.B
解:过点D作DH⊥EF,
∵∠DGF=45°,DE=1,FG=3,
∴EH=2,DH=EF=2,
当0<x<1时,重叠部分为等腰直角三角形,且直角边长为x,
∴y=,
∵,
∴该部分图象开口向上,
当1<x<2时,如图,
设A'B'与DG交与点N,A'C'与DG交与点M,
则S重叠=S△GMC'﹣S△GNB',
设B'K=a,则NK=2a,
∵GC'=x,B'C'=1,
∴GB'=x﹣1,
∵△GKN是等腰直角三角形,
∴GK=NK,
∴x﹣1+a=2a,
∴a=x﹣1,
∴NK=2x﹣2,
∴,
∵,
∴S重叠=﹣(x2﹣2x+1)=,
∵,
∴该部分图象开口向下,
当2<x<3时,重叠部分的面积为S△ABC,是固定值,
∴该部分图象是平行x轴的线段,
故选:B.
9.B
解:当点N在AD上时,即0≤x<2
∵AM=x,AN=2x,
∴,
此时二次项系数大于0,
∴该部分函数图象开口向上,
当点N在DC上时,即2≤x<4,
此时底边AM=x,高AD=4,
∴y==2x,
∴该部分图象为直线段,
当点N在CB上时,即4≤x<6时,
此时底边AM=x,高BN=12﹣2x,
∴y=,
∵﹣1<0,
∴该部分函数图象开口向下,
故选:B.
10.D
解:∵四边形ABCD是菱形,
∴AD=BC=2,∠BAD=180°?∠ABC=120°,
∴∠DAO=∠BAD=60°,
∴△DAC是等边三角形,
∴AD=AC=2,
∴AO=CO=AC=1,
设OM=x,
∵AC⊥BD,PQ为BD平移而来,
∴∠AOD=∠AMP=90°,
∴△AMP为直角三角形,
∴PM=AM?tan∠PAM=(1+x),
①当点M在线段OC上(不含点O)时,
即0≤x<1,此时CM=1?x,
则y=(1?x)×(1+x)=?,
∴0≤x<1,函数图象开口应朝下,
故B、C不符合题意,
②当点在线段OC延长线上时,即x>1,如图所示:
此时C=x?1,
则y=(x?1)×(x+1)=,
∴只有D选项符合题意,
故选:D.
11.B
当时,,故①正确;
由题意得:,故②正确;
日销售利润为,
由题意得:,
整理得:,
解得:,,
∵销售单价为38元/千克时的销售量比销售单价为42元/千克时大,
∴不合题意,
即若使日销售利润为2880元,且销售量较大,则日销售单价应定为38元/千克,故③错误;
由上问可知:,
即,
∵,
∴当时,,
即若使日销售利润最大,销售价格应定为40元/千克,故④正确;
故正确的是①②④;
故答案选B.
12.C
解:由题意,抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
∴h=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m>20m,故①正确,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,h=0,
∴点(9,0)在该抛物线上,故③正确,
∵当t=5时,h=20,当t=7时,h=14,
∴足球被踢出5s~7s时,距离地面的高度逐渐下降,故④正确.
∴正确的有①②③④,
故选:C.
13.A
解:此题在读懂题意的基础上,分两种情况讨论:
当x≤4时,y=6×8?(x?2x)=?2x2+48,
此时函数的图象为抛物线的一部分,
它的最上点抛物线的顶点(0,48),最下点为(4,16);
当4<x≤6时,点E停留在B点处,
故y=48?8x=?8x+48,此时函数的图象为直线y=?8x+48的一部分,
它的最上点可以为(4,16),它的最下点为(6,0).
结合四个选项的图象知选A项.
故选:A.
14.C
解:∵y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1,
∴点A1(4,0),
∴OA1=4,
∵OA1=A1A2=A2A3=A3A4,
∴OA1=A1A2=A2A3=A3A4=4,
∵点P(21,m)在这种连续变换的图象上,
∴x=21和x=1时的函数值互为相反数,
∴﹣m=﹣1×(1﹣4)=3,
∴m=﹣3,
故选:C.
15.
解:∵,
∴当t=25时,y取得最大值750,
即飞机着陆后滑行750米才能停下来,
因此t的取值范围是0≤t≤25;
即当t=15时,y=630,
所以最后10s共滑行750?630=120(米)
故答案是:120.
16.1.5
解:∵s=18t-6t2,=-6(t-1.5)2+13.5,
∴当t=1.5秒时,s取得最大值,即汽车停下来.
故答案为:1.5
17.11
解:设销售单价定为元,每天所获利润为元,
则
,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
故答案为11.
18.y=-2x2+10x
解:∵AB的边长为x米,而菜园ABCD是矩形菜园,
∴BC=10-2x,
∵菜园的面积=AB×BC=x?(10-2x),
∴y=-2x2+10x.
故答案为:y=-2x2+10x.
19.(1)4.5,
3,
30
(2)w=?10x2+1400x?33000;(3)当a≥70时,每天最大利润为16000元,当60<a<70时,每天的最大利润为(?10a2+1400a?33000)元.
解:(1)设B原料单价为m元,则A原料单价为1.5m元,
根据题意,得:,解得m=3,
经检验m=3是方程的解,
∴1.5m=4.5,
∴每盒产品的成本是:4.5×2+4×3+9=30(元),
故答案是:4.5,3,30;
(2)根据题意,得w=(x?30)[500?10(x?60)]=?10x2+1400x?33000,
∴w关于x的函数解析式为:w=?10x2+1400x?33000;
(3)由(2)知w=?10x2+1400x?33000=?10(x?70)2+16000,
∴当a≥70时,每天最大利润为16000元,
当60<a<70时,每天的最大利润为(?10a2+1400a?33000)元.
20.(1).(2),当时,有最大值,最大值为.(3)存在,或或.
(1)∵矩形的边,
∴,
∵,
∴,
∴,,
把、两点坐标代入抛物线解析式可得,解得,
∴抛物线解析式为.
(2)在中,
令,可得,解得或,
∴,
∴直线解析式为,
由题意可得,
∵轴,
∴,
∵在直线的上方,
∴,
∵直线解析式为,
∴,
∴,
∴当时,有最大值,最大值为.
(3)①当为平行四边形的边时,则有,且,
如图,过作对称轴的垂线,垂足为,
设交对称轴于点,则,
在和中,,
∴≌(AAS),
∴,
∴点到对称轴的距离为3,
又,
∴抛物线对称轴为,
设点坐标为,则,解得或,
当时,;当时,,
∴点坐标为或.
②当为对角线时,设的中点为,
∵,,
∴,
∵点在对称轴上,
∴点的横坐标为,
设点横坐标为,
∴,解得,此时,
∴.
综上可知点的坐标为或或.
21.该品牌洗碗机在去年7月销往农村的销售金额最大,最大是10125万元.
解:设p与x的函数关系式为p=kx+b(k≠0),
根据题意,得
解得:
∴p=0.1x+3.8,
设月销售金额为w万元,
则w=py=(0.1x+3.8)(-50x+2600),
=-5x2+70x+9880
=-5(x-7)2+10125,
当x=7时,w取得最大值为10125.
答:该品牌洗碗机在去年7月销往农村的销售金额最大,最大是10125万元.
22.(1)y=;(2)y=;(3)存在,Q点坐标为(﹣6,10)或(6,﹣4).
解(1)把点A、点C的坐标分别代入y=x2+bx+c中,
得:,
∴b=,c=-2,
∴y=;
(2)∵抛物线w1:y==(x+1)2﹣的顶点是(﹣1,﹣),
∴w2的顶点是(1,),
∴w2的解析式是:y=﹣(x﹣1)2+=﹣x2+x+2;
(3)存在.
由题意知,,则.
①若CC′是对角线,如图,
∵W1和W2关于原点对称,
∴P、Q也关于原点对称,
设点P到y轴的距离为h,
∵平行四边形的面积=2
∴CC′?h=24,
∴4?h=24,
∴h=6,
即P点横坐标是6或﹣6,
当x=6时,y=×62+×6﹣2=10,
∴Q(﹣6,10),
当x=﹣6时,y=×(﹣6)2﹣×6﹣2=4,
∴Q(6,﹣4),
②当CC′是边时,PQ∥CC′,PQ=CC′,如图,
设点Q(x,),P(x,),
由①知:x=6或﹣6,
当P(6,10)时,
∵y=﹣×62+×6+2=﹣4,
∴Q(6,﹣4),
∴PQ=14≠4,
当x=﹣6时,y=﹣×(﹣6)2+×(﹣6)+2=﹣10,
∴PQ=14,
∴PQ≠CC′,
∴CC′不能为边,
综上所述,当C、C′、P、Q为顶点的四边形是平行四边形,并且其面积等于24时,点Q的坐标是(﹣6,10)或(6,﹣4).
二次函数的应用
一、单选题
1.在平面直角坐标系中,对图形给出如下定义:若图形上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,如图中的矩形的坐标角度是90°.现将二次函数的图象在直线下方的部分沿直线向上:翻折,则所得图形的坐标角度的取值范围是(
)
A.
B.
C.
D.
2.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为,如果隔离区出入口的大小不计,并且隔离区靠墙的一面不能超过墙长.小明认为:隔离区的最大面积为;小亮认为:隔离区的面积可能为,则(
)
A.小明正确,小亮错误
B.小明错误,小亮正确
C.两人均正确
D.两人均错误
3.苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长60m的连桥连接,在该抛物线两侧距连桥150m处各有一窗户,两窗户的水平距离为30m,如图2,则此抛物线顶端O到连桥AB距离为(
)
A.180m
B.200m
C.220m
D.240m
4.如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,点C距灯柱AB的水平距离为1.6米,点C距水平地面的距离为2.5米,灯罩D距灯柱AB的水平距离为3.2米,灯柱AB=1.5米,则灯罩D到水平地面的距离为(
)
A.1.5米
B.1米
C.1.2米
D.1.4米
5.把一个距离地面1米的小球竖直向上抛出,该小球距离地面的高度h(米)与所经过的时间t(秒)之间的关系为,若存在两个不同的t的值,使足球离地面的高度均为a(米),则a的取值范围(
)
A.
B.
C.
D.
6.已知二次函数y=2x2和一次函数y=3x﹣1两函数图象交于点A、B,则A、B与二次函数的顶点O组成的△OAB的面积为( )
A.
B.
C.
D.1
7.二次函数y=2x2﹣2x+m(0<m<
),如果当x=a时,y<0,那么当x=a﹣1时,函数值y的取值范围为( )
A.y<0
B.0<y<m
C.m<y<m+4
D.y>m
8.如图,在四边形DEFG中,∠E=∠F=90°,∠DGF=45°,DE=1,FG=3,Rt△ABC的直角顶点C与点G重合,另一个顶点B(在点C左侧)在射线FG上,且BC=1,AC=2,将△ABC沿GF方向平移,点C与点F重合时停止.设CG的长为x,△ABC在平移过程中与四边形DEFG重叠部分的面积为y,则下列图象能正确反映y与x函数关系的是(
)
A.
B.
C.D.
9.如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M,N同时停止运动.设AMN的面积为y,运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是(
)
A.
B.
C.D.
10.如图,四边形ABCD是菱形,BC=2,∠ABC=60°,对角线AC与BD相交于点O,线段BD沿射线AD方向平移,平移后的线段记为PQ,射线PQ与射线AC交于点M,连结PC,设OM长为,△PMC面积为.下列图象能正确反映出与的函数关系的是(
)
A.B.C.D.
11.某公司销售一种藜麦,成本价为30元/千克,若以35元/千克的价格销售,每天可售出450千克.当售价每涨0.5元/千克时,日销售量就会减少15千克.设当日销售单价为(元/千克)(,且是按0.5的倍数上涨),当日销售量为(千克).有下列说法:
①当时,
②与之间的函数关系式为
③若使日销售利润为2880元,且销售量较大,则日销售单价应定为42元/千克
④若使日销售利润最大,销售价格应定为40元/千克
其中正确的是(
)
A.①②
B.①②④
C.①②③
D.②④
12.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t=;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
A.②③
B.①②③
C.①②③④
D.②③④
13.如图,在矩形ABCD中,AD=8
cm,AB=6
cm.动点E从点C开始沿边CB向终点B以2
cm/s的速度运动,同时动点F从点C出发沿边CD向点D以1
cm/s的速度运动至点D停止.如图可得到矩形CFHE,设运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是(
)
A.
B.
C.
D.
14.如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3…如此变换进行下去,若点P(21,m)在这种连续变换的图象上,则m的值为( )
A.2
B.﹣2
C.﹣3
D.3
二、填空题
15.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是,飞机着陆至停下来期间的最后10
s共滑行_______________m.
16.汽车刹车后行驶的距离s(米)与行驶时间t(秒)的函数关系是,汽车从刹车到停下来所用时间是___________秒.
17.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
18.如图,用一段长为10米的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园,设为米,则菜园的面积(平方米)与(米)的关系式为______.(不要求写出自变量的取值范围)
19.在“乡村振兴”行动中,某村办企业以,两种农作物为原料开发了一种有机产品.原料的单价是原料单价的倍,若用元收购原料会比用元收购原料少.生产该产品每盒需要原料和原料,盒还需其他成本元.市场调查发现:该产品每盒的售价是元时,每天可以销售盒;每涨价元,每天少销售盒.
(1)填空:、两原料的单价分别为____元、_____元,每盒产品的成本______元(成本=原料费+其他成本)
(2)设每盒产品的售价是元(是整数),每天的利润是元,求关于的函数解析式(不需要写出自变量的取值范围);
(3)若每盒产品的售价不超过元(是大于的常数且是整数),直接写出每天的最大利润.
三、解答题
20.如图1,抛物线与轴交于,两点,与轴交于点,,矩形的边,延长交抛物线于点.
(1)求抛物线的解析式.
(2)如图2,点是直线上方抛物线上的一个动点,过点作轴的平行线交直线于点,作,垂足为.设的长为,点的横坐标为,求与的函数关系式(不必写出的取值范围),并求出的最大值.
(3)如果点是抛物线对称轴上的一点,抛物线上是否存在点,使得以,,,为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由.
21.某家电生产厂家去年销往农村的某品牌洗碗机每台的售价(元)与月份之间满足函数关系,年的月销售量(万台)与月份之间成一次函数关系,其中两个月的销售情况如下表:
月份
1月
5月
销量
3.9万台
4.3万台
求该品牌洗碗机在去年哪个月销往农村的销售金额最大?最大是多少?
22.如图,在平面直角坐标系中,抛物线W1:y=x2+bx+c与x轴交于A(﹣4,0)、B两点,且过点C(0,﹣2).抛物线W2与抛物线W1关于原点对称,点C在W2上的对应点为C′.
(1)求抛物线W1的表达式;
(2)写出抛物线W2的表达式;
(3)若点P在抛物线W1上,试探究:在抛物线W2上是否存在点Q,使以C、C′、P、Q为顶点的四边形是平行四边形,并且其面积等于24?若存在,求点Q的坐标;若不存在,请说明理由.
参考答案
1.D
解:当a=1时,如图1所示,
∵角两边分别过点A(-1,1),B(1,1),
作BE⊥x轴于点E,
∴BE=OE,
∴∠BOE=45°,
根据对称性可知:∠AOB=90°,
∴此时坐标角度=90°;
当a=3时,如图2所示,
角两边分别过点A(,1),B(,1),
作BE⊥x轴于点E,
∵,
∴∠BOE=60°,
根据对称性可知:∠AOB=60°,
∴此时坐标角度=90°,
∴60°≤≤90°,
故选:D.
2.B
解:设隔离区靠近墙的长度为x
m(0<x≤5),隔离区的面积为S
m2,由题意得:
=,
∴对称轴为x=,
∵0<x≤5,抛物线开口向下,在对称轴左侧,S随x的增大而增大,
∴当x=5时,S有最大值:
Smax=
∵9<<12,
∴小明错误;
令S=9得:9=,
解得:x1=9(舍),x2=3,
∴x=3时,S=9.
∴隔离区的面积可能为9m2.
故选:B.
3.B
解:以所在的直线为轴,以线段的垂直平分线所在的直线为轴建立平面直角坐标系:
,,,
设抛物线的解析式为,将代入,得:
,
解得:,
,
抛物线顶端的坐标为,
此抛物线顶端到连桥距离为.
故选:B.
4.A
解:由题意可得,
点C为抛物线的最高点,即抛物线的顶点,
∵点C距灯柱AB的水平距离为1.6米,灯罩D距灯柱AB的水平距离为3.2米,
∴点B和点D关于点C所在的直线对称,
∵灯柱AB=1.5米,
∴灯罩D到水平地面的距离为1.5米,
故选:A.
5.D
解:将(0,1)代入,得:
,
解得:,
∴,
令,则可得方程,
∵存在两个不同的的值,使足球离地面的高度均为,
∴方程有两个不相等的实根,
整理得:,
△,
解得:,
又,
∴的取值范围为:,
故选:D.
6.A
解:联立,
解得x1=1,x2=,
∴A、B的坐标为(,),(1,2),
∴S△OAB=S△OBC﹣S△ABD﹣S梯形OADC=×1×2﹣××﹣×(+1)×=.
故选:A.
7.C
解:画出草图,
∵0<m<
,∴△=4﹣8m>0,
∵对称轴为x=
,x=0或1时,y=m>0,
∴当y<0时,0<a<1,
∴-1<a-1<0,
∵当x=-1时,y=2+2+m=4+m,
??
当x=0时,y=8﹣4+m=m,
∴当x=a-1时,函数值y的取值范围为m<y<m+4,
故答案为:
C.
8.B
解:过点D作DH⊥EF,
∵∠DGF=45°,DE=1,FG=3,
∴EH=2,DH=EF=2,
当0<x<1时,重叠部分为等腰直角三角形,且直角边长为x,
∴y=,
∵,
∴该部分图象开口向上,
当1<x<2时,如图,
设A'B'与DG交与点N,A'C'与DG交与点M,
则S重叠=S△GMC'﹣S△GNB',
设B'K=a,则NK=2a,
∵GC'=x,B'C'=1,
∴GB'=x﹣1,
∵△GKN是等腰直角三角形,
∴GK=NK,
∴x﹣1+a=2a,
∴a=x﹣1,
∴NK=2x﹣2,
∴,
∵,
∴S重叠=﹣(x2﹣2x+1)=,
∵,
∴该部分图象开口向下,
当2<x<3时,重叠部分的面积为S△ABC,是固定值,
∴该部分图象是平行x轴的线段,
故选:B.
9.B
解:当点N在AD上时,即0≤x<2
∵AM=x,AN=2x,
∴,
此时二次项系数大于0,
∴该部分函数图象开口向上,
当点N在DC上时,即2≤x<4,
此时底边AM=x,高AD=4,
∴y==2x,
∴该部分图象为直线段,
当点N在CB上时,即4≤x<6时,
此时底边AM=x,高BN=12﹣2x,
∴y=,
∵﹣1<0,
∴该部分函数图象开口向下,
故选:B.
10.D
解:∵四边形ABCD是菱形,
∴AD=BC=2,∠BAD=180°?∠ABC=120°,
∴∠DAO=∠BAD=60°,
∴△DAC是等边三角形,
∴AD=AC=2,
∴AO=CO=AC=1,
设OM=x,
∵AC⊥BD,PQ为BD平移而来,
∴∠AOD=∠AMP=90°,
∴△AMP为直角三角形,
∴PM=AM?tan∠PAM=(1+x),
①当点M在线段OC上(不含点O)时,
即0≤x<1,此时CM=1?x,
则y=(1?x)×(1+x)=?,
∴0≤x<1,函数图象开口应朝下,
故B、C不符合题意,
②当点在线段OC延长线上时,即x>1,如图所示:
此时C=x?1,
则y=(x?1)×(x+1)=,
∴只有D选项符合题意,
故选:D.
11.B
当时,,故①正确;
由题意得:,故②正确;
日销售利润为,
由题意得:,
整理得:,
解得:,,
∵销售单价为38元/千克时的销售量比销售单价为42元/千克时大,
∴不合题意,
即若使日销售利润为2880元,且销售量较大,则日销售单价应定为38元/千克,故③错误;
由上问可知:,
即,
∵,
∴当时,,
即若使日销售利润最大,销售价格应定为40元/千克,故④正确;
故正确的是①②④;
故答案选B.
12.C
解:由题意,抛物线的解析式为h=at(t﹣9),把(1,8)代入可得a=﹣1,
∴h=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m>20m,故①正确,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,h=0,
∴点(9,0)在该抛物线上,故③正确,
∵当t=5时,h=20,当t=7时,h=14,
∴足球被踢出5s~7s时,距离地面的高度逐渐下降,故④正确.
∴正确的有①②③④,
故选:C.
13.A
解:此题在读懂题意的基础上,分两种情况讨论:
当x≤4时,y=6×8?(x?2x)=?2x2+48,
此时函数的图象为抛物线的一部分,
它的最上点抛物线的顶点(0,48),最下点为(4,16);
当4<x≤6时,点E停留在B点处,
故y=48?8x=?8x+48,此时函数的图象为直线y=?8x+48的一部分,
它的最上点可以为(4,16),它的最下点为(6,0).
结合四个选项的图象知选A项.
故选:A.
14.C
解:∵y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1,
∴点A1(4,0),
∴OA1=4,
∵OA1=A1A2=A2A3=A3A4,
∴OA1=A1A2=A2A3=A3A4=4,
∵点P(21,m)在这种连续变换的图象上,
∴x=21和x=1时的函数值互为相反数,
∴﹣m=﹣1×(1﹣4)=3,
∴m=﹣3,
故选:C.
15.
解:∵,
∴当t=25时,y取得最大值750,
即飞机着陆后滑行750米才能停下来,
因此t的取值范围是0≤t≤25;
即当t=15时,y=630,
所以最后10s共滑行750?630=120(米)
故答案是:120.
16.1.5
解:∵s=18t-6t2,=-6(t-1.5)2+13.5,
∴当t=1.5秒时,s取得最大值,即汽车停下来.
故答案为:1.5
17.11
解:设销售单价定为元,每天所获利润为元,
则
,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
故答案为11.
18.y=-2x2+10x
解:∵AB的边长为x米,而菜园ABCD是矩形菜园,
∴BC=10-2x,
∵菜园的面积=AB×BC=x?(10-2x),
∴y=-2x2+10x.
故答案为:y=-2x2+10x.
19.(1)4.5,
3,
30
(2)w=?10x2+1400x?33000;(3)当a≥70时,每天最大利润为16000元,当60<a<70时,每天的最大利润为(?10a2+1400a?33000)元.
解:(1)设B原料单价为m元,则A原料单价为1.5m元,
根据题意,得:,解得m=3,
经检验m=3是方程的解,
∴1.5m=4.5,
∴每盒产品的成本是:4.5×2+4×3+9=30(元),
故答案是:4.5,3,30;
(2)根据题意,得w=(x?30)[500?10(x?60)]=?10x2+1400x?33000,
∴w关于x的函数解析式为:w=?10x2+1400x?33000;
(3)由(2)知w=?10x2+1400x?33000=?10(x?70)2+16000,
∴当a≥70时,每天最大利润为16000元,
当60<a<70时,每天的最大利润为(?10a2+1400a?33000)元.
20.(1).(2),当时,有最大值,最大值为.(3)存在,或或.
(1)∵矩形的边,
∴,
∵,
∴,
∴,,
把、两点坐标代入抛物线解析式可得,解得,
∴抛物线解析式为.
(2)在中,
令,可得,解得或,
∴,
∴直线解析式为,
由题意可得,
∵轴,
∴,
∵在直线的上方,
∴,
∵直线解析式为,
∴,
∴,
∴当时,有最大值,最大值为.
(3)①当为平行四边形的边时,则有,且,
如图,过作对称轴的垂线,垂足为,
设交对称轴于点,则,
在和中,,
∴≌(AAS),
∴,
∴点到对称轴的距离为3,
又,
∴抛物线对称轴为,
设点坐标为,则,解得或,
当时,;当时,,
∴点坐标为或.
②当为对角线时,设的中点为,
∵,,
∴,
∵点在对称轴上,
∴点的横坐标为,
设点横坐标为,
∴,解得,此时,
∴.
综上可知点的坐标为或或.
21.该品牌洗碗机在去年7月销往农村的销售金额最大,最大是10125万元.
解:设p与x的函数关系式为p=kx+b(k≠0),
根据题意,得
解得:
∴p=0.1x+3.8,
设月销售金额为w万元,
则w=py=(0.1x+3.8)(-50x+2600),
=-5x2+70x+9880
=-5(x-7)2+10125,
当x=7时,w取得最大值为10125.
答:该品牌洗碗机在去年7月销往农村的销售金额最大,最大是10125万元.
22.(1)y=;(2)y=;(3)存在,Q点坐标为(﹣6,10)或(6,﹣4).
解(1)把点A、点C的坐标分别代入y=x2+bx+c中,
得:,
∴b=,c=-2,
∴y=;
(2)∵抛物线w1:y==(x+1)2﹣的顶点是(﹣1,﹣),
∴w2的顶点是(1,),
∴w2的解析式是:y=﹣(x﹣1)2+=﹣x2+x+2;
(3)存在.
由题意知,,则.
①若CC′是对角线,如图,
∵W1和W2关于原点对称,
∴P、Q也关于原点对称,
设点P到y轴的距离为h,
∵平行四边形的面积=2
∴CC′?h=24,
∴4?h=24,
∴h=6,
即P点横坐标是6或﹣6,
当x=6时,y=×62+×6﹣2=10,
∴Q(﹣6,10),
当x=﹣6时,y=×(﹣6)2﹣×6﹣2=4,
∴Q(6,﹣4),
②当CC′是边时,PQ∥CC′,PQ=CC′,如图,
设点Q(x,),P(x,),
由①知:x=6或﹣6,
当P(6,10)时,
∵y=﹣×62+×6+2=﹣4,
∴Q(6,﹣4),
∴PQ=14≠4,
当x=﹣6时,y=﹣×(﹣6)2+×(﹣6)+2=﹣10,
∴PQ=14,
∴PQ≠CC′,
∴CC′不能为边,
综上所述,当C、C′、P、Q为顶点的四边形是平行四边形,并且其面积等于24时,点Q的坐标是(﹣6,10)或(6,﹣4).
同课章节目录
