2.3.1等腰三角形的性质定理 课件(共27张PPT)
文档属性
| 名称 | 2.3.1等腰三角形的性质定理 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-27 16:38:46 | ||
图片预览



文档简介
(共27张PPT)
2.3等腰三角形的性质定理
浙教版
八年级上
新知导入
将一把等腰三角尺和一个重锤如图1放置,就能检查一根讲台边沿是否水平,你知道为什么吗?
复习导入
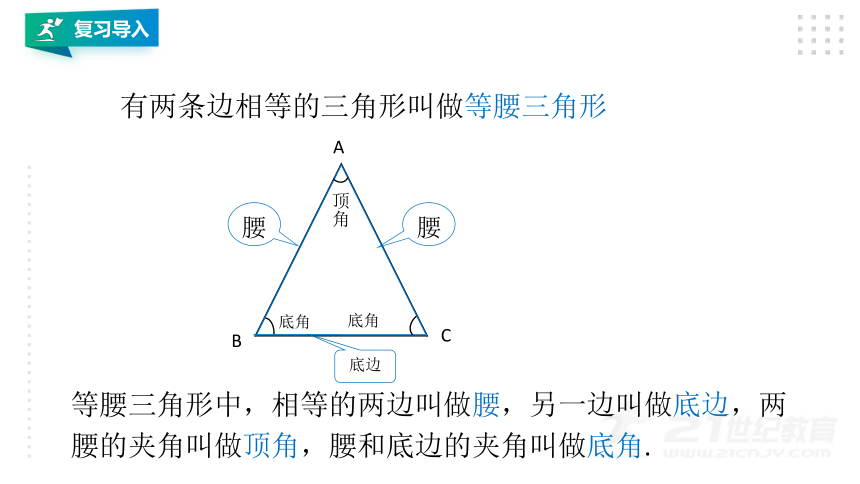
有两条边相等的三角形叫做等腰三角形
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
探究归纳
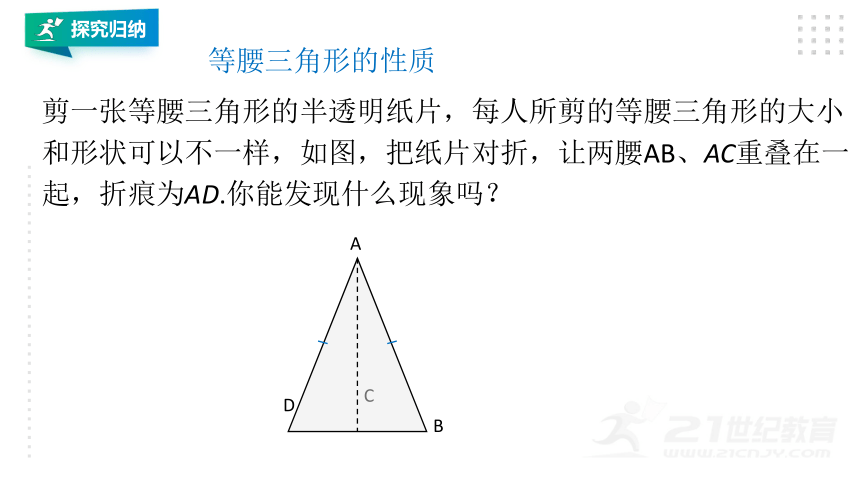
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
A
B
C
D
等腰三角形的性质
1.
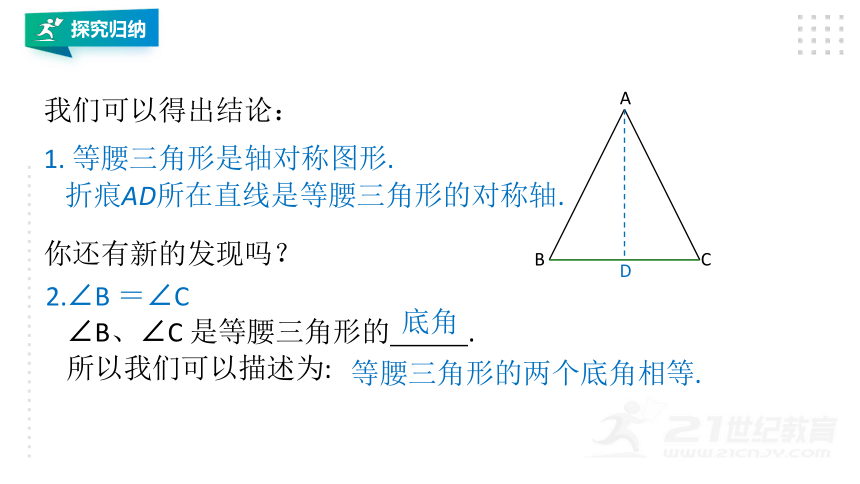
等腰三角形是轴对称图形.
我们可以得出结论:
A
C
B
D
折痕AD所在直线是等腰三角形的对称轴.
你还有新的发现吗?
∠B、∠C
是等腰三角形的
.
底角
∠B
=∠C
所以我们可以描述为:
等腰三角形的两个底角相等.
2.
探究归纳
等腰三角形的性质定理1:
等腰三角形的两个底角相等
(简写成“在同一个三角形中,
等边对等角”).
新知讲解
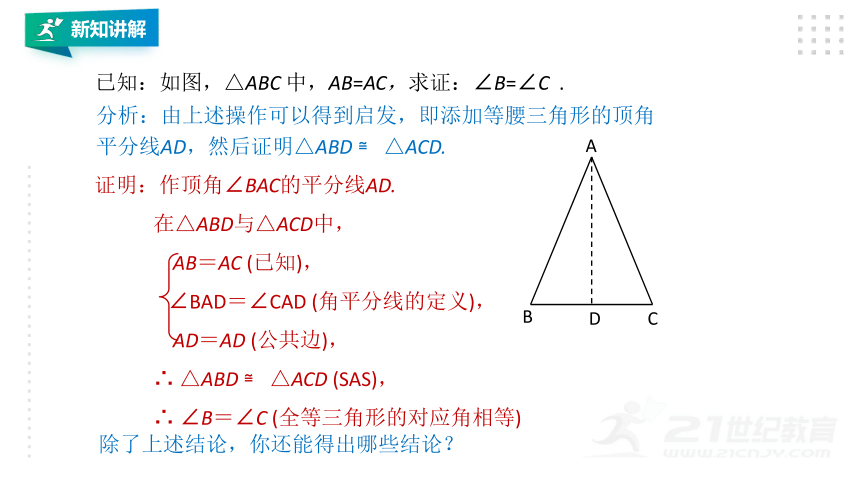
已知:如图,△ABC
中,AB=AC,求证:∠B=∠C
.
证明:作顶角∠BAC的平分线AD.
在△ABD与△ACD中,
AB=AC
(已知),
∠BAD=∠CAD
(角平分线的定义),
AD=AD
(公共边),
∴
△ABD
≌
△ACD
(SAS),
∴
∠B=∠C
(全等三角形的对应角相等)
A
B
C
分析:由上述操作可以得到启发,即添加等腰三角形的顶角平分线AD,然后证明△ABD
≌
△ACD.
D
除了上述结论,你还能得出哪些结论?
新知讲解
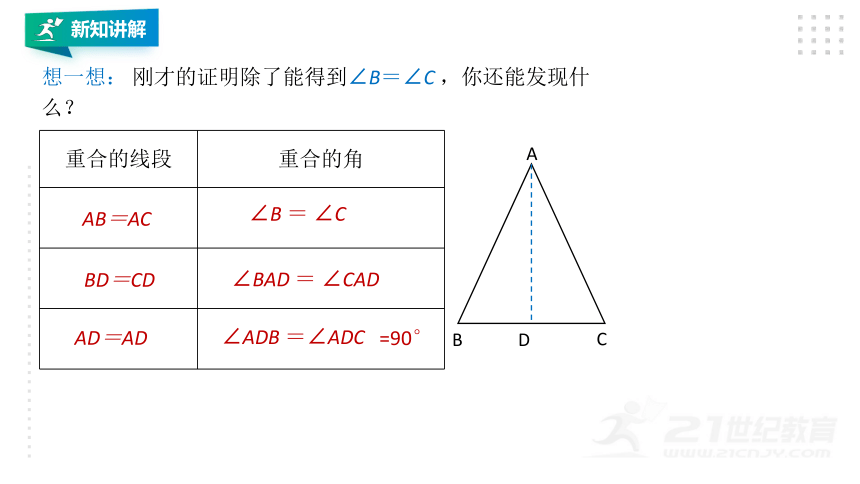
想一想:
刚才的证明除了能得到∠B=∠C
,你还能发现什么?
重合的线段
重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B
=
∠C
∠BAD
=
∠CAD
∠ADB
=∠ADC
=90°
新知讲解
例题讲解
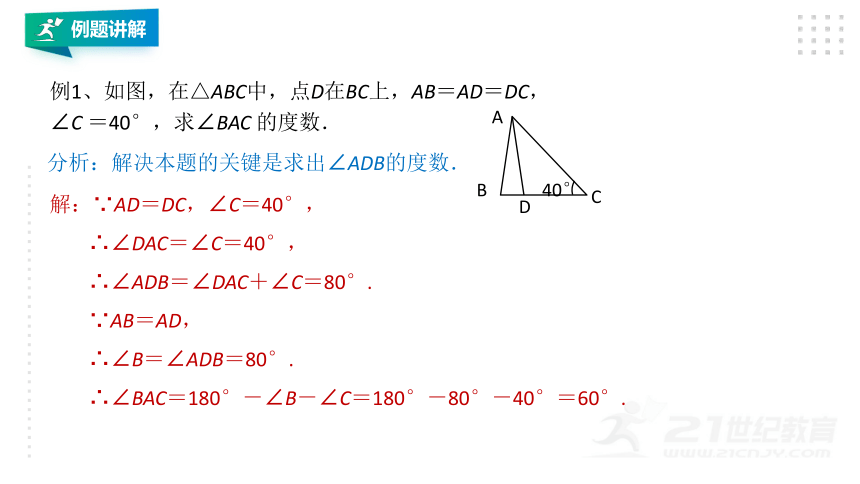
例1、如图,在△ABC中,点D在BC上,AB=AD=DC,
∠C
=40°,求∠BAC
的度数.
分析:解决本题的关键是求出∠ADB的度数.
解:∵AD=DC,∠C=40°,
∴∠DAC=∠C=40°,
∴∠ADB=∠DAC+∠C=80°.
∵AB=AD,
∴∠B=∠ADB=80°.
∴∠BAC=180°-∠B-∠C=180°-80°-40°=60°.
A
B
D
C
40°
当堂练习
已知:在△ABC中
,AB=AC,∠
B=80
°,求∠
C和∠
A的大小.
解:
A
B
C
课堂达标
请回答下列问题:
(1)
等腰三角形的一边长为3,一边长为5,那么它的周长是______
(2)等腰三角形的一边长为3,一边长为7,那么它的周长是______
(3)
等腰三角形的一边长为4,周长为9,那么它的腰长是________
(4)
等腰三角形的腰长是3,则底边长a的取值范围是______
(5)
等腰三角形的底边长是3,则腰长a的取值范围是______
11或13
17
04或2.5
a>1.5
知识讲解
因为等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到,∠B=
∠
C,
同理可得
∠A=∠B,
所以
∠A=∠B=∠C,
又由
∠A+∠B+∠C=180°,
从而推出
∠A=∠B=∠C=60°.
也就是说:等边三角形的各个角都相等,并且每一个角都等于60°.
三条边都相等的三角形是等边三角形,它也是轴对称图形,那么等边三角形的每个角的度数是多少呢?它有几条对称轴?
A
C
B
等边三角形的三条边都相等,三个角都相等,也称为正三角形.
三条对称轴
等边三角形的性质
知识讲解
等边三角形的性质:
等边三角形的各个内角都等于60°
例题讲解
例2、求等边三角形三个内角的度数.
解:由已知:AB=AC=BC,
∵AB=AC
(已知)
∴∠B=∠C
(等边对等角)
∴∠A=∠B=∠C
∵
∠A+∠B+∠C=180°
∴
∠A=
∠B=
∠C=60°
已知:
如图
,在△ABC中,AB=AC,BD,CE分别是
∠ABC
,∠ACB的平分线.求证:BD=CE
.
例3、求证“等腰三角形两底角的平分线相等”
A
E
D
C
B
例题讲解
分析:要证明BD=CE
,只需证明△BCE≌△CBD(或
ABD≌△ACE)因为
BC
是△BCE和
△CBD
的公共边,
所以只需证明∠
ABC=
∠
ACB,
∠BCE=
∠CBD.
这
可由已知AB=AC,BD和CE是△ABC的两条角平分线
得到
.
上述从所求出发的分析思路可以简明地表示成下图
BD=CE
△BCE≌△CBD
∠
ABC=
∠
ACB
∠BCE
=
∠CBD
BC=CB
AB=AC
BD,CE是△ABC的角平分线
例题讲解
A
E
D
C
B
证明:
如图
∵AB=AC
(已知),
∴∠ABC=
∠ACB
(等腰三角形的两个底角相等).
∵
BD,CE分别是∠
ABC,
∠ACB的平分线,
∴
∠CBD=
∠ABC,
∠BCE=
∠ACB
(角平分线的定义),
∴
∠CBD=∠BCE.
又∵BC=CB
(公共边),
∴
△BCE≌△CBD
(ASA).
∴
BD=CE.
(全等三角形的对应边相等).
例题讲解
课堂小结
1.
等腰三角形性质定理1:等腰三角形的两个底角相等.这个定理也可以说成在同一个三角形中,等边对等角.
2.
等边三角形的各个内角都等于60°.
课堂练习
1、如图,在△ABC中,AB=AC,DE∥BC,∠ADE=48°,
则下列结论中,错误的是
(
)
A.
∠B=48°
B.
∠AED=66°
C.
∠A=84°
D.
∠B+∠C=96°
解析:∵DE∥BC,∠ADE=48°,
∴∠B=∠ADE=48°.
∵AB=AC,∴∠C=∠B=48°,
∴∠B+∠C=96°,
∴∠A=180°-∠B-∠C=84°.
∵DE∥BC,∴∠AED=∠C=48°.
∴只有B错误.
B
A
D
E
C
B
课堂练习
(1)等腰三角形一个底角为75°,它的另外两个角为________
.
(2)等腰三角形一个角为70°,它的另外两个角为
__________
__________.
(3)等腰三角形一个角为110°,它的另外两个角为________.
75°,30°
70°,40°或
35°,35°
2、填空题
55°,55°
课堂练习
(4)如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则
∠1=
.
第(4)题
解析:∵△ABC为等腰三角形,
∠BAC=90°,
∴∠ABC=∠ACB=45°.
∵直线m∥n,
∴∠1=∠ABC=45°.
45°
A
m
C
B
1
n
课堂练习
A
B
C
D
3、如图,在△ABC中
,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数.
(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠C=∠BDC=∠ABC.
△ABC,
△ABD,
△BCD.
课堂练习
A
B
C
D
x
2x
2x
2x
(3)观察∠BDC与∠A、∠ABD的关系,∠ABC、∠C呢?
∠BDC=
∠A+∠ABD=2∠A=2∠ABD,
∠ABC=
∠BDC=2∠A,
∠C=∠BDC=2∠A
.
(4)设∠A=x,请把△
ABC的内角和用含x的式子表示出来.
∵
∠A+∠ABC+∠C=180
°,
∴x+2x+2x=180
°.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180
°
,
解得x=36
°
.
在△ABC中,∠A=36°,∠ABC=∠C=72°.
A
B
C
D
x
2x
2x
2x
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
2.3等腰三角形的性质定理
浙教版
八年级上
新知导入
将一把等腰三角尺和一个重锤如图1放置,就能检查一根讲台边沿是否水平,你知道为什么吗?
复习导入
有两条边相等的三角形叫做等腰三角形
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
探究归纳
剪一张等腰三角形的半透明纸片,每人所剪的等腰三角形的大小和形状可以不一样,如图,把纸片对折,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?
A
B
C
D
等腰三角形的性质
1.
等腰三角形是轴对称图形.
我们可以得出结论:
A
C
B
D
折痕AD所在直线是等腰三角形的对称轴.
你还有新的发现吗?
∠B、∠C
是等腰三角形的
.
底角
∠B
=∠C
所以我们可以描述为:
等腰三角形的两个底角相等.
2.
探究归纳
等腰三角形的性质定理1:
等腰三角形的两个底角相等
(简写成“在同一个三角形中,
等边对等角”).
新知讲解
已知:如图,△ABC
中,AB=AC,求证:∠B=∠C
.
证明:作顶角∠BAC的平分线AD.
在△ABD与△ACD中,
AB=AC
(已知),
∠BAD=∠CAD
(角平分线的定义),
AD=AD
(公共边),
∴
△ABD
≌
△ACD
(SAS),
∴
∠B=∠C
(全等三角形的对应角相等)
A
B
C
分析:由上述操作可以得到启发,即添加等腰三角形的顶角平分线AD,然后证明△ABD
≌
△ACD.
D
除了上述结论,你还能得出哪些结论?
新知讲解
想一想:
刚才的证明除了能得到∠B=∠C
,你还能发现什么?
重合的线段
重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B
=
∠C
∠BAD
=
∠CAD
∠ADB
=∠ADC
=90°
新知讲解
例题讲解
例1、如图,在△ABC中,点D在BC上,AB=AD=DC,
∠C
=40°,求∠BAC
的度数.
分析:解决本题的关键是求出∠ADB的度数.
解:∵AD=DC,∠C=40°,
∴∠DAC=∠C=40°,
∴∠ADB=∠DAC+∠C=80°.
∵AB=AD,
∴∠B=∠ADB=80°.
∴∠BAC=180°-∠B-∠C=180°-80°-40°=60°.
A
B
D
C
40°
当堂练习
已知:在△ABC中
,AB=AC,∠
B=80
°,求∠
C和∠
A的大小.
解:
A
B
C
课堂达标
请回答下列问题:
(1)
等腰三角形的一边长为3,一边长为5,那么它的周长是______
(2)等腰三角形的一边长为3,一边长为7,那么它的周长是______
(3)
等腰三角形的一边长为4,周长为9,那么它的腰长是________
(4)
等腰三角形的腰长是3,则底边长a的取值范围是______
(5)
等腰三角形的底边长是3,则腰长a的取值范围是______
11或13
17
0
a>1.5
知识讲解
因为等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到,∠B=
∠
C,
同理可得
∠A=∠B,
所以
∠A=∠B=∠C,
又由
∠A+∠B+∠C=180°,
从而推出
∠A=∠B=∠C=60°.
也就是说:等边三角形的各个角都相等,并且每一个角都等于60°.
三条边都相等的三角形是等边三角形,它也是轴对称图形,那么等边三角形的每个角的度数是多少呢?它有几条对称轴?
A
C
B
等边三角形的三条边都相等,三个角都相等,也称为正三角形.
三条对称轴
等边三角形的性质
知识讲解
等边三角形的性质:
等边三角形的各个内角都等于60°
例题讲解
例2、求等边三角形三个内角的度数.
解:由已知:AB=AC=BC,
∵AB=AC
(已知)
∴∠B=∠C
(等边对等角)
∴∠A=∠B=∠C
∵
∠A+∠B+∠C=180°
∴
∠A=
∠B=
∠C=60°
已知:
如图
,在△ABC中,AB=AC,BD,CE分别是
∠ABC
,∠ACB的平分线.求证:BD=CE
.
例3、求证“等腰三角形两底角的平分线相等”
A
E
D
C
B
例题讲解
分析:要证明BD=CE
,只需证明△BCE≌△CBD(或
ABD≌△ACE)因为
BC
是△BCE和
△CBD
的公共边,
所以只需证明∠
ABC=
∠
ACB,
∠BCE=
∠CBD.
这
可由已知AB=AC,BD和CE是△ABC的两条角平分线
得到
.
上述从所求出发的分析思路可以简明地表示成下图
BD=CE
△BCE≌△CBD
∠
ABC=
∠
ACB
∠BCE
=
∠CBD
BC=CB
AB=AC
BD,CE是△ABC的角平分线
例题讲解
A
E
D
C
B
证明:
如图
∵AB=AC
(已知),
∴∠ABC=
∠ACB
(等腰三角形的两个底角相等).
∵
BD,CE分别是∠
ABC,
∠ACB的平分线,
∴
∠CBD=
∠ABC,
∠BCE=
∠ACB
(角平分线的定义),
∴
∠CBD=∠BCE.
又∵BC=CB
(公共边),
∴
△BCE≌△CBD
(ASA).
∴
BD=CE.
(全等三角形的对应边相等).
例题讲解
课堂小结
1.
等腰三角形性质定理1:等腰三角形的两个底角相等.这个定理也可以说成在同一个三角形中,等边对等角.
2.
等边三角形的各个内角都等于60°.
课堂练习
1、如图,在△ABC中,AB=AC,DE∥BC,∠ADE=48°,
则下列结论中,错误的是
(
)
A.
∠B=48°
B.
∠AED=66°
C.
∠A=84°
D.
∠B+∠C=96°
解析:∵DE∥BC,∠ADE=48°,
∴∠B=∠ADE=48°.
∵AB=AC,∴∠C=∠B=48°,
∴∠B+∠C=96°,
∴∠A=180°-∠B-∠C=84°.
∵DE∥BC,∴∠AED=∠C=48°.
∴只有B错误.
B
A
D
E
C
B
课堂练习
(1)等腰三角形一个底角为75°,它的另外两个角为________
.
(2)等腰三角形一个角为70°,它的另外两个角为
__________
__________.
(3)等腰三角形一个角为110°,它的另外两个角为________.
75°,30°
70°,40°或
35°,35°
2、填空题
55°,55°
课堂练习
(4)如图,直线m∥n,△ABC为等腰三角形,∠BAC=90°,则
∠1=
.
第(4)题
解析:∵△ABC为等腰三角形,
∠BAC=90°,
∴∠ABC=∠ACB=45°.
∵直线m∥n,
∴∠1=∠ABC=45°.
45°
A
m
C
B
1
n
课堂练习
A
B
C
D
3、如图,在△ABC中
,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数.
(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠C=∠BDC=∠ABC.
△ABC,
△ABD,
△BCD.
课堂练习
A
B
C
D
x
2x
2x
2x
(3)观察∠BDC与∠A、∠ABD的关系,∠ABC、∠C呢?
∠BDC=
∠A+∠ABD=2∠A=2∠ABD,
∠ABC=
∠BDC=2∠A,
∠C=∠BDC=2∠A
.
(4)设∠A=x,请把△
ABC的内角和用含x的式子表示出来.
∵
∠A+∠ABC+∠C=180
°,
∴x+2x+2x=180
°.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
于是在△ABC中,有
∠A+∠ABC+∠C=x+2x+2x=180
°
,
解得x=36
°
.
在△ABC中,∠A=36°,∠ABC=∠C=72°.
A
B
C
D
x
2x
2x
2x
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
