浙教版数学七年级上册 阅读材料 数学中的符号(教案)
文档属性
| 名称 | 浙教版数学七年级上册 阅读材料 数学中的符号(教案) | 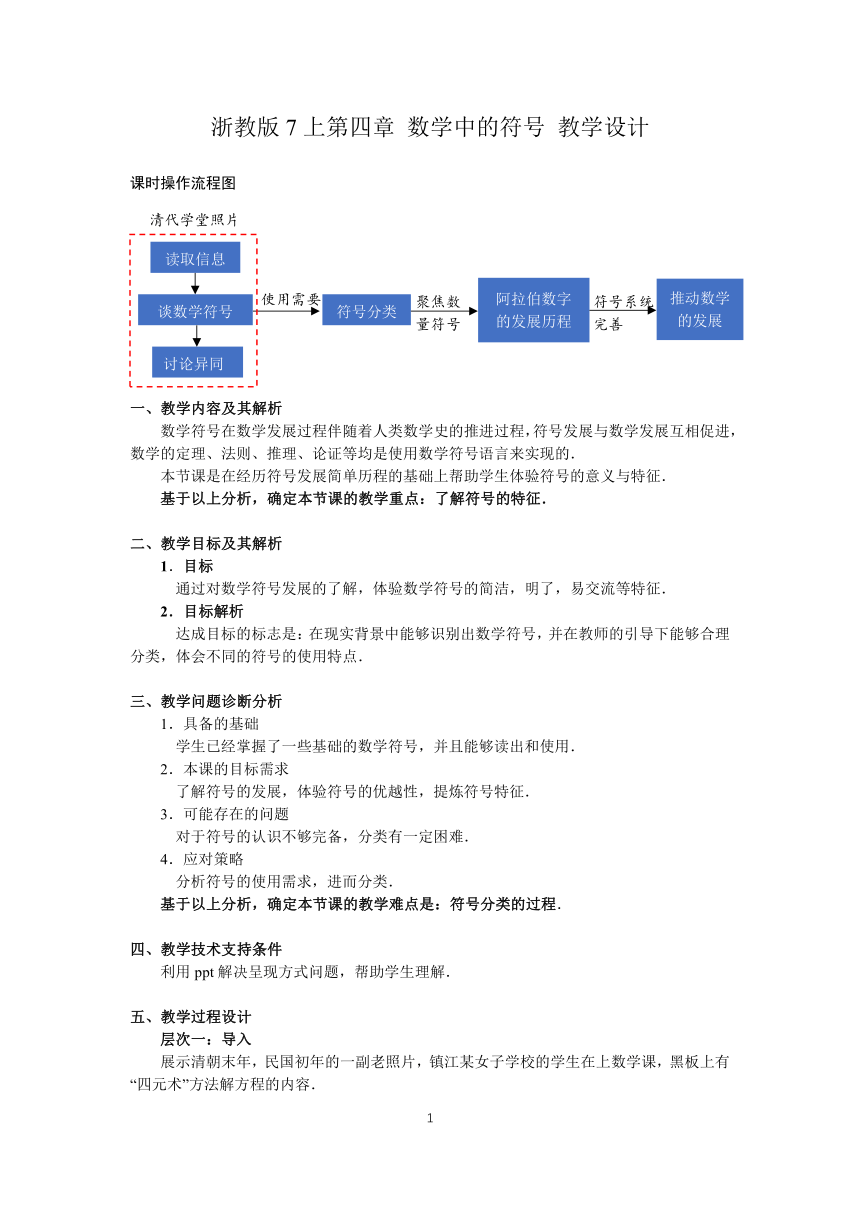 | |
| 格式 | docx | ||
| 文件大小 | 420.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 20:45:39 | ||
图片预览



文档简介
浙教版7上第四章
数学中的符号
教学设计
课时操作流程图
一、教学内容及其解析
数学符号在数学发展过程伴随着人类数学史的推进过程,符号发展与数学发展互相促进,数学的定理、法则、推理、论证等均是使用数学符号语言来实现的.
本节课是在经历符号发展简单历程的基础上帮助学生体验符号的意义与特征.
基于以上分析,确定本节课的教学重点:了解符号的特征.
二、教学目标及其解析
1.目标
通过对数学符号发展的了解,体验数学符号的简洁,明了,易交流等特征.
2.目标解析
达成目标的标志是:在现实背景中能够识别出数学符号,并在教师的引导下能够合理分类,体会不同的符号的使用特点.
三、教学问题诊断分析
1.具备的基础
学生已经掌握了一些基础的数学符号,并且能够读出和使用.
2.本课的目标需求
了解符号的发展,体验符号的优越性,提炼符号特征.
3.可能存在的问题
对于符号的认识不够完备,分类有一定困难.
4.应对策略
分析符号的使用需求,进而分类.
基于以上分析,确定本节课的教学难点是:符号分类的过程.
四、教学技术支持条件
利用ppt解决呈现方式问题,帮助学生理解.
五、教学过程设计
层次一:导入
展示清朝末年,民国初年的一副老照片,镇江某女子学校的学生在上数学课,黑板上有“四元术”方法解方程的内容.
【问题1】你从照片中能读出什么信息?
6人小组合作讨论.
学生谈发现的信息,大致可能为:上数学课、解方程、“天,地”相当于“x,y”,加减乘除等运算符号等等.
板书
现代方程
【设计意图】让学生体会,在清朝末年,人们已经基本能够运用与现代方程体系差异不大的方法解方程,基于符号体系的建立才能解决运算问题,这说明,符号体系已经在中国得到使用.
【追问】谈到符号,黑板呈现的符号与现行的符号有没有差异?
有差异,差异主要在于符号更简洁,方便。
【设计意图】帮助学生体验:
1.基本的运算符号已经在使用,加减乘除等等。
2.都是在用符号表示未知量。
3.数学内部的知识没有发生改变,只是符号的使用使问题的表达更简洁更通用。
层次二:符号的分类
【问题2】面对这么多的符号,需要加以分类.
6人小组合作讨论.
(1)数量符号:如10,,π,a,x等;
(2)运算符号:+、-、×、÷、√
等;
(3)关系符号:=、≠、≈等;
(4)结合符号:()、{
}等;
(5)性质符号:±、||等;
(6)省略符号:△等;
……
【设计意图】
1.体验不同符号的使用意义,比如数量符号用来记数;运算符号用于运算;关系符号用来比较数量之间的关系;结合符号用于改变运算顺序;性质符号用来表示特征;省略符号使用书写或者表达更方便简洁……;
2.符号使数学体系易于学习,明了;
3.符号要能够通用,交流便捷.
层次三:数量符号中的阿拉伯数字符号形态演变
(一)阿拉伯数字是最通用的计数符号,它的发展历程:
【问题3】思考,大家从小学开始就一直在接触的这些数,为什么这几个简单的数字能够通用?阿拉伯数字究竟特殊在哪里?
6人小组合作讨论.
【设计意图】由于这一套符号的特有的规则,使得阿拉伯数字得以通用.帮助学生回顾体会阿拉伯数字符号的优越之处:
1.只有0~9十个基本符号.
2.十进制,逢十进一.
3.位置记数制,从右到左,个位、十位、百位、千位、万位……,逐位上升.
(二)0~9的发展历程
1.古埃及的象形数字(公元前3400年左右)
结论:直观,很先进,但是限于数字累计.
2.巴比伦楔形数字(公元前2400年左右)
结论:已经有数位的萌芽状态了.但还是基于数,巴比伦的楔形数字是60进制的.
3.中国甲骨文数字(公元前1600年左右)
结论:已经有了用符号表示数的痕迹,但是还是比较复杂.
4.希腊阿提卡数字(公元前500年左右)
结论:已经有了数位的痕迹,很有意义,还是复杂.
5.中国筹算数码(公元前500年左右)
结论:以5为单位的表示方法,数位非常清晰了,就是九个符号在组合,不同位置表达的意义已经不同了.
6.印度数字符号(公元5世纪)
结论:数量符号的发展经过了2900年还没有看到0,直到古印度0才出现,形成完整的10个记数符号,计数系统完整了.
【设计意图】
经历记数符号的发展过程,帮助学生体会数字符号系统产生背后的人类智慧.
层次四:基于符号系统的数学发展
人们通过用数学符号组成的语言交流数学思想,认识世界的奥秘,并把数学成果应用于
各种人类实际问题。数学的定理、法则、推理、论证等均是使用数学符号语言来实现的。
【问题4】符号系统的完善,才带来数学运算的发展,才能研究数量之间的关系.古代
原题呈现1:
九章算术—卷第一—方田—【七】
今有三分之一,五分之二。问合之得几何?
答曰:十五分之十一
译文:
现有,,问相加得多少?
答:
【设计意图】体验符号的基础地位,以及运算的简洁.
古代原题呈现2:
“九算术”中著名问题之一
九章算术----卷第八---方程---【一】
今有上禾三秉,中禾二秉,下禾一秉,实三十九斗;
上禾二秉,中禾三秉,下禾一秉,实三十四斗;
上禾一秉,中禾二秉,下禾三秉,实二十六斗。
问上、中、下禾实一秉各几何?
译文:
今有上禾3束,中禾2束,下禾1束,实39斗;
上禾2束,中禾3束,下禾1束,实34斗;
上禾1束,中禾2束,下禾3束,实26斗。
问上、中、下禾实每一束得实各多少?
算筹表示:
【设计意图】
1.体验符号系统的完善带来的运算的简便.
2.中国古代数学成就欣赏:古代中国的“九章算术”创立了机械化算法体系,是中国数学体系确立的核心标志,代表了东方数学的最高成就。
3.这个问题相当于现代的“矩阵”,解线性方程时使用的直除法,与现在的矩阵初等变换一致,是世界上最早的线性方程。
小结
1.数学符号具有简洁、明了、易交流的特征.
2.数学符号化促使了代数学的产生,代数计算变得精确和方便,也使计算方法系统化.促进了数学逻辑的发展.
2
数学中的符号
教学设计
课时操作流程图
一、教学内容及其解析
数学符号在数学发展过程伴随着人类数学史的推进过程,符号发展与数学发展互相促进,数学的定理、法则、推理、论证等均是使用数学符号语言来实现的.
本节课是在经历符号发展简单历程的基础上帮助学生体验符号的意义与特征.
基于以上分析,确定本节课的教学重点:了解符号的特征.
二、教学目标及其解析
1.目标
通过对数学符号发展的了解,体验数学符号的简洁,明了,易交流等特征.
2.目标解析
达成目标的标志是:在现实背景中能够识别出数学符号,并在教师的引导下能够合理分类,体会不同的符号的使用特点.
三、教学问题诊断分析
1.具备的基础
学生已经掌握了一些基础的数学符号,并且能够读出和使用.
2.本课的目标需求
了解符号的发展,体验符号的优越性,提炼符号特征.
3.可能存在的问题
对于符号的认识不够完备,分类有一定困难.
4.应对策略
分析符号的使用需求,进而分类.
基于以上分析,确定本节课的教学难点是:符号分类的过程.
四、教学技术支持条件
利用ppt解决呈现方式问题,帮助学生理解.
五、教学过程设计
层次一:导入
展示清朝末年,民国初年的一副老照片,镇江某女子学校的学生在上数学课,黑板上有“四元术”方法解方程的内容.
【问题1】你从照片中能读出什么信息?
6人小组合作讨论.
学生谈发现的信息,大致可能为:上数学课、解方程、“天,地”相当于“x,y”,加减乘除等运算符号等等.
板书
现代方程
【设计意图】让学生体会,在清朝末年,人们已经基本能够运用与现代方程体系差异不大的方法解方程,基于符号体系的建立才能解决运算问题,这说明,符号体系已经在中国得到使用.
【追问】谈到符号,黑板呈现的符号与现行的符号有没有差异?
有差异,差异主要在于符号更简洁,方便。
【设计意图】帮助学生体验:
1.基本的运算符号已经在使用,加减乘除等等。
2.都是在用符号表示未知量。
3.数学内部的知识没有发生改变,只是符号的使用使问题的表达更简洁更通用。
层次二:符号的分类
【问题2】面对这么多的符号,需要加以分类.
6人小组合作讨论.
(1)数量符号:如10,,π,a,x等;
(2)运算符号:+、-、×、÷、√
等;
(3)关系符号:=、≠、≈等;
(4)结合符号:()、{
}等;
(5)性质符号:±、||等;
(6)省略符号:△等;
……
【设计意图】
1.体验不同符号的使用意义,比如数量符号用来记数;运算符号用于运算;关系符号用来比较数量之间的关系;结合符号用于改变运算顺序;性质符号用来表示特征;省略符号使用书写或者表达更方便简洁……;
2.符号使数学体系易于学习,明了;
3.符号要能够通用,交流便捷.
层次三:数量符号中的阿拉伯数字符号形态演变
(一)阿拉伯数字是最通用的计数符号,它的发展历程:
【问题3】思考,大家从小学开始就一直在接触的这些数,为什么这几个简单的数字能够通用?阿拉伯数字究竟特殊在哪里?
6人小组合作讨论.
【设计意图】由于这一套符号的特有的规则,使得阿拉伯数字得以通用.帮助学生回顾体会阿拉伯数字符号的优越之处:
1.只有0~9十个基本符号.
2.十进制,逢十进一.
3.位置记数制,从右到左,个位、十位、百位、千位、万位……,逐位上升.
(二)0~9的发展历程
1.古埃及的象形数字(公元前3400年左右)
结论:直观,很先进,但是限于数字累计.
2.巴比伦楔形数字(公元前2400年左右)
结论:已经有数位的萌芽状态了.但还是基于数,巴比伦的楔形数字是60进制的.
3.中国甲骨文数字(公元前1600年左右)
结论:已经有了用符号表示数的痕迹,但是还是比较复杂.
4.希腊阿提卡数字(公元前500年左右)
结论:已经有了数位的痕迹,很有意义,还是复杂.
5.中国筹算数码(公元前500年左右)
结论:以5为单位的表示方法,数位非常清晰了,就是九个符号在组合,不同位置表达的意义已经不同了.
6.印度数字符号(公元5世纪)
结论:数量符号的发展经过了2900年还没有看到0,直到古印度0才出现,形成完整的10个记数符号,计数系统完整了.
【设计意图】
经历记数符号的发展过程,帮助学生体会数字符号系统产生背后的人类智慧.
层次四:基于符号系统的数学发展
人们通过用数学符号组成的语言交流数学思想,认识世界的奥秘,并把数学成果应用于
各种人类实际问题。数学的定理、法则、推理、论证等均是使用数学符号语言来实现的。
【问题4】符号系统的完善,才带来数学运算的发展,才能研究数量之间的关系.古代
原题呈现1:
九章算术—卷第一—方田—【七】
今有三分之一,五分之二。问合之得几何?
答曰:十五分之十一
译文:
现有,,问相加得多少?
答:
【设计意图】体验符号的基础地位,以及运算的简洁.
古代原题呈现2:
“九算术”中著名问题之一
九章算术----卷第八---方程---【一】
今有上禾三秉,中禾二秉,下禾一秉,实三十九斗;
上禾二秉,中禾三秉,下禾一秉,实三十四斗;
上禾一秉,中禾二秉,下禾三秉,实二十六斗。
问上、中、下禾实一秉各几何?
译文:
今有上禾3束,中禾2束,下禾1束,实39斗;
上禾2束,中禾3束,下禾1束,实34斗;
上禾1束,中禾2束,下禾3束,实26斗。
问上、中、下禾实每一束得实各多少?
算筹表示:
【设计意图】
1.体验符号系统的完善带来的运算的简便.
2.中国古代数学成就欣赏:古代中国的“九章算术”创立了机械化算法体系,是中国数学体系确立的核心标志,代表了东方数学的最高成就。
3.这个问题相当于现代的“矩阵”,解线性方程时使用的直除法,与现在的矩阵初等变换一致,是世界上最早的线性方程。
小结
1.数学符号具有简洁、明了、易交流的特征.
2.数学符号化促使了代数学的产生,代数计算变得精确和方便,也使计算方法系统化.促进了数学逻辑的发展.
2
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
