浙教版数学七年级上册 4.2代数式(共19张)
文档属性
| 名称 | 浙教版数学七年级上册 4.2代数式(共19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-28 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
代数式
课前复习:
任意实数
数在具体情景有具体意义
数量关系的变化规律
字母可以表示
.
字母的取值范围受
的限制.
字母能表示
.
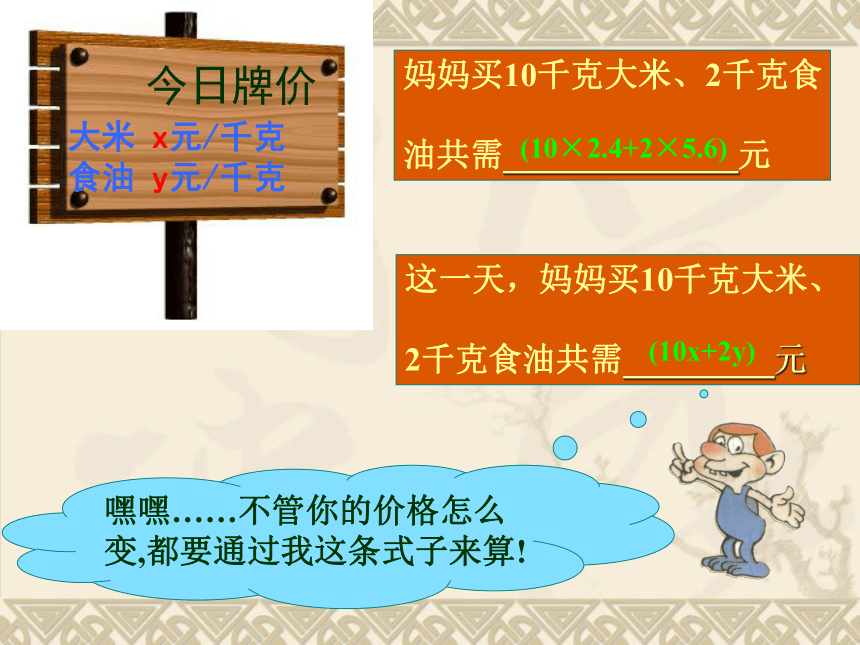
妈妈买10千克大米、2千克食
油共需______________元
今日牌价
大米
2.4元/千克
食油
5.6元/千克
今日牌价
大米
x元/千克
食油
y元/千克
这一天,妈妈买10千克大米、
2千克食油共需_________元
嘿嘿……不管你的价格怎么变,都要通过我这条式子来算!
(10x+2y)
(10×2.4+2×5.6)
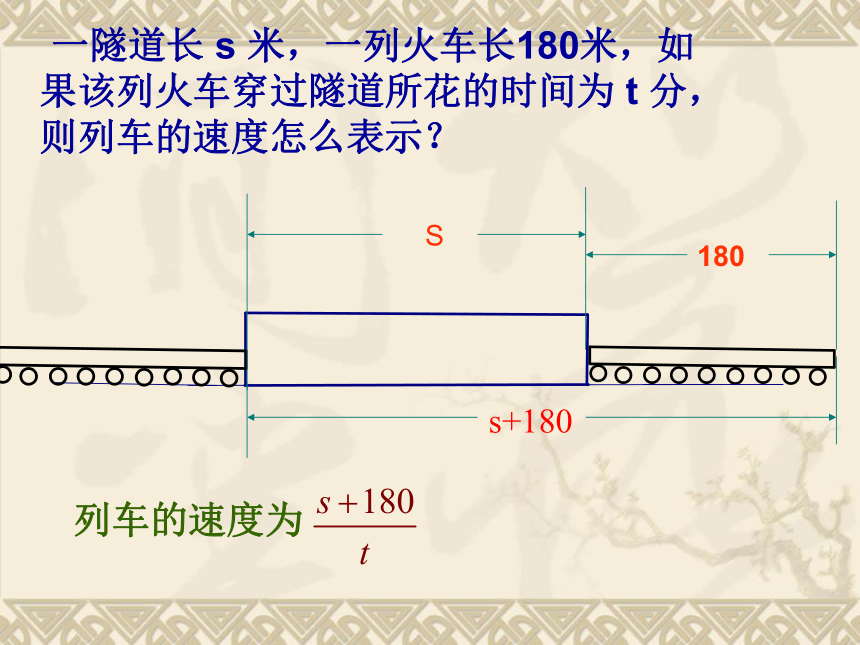
1.一隧道长
s
米,一列火车长180米,如果该列火车穿过隧道所花的时间为
t
分,则列车的速度怎么表示?
问题1
什么火车叫做穿过隧道?
从车头进洞开始到车尾离洞结束。
问题2
火车穿过隧道需经过多少路程?
你能得出表示列车
速度的算式吗?
S
180
一隧道长
s
米,一列火车长180米,如果该列火车穿过隧道所花的时间为
t
分,则列车的速度怎么表示?
列车的速度为
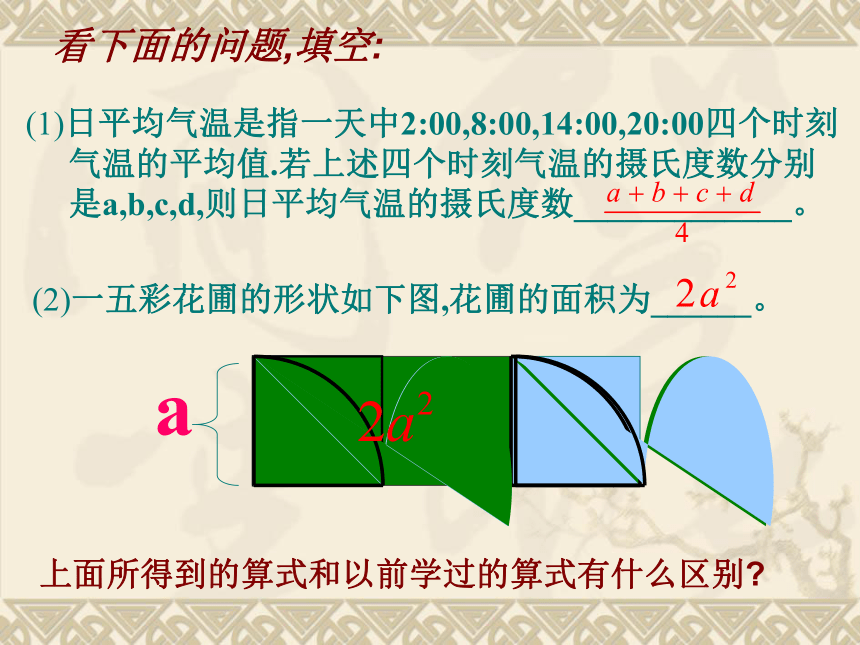
(1)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻气温的平均值.若上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数_____________。
(2)一五彩花圃的形状如下图,花圃的面积为______。
a
上面所得到的算式和以前学过的算式有什么区别?
看下面的问题,填空:
像
,这样含有字母的数学表达式称为代数式.
一个代数式由数、表示数的字母和运算符号组成.单独一个数或者一个字母也称代数式.
这里的运算符号是指加、减、乘、除、乘方和开方。
(2)
1÷a
通常写作
;
代数式的组成:
①
一个代数式由数,表示数的字母和运算符号组成;
②
单独一个数或者一个字母也称为代数式.
式子不含“=”、“>”、“<”、“≤”、“≥”。
(3)
数字通常写在字母前面;
(1)
a×b
通常写作
a·b
或
ab
;
(4)带分数一般写成假分数.
如:
×a
通常写作
代数式的规范写法:
做一做
在x,1,x
-
2,s=ab,
,v=sh中
代数式的个数是( )个
A. 5 B.
4 C.
3 D.
2
2
B
辨一辨
下列各式是代数式吗?
(1)2x+3y
(2)3xy-5
(3)5x=4y-2
(4)
m
(5)
-7
(6)
x﹥y
(7)
(8)
用语言叙述下列代数式的意义:
(1)苹果每千克的价格是x元,则
可以怎样解释?
(2)8a3可以怎样解释?
(3)10x+5y可以怎样解释?
例1.用代数式表示:
(1)x的3倍与3的差;
(2)x的2倍与y的
的和;
(3)a与b的和的平方;
(4)2a的立方根。
课内练习
(1)a与b的
的和;
(2)a与b的平方的差;
(3)m与n的差的平方;
(4)v1,v2的和除s所得的商;
(5)x与1的差的平方根。
例2
一辆汽车以80千米/时的速度行驶,从A城到B城需
t
时。如果该车的行驶速度增加
v千米/时,那么从A城到B城需要多少时间?
80千米/时
t小时
A
B
(80+
v
)千米/时
?小时
解:
由题意得,
A
、B两城之间的距离为80t千米.
如果该车的行驶速度增加v千米/时,
那么汽车的行驶速度为(80+v)千米/时,
此时从A城到B城需要
时.
答:
当汽车的行驶速度增加v千米/时,从A城到
B城需要
时.
用文字叙述下列代数式的意义;
(1)
2a-3
(2)
(3)
思维拓展
2)甲种日记本每本x元,乙种日记本每本y元,
用代数式表示购买10本甲种日记本和5本乙
种日记本的总钱数是多少?
3)甲乙两人加工同一种产品,甲每天加工x
只产品,乙每天加工y只产品,甲加工了
10天,乙加工了5天,试用代数式表示加
工产品的总数?
1)已知甲数比乙数的2倍少1.设乙数为X,用关于X
的代数式表示甲数
一个旅游团有成人x人,学生y人,那么
该旅游团应付多少门票费?
若该旅游团有成人37人,学生15人,那么
该旅游团应付多少门票费?
售票处
成
人
票
价
10
元
学
生
票
价
5
元
如图:这棵树的高度是1.2米,在某时刻测得它影子
的长度是2米,此时这棵树的高度是它影子的多少倍?
如果用L表示物体影子的长度,如何用代数式表
示此时此地物体的高度?
该地某建筑物的影长为5.5米,那么此时它的高
度是多少?
课堂小结:
本课时学习了列代数式,列代数式要注意的是:
要正确写出代数式要注意
(1)审清题,弄懂一些术语
(2)抓住关键词,弄清运算顺序
(3)一般先读的先写
同时一个代数式可表示不同的意义。
在代数式中同一意义的量应用同一个字母表示,不同意义的量应用不同的字母表示。
(4)用代数式表示应用问题时,还弄清题中的数量关系。
代数式
课前复习:
任意实数
数在具体情景有具体意义
数量关系的变化规律
字母可以表示
.
字母的取值范围受
的限制.
字母能表示
.
妈妈买10千克大米、2千克食
油共需______________元
今日牌价
大米
2.4元/千克
食油
5.6元/千克
今日牌价
大米
x元/千克
食油
y元/千克
这一天,妈妈买10千克大米、
2千克食油共需_________元
嘿嘿……不管你的价格怎么变,都要通过我这条式子来算!
(10x+2y)
(10×2.4+2×5.6)
1.一隧道长
s
米,一列火车长180米,如果该列火车穿过隧道所花的时间为
t
分,则列车的速度怎么表示?
问题1
什么火车叫做穿过隧道?
从车头进洞开始到车尾离洞结束。
问题2
火车穿过隧道需经过多少路程?
你能得出表示列车
速度的算式吗?
S
180
一隧道长
s
米,一列火车长180米,如果该列火车穿过隧道所花的时间为
t
分,则列车的速度怎么表示?
列车的速度为
(1)日平均气温是指一天中2:00,8:00,14:00,20:00四个时刻气温的平均值.若上述四个时刻气温的摄氏度数分别是a,b,c,d,则日平均气温的摄氏度数_____________。
(2)一五彩花圃的形状如下图,花圃的面积为______。
a
上面所得到的算式和以前学过的算式有什么区别?
看下面的问题,填空:
像
,这样含有字母的数学表达式称为代数式.
一个代数式由数、表示数的字母和运算符号组成.单独一个数或者一个字母也称代数式.
这里的运算符号是指加、减、乘、除、乘方和开方。
(2)
1÷a
通常写作
;
代数式的组成:
①
一个代数式由数,表示数的字母和运算符号组成;
②
单独一个数或者一个字母也称为代数式.
式子不含“=”、“>”、“<”、“≤”、“≥”。
(3)
数字通常写在字母前面;
(1)
a×b
通常写作
a·b
或
ab
;
(4)带分数一般写成假分数.
如:
×a
通常写作
代数式的规范写法:
做一做
在x,1,x
-
2,s=ab,
,v=sh中
代数式的个数是( )个
A. 5 B.
4 C.
3 D.
2
2
B
辨一辨
下列各式是代数式吗?
(1)2x+3y
(2)3xy-5
(3)5x=4y-2
(4)
m
(5)
-7
(6)
x﹥y
(7)
(8)
用语言叙述下列代数式的意义:
(1)苹果每千克的价格是x元,则
可以怎样解释?
(2)8a3可以怎样解释?
(3)10x+5y可以怎样解释?
例1.用代数式表示:
(1)x的3倍与3的差;
(2)x的2倍与y的
的和;
(3)a与b的和的平方;
(4)2a的立方根。
课内练习
(1)a与b的
的和;
(2)a与b的平方的差;
(3)m与n的差的平方;
(4)v1,v2的和除s所得的商;
(5)x与1的差的平方根。
例2
一辆汽车以80千米/时的速度行驶,从A城到B城需
t
时。如果该车的行驶速度增加
v千米/时,那么从A城到B城需要多少时间?
80千米/时
t小时
A
B
(80+
v
)千米/时
?小时
解:
由题意得,
A
、B两城之间的距离为80t千米.
如果该车的行驶速度增加v千米/时,
那么汽车的行驶速度为(80+v)千米/时,
此时从A城到B城需要
时.
答:
当汽车的行驶速度增加v千米/时,从A城到
B城需要
时.
用文字叙述下列代数式的意义;
(1)
2a-3
(2)
(3)
思维拓展
2)甲种日记本每本x元,乙种日记本每本y元,
用代数式表示购买10本甲种日记本和5本乙
种日记本的总钱数是多少?
3)甲乙两人加工同一种产品,甲每天加工x
只产品,乙每天加工y只产品,甲加工了
10天,乙加工了5天,试用代数式表示加
工产品的总数?
1)已知甲数比乙数的2倍少1.设乙数为X,用关于X
的代数式表示甲数
一个旅游团有成人x人,学生y人,那么
该旅游团应付多少门票费?
若该旅游团有成人37人,学生15人,那么
该旅游团应付多少门票费?
售票处
成
人
票
价
10
元
学
生
票
价
5
元
如图:这棵树的高度是1.2米,在某时刻测得它影子
的长度是2米,此时这棵树的高度是它影子的多少倍?
如果用L表示物体影子的长度,如何用代数式表
示此时此地物体的高度?
该地某建筑物的影长为5.5米,那么此时它的高
度是多少?
课堂小结:
本课时学习了列代数式,列代数式要注意的是:
要正确写出代数式要注意
(1)审清题,弄懂一些术语
(2)抓住关键词,弄清运算顺序
(3)一般先读的先写
同时一个代数式可表示不同的意义。
在代数式中同一意义的量应用同一个字母表示,不同意义的量应用不同的字母表示。
(4)用代数式表示应用问题时,还弄清题中的数量关系。
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
