浙教版数学七年级上册 4.6 整式的加减课件(1)(16张)
文档属性
| 名称 | 浙教版数学七年级上册 4.6 整式的加减课件(1)(16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 534.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-29 17:34:27 | ||
图片预览






文档简介
(共16张PPT)
同类项:
1、写出
2a2b
的一个同类项:
2、已知4a2b3与a2mbn-1是同类项,
则m=
____,n=_____.
合并同类项:
4
1
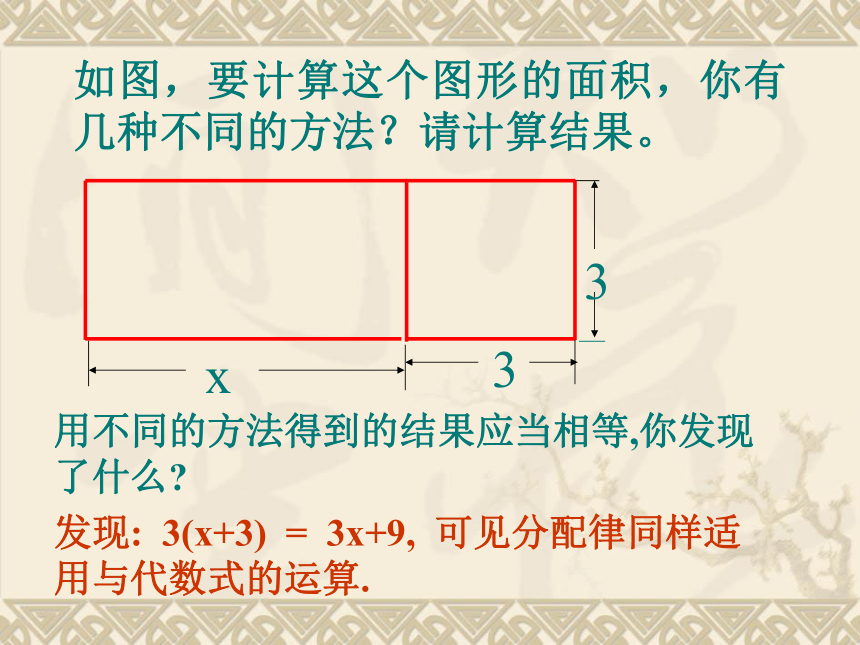
如图,要计算这个图形的面积,你有几种不同的方法?请计算结果。
3
3
x
用不同的方法得到的结果应当相等,你发现了什么?
发现:
3(x+3)
=
3x+9,
可见分配律同样适用与代数式的运算.
根据分配律,得
+(a-b+c)
-(a-b+c)
=
1×(a-b+c)
=
a-b+c
=
(-1)×(a-b+c)
=
-a+b-c
去括号法则:
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号;
辩一辩:指出下列各式是否正确?如果错误,请指出原因并改正.
a-(b-c+d)
=
a-b+c+d
-(a-b)+(-c+d)
=
a+b-c-d
a-3(b-2c)
=
a-3b+2c
(4)
x-2(-y-3z+1)
=
x-2y+6z
(1)去括号时应将括号前面的符号连同括号一起去掉.
(2)要注意括号前面是
“-”号时,去掉括号后,
括号里各项都要改变符号;不能只改变某几项而忘记改变其余的符号
(3)若括号前面是数字因数时,应乘以括号里的每一项,不要漏乘.
1、去括号:
(1)2(1-3x)
=
____
(2)-(
)
=
_
_
(3)-3
(
)
=
__
__
2、
= -( )
3、化简:
2n-(2-n)+(6n-2)
解:原式=2n-2+n+6n-2
=9n-4
=2n+n+6n-2-2
例1、化简并求值:
1、要掌握好此题的书写格式
2、整式的化简归结为去括号和
合并同类项
其中
1、化简:
(1)
(2)
(3)
2、化简并求值:
其中
3、下列式子正确的是(
)
A、x-(y-z)=x-y-z
B、-(x-y+z)=-x-y+z
C、x+2y-2z=x-2(y+z)
D、-a+c+d-b=
-
(a+b)+(c+d)
D
一种长方形餐桌的四周可坐6人用餐,现把n张这样的餐桌按如图方式拼接起来,问四周可坐多少人用餐?若用餐的人数有18人,则这样的餐桌需要多少张?
一种长方形餐桌的四周可坐6人用餐,现把n张这样的餐桌按如图方式拼接起来,问四周可坐多少人用餐?若用餐的人数有18人,则这样的餐桌需要多少张?
将一张长方形的纸对折,可得一条折痕。继续对折,使每次的折痕与上次的折痕平行,连续对折4次后,可得几条折痕?对折n次呢?
折叠
次数
1
2
3
4
5
n
折痕数
1
31
15
3
7
2n-1
探索规律:
探索规律:
如图:工地上有一堆圆形钢管,第一层有2根,第二层3根,第三层4根,……
你能说出第八层有几根吗?
第n层呢?
现有一列数:
2,4,8,16,
,64,
128,…
横线上是什么数?第n个数怎么表示?
……
同类项:
1、写出
2a2b
的一个同类项:
2、已知4a2b3与a2mbn-1是同类项,
则m=
____,n=_____.
合并同类项:
4
1
如图,要计算这个图形的面积,你有几种不同的方法?请计算结果。
3
3
x
用不同的方法得到的结果应当相等,你发现了什么?
发现:
3(x+3)
=
3x+9,
可见分配律同样适用与代数式的运算.
根据分配律,得
+(a-b+c)
-(a-b+c)
=
1×(a-b+c)
=
a-b+c
=
(-1)×(a-b+c)
=
-a+b-c
去括号法则:
括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变号;括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号;
辩一辩:指出下列各式是否正确?如果错误,请指出原因并改正.
a-(b-c+d)
=
a-b+c+d
-(a-b)+(-c+d)
=
a+b-c-d
a-3(b-2c)
=
a-3b+2c
(4)
x-2(-y-3z+1)
=
x-2y+6z
(1)去括号时应将括号前面的符号连同括号一起去掉.
(2)要注意括号前面是
“-”号时,去掉括号后,
括号里各项都要改变符号;不能只改变某几项而忘记改变其余的符号
(3)若括号前面是数字因数时,应乘以括号里的每一项,不要漏乘.
1、去括号:
(1)2(1-3x)
=
____
(2)-(
)
=
_
_
(3)-3
(
)
=
__
__
2、
= -( )
3、化简:
2n-(2-n)+(6n-2)
解:原式=2n-2+n+6n-2
=9n-4
=2n+n+6n-2-2
例1、化简并求值:
1、要掌握好此题的书写格式
2、整式的化简归结为去括号和
合并同类项
其中
1、化简:
(1)
(2)
(3)
2、化简并求值:
其中
3、下列式子正确的是(
)
A、x-(y-z)=x-y-z
B、-(x-y+z)=-x-y+z
C、x+2y-2z=x-2(y+z)
D、-a+c+d-b=
-
(a+b)+(c+d)
D
一种长方形餐桌的四周可坐6人用餐,现把n张这样的餐桌按如图方式拼接起来,问四周可坐多少人用餐?若用餐的人数有18人,则这样的餐桌需要多少张?
一种长方形餐桌的四周可坐6人用餐,现把n张这样的餐桌按如图方式拼接起来,问四周可坐多少人用餐?若用餐的人数有18人,则这样的餐桌需要多少张?
将一张长方形的纸对折,可得一条折痕。继续对折,使每次的折痕与上次的折痕平行,连续对折4次后,可得几条折痕?对折n次呢?
折叠
次数
1
2
3
4
5
n
折痕数
1
31
15
3
7
2n-1
探索规律:
探索规律:
如图:工地上有一堆圆形钢管,第一层有2根,第二层3根,第三层4根,……
你能说出第八层有几根吗?
第n层呢?
现有一列数:
2,4,8,16,
,64,
128,…
横线上是什么数?第n个数怎么表示?
……
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
