1.4二次函数的应用 分类提升训练 2021-2022学年浙教版九年级数学上册(word版含答案)
文档属性
| 名称 | 1.4二次函数的应用 分类提升训练 2021-2022学年浙教版九年级数学上册(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 367.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 08:46:57 | ||
图片预览




文档简介
2021-2022学年浙教版九年级数学上册《1.4二次函数的应用》分类提升训练(附答案)
一.抛物线与x轴的交点
1.抛物线y=(k﹣1)x2﹣x+1与x轴有交点,则k的取值范围是
.
2.已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是
.
3.如图,抛物线y=x2+5x+4与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接AC,点P在线段AC上,过点P作x轴的垂线交抛物线于点Q,则线段PQ长的最大值为
.
4.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣4x﹣12,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为
.
二.图象法求一元二次方程的近似根
5.二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx﹣t=0(b、t为实数)在﹣1<x<4的范围内有解,则t的取值范围是
.
三.二次函数与不等式(组)
6.如图,在平面直角坐标系中,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(2,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是( )
A.x<﹣1
B.x>2
C.﹣1<x<2
D.x<﹣1或x>2
四.根据实际问题列二次函数关系式
7.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825
B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900
D.y=﹣2(x﹣65)2+2000
8.在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,若a+b=5,则Rt△ABC的面积S关于边长c的函数关系式为( )
A.S=
B.S=
C.S=
D.S=
9.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门,已知计划中的建筑材料可建围墙(不包括门)的总长度为50m.设饲养室长为xm,占地面积为ym2,则y关于x的函数表达式是( )
A.y=﹣x2+50x
B.y=﹣x2+24x
C.y=﹣x2+25x
D.y=﹣x2+26x
10.矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点于点C重合,则该抛物线的函数表达式变为( )
A.y=x2﹣8x+14
B.y=x2+8x+14
C.y=x2+4x+3
D.y=x2﹣4x+3
11.某工厂今年一月份生产防疫护目镜的产量是20万件,计划之后两个月增加产量,如果月平均增长率为x,那么第一季度防疫护目镜的产量y(万件)与x之间的关系应表示为
.
12.某体育用品商店购进一批滑板,每块滑板利润为30元,一星期可卖出80块.商家决定降价促销,根据市场调查,每降价1元,则一星期可多卖出4块.设每块滑板降价x元,商店一星期销售这种滑板的利润是y元,则y与x之间的函数表达式为
.
13.如图,有一座拱桥洞呈抛物线形状,这个桥洞的最大高度为16m,跨度为40m,现把它的示意图放在如图的平面直角坐标系中,则抛物线对应的函数关系式为
.
14.某厂生产某种零件,该厂为鼓励销售商订货,提供了如下信息:
①每个零件的成本价为40元;
②若订购量不超过100个,出厂价为60元;若订购量超过100个时,每多订1个,订购的全部零件的出厂单价就降低0.02元;
③实际出厂单价不能低于51元.
根据以上信息,解答下列问题:
(1)当一次订购量为
个时,零件的实际出厂单价降为51元.
(2)设一次订购量为x个时,零件的实际出厂单价为P元,写出P与x的函数表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂价﹣成本).
五.二次函数的应用
15.竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=﹣5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A.23.5m
B.22.5m
C.21.5m
D.20.5m
16.已知关于x的二次三项式(m+1)x2﹣(2m﹣1)x+m的值恒为正,则m的取值范围是( )
A.且m≠
B.m>﹣1
C.﹣1<m<
D.<m<1
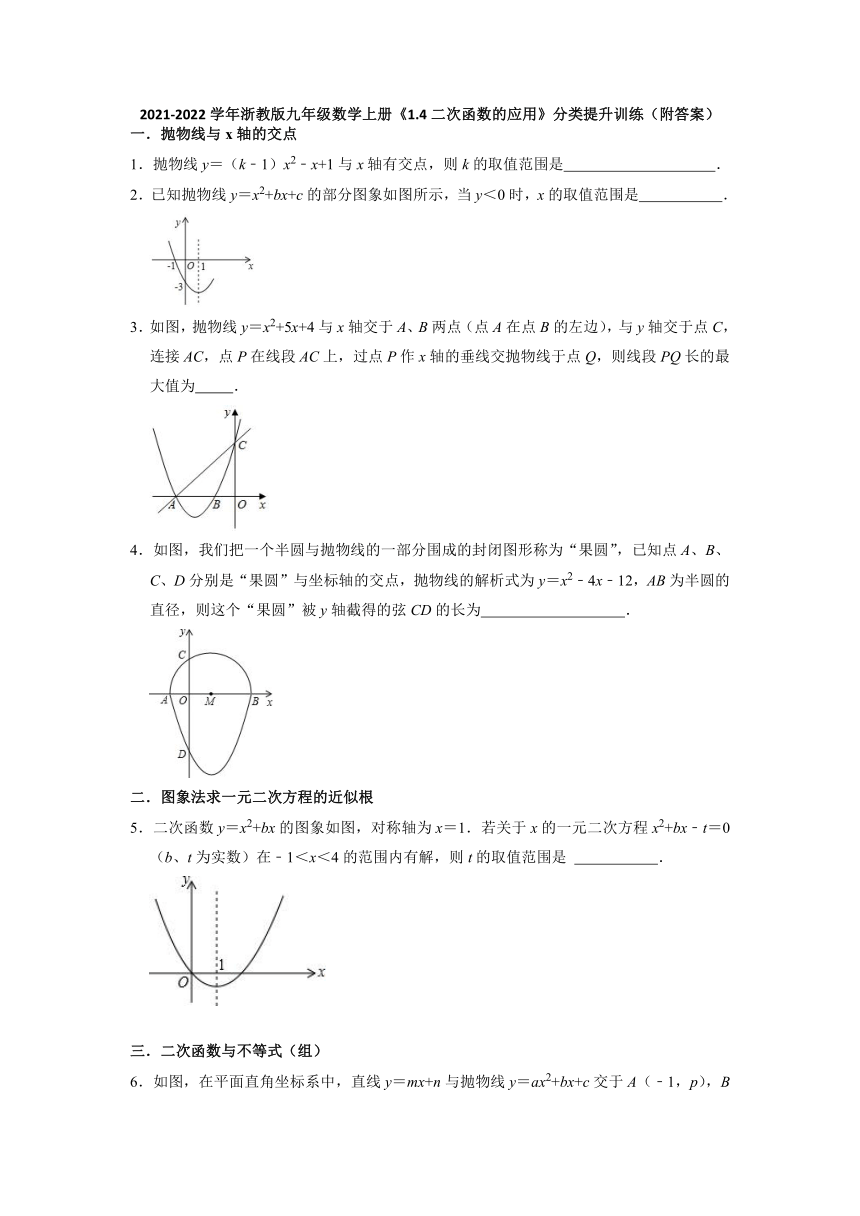
17.如图1,剪刀式升降平台由三个边长为4m的菱形和两个腰长为4m的等腰三角形组成,其中,AM∥A0N,B,B0在AM和A0N上可以滑动,A1、C1、B0始终在同一条直线上.
(1)这种升降平台设计原理利用了四边形的
性质;
(2)如图2是一个抛物线型的拱状建筑物,其底部最大跨度为8米,顶部的最大高度为24米.如图3,当该平台在完成挂横幅作业时,其顶部A,M两点恰好同时抵住抛物线,且AM=8米,则此时∠B1的度数为
.
18.如图是一座截面边缘为抛物线的拱形桥,当拱顶离水面2米高时,水面l为4米,则当水面下降1米时,水面宽度增加
米.
19.为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为60m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则BC长为
时,能围成的矩形区域ABCD的面积最大.
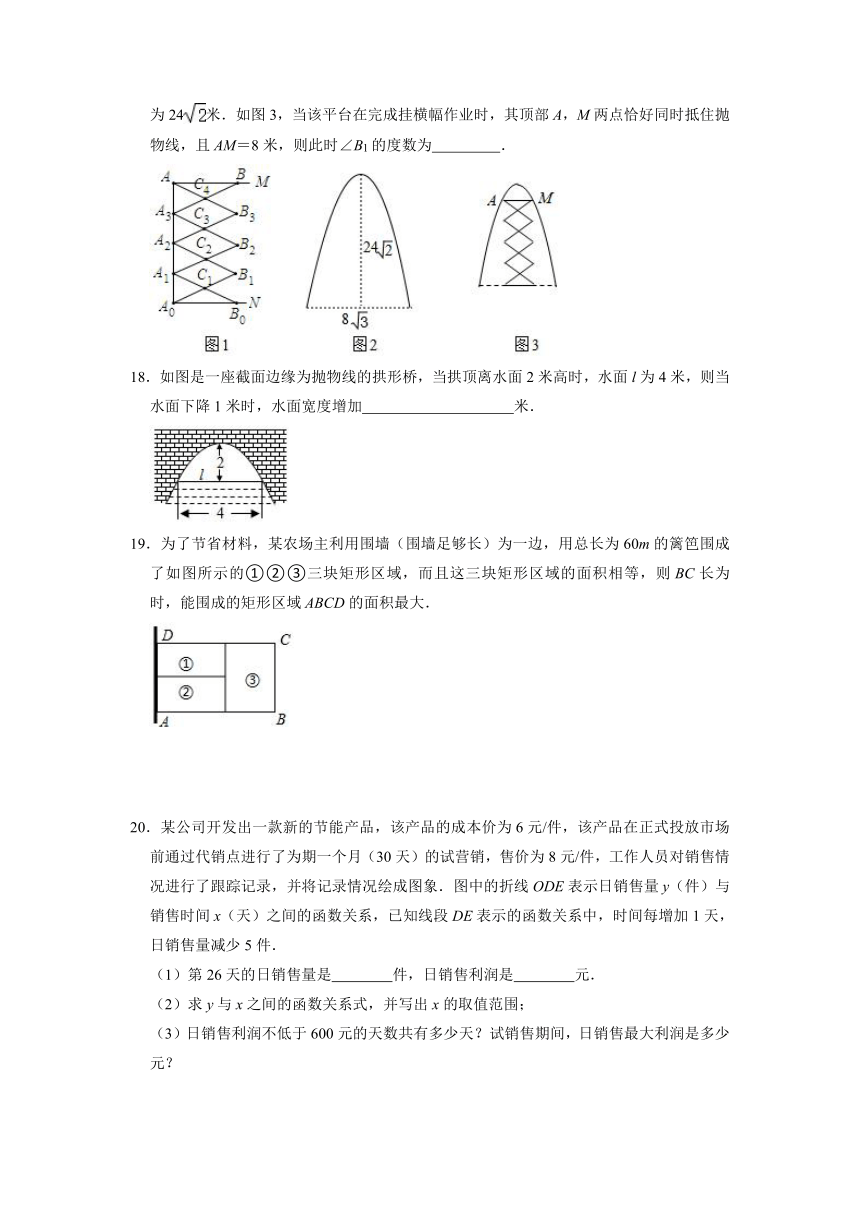
20.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象.图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第26天的日销售量是
件,日销售利润是
元.
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于600元的天数共有多少天?试销售期间,日销售最大利润是多少元?
六.二次函数综合题(共5小题)
21.如图,点E、F、G、H分别是正方形ABCD边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( )
A.B.C.D.
22.边长为1的正方形OA1B1C1的顶点A1在X轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为
.
23.如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(﹣1,﹣2)、(1,﹣2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
A.﹣3
B.﹣1
C.1
D.3
24.已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连接OA、OP.当OA⊥OP时,P点坐标为
.
25.已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧抛物线上找一点P,使得P、D、C构成以PC为底边的等腰三角形,求出点P的坐标及此时四边形PBCD的面积.
参考答案
一.抛物线与x轴的交点
1.解:∵抛物线y=(k﹣1)x2﹣x+1与x轴有交点,
∴△=(﹣1)2﹣4×(k﹣1)×1≥0,解得k≤,
又∵k﹣1≠0,
∴k≠1,
∴k的取值范围是k≤且k≠1;
故答案为:k≤且k≠1.
2.解:由图象可得,
该抛物线的对称轴为直线x=1,与x轴的一个交点为(﹣1,0),
故抛物线与x轴的另一个交点为(3,0),
故当y<0时,x的取值范围是﹣1<x<3.
3.解:当y=0时,x2+5x+4=0,解得x1=﹣4,x2=﹣1,则A(﹣4,0),B(﹣1,0),
当x=0时,y=x2+5x+4=4,则C(0,4),
设直线AC的解析式为y=kx+b,
把A(﹣4,0),C(0,4)代入得,解得,
∴直线AC的解析式为y=x+4,
设P(t,t+4)(﹣4≤t≤0),则Q(t,t2+5t+4),
∴PQ=t+4﹣(t2+5t+4)
=﹣t2﹣4t
=﹣(t+2)2+4,
∴当t=﹣2时,PQ有最大值,最大值为4.
故答案为4.
4.解:如图:连接CM,
当y=0时y=x2﹣4x﹣12=0,
解得x1=﹣2,x2=6,
∴A(﹣2,0),B(6,0),
∴AB=8,
又∵M为AB的中点,
∴M(2,0),
∴OM=2,CM=4,
∴CO=2,
当x=0时y=﹣12,所以OD=12,
∴CD=12+2,
故答案为12+2.
二.图象法求一元二次方程的近似根
5.解:对称轴为直线x=﹣=1,
解得b=﹣2,
所以,二次函数解析式为y=x2﹣2x,
y=(x﹣1)2﹣1,
x=﹣1时,y=1+2=3,
x=4时,y=16﹣2×4=8,
∵x2+bx﹣t=0相当于y=x2+bx与直线y=t的交点的横坐标,
∴当﹣1≤t<8时,在﹣1<x<4的范围内有解.
故答案为:﹣1≤t<8.
三.二次函数与不等式(组)
6.解:观察函数图象可知:当x<﹣1或x>2时,直线y=mx+n在抛物线y=ax2+bx+c的上方,
∴不等式mx+n>ax2+bx+c的解集为x<﹣1或x>2.
故选:D.
四.根据实际问题列二次函数关系式
7.解:设二次函数的解析式为:y=ax2+bx+c,
∵当x=55,75,80时,y=1800,1800,1550,
∴,
解得,
∴y与x的函数关系式是y=﹣2x2+260x﹣6450=﹣2(x﹣65)2+2000,
故选:D.
8.解:∵∠C=90°,BC=a,AC=b,AB=c,
∴a2+b2=c2,
∵Rt△ABC的面积S,
∴S=ab,
∵a+b=5,
∴(a+b)2=25,
∴a2+b2+2ab=25,
∴c2+4S=25,
∴S=.
故选:A.
9.解:设饲养室长为xm,占地面积为ym2,
则y关于x的函数表达式是:y=x (50+2﹣x)=﹣x2+26x.
故选:D.
10.解:∵矩形ABCD的两条对称轴为坐标轴,
∴矩形ABCD关于坐标原点对称,
∵A点C点是对角线上的两个点,
∴A点、C点关于坐标原点对称,
∴C点坐标为(﹣2,﹣1);
∴透明纸由A点平移至C点,抛物线向左平移了4个单位,向下平移了2个单位;
∵透明纸经过A点时,函数表达式为y=x2,
∴透明纸经过C点时,函数表达式为y=(x+4)2﹣2=x2+8x+14
故选:B.
11.解:y与x之间的关系应表示为:y=20+20(x+1)+20(x+1)2.
故答案为:y=20+20(x+1)+20(x+1)2.
12.解:设每块滑板降价x元,商店一星期销售这种滑板的利润是y元,
则y与x之间的函数表达式为:
y=(30﹣x)(80+4x)
=﹣4x2+40x+2400.
故答案为:y=﹣4x2+40x+2400.
13.解:设y=a(x﹣20)2+16,
因为抛物线过(0,0),
所以代入得:
400a+16=0,
解得a=﹣,
故此抛物线的函数关系式为:
y=﹣(x﹣20)2+16.
故答案为:y=﹣(x﹣20)2+16.
14.解:(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为x个,则x=100+=550,
根据实际出厂单价不能低于51元,
因此,当一次订购量为大于等于550个时,每个零件的实际出厂价恰好降为51元.
故答案为:≥550;
(2)当0<x≤100时,P=60
当100<x<550时,P=60﹣0.02(x﹣100)=62﹣
当x≥550时,P=51
所以P=;
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,
则L=(P﹣40)x=
当x=500时,L=22×500﹣=6000(元);当x=1000时,L=(51﹣40)×1000=11000(元),
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;如果订购1000个,利润是11000元.
五.二次函数的应用
15.解:由题意可得,
h=﹣5t2+20t+1.5=﹣5(t﹣2)2+21.5,
因为a=﹣5<0,
故当t=2时,h取得最大值,此时h=21.5,
故选:C.
16.解:设y=(m+1)x2﹣(2m﹣1)x+m,
∵二次三项式(m+1)x2﹣(2m﹣1)x+m的值恒为正,
∴(m+1)x2﹣(2m﹣1)x+m>0且2m﹣1≠0,
∴在函数y=(m+1)x2﹣(2m﹣1)x+m中,m+1>0且△=[﹣(2m﹣1)]2﹣4(m+1) m<0且2m﹣1≠0,
解得,m>且m≠,
故选:A.
17.解:(1)这种升降平台设计原理利用了四边形的具有不稳定性.
故答案为:不稳定性;
(2)以地面为x轴,顶部所在垂直于地面的直线为y轴,建立平面直角坐标系,
设y=ax2+24,
∵点(4,0)在该抛物线上,
∴0=a×(4)2+24,
解得,a=,
∴y=﹣x2+24,
当x=﹣4时,y=﹣×(﹣4)2+24=16,
∴菱形竖直的对角线长为16÷4=4,
又∵菱形的边长为4,42+42=(4)2,
∴∠B1=90°,
故答案为:90°.
18.解:建立平面直角坐标系如图:
则抛物线顶点C坐标为(0,2),
设抛物线解析式y=ax2+2,
将A点坐标(﹣2,0)代入,可得:0=4a+2,
解得:a=﹣,
故抛物线解析式为y=﹣x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,
也就是直线y=﹣1与抛物线相交的两点之间的距离,
将y=﹣1代入抛物线解析式得出:﹣1=﹣0.5x2+2,
解得:x=±,
所以水面宽度为2米,
故水面宽度增加了(2﹣4)米,
故答案为:(2﹣4).
19.解:如图,
∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE
面积的2倍,
∴AE=2BE,
设
BC=x(m),BE=FC=a(m),则AE=HG=DF=2a(m),
∴DF+FC+HG+AE+EB+EF+BC=60(m),即
8a+2x=60,
∴a=﹣x+,3a=﹣x+,
∴矩形区域
ABCD
的面积
S=(﹣x+)x=﹣x2+x,
∵a=﹣x+
∴x<30,
则
S=﹣x2+x
(0<x<30)
∵二次项系数为﹣<0
∴当x=﹣=15(m)时,S
有最大值,最大值为:﹣×152+×15=(m2)
故答案为:15m.
20.解:(1)340﹣(26﹣22)×5=320(件),
320×(8﹣6)=640(元).
故答案为:320;640;
(2)设线段OD所表示的y与x之间的函数关系式为y=kx,
将(17,340)代入y=kx中,
340=17k,解得:k=20,
∴线段OD所表示的y与x之间的函数关系式为y=20x.
根据题意得:线段DE所表示的y与x之间的函数关系式为y=340﹣5(x﹣22)=﹣5x+450.
联立两线段所表示的函数关系式成方程组,
得,解得:,
∴交点D的坐标为(18,360),
∴y与x之间的函数关系式为y=;
(3)当0≤x≤18时,根据题意得:(8﹣6)×20x≥600,
解得:x≥15;
当18<x≤30时,根据题意得:(8﹣6)×(﹣5x+450)≥600,
解得:x≤30.
∴15≤x≤30.
30﹣15+1=16(天),
∴日销售利润不低于600元的天数共有16天.
∵点D的坐标为(18,360),
∴日最大销售量为360件,
360×2=720(元),
∴试销售期间,日销售最大利润是720元.
六.二次函数综合题
21.解:设正方形的边长为m,则m>0,
∵AE=x,
∴DH=x,
∴AH=m﹣x,
∵EH2=AE2+AH2,
∴y=x2+(m﹣x)2,
y=x2+x2﹣2mx+m2,
y=2x2﹣2mx+m2,
=2[(x﹣m)2+],
=2(x﹣m)2+m2,
∴y与x的函数图象是A.
故选:A.
22.解:连接OB,
∵旋转75°,
∴x轴正半轴与OA的夹角为75°,
∵∠AOB=45°,
∴OB与x轴正半轴夹角为75°﹣45°=30°,
过B作BD⊥x轴于D,
∵BC=OC=1,∴OB=,
∴BD=,
∴OD=,
∴B(,),
把B点坐标代入y=ax2中得:,
解之得:a=.
23.解:根据题意知,点B的横坐标的最大值为3,
即可知当对称轴过N点时,点B的横坐标最大,
此时的A点坐标为(﹣1,0),
当可知当对称轴过M点时,点A的横坐标最小,此时的B点坐标为(1,0),
此时A点的坐标最小为(﹣3,0),
故点A的横坐标的最小值为﹣3,
故选:A.
24.解:∵抛物线y=ax2+x的对称轴为直线x=2,
∴﹣=2,
∴a=﹣,
∴抛物线的表达式为:y=﹣x2+x,
∴顶点A的坐标为(2,1),
设对称轴与x轴的交点为E.
如图,在直角三角形AOE和直角三角形POE中,
∵OA⊥OP,
∴∠OAE=∠EOP,
∵AE=1,OE=2,
∴=,
解得PE=4,
∴P(2,﹣4),
故答案为:(2,﹣4).
25.解:(1)∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C
(0,3),
∴,
∴,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),
∵y=﹣x2+2x+3与x轴交于另一点B,
∴令y=0,﹣x2+2x+3=0,解得x=﹣1或3,
∴A(﹣1,0),B(3,0),
∴CD==,
BC==3,
BD==2,
∵CD2+BC2=()2+(3)2=20,BD2=(2)2=20,
∴CD2+BC2=BD2,
∴△BCD是直角三角形;
(3)如图,
∵P、D、C构成以PC为底边的等腰三角形,
∴点D在PC的垂直平分线上,
∴点C与点P关于对称轴直线x=1对称,
∴点P的坐标为(2,3),
∵S四边形PBCD=S△DCP+S△CBP,
∴S四边形PBCD=×2×(4﹣3)+×2×3=4
一.抛物线与x轴的交点
1.抛物线y=(k﹣1)x2﹣x+1与x轴有交点,则k的取值范围是
.
2.已知抛物线y=x2+bx+c的部分图象如图所示,当y<0时,x的取值范围是
.
3.如图,抛物线y=x2+5x+4与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接AC,点P在线段AC上,过点P作x轴的垂线交抛物线于点Q,则线段PQ长的最大值为
.
4.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣4x﹣12,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为
.
二.图象法求一元二次方程的近似根
5.二次函数y=x2+bx的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx﹣t=0(b、t为实数)在﹣1<x<4的范围内有解,则t的取值范围是
.
三.二次函数与不等式(组)
6.如图,在平面直角坐标系中,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(2,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是( )
A.x<﹣1
B.x>2
C.﹣1<x<2
D.x<﹣1或x>2
四.根据实际问题列二次函数关系式
7.记某商品销售单价为x元,商家销售此种商品每月获得的销售利润为y元,且y是关于x的二次函数.已知当商家将此种商品销售单价分别定为55元或75元时,他每月均可获得销售利润1800元;当商家将此种商品销售单价定为80元时,他每月可获得销售利润1550元,则y与x的函数关系式是( )
A.y=﹣(x﹣60)2+1825
B.y=﹣2(x﹣60)2+1850
C.y=﹣(x﹣65)2+1900
D.y=﹣2(x﹣65)2+2000
8.在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,若a+b=5,则Rt△ABC的面积S关于边长c的函数关系式为( )
A.S=
B.S=
C.S=
D.S=
9.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门,已知计划中的建筑材料可建围墙(不包括门)的总长度为50m.设饲养室长为xm,占地面积为ym2,则y关于x的函数表达式是( )
A.y=﹣x2+50x
B.y=﹣x2+24x
C.y=﹣x2+25x
D.y=﹣x2+26x
10.矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点于点C重合,则该抛物线的函数表达式变为( )
A.y=x2﹣8x+14
B.y=x2+8x+14
C.y=x2+4x+3
D.y=x2﹣4x+3
11.某工厂今年一月份生产防疫护目镜的产量是20万件,计划之后两个月增加产量,如果月平均增长率为x,那么第一季度防疫护目镜的产量y(万件)与x之间的关系应表示为
.
12.某体育用品商店购进一批滑板,每块滑板利润为30元,一星期可卖出80块.商家决定降价促销,根据市场调查,每降价1元,则一星期可多卖出4块.设每块滑板降价x元,商店一星期销售这种滑板的利润是y元,则y与x之间的函数表达式为
.
13.如图,有一座拱桥洞呈抛物线形状,这个桥洞的最大高度为16m,跨度为40m,现把它的示意图放在如图的平面直角坐标系中,则抛物线对应的函数关系式为
.
14.某厂生产某种零件,该厂为鼓励销售商订货,提供了如下信息:
①每个零件的成本价为40元;
②若订购量不超过100个,出厂价为60元;若订购量超过100个时,每多订1个,订购的全部零件的出厂单价就降低0.02元;
③实际出厂单价不能低于51元.
根据以上信息,解答下列问题:
(1)当一次订购量为
个时,零件的实际出厂单价降为51元.
(2)设一次订购量为x个时,零件的实际出厂单价为P元,写出P与x的函数表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂价﹣成本).
五.二次函数的应用
15.竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=﹣5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )
A.23.5m
B.22.5m
C.21.5m
D.20.5m
16.已知关于x的二次三项式(m+1)x2﹣(2m﹣1)x+m的值恒为正,则m的取值范围是( )
A.且m≠
B.m>﹣1
C.﹣1<m<
D.<m<1
17.如图1,剪刀式升降平台由三个边长为4m的菱形和两个腰长为4m的等腰三角形组成,其中,AM∥A0N,B,B0在AM和A0N上可以滑动,A1、C1、B0始终在同一条直线上.
(1)这种升降平台设计原理利用了四边形的
性质;
(2)如图2是一个抛物线型的拱状建筑物,其底部最大跨度为8米,顶部的最大高度为24米.如图3,当该平台在完成挂横幅作业时,其顶部A,M两点恰好同时抵住抛物线,且AM=8米,则此时∠B1的度数为
.
18.如图是一座截面边缘为抛物线的拱形桥,当拱顶离水面2米高时,水面l为4米,则当水面下降1米时,水面宽度增加
米.
19.为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为60m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则BC长为
时,能围成的矩形区域ABCD的面积最大.
20.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象.图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第26天的日销售量是
件,日销售利润是
元.
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于600元的天数共有多少天?试销售期间,日销售最大利润是多少元?
六.二次函数综合题(共5小题)
21.如图,点E、F、G、H分别是正方形ABCD边AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能为( )
A.B.C.D.
22.边长为1的正方形OA1B1C1的顶点A1在X轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为
.
23.如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(﹣1,﹣2)、(1,﹣2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
A.﹣3
B.﹣1
C.1
D.3
24.已知:如图,在平面直角坐标系中,抛物线y=ax2+x的对称轴为直线x=2,顶点为A.点P为抛物线对称轴上一点,连接OA、OP.当OA⊥OP时,P点坐标为
.
25.已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧抛物线上找一点P,使得P、D、C构成以PC为底边的等腰三角形,求出点P的坐标及此时四边形PBCD的面积.
参考答案
一.抛物线与x轴的交点
1.解:∵抛物线y=(k﹣1)x2﹣x+1与x轴有交点,
∴△=(﹣1)2﹣4×(k﹣1)×1≥0,解得k≤,
又∵k﹣1≠0,
∴k≠1,
∴k的取值范围是k≤且k≠1;
故答案为:k≤且k≠1.
2.解:由图象可得,
该抛物线的对称轴为直线x=1,与x轴的一个交点为(﹣1,0),
故抛物线与x轴的另一个交点为(3,0),
故当y<0时,x的取值范围是﹣1<x<3.
3.解:当y=0时,x2+5x+4=0,解得x1=﹣4,x2=﹣1,则A(﹣4,0),B(﹣1,0),
当x=0时,y=x2+5x+4=4,则C(0,4),
设直线AC的解析式为y=kx+b,
把A(﹣4,0),C(0,4)代入得,解得,
∴直线AC的解析式为y=x+4,
设P(t,t+4)(﹣4≤t≤0),则Q(t,t2+5t+4),
∴PQ=t+4﹣(t2+5t+4)
=﹣t2﹣4t
=﹣(t+2)2+4,
∴当t=﹣2时,PQ有最大值,最大值为4.
故答案为4.
4.解:如图:连接CM,
当y=0时y=x2﹣4x﹣12=0,
解得x1=﹣2,x2=6,
∴A(﹣2,0),B(6,0),
∴AB=8,
又∵M为AB的中点,
∴M(2,0),
∴OM=2,CM=4,
∴CO=2,
当x=0时y=﹣12,所以OD=12,
∴CD=12+2,
故答案为12+2.
二.图象法求一元二次方程的近似根
5.解:对称轴为直线x=﹣=1,
解得b=﹣2,
所以,二次函数解析式为y=x2﹣2x,
y=(x﹣1)2﹣1,
x=﹣1时,y=1+2=3,
x=4时,y=16﹣2×4=8,
∵x2+bx﹣t=0相当于y=x2+bx与直线y=t的交点的横坐标,
∴当﹣1≤t<8时,在﹣1<x<4的范围内有解.
故答案为:﹣1≤t<8.
三.二次函数与不等式(组)
6.解:观察函数图象可知:当x<﹣1或x>2时,直线y=mx+n在抛物线y=ax2+bx+c的上方,
∴不等式mx+n>ax2+bx+c的解集为x<﹣1或x>2.
故选:D.
四.根据实际问题列二次函数关系式
7.解:设二次函数的解析式为:y=ax2+bx+c,
∵当x=55,75,80时,y=1800,1800,1550,
∴,
解得,
∴y与x的函数关系式是y=﹣2x2+260x﹣6450=﹣2(x﹣65)2+2000,
故选:D.
8.解:∵∠C=90°,BC=a,AC=b,AB=c,
∴a2+b2=c2,
∵Rt△ABC的面积S,
∴S=ab,
∵a+b=5,
∴(a+b)2=25,
∴a2+b2+2ab=25,
∴c2+4S=25,
∴S=.
故选:A.
9.解:设饲养室长为xm,占地面积为ym2,
则y关于x的函数表达式是:y=x (50+2﹣x)=﹣x2+26x.
故选:D.
10.解:∵矩形ABCD的两条对称轴为坐标轴,
∴矩形ABCD关于坐标原点对称,
∵A点C点是对角线上的两个点,
∴A点、C点关于坐标原点对称,
∴C点坐标为(﹣2,﹣1);
∴透明纸由A点平移至C点,抛物线向左平移了4个单位,向下平移了2个单位;
∵透明纸经过A点时,函数表达式为y=x2,
∴透明纸经过C点时,函数表达式为y=(x+4)2﹣2=x2+8x+14
故选:B.
11.解:y与x之间的关系应表示为:y=20+20(x+1)+20(x+1)2.
故答案为:y=20+20(x+1)+20(x+1)2.
12.解:设每块滑板降价x元,商店一星期销售这种滑板的利润是y元,
则y与x之间的函数表达式为:
y=(30﹣x)(80+4x)
=﹣4x2+40x+2400.
故答案为:y=﹣4x2+40x+2400.
13.解:设y=a(x﹣20)2+16,
因为抛物线过(0,0),
所以代入得:
400a+16=0,
解得a=﹣,
故此抛物线的函数关系式为:
y=﹣(x﹣20)2+16.
故答案为:y=﹣(x﹣20)2+16.
14.解:(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为x个,则x=100+=550,
根据实际出厂单价不能低于51元,
因此,当一次订购量为大于等于550个时,每个零件的实际出厂价恰好降为51元.
故答案为:≥550;
(2)当0<x≤100时,P=60
当100<x<550时,P=60﹣0.02(x﹣100)=62﹣
当x≥550时,P=51
所以P=;
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,
则L=(P﹣40)x=
当x=500时,L=22×500﹣=6000(元);当x=1000时,L=(51﹣40)×1000=11000(元),
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;如果订购1000个,利润是11000元.
五.二次函数的应用
15.解:由题意可得,
h=﹣5t2+20t+1.5=﹣5(t﹣2)2+21.5,
因为a=﹣5<0,
故当t=2时,h取得最大值,此时h=21.5,
故选:C.
16.解:设y=(m+1)x2﹣(2m﹣1)x+m,
∵二次三项式(m+1)x2﹣(2m﹣1)x+m的值恒为正,
∴(m+1)x2﹣(2m﹣1)x+m>0且2m﹣1≠0,
∴在函数y=(m+1)x2﹣(2m﹣1)x+m中,m+1>0且△=[﹣(2m﹣1)]2﹣4(m+1) m<0且2m﹣1≠0,
解得,m>且m≠,
故选:A.
17.解:(1)这种升降平台设计原理利用了四边形的具有不稳定性.
故答案为:不稳定性;
(2)以地面为x轴,顶部所在垂直于地面的直线为y轴,建立平面直角坐标系,
设y=ax2+24,
∵点(4,0)在该抛物线上,
∴0=a×(4)2+24,
解得,a=,
∴y=﹣x2+24,
当x=﹣4时,y=﹣×(﹣4)2+24=16,
∴菱形竖直的对角线长为16÷4=4,
又∵菱形的边长为4,42+42=(4)2,
∴∠B1=90°,
故答案为:90°.
18.解:建立平面直角坐标系如图:
则抛物线顶点C坐标为(0,2),
设抛物线解析式y=ax2+2,
将A点坐标(﹣2,0)代入,可得:0=4a+2,
解得:a=﹣,
故抛物线解析式为y=﹣x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,
也就是直线y=﹣1与抛物线相交的两点之间的距离,
将y=﹣1代入抛物线解析式得出:﹣1=﹣0.5x2+2,
解得:x=±,
所以水面宽度为2米,
故水面宽度增加了(2﹣4)米,
故答案为:(2﹣4).
19.解:如图,
∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE
面积的2倍,
∴AE=2BE,
设
BC=x(m),BE=FC=a(m),则AE=HG=DF=2a(m),
∴DF+FC+HG+AE+EB+EF+BC=60(m),即
8a+2x=60,
∴a=﹣x+,3a=﹣x+,
∴矩形区域
ABCD
的面积
S=(﹣x+)x=﹣x2+x,
∵a=﹣x+
∴x<30,
则
S=﹣x2+x
(0<x<30)
∵二次项系数为﹣<0
∴当x=﹣=15(m)时,S
有最大值,最大值为:﹣×152+×15=(m2)
故答案为:15m.
20.解:(1)340﹣(26﹣22)×5=320(件),
320×(8﹣6)=640(元).
故答案为:320;640;
(2)设线段OD所表示的y与x之间的函数关系式为y=kx,
将(17,340)代入y=kx中,
340=17k,解得:k=20,
∴线段OD所表示的y与x之间的函数关系式为y=20x.
根据题意得:线段DE所表示的y与x之间的函数关系式为y=340﹣5(x﹣22)=﹣5x+450.
联立两线段所表示的函数关系式成方程组,
得,解得:,
∴交点D的坐标为(18,360),
∴y与x之间的函数关系式为y=;
(3)当0≤x≤18时,根据题意得:(8﹣6)×20x≥600,
解得:x≥15;
当18<x≤30时,根据题意得:(8﹣6)×(﹣5x+450)≥600,
解得:x≤30.
∴15≤x≤30.
30﹣15+1=16(天),
∴日销售利润不低于600元的天数共有16天.
∵点D的坐标为(18,360),
∴日最大销售量为360件,
360×2=720(元),
∴试销售期间,日销售最大利润是720元.
六.二次函数综合题
21.解:设正方形的边长为m,则m>0,
∵AE=x,
∴DH=x,
∴AH=m﹣x,
∵EH2=AE2+AH2,
∴y=x2+(m﹣x)2,
y=x2+x2﹣2mx+m2,
y=2x2﹣2mx+m2,
=2[(x﹣m)2+],
=2(x﹣m)2+m2,
∴y与x的函数图象是A.
故选:A.
22.解:连接OB,
∵旋转75°,
∴x轴正半轴与OA的夹角为75°,
∵∠AOB=45°,
∴OB与x轴正半轴夹角为75°﹣45°=30°,
过B作BD⊥x轴于D,
∵BC=OC=1,∴OB=,
∴BD=,
∴OD=,
∴B(,),
把B点坐标代入y=ax2中得:,
解之得:a=.
23.解:根据题意知,点B的横坐标的最大值为3,
即可知当对称轴过N点时,点B的横坐标最大,
此时的A点坐标为(﹣1,0),
当可知当对称轴过M点时,点A的横坐标最小,此时的B点坐标为(1,0),
此时A点的坐标最小为(﹣3,0),
故点A的横坐标的最小值为﹣3,
故选:A.
24.解:∵抛物线y=ax2+x的对称轴为直线x=2,
∴﹣=2,
∴a=﹣,
∴抛物线的表达式为:y=﹣x2+x,
∴顶点A的坐标为(2,1),
设对称轴与x轴的交点为E.
如图,在直角三角形AOE和直角三角形POE中,
∵OA⊥OP,
∴∠OAE=∠EOP,
∵AE=1,OE=2,
∴=,
解得PE=4,
∴P(2,﹣4),
故答案为:(2,﹣4).
25.解:(1)∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C
(0,3),
∴,
∴,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),
∵y=﹣x2+2x+3与x轴交于另一点B,
∴令y=0,﹣x2+2x+3=0,解得x=﹣1或3,
∴A(﹣1,0),B(3,0),
∴CD==,
BC==3,
BD==2,
∵CD2+BC2=()2+(3)2=20,BD2=(2)2=20,
∴CD2+BC2=BD2,
∴△BCD是直角三角形;
(3)如图,
∵P、D、C构成以PC为底边的等腰三角形,
∴点D在PC的垂直平分线上,
∴点C与点P关于对称轴直线x=1对称,
∴点P的坐标为(2,3),
∵S四边形PBCD=S△DCP+S△CBP,
∴S四边形PBCD=×2×(4﹣3)+×2×3=4
同课章节目录
