浙教版数学八下第5章特殊四边形练习题(word版、无答案)
文档属性
| 名称 | 浙教版数学八下第5章特殊四边形练习题(word版、无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 105.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 17:20:01 | ||
图片预览

文档简介
特殊平行四边形
1.
如图,在矩形ABCD中,对角线AC,
BD相交于点O,点E,
F分别是AO,
AD的中点,连接EF,若AB=6
cm,
BC=8
cm,则EF的长是
2.
如图,四边形ABCO是矩形,点D是BC边上的动点(点D与点B、点C不重合),则的值为( )
A.
1
B.
C.
2
D.
无法确定
3
如图,在矩形ABCD中,AB=3,
BC=10,
点E在BC边上,DF⊥AE,垂足为F.若DF=6,则线段EF的长为( )
A.
2
B.
3
C.
4
D.
5
4.
如图,在矩形ABCD中,AB=6,
BC=10,点E、F在AD边上,BF和CE交于点G,
若EF=AD,则图中阴影部分的面积为
5.
如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,若∠ADB=38°,则∠E=________.
6.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
7.如图,在矩形ABCD中,AB=4,BC=6,点E为边BC上一点,且EC=2BE,点F是CD的中点,点G为EF的中点,则EF的长为________,AG的长为________.
8.如图,将一张矩形纸片ABCD沿对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.过点D作DG∥BE,交BC于点G,连接FG交BD于点O.若AB=3,AD=4,则OB=________,FG=________.
9.
如图,点C在线段AB上,且AC=2BC,分别以AC、BC为边在线段AB的同侧作正方形ACDE、BCFG,连接EC、EG,则tan∠CEG=________.
10.
如图,在矩形ABCD中,E,F分别是AD,BC的中点,M是AF和BE的交点,N是CE和DF的交点.若四边形EMFN是正方形,则AB与BC之间的数量关系是________.
11.
如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为______.
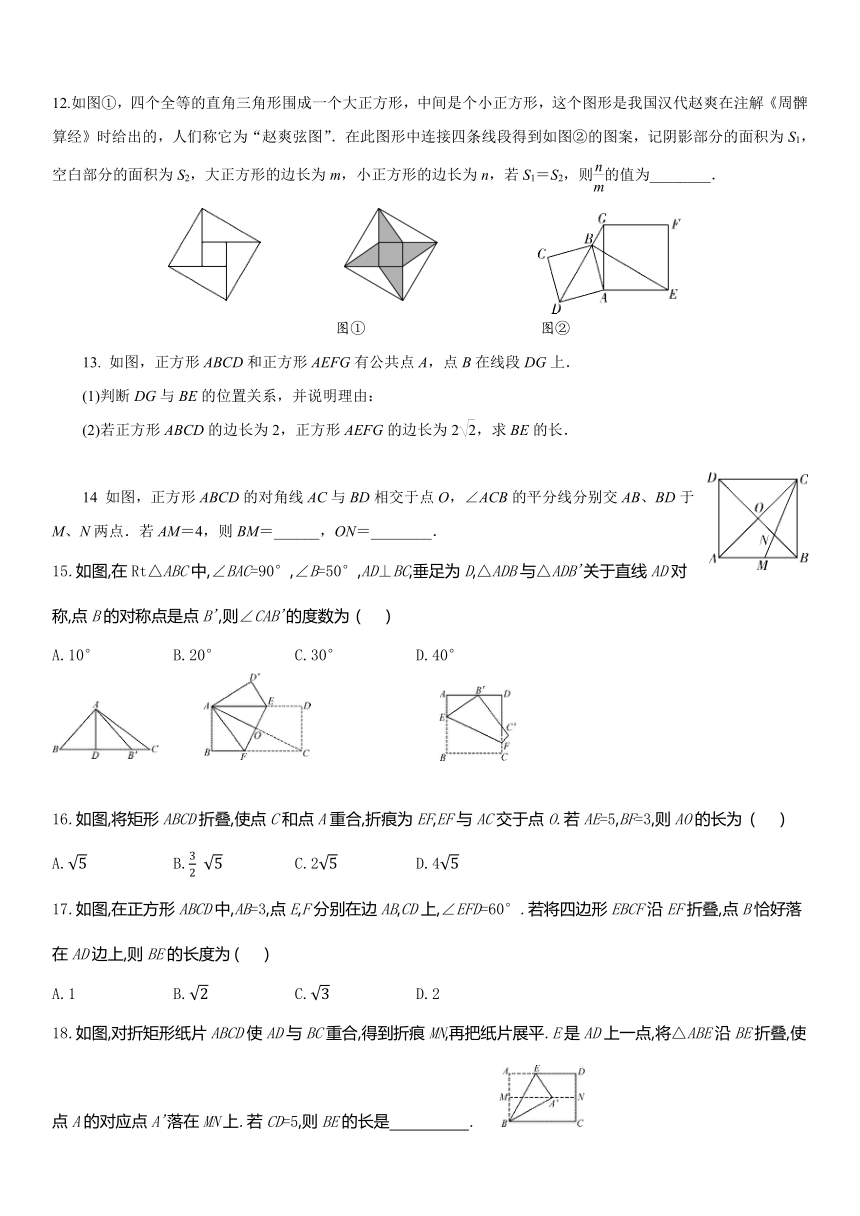
12.如图①,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图②的图案,记阴影部分的面积为S1,空白部分的面积为S2,大正方形的边长为m,小正方形的边长为n,若S1=S2,则的值为________.
图①
图②
13.
如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.
(1)判断DG与BE的位置关系,并说明理由:
(2)若正方形ABCD的边长为2,正方形AEFG的边长为2,求BE的长.
14
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的平分线分别交AB、BD于M、N两点.若AM=4,则BM=______,ON=________.
15.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为
(
)
A.10°
B.20°
C.30°
D.40°
16.如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=5,BF=3,则AO的长为
(
)
A.
B.
C.2
D.4
17.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为
(
)
A.1
B.
C.
D.2
18.如图,对折矩形纸片ABCD使AD与BC重合,得到折痕MN,再把纸片展平.E是AD上一点,将△ABE沿BE折叠,使点A的对应点A'落在MN上.若CD=5,则BE的长是 .
19.如图,在矩形ABCD中,BC=8,E为BC中点,将△ABE沿AE翻折后,得到△AEF,再将CE折向FE,使点C与点F重合,折痕为EG.
若CG=3,则AG= .
10.如图,△ABD中,∠ABD=∠ADB.
(1)作点A关于BD的对称点C.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)所作的图中,连结BC,DC,连结AC,交BD于点O.
①求证:四边形ABCD是菱形.
②取BC的中点E,连结OE,若OE=,BD=10,求点E到AD的距离.
21.如图,四边形ABCD是一张正方形纸片,其面积为25cm2.分别在边AB,BC,CD,DA上顺次截取AE=BF=CG=DH=acm(AE>BE),连结EF,FG,GH,HE.分别以EF,FG,GH,HE为轴将纸片向内翻折,得到四边形A1B1C1D1.若四边形A1B1C1D1的面积为9cm2,则a=
.
第12题图
22.如图1,已知四边形ABCD是正方形,将△DAE,△DCF分别沿DE,DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点).
(1)求∠EDF的度数.
(2)若GF=4,EG=6,求DG的长.
23.如图,在矩形ABCD中,AB=6,BC=8,对角线AC,BD相交于点O,点P为边AD上一动点,连结OP,以OP为折痕,将△AOP折叠,点A的对应点为点E,线段PE与OD相交于点F.若△PDF为直角三角形,求DP的长.
24.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为
.
25.如图,在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=3cm,则AC的长为
cm.
26.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是
(填序号).
27.如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连结EF.
(1)求证:AC⊥EF.
(2)延长EF交CD的延长线于点G,连结BD交AC于点O,若BD=4,tanG=,求AO的长.
1.
如图,在矩形ABCD中,对角线AC,
BD相交于点O,点E,
F分别是AO,
AD的中点,连接EF,若AB=6
cm,
BC=8
cm,则EF的长是
2.
如图,四边形ABCO是矩形,点D是BC边上的动点(点D与点B、点C不重合),则的值为( )
A.
1
B.
C.
2
D.
无法确定
3
如图,在矩形ABCD中,AB=3,
BC=10,
点E在BC边上,DF⊥AE,垂足为F.若DF=6,则线段EF的长为( )
A.
2
B.
3
C.
4
D.
5
4.
如图,在矩形ABCD中,AB=6,
BC=10,点E、F在AD边上,BF和CE交于点G,
若EF=AD,则图中阴影部分的面积为
5.
如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,若∠ADB=38°,则∠E=________.
6.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
7.如图,在矩形ABCD中,AB=4,BC=6,点E为边BC上一点,且EC=2BE,点F是CD的中点,点G为EF的中点,则EF的长为________,AG的长为________.
8.如图,将一张矩形纸片ABCD沿对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.过点D作DG∥BE,交BC于点G,连接FG交BD于点O.若AB=3,AD=4,则OB=________,FG=________.
9.
如图,点C在线段AB上,且AC=2BC,分别以AC、BC为边在线段AB的同侧作正方形ACDE、BCFG,连接EC、EG,则tan∠CEG=________.
10.
如图,在矩形ABCD中,E,F分别是AD,BC的中点,M是AF和BE的交点,N是CE和DF的交点.若四边形EMFN是正方形,则AB与BC之间的数量关系是________.
11.
如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为______.
12.如图①,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图②的图案,记阴影部分的面积为S1,空白部分的面积为S2,大正方形的边长为m,小正方形的边长为n,若S1=S2,则的值为________.
图①
图②
13.
如图,正方形ABCD和正方形AEFG有公共点A,点B在线段DG上.
(1)判断DG与BE的位置关系,并说明理由:
(2)若正方形ABCD的边长为2,正方形AEFG的边长为2,求BE的长.
14
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的平分线分别交AB、BD于M、N两点.若AM=4,则BM=______,ON=________.
15.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为
(
)
A.10°
B.20°
C.30°
D.40°
16.如图,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=5,BF=3,则AO的长为
(
)
A.
B.
C.2
D.4
17.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为
(
)
A.1
B.
C.
D.2
18.如图,对折矩形纸片ABCD使AD与BC重合,得到折痕MN,再把纸片展平.E是AD上一点,将△ABE沿BE折叠,使点A的对应点A'落在MN上.若CD=5,则BE的长是 .
19.如图,在矩形ABCD中,BC=8,E为BC中点,将△ABE沿AE翻折后,得到△AEF,再将CE折向FE,使点C与点F重合,折痕为EG.
若CG=3,则AG= .
10.如图,△ABD中,∠ABD=∠ADB.
(1)作点A关于BD的对称点C.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)所作的图中,连结BC,DC,连结AC,交BD于点O.
①求证:四边形ABCD是菱形.
②取BC的中点E,连结OE,若OE=,BD=10,求点E到AD的距离.
21.如图,四边形ABCD是一张正方形纸片,其面积为25cm2.分别在边AB,BC,CD,DA上顺次截取AE=BF=CG=DH=acm(AE>BE),连结EF,FG,GH,HE.分别以EF,FG,GH,HE为轴将纸片向内翻折,得到四边形A1B1C1D1.若四边形A1B1C1D1的面积为9cm2,则a=
.
第12题图
22.如图1,已知四边形ABCD是正方形,将△DAE,△DCF分别沿DE,DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点).
(1)求∠EDF的度数.
(2)若GF=4,EG=6,求DG的长.
23.如图,在矩形ABCD中,AB=6,BC=8,对角线AC,BD相交于点O,点P为边AD上一动点,连结OP,以OP为折痕,将△AOP折叠,点A的对应点为点E,线段PE与OD相交于点F.若△PDF为直角三角形,求DP的长.
24.如图,在菱形ABCD中,对角线AC,BD交于点O,其中OA=1,OB=2,则菱形ABCD的面积为
.
25.如图,在矩形ABCD中,对角线AC,BD相交于点O,已知∠BOC=120°,DC=3cm,则AC的长为
cm.
26.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是
(填序号).
27.如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连结EF.
(1)求证:AC⊥EF.
(2)延长EF交CD的延长线于点G,连结BD交AC于点O,若BD=4,tanG=,求AO的长.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
