第一章 二次函数单元测试题(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版2021年九年级(上)第一章《二次函数》专题训练
满分:120分
测试时间:120分钟
一.选择题(共10小题,每题3分,共30分)
1.下列函数中是二次函数的是
A.
B.
C.
D.
2.二次函数有
A.最大值
B.最小值
C.最大值7
D.最小值7
3.二次函数的顶点是
A.
B.
C.
D.
4.已知抛物线,则下列说法,错误的是
A.开口方向向下
B.顶点坐标是
C.对称轴是直线
D.当时,随的增大而减小
5.如图,二次函数使得的的取值范围是
A.或
B.
C.或
D.
6.二次函数,,是常数,且中的与的部分对应值如表所示,则下列结论中,正确的个数有
0
1
3
3
5
3
(1);(2)当时,;(3)当时,的值随值的增大而增大;
(4)方程有两个不相等是实数根.
A.4个
B.3个
C.2个
D.1个
7.如图是抛物线的部分图象,其顶点坐标为,且与轴的一个交点在点和之间,则下列结论中,其中正确的结论的个数是
①;②;③;④一元二次方程有两个不等实数根.
A.1
B.2
C.3
D.4
8.已知二次函数,当时,,则的值是
A.3
B.4
C.6
D.7
9.已知二次函数的图象交轴于,两点.若其图象上有且只有,,三点满足,则的值是
A.1
B.
C.2
D.4
10.将二次函数的图象在轴上方的部分沿轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,的值为
A.或
B.或
C.或
D.或
二.填空题(共6小题,每题4分,共24分)
11.若是二次函数,则 .
12.已知、是二次函数图象上的两个点,则与的大小关系为
.
13.若二次函数的图象与轴有两个不相同的交点,则的取值范围是
.
14.在综合实践活动中,同学们借助如图所示的直角墙角(两边足够长),用长的篱笆围成一个矩形花园,则矩形花园的最大面积为
.
15.已知抛物线,点在抛物线上,则的最大值是
.
16.已知二次函数(其中是自变量),当时,随的增大而减小,且时,的最大值为7,则的值为
.
三.解答题(共8小题,共66分)
17.(6分)已知二次函数的图象经过点,.
(1)试确定此二次函数的解析式;
(2)请你判断点是否在这个二次函数的图象上?
18.(6分)已知二次函数的图象经过点,.
(1)求该二次函数的解析式;
(2)在图中画出该函数的图象.
19.(6分)抛物线.
(1)
用配方法求顶点坐标,
对称轴;
(2)取何值时,随的增大而减小?
(3)取何值时,;取何值时,;取何值时,.
20.(8分)2019年春节期间某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于68元,经市场调查,每天的销售量(千克)与每千克售价(元满足一次函数关系,部分数据如下表:
售价(元千克)
50
55
60
销售量(千克)
100
90
80
(1)则与之间的函数表达式
.
(2)设这种商品每天的利润为(元,求与之间的函数表达式,并求出当售价为多少元时获得最大利润,最大利润是多少?(利润收入成本)
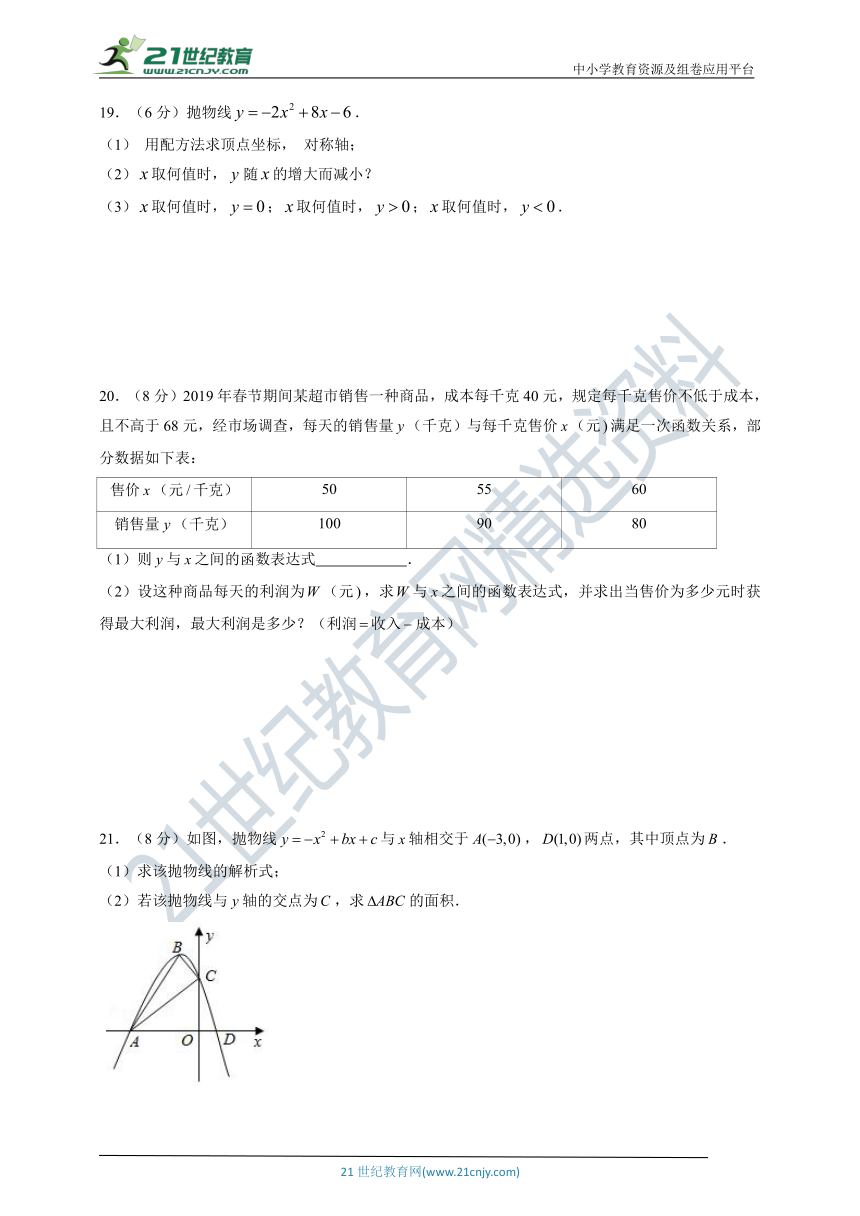
21.(8分)如图,抛物线与轴相交于,两点,其中顶点为.
(1)求该抛物线的解析式;
(2)若该抛物线与轴的交点为,求的面积.
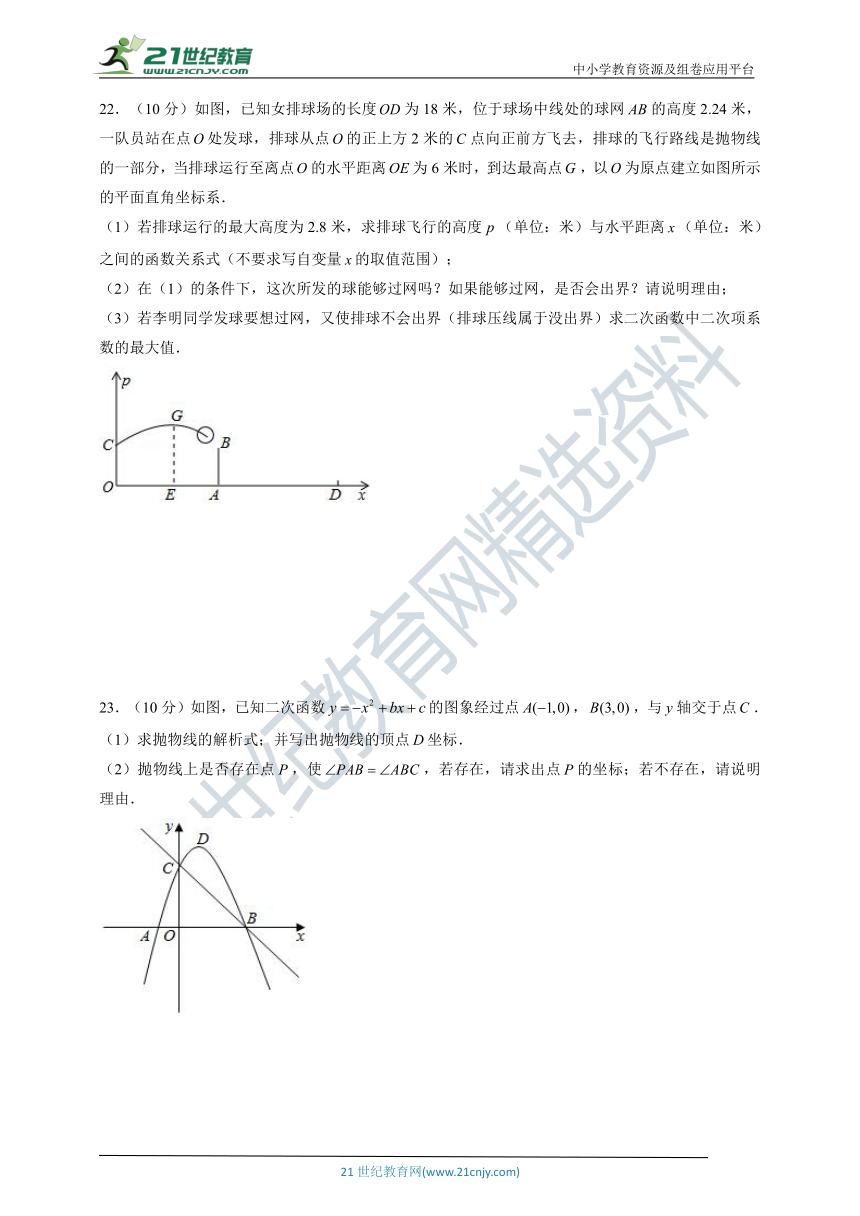
22.(10分)如图,已知女排球场的长度为18米,位于球场中线处的球网的高度2.24米,一队员站在点处发球,排球从点的正上方2米的点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点的水平距离为6米时,到达最高点,以为原点建立如图所示的平面直角坐标系.
(1)若排球运行的最大高度为2.8米,求排球飞行的高度(单位:米)与水平距离(单位:米)之间的函数关系式(不要求写自变量的取值范围);
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由;
(3)若李明同学发球要想过网,又使排球不会出界(排球压线属于没出界)求二次函数中二次项系数的最大值.
23.(10分)如图,已知二次函数的图象经过点,,与轴交于点.
(1)求抛物线的解析式;并写出抛物线的顶点坐标.
(2)抛物线上是否存在点,使,若存在,请求出点的坐标;若不存在,请说明理由.
24.(12分)已知,抛物线与轴交点为和点,与轴交点为,直线与抛物线的交点为点和点.
(1)求抛物线和直线的解析式;
(2)如图,点为抛物线上一动点(不与、重合),当点在直线下方时,过点作轴交于点,求的最大值;
(3)点为抛物线上一动点(不与、重合),为直线上一动点,是否存在点,使得以、、、为顶点的四边形是平行四边形?如果存在,请直接写出点的坐标,如果不存在,请说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.解:二次函数的解析式为,
.,自变量的最高次数是二次,是二次函数;
.,自变量的最高次数是一次,不是二次函数;
,自变量的的次数为次,不是二次函数;
,自变量的的次数为次,不是二次函数.
故选:.
2.解:二次函数中,,
二次函数,当时有最大值,
故选:.
3.解:二次函数,
该函数的顶点坐标为,
故选:.
4.解:、抛物线,,抛物线开口向下,此选项正确;
、抛物线顶点坐标是,此选项正确;
、抛物线对称轴,此选项正确.
、抛物线的对称轴为,开口向下,当时,随的增大而增大,此选项错误;
故选:.
5.解:由图象可知,
该函数的对称轴是直线,与轴交于点,
故时的的取值范围是,
故选:.
6.解:(1)由图表中数据可得出:时,,所以二次函数开口向下,,故正确;
(2)又时,,所以,当时,,故正确;
(3)二次函数的对称轴为直线,
当时,的值随值的增大而减小,故错误;
(4),,为常数.且的图象与轴有两个交点,顶点坐标的纵坐标,
方程,
时,即是求的值,
由图象可知:有两个不相等的实数根,故正确;
故选:.
7.解:补图:由题可知,抛物线与的另一个交点应该在和之间,
①当时,①正确;
②对称轴,则,则,②错误;
③题目中只有顶点坐标出现字母,则一定跟顶点坐标的纵坐标有关,由顶点纵坐标,化简得,③正确;
④选项④的题意是抛物线与直线有两个交点,如图可知④正确;
综上所述,正确的结论为①③④,
故选:.
8.解:二次函数,
该函数的对称轴是直线,函数图象开口向上,当时取得最小值,
当时,,当时,,当时,,
,
故选:.
9.解:二次函数的图象上有且只有,,三点满足,
三点中必有一点在二次函数的顶点上,
,
二次函数的图象的顶点坐标为,
令,则,
解得或,
与轴的交点为,,
,
.
故选:.
10.解:二次函数解析式为,
抛物线的顶点坐标为,
当时,,解得,,
则抛物线与轴的交点为,,
把抛物线图象轴上方的部分沿轴翻折到轴下方,则翻折部分的抛物线解析式为,顶点坐标,
如图,当直线过点时,直线与该新图象恰好有三个公共点,
,解得;
当直线与抛物线相切时,直线与该新图象恰好有三个公共点,
即有相等的实数解,整理得,△,解得,
所以的值为或,
故选:.
二.填空题(共6小题)
11.解:由是二次函数,得
,
解得.
故答案为:.
12.解:将,代入二次函数得:
,
,
,
故答案为:.
13.解:由题意得:△
解得:,
故答案为:.
14.解:设:,则,
,
此函数的对称轴为:,
,故函数有最大值,
当时,函数取得最大值,
则:,
故:答案是144.
15.解:点在抛物线上,
,
,
当时,有最大值4.
故答案为:4.
16.解:二次函数,
该函数的对称轴为直线,
当时,随的增大而减小,且时,的最大值为7,
,当时,,
,
解得,,(舍去),
故答案为:.
三.解答题(共8小题)
17.解:(1)由题意得,,解得,,
则二次函数的解析式为;
(2)当时,,
点在这个二次函数的图象上.
18.解:(1)依题意,得,解得,
所求二次函数的解析式为:;
(2)
该抛物线的顶点坐标为,对称轴为直线,
列表:
0
1
2
3
4
0
1
0
描点画图得到的图象.
19.解:
(1),
顶点坐标为,对称轴为直线;
(2),抛物线开口向下,
对称轴为直线,
当时,随的增大而减小;
(3)
令,即,解得或
3
,抛物线开口向下,
当或时,;
当时,;
当或时,.
20.解:(1)设,
将、代入,得:,
解得:,
;
(2)
,
当时,取得最大值为1792,
答:售价为68元时获得最大利润,最大利润是1792元.
21.解:(1)抛物线与轴相交于,两点,
.
解得:.
故该抛物线解析式为;
(2)由抛物线解析式,可得,.
如图,过点作轴于点,交直线于,则点的横坐标是.
直线经过点,,
直线的解析式是.
把代入,得.
则.
.
.
22.解:(1)由排球运行的最大高度为28米,则顶点的坐标点为,则设抛物线的解析式为
点坐标为,点在抛物线上
解得
则排球飞行的高度(单位:米)与水平距离(单位:米)之间的函数关系式:
(2)当时,
当时,,故这次发球可以过网且不出边界
(3)设抛物线的解析式为:,
将点代入得:,即
此时抛物线的解析式为
根据题意,不过边界时有:,解得
要使网球过网:,解得
故李明同学发球要想过网,又使排球不会出界(排球压线属于没出界)二次函数中二次项系数的最大值为
23.解:(1)二次函数的图象经过点,,
,
解得:,
抛物线解析式为;
,
顶点坐标为.
(2)抛物线上存在点,使,如图,
①当点是抛物线上与点对称的点时,则有,
点关于对称轴直线的对称点坐标为,
,
②当直线时,则有,
设直线的解析式为,
,,
,
解得:,
直线的解析式为,
直线的解析式中一次项系数为,
设与平行的直线的解析式为,
将代入,得:,
解得:,
直线的解析式为,
联立抛物线解析式得:,
解得:,(舍去),
.
综上所述,,.
24.解:(1)将点、的坐标代入抛物线表达式得,解得:,
故抛物线的表达式为:①,
将点的坐标代入直线的表达式得:,解得:,
故直线的表达式为:②;
(2)设点的坐标为,
点的纵坐标与点的纵坐标相同,
将点的纵坐标代入得:,
解得:,
故点,,
则,
,故有最大值,当时,的最大值为;
(3)设点,则③,点,
①当为边时,
点向右平移2个单位得到,同样点向右平移2个单位得到,
即且④,
联立③④并解得:(舍去)或1或,
故点的坐标为或,或,;
②当为对角线时,
由中点公式得:且⑤,
联立③⑤并解得:(舍去)或1,故点;
综上,点的坐标为或,或,.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
浙教版2021年九年级(上)第一章《二次函数》专题训练
满分:120分
测试时间:120分钟
一.选择题(共10小题,每题3分,共30分)
1.下列函数中是二次函数的是
A.
B.
C.
D.
2.二次函数有
A.最大值
B.最小值
C.最大值7
D.最小值7
3.二次函数的顶点是
A.
B.
C.
D.
4.已知抛物线,则下列说法,错误的是
A.开口方向向下
B.顶点坐标是
C.对称轴是直线
D.当时,随的增大而减小
5.如图,二次函数使得的的取值范围是
A.或
B.
C.或
D.
6.二次函数,,是常数,且中的与的部分对应值如表所示,则下列结论中,正确的个数有
0
1
3
3
5
3
(1);(2)当时,;(3)当时,的值随值的增大而增大;
(4)方程有两个不相等是实数根.
A.4个
B.3个
C.2个
D.1个
7.如图是抛物线的部分图象,其顶点坐标为,且与轴的一个交点在点和之间,则下列结论中,其中正确的结论的个数是
①;②;③;④一元二次方程有两个不等实数根.
A.1
B.2
C.3
D.4
8.已知二次函数,当时,,则的值是
A.3
B.4
C.6
D.7
9.已知二次函数的图象交轴于,两点.若其图象上有且只有,,三点满足,则的值是
A.1
B.
C.2
D.4
10.将二次函数的图象在轴上方的部分沿轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,的值为
A.或
B.或
C.或
D.或
二.填空题(共6小题,每题4分,共24分)
11.若是二次函数,则 .
12.已知、是二次函数图象上的两个点,则与的大小关系为
.
13.若二次函数的图象与轴有两个不相同的交点,则的取值范围是
.
14.在综合实践活动中,同学们借助如图所示的直角墙角(两边足够长),用长的篱笆围成一个矩形花园,则矩形花园的最大面积为
.
15.已知抛物线,点在抛物线上,则的最大值是
.
16.已知二次函数(其中是自变量),当时,随的增大而减小,且时,的最大值为7,则的值为
.
三.解答题(共8小题,共66分)
17.(6分)已知二次函数的图象经过点,.
(1)试确定此二次函数的解析式;
(2)请你判断点是否在这个二次函数的图象上?
18.(6分)已知二次函数的图象经过点,.
(1)求该二次函数的解析式;
(2)在图中画出该函数的图象.
19.(6分)抛物线.
(1)
用配方法求顶点坐标,
对称轴;
(2)取何值时,随的增大而减小?
(3)取何值时,;取何值时,;取何值时,.
20.(8分)2019年春节期间某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于68元,经市场调查,每天的销售量(千克)与每千克售价(元满足一次函数关系,部分数据如下表:
售价(元千克)
50
55
60
销售量(千克)
100
90
80
(1)则与之间的函数表达式
.
(2)设这种商品每天的利润为(元,求与之间的函数表达式,并求出当售价为多少元时获得最大利润,最大利润是多少?(利润收入成本)
21.(8分)如图,抛物线与轴相交于,两点,其中顶点为.
(1)求该抛物线的解析式;
(2)若该抛物线与轴的交点为,求的面积.
22.(10分)如图,已知女排球场的长度为18米,位于球场中线处的球网的高度2.24米,一队员站在点处发球,排球从点的正上方2米的点向正前方飞去,排球的飞行路线是抛物线的一部分,当排球运行至离点的水平距离为6米时,到达最高点,以为原点建立如图所示的平面直角坐标系.
(1)若排球运行的最大高度为2.8米,求排球飞行的高度(单位:米)与水平距离(单位:米)之间的函数关系式(不要求写自变量的取值范围);
(2)在(1)的条件下,这次所发的球能够过网吗?如果能够过网,是否会出界?请说明理由;
(3)若李明同学发球要想过网,又使排球不会出界(排球压线属于没出界)求二次函数中二次项系数的最大值.
23.(10分)如图,已知二次函数的图象经过点,,与轴交于点.
(1)求抛物线的解析式;并写出抛物线的顶点坐标.
(2)抛物线上是否存在点,使,若存在,请求出点的坐标;若不存在,请说明理由.
24.(12分)已知,抛物线与轴交点为和点,与轴交点为,直线与抛物线的交点为点和点.
(1)求抛物线和直线的解析式;
(2)如图,点为抛物线上一动点(不与、重合),当点在直线下方时,过点作轴交于点,求的最大值;
(3)点为抛物线上一动点(不与、重合),为直线上一动点,是否存在点,使得以、、、为顶点的四边形是平行四边形?如果存在,请直接写出点的坐标,如果不存在,请说明理由.
参考答案与试题解析
一.选择题(共10小题)
1.解:二次函数的解析式为,
.,自变量的最高次数是二次,是二次函数;
.,自变量的最高次数是一次,不是二次函数;
,自变量的的次数为次,不是二次函数;
,自变量的的次数为次,不是二次函数.
故选:.
2.解:二次函数中,,
二次函数,当时有最大值,
故选:.
3.解:二次函数,
该函数的顶点坐标为,
故选:.
4.解:、抛物线,,抛物线开口向下,此选项正确;
、抛物线顶点坐标是,此选项正确;
、抛物线对称轴,此选项正确.
、抛物线的对称轴为,开口向下,当时,随的增大而增大,此选项错误;
故选:.
5.解:由图象可知,
该函数的对称轴是直线,与轴交于点,
故时的的取值范围是,
故选:.
6.解:(1)由图表中数据可得出:时,,所以二次函数开口向下,,故正确;
(2)又时,,所以,当时,,故正确;
(3)二次函数的对称轴为直线,
当时,的值随值的增大而减小,故错误;
(4),,为常数.且的图象与轴有两个交点,顶点坐标的纵坐标,
方程,
时,即是求的值,
由图象可知:有两个不相等的实数根,故正确;
故选:.
7.解:补图:由题可知,抛物线与的另一个交点应该在和之间,
①当时,①正确;
②对称轴,则,则,②错误;
③题目中只有顶点坐标出现字母,则一定跟顶点坐标的纵坐标有关,由顶点纵坐标,化简得,③正确;
④选项④的题意是抛物线与直线有两个交点,如图可知④正确;
综上所述,正确的结论为①③④,
故选:.
8.解:二次函数,
该函数的对称轴是直线,函数图象开口向上,当时取得最小值,
当时,,当时,,当时,,
,
故选:.
9.解:二次函数的图象上有且只有,,三点满足,
三点中必有一点在二次函数的顶点上,
,
二次函数的图象的顶点坐标为,
令,则,
解得或,
与轴的交点为,,
,
.
故选:.
10.解:二次函数解析式为,
抛物线的顶点坐标为,
当时,,解得,,
则抛物线与轴的交点为,,
把抛物线图象轴上方的部分沿轴翻折到轴下方,则翻折部分的抛物线解析式为,顶点坐标,
如图,当直线过点时,直线与该新图象恰好有三个公共点,
,解得;
当直线与抛物线相切时,直线与该新图象恰好有三个公共点,
即有相等的实数解,整理得,△,解得,
所以的值为或,
故选:.
二.填空题(共6小题)
11.解:由是二次函数,得
,
解得.
故答案为:.
12.解:将,代入二次函数得:
,
,
,
故答案为:.
13.解:由题意得:△
解得:,
故答案为:.
14.解:设:,则,
,
此函数的对称轴为:,
,故函数有最大值,
当时,函数取得最大值,
则:,
故:答案是144.
15.解:点在抛物线上,
,
,
当时,有最大值4.
故答案为:4.
16.解:二次函数,
该函数的对称轴为直线,
当时,随的增大而减小,且时,的最大值为7,
,当时,,
,
解得,,(舍去),
故答案为:.
三.解答题(共8小题)
17.解:(1)由题意得,,解得,,
则二次函数的解析式为;
(2)当时,,
点在这个二次函数的图象上.
18.解:(1)依题意,得,解得,
所求二次函数的解析式为:;
(2)
该抛物线的顶点坐标为,对称轴为直线,
列表:
0
1
2
3
4
0
1
0
描点画图得到的图象.
19.解:
(1),
顶点坐标为,对称轴为直线;
(2),抛物线开口向下,
对称轴为直线,
当时,随的增大而减小;
(3)
令,即,解得或
3
,抛物线开口向下,
当或时,;
当时,;
当或时,.
20.解:(1)设,
将、代入,得:,
解得:,
;
(2)
,
当时,取得最大值为1792,
答:售价为68元时获得最大利润,最大利润是1792元.
21.解:(1)抛物线与轴相交于,两点,
.
解得:.
故该抛物线解析式为;
(2)由抛物线解析式,可得,.
如图,过点作轴于点,交直线于,则点的横坐标是.
直线经过点,,
直线的解析式是.
把代入,得.
则.
.
.
22.解:(1)由排球运行的最大高度为28米,则顶点的坐标点为,则设抛物线的解析式为
点坐标为,点在抛物线上
解得
则排球飞行的高度(单位:米)与水平距离(单位:米)之间的函数关系式:
(2)当时,
当时,,故这次发球可以过网且不出边界
(3)设抛物线的解析式为:,
将点代入得:,即
此时抛物线的解析式为
根据题意,不过边界时有:,解得
要使网球过网:,解得
故李明同学发球要想过网,又使排球不会出界(排球压线属于没出界)二次函数中二次项系数的最大值为
23.解:(1)二次函数的图象经过点,,
,
解得:,
抛物线解析式为;
,
顶点坐标为.
(2)抛物线上存在点,使,如图,
①当点是抛物线上与点对称的点时,则有,
点关于对称轴直线的对称点坐标为,
,
②当直线时,则有,
设直线的解析式为,
,,
,
解得:,
直线的解析式为,
直线的解析式中一次项系数为,
设与平行的直线的解析式为,
将代入,得:,
解得:,
直线的解析式为,
联立抛物线解析式得:,
解得:,(舍去),
.
综上所述,,.
24.解:(1)将点、的坐标代入抛物线表达式得,解得:,
故抛物线的表达式为:①,
将点的坐标代入直线的表达式得:,解得:,
故直线的表达式为:②;
(2)设点的坐标为,
点的纵坐标与点的纵坐标相同,
将点的纵坐标代入得:,
解得:,
故点,,
则,
,故有最大值,当时,的最大值为;
(3)设点,则③,点,
①当为边时,
点向右平移2个单位得到,同样点向右平移2个单位得到,
即且④,
联立③④并解得:(舍去)或1或,
故点的坐标为或,或,;
②当为对角线时,
由中点公式得:且⑤,
联立③⑤并解得:(舍去)或1,故点;
综上,点的坐标为或,或,.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
