浙教版九上 2.4 二次函数的应用(3) 课件
文档属性
| 名称 | 浙教版九上 2.4 二次函数的应用(3) 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 80.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-08-05 16:15:41 | ||
图片预览


文档简介
(共11张PPT)
浙教版九年级《数学》上册
二次函数的图象与x轴有没有交点,由什么决定
复习思考
由b -4ac的符号决定
b -4ac﹥0,有两个交点
b -4ac=0,只有一个交点
b -4ac﹤0,没有交点
求出二次函数y=10x-5x 图象的顶点坐标,与x轴的交点坐标,并画出函数的大致图象。
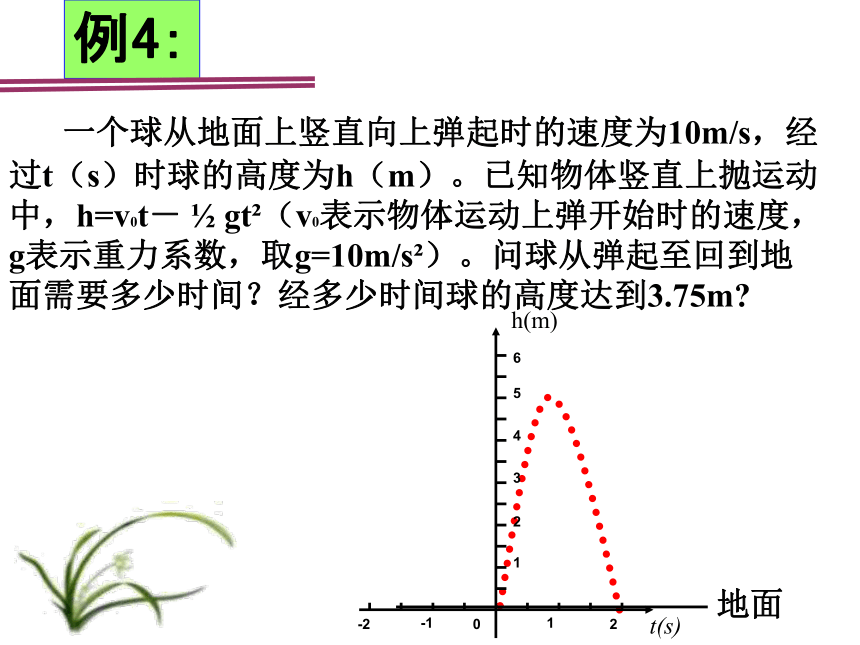
例4:
一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- gt (v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s )。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
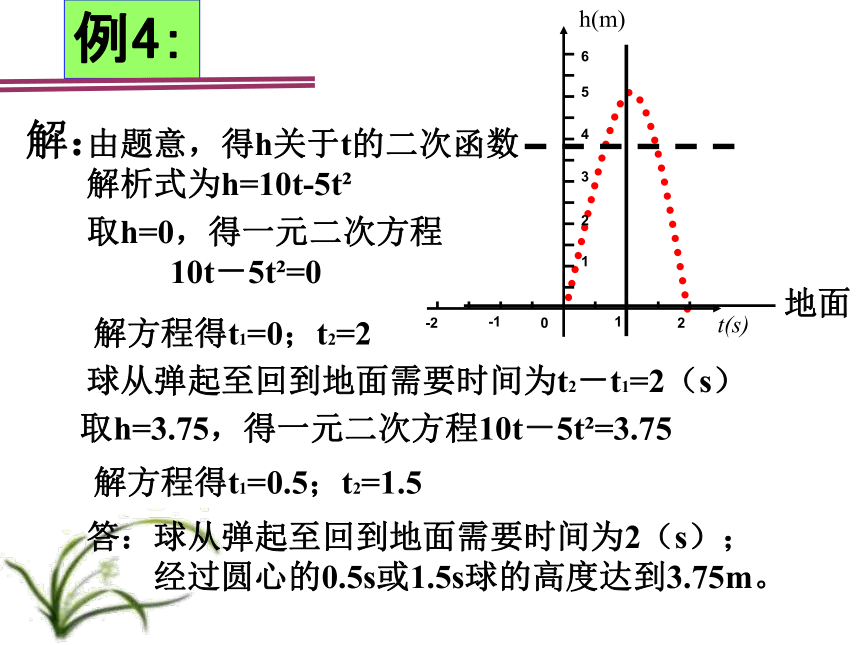
例4:
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t
取h=0,得一元二次方程
10t-5t =0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t =3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
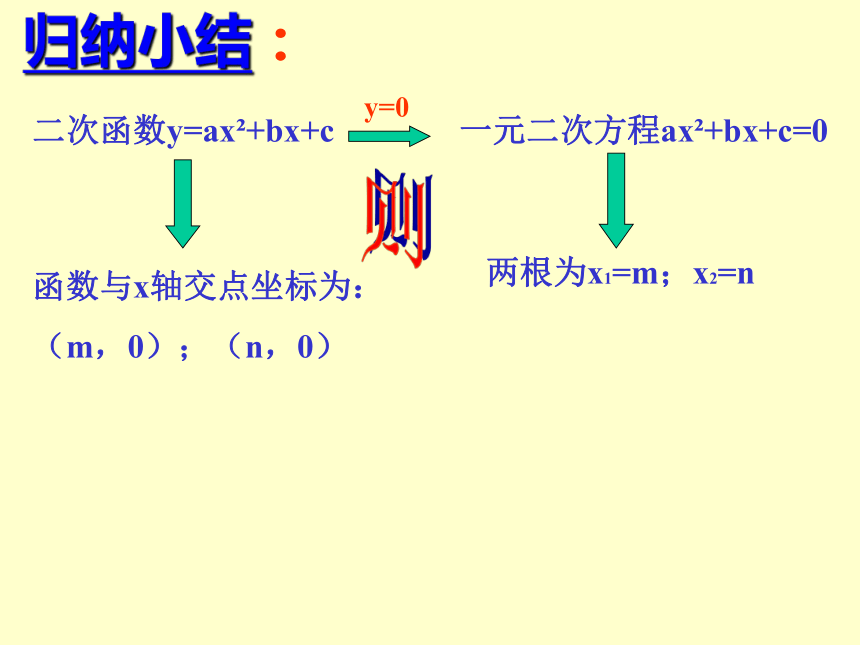
二次函数y=ax +bx+c
归纳小结:
y=0
一元二次方程ax +bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
课内练习:
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为 30m 时,达到最
大高10m。
⑴ 求球运动路线的函数解析式和自变量的取值范围;
⑵ 求球被抛出多远;
⑶ 当球的高度为5m时,球离抛出地面的水平距离
是多少m?
40
50
30
20
10
x
5
10
15
y
反过来,也可利用二次函数的图象
求一元二次方程的解。
二次函数y=ax +bx+c
归纳小结:
y=0
一元二次方程ax +bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
利用二次函数的图象求一元二次方程
X +X-1= 0 的近似解。
例5:
1
2
0
-1
-2
x
1
2
3
4
5
6
y
做一做:
◆用求根公式求出方程x +x-1=0的近似解,并由检验例5中所给图象解法的精确度。
◆利用函数图象判断下列方程有没有解,有几个解。若有解,求出它们的解(精确到0.1)。
①X =2x-1 ②2x -x+1=0 ③2x -4x-1=0
在本节的例5中,我们把一元二次方程X +X-1= 0 的解看做是抛物线y=x +x-1与x轴交点的横坐标,利用图象求出了方程的近似解。如果把方程x +x-1 = 0变形成 x = -x+1,那么方程的解也可以看成怎样的两个函数的交点的横坐标?用不同图象解法试一试,结果相同吗?在不使用计算机画图象的情况下,你认为哪一种方法较为方便?
探究活动:
1、通过这节课的学习活动你有哪些收获?
2、对这节课的学习,你还有什么想法吗?
浙教版九年级《数学》上册
二次函数的图象与x轴有没有交点,由什么决定
复习思考
由b -4ac的符号决定
b -4ac﹥0,有两个交点
b -4ac=0,只有一个交点
b -4ac﹤0,没有交点
求出二次函数y=10x-5x 图象的顶点坐标,与x轴的交点坐标,并画出函数的大致图象。
例4:
一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- gt (v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s )。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
例4:
地面
1
2
0
-1
-2
t(s)
1
2
3
4
5
6
h(m)
解:
由题意,得h关于t的二次函数
解析式为h=10t-5t
取h=0,得一元二次方程
10t-5t =0
解方程得t1=0;t2=2
球从弹起至回到地面需要时间为t2-t1=2(s)
取h=3.75,得一元二次方程10t-5t =3.75
解方程得t1=0.5;t2=1.5
答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
二次函数y=ax +bx+c
归纳小结:
y=0
一元二次方程ax +bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
课内练习:
1、一球从地面抛出的运动路线呈抛物线,如图,
当球离抛出地的水平距离为 30m 时,达到最
大高10m。
⑴ 求球运动路线的函数解析式和自变量的取值范围;
⑵ 求球被抛出多远;
⑶ 当球的高度为5m时,球离抛出地面的水平距离
是多少m?
40
50
30
20
10
x
5
10
15
y
反过来,也可利用二次函数的图象
求一元二次方程的解。
二次函数y=ax +bx+c
归纳小结:
y=0
一元二次方程ax +bx+c=0
两根为x1=m;x2=n
函数与x轴交点坐标为:
(m,0);(n,0)
利用二次函数的图象求一元二次方程
X +X-1= 0 的近似解。
例5:
1
2
0
-1
-2
x
1
2
3
4
5
6
y
做一做:
◆用求根公式求出方程x +x-1=0的近似解,并由检验例5中所给图象解法的精确度。
◆利用函数图象判断下列方程有没有解,有几个解。若有解,求出它们的解(精确到0.1)。
①X =2x-1 ②2x -x+1=0 ③2x -4x-1=0
在本节的例5中,我们把一元二次方程X +X-1= 0 的解看做是抛物线y=x +x-1与x轴交点的横坐标,利用图象求出了方程的近似解。如果把方程x +x-1 = 0变形成 x = -x+1,那么方程的解也可以看成怎样的两个函数的交点的横坐标?用不同图象解法试一试,结果相同吗?在不使用计算机画图象的情况下,你认为哪一种方法较为方便?
探究活动:
1、通过这节课的学习活动你有哪些收获?
2、对这节课的学习,你还有什么想法吗?
同课章节目录
