2.5 逆命题与逆定理 课件(共23张PPT)
文档属性
| 名称 | 2.5 逆命题与逆定理 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-10 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
2.5逆命题和逆定理
浙教版 八年级上
新知导入
对某一件事情作出正确或不正确的判断的句子叫做命题.
命题的概念:
命题:“平行四边形的对角线互相平分”
条件是__________________________,
结论是_____________________ .
命题:“对角线互相平分的四边形是平行四边形” 条件是__________________________________,结论是__________________________.
条件和结论,它的一般形式是“如果……,那么……”
命题的结构:
有一个四边形是平行四边形
它的对角线互相平分
有一个四边形的对角线互相平分
这个四边形是平行四边形
新知导入
思考:
命题有真有假.
正确的命题是真命题,错误的命题是假命题.
“飞机是会飞的交通工具”
“会飞的交通工具是飞机”
这两个命题有什么不同?它们都是真命题吗?
第一个命题的条件是第二个命题的结论,第二个命题的结论是第一个命题的条件
探究思考
假
a=b
a2=b2
(4)如果a2=b2,那么a=b.
真
a2=b2
a=b
(3)如果a=b,那么a2=b2.
真
两直线平行
同位角相等
(2)同位角相等,两直线平行
真
同位角相等
两直线平行
(1)两直线平行,同位角相等
真假
结论
条件
填表并思考:命题(1)和命题(2),命题(3)和命题(4)的条件和结论有什么关系?
(1)的条件是(2)的结论,(2)的结论是(1)的条件;(3)的条件是(4)的结论,(4)的结论是(3)的条件
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
我们把其中的一个叫做原命题,另一个叫做它的逆命题.
上表中,命题(1)与命题(2),命题(3)与命题(4)都是互逆命题.
每个命题都有它的逆命题,但每个真命题的逆命题是否一定为真命题?
不一定
如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫互逆定理.
知识讲解
下列定理中,哪些有逆定理?如果有逆定理,请写出它的逆定理.
(1) 两边及其夹角对应相等的两个三角形全等;
(2) 成轴对称的两个图形是全等图形;
(3) 等腰三角形顶角的平分线与底边上的高线互相重合.
解:(1) 有逆定理.如果两个三角形全等,那么这两个三
角形对应的两边及其夹角相等
(2) 无逆定理
(3) 有逆定理.若一个三角形的一个角的平分线与这个
角所对边上的高线互相重合,则这个三角形是等腰
三角形.
做一做
例题讲解
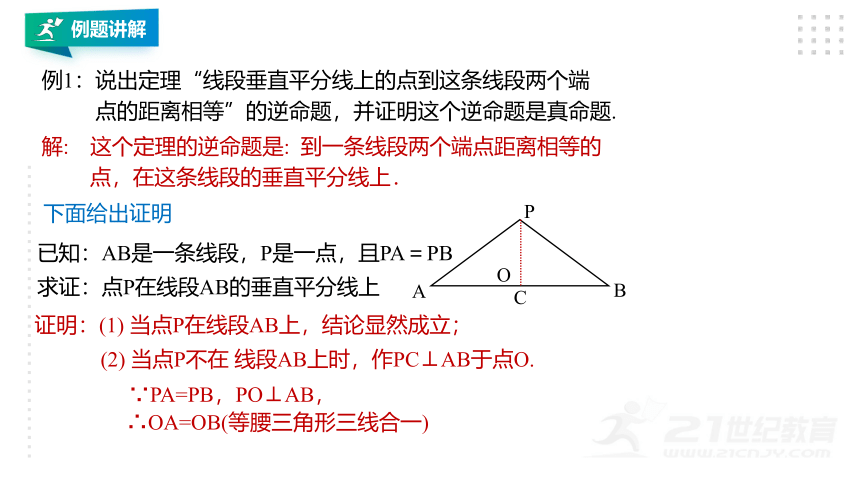
例1:说出定理“线段垂直平分线上的点到这条线段两个端
点的距离相等”的逆命题,并证明这个逆命题是真命题.
解: 这个定理的逆命题是: 到一条线段两个端点距离相等的
点,在这条线段的垂直平分线上.
P
A
B
已知:AB是一条线段,P是一点,且PA=PB
求证:点P在线段AB的垂直平分线上
(2) 当点P不在 线段AB上时,作PC⊥AB于点O.
O
C
证明:(1) 当点P在线段AB上,结论显然成立;
∵PA=PB,PO⊥AB,
∴OA=OB(等腰三角形三线合一)
下面给出证明
∴PC是AB的垂直平分线.
∴点P在线段AB的垂直平行线上
可见,线段垂直平分线性质定理的逆定理是真命题.
线段垂直平分线性质定理的逆定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
例题讲解
例2:写出命题“两个全等三角形的面积相等”的逆命题,
判断这个命题的真假,并给出证明.
解:逆命题是 “ 如果两个三角形的面积相等,那么这两个
三角形全等”.
这个逆命题是假命题. 举反例如下:
如图,在△ABC和△ABE中,CD,EF分别是△ABC和△ABE的AB边上的高线,且CD=EF,则△ABC和△ABE的面积相等,但显然它们不全等. 所以这个逆命题是假命题.
C
D
A
E
B
F
当堂练习
定理“直角三角形斜边上的中线等于斜边的一半”的逆命题是______,这个命题正确吗?若正确,请你证明这个命题,若不正确请说明理由.
逆命题是“三角形一边上的中线是这边的一半的话,那么这个三角形是直角三角形”
这个命题是正确的.
已知:△ABC中,D是AC的中点,BD=AD,BD=DC.
求证:△ABC是直角三角形.
A
C
D
B
证明:∵BD=AD,
∴∠A=∠ABD,
∵BD=DC,
∴∠C=∠DBC,
∵∠A+∠C+∠ABD+∠DBC=180°,
∴2(∠A+∠C)=180°,
解得∠A+∠C=90°,
∴∠ABC=90°.
即△ABC是直角三角形.
21cnjy.com
A
C
D
B
课堂小结
这节课我们学习了:
1. 逆命题、逆定理的定义.
2. 互逆命题的定义.
3. 线段的垂直平分线性质定理的逆定理的证明以及运用.
课堂练习
(1)下列命题的逆命题是真命题的有( )
①四边形是多边形;②两直线平行,同旁内角互补;
③若ab=0,则a=0或b=0;④三角形中等角对等边.
A. 1个 B. 2个 C. 3个 D. 4个
(1) 其逆命题是:多边形是四边形,错误;
(2) 其逆命题是:如果同旁内角互补,则两直线平行,正确;
(3) 其逆命题是:若a=0或b=0,则ab=0,正确;
(4) 其逆命题是:三角形中等边对等角,正确.
所以真命题的有三个.
故选C.
C
1. 选择题
课堂练习
A. 任何命题都有逆命题,正确,故本选项错误;
B. 任何定理不一定都有逆定理,故本选项正确;
C. 真命题的逆命题不一定为真,正确,故本选项错误;
D. 任何命题都是由条件和结论构成的,正确,故本选项错误.
故选B.
(2) 下列说法错误的是( )
A. 任何命题都有逆命题
B. 任何定理都有逆定理
C. 真命题的逆命题不一定为真
D. 任何命题都是由条件和结论构成的
B
课堂练习
(3) 对于以下说法:①如果一个命题是真命题,那么它的逆命题不一定是真命题;②每个定理都有逆定理;③基本事实是通过推理判断为正确的命题;④“同位角相等”是定理.其中正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
A
课堂练习
2. 写出下列各命题的逆命题,并判断其逆命题是真命题还是假命题,若是假命题,请举反例说明.
(1) 两直线平行,同位角相等;
(2) 垂直于同一条直线的两直线平行;
(3) 相等的角是内错角;
(4) 有一个角是60°的三角形是等边三角形.
解:同位角相等,两直线平行;真命题
解:如果两条直线平行,那么这两条直线垂直于同一
条直线;真命题
解:内错角相等;假命题,举反例略
解:等边三角形有一个角是60°;真命题
课堂练习
3. 写出符合下列条件的一个原命题
(1) 原命题和逆命题都是真命题;
(2) 原命题是假命题,但逆命题是真命题;
(3) 原命题是真命题,但逆命题是假命题;
(4) 原命题和逆命题都是假命题;
答案不唯一
(1) 若x=0或x =1,则x ( x -1)=0
(2) 若x ( x -1)=0,则x=0
(3) 若x=0,则x ( x -1)=0
(4) 若x=0,则x-1=0
4. 说出命题“等腰三角形两腰上的高相等”的逆命题,并判断逆命题的真假. 若逆命题是真命题,请加以证明;若逆命题是假命题,请举出反例.
逆命题是:如果一个三角形两边上的高相等,则这个三角形是等腰三角形.
此逆命题是真命题证明如下:
已知:如图,在ABC中,BE⊥AC于E,CF⊥AB于F,且BE=CF
求证:AB=AC.
证明:∵S△ABC= AB · CF= AC·BE,而BE=CF,
∴AB=AC,
∴△ABC是等腰三角形.
A
C
B
F
E
5. 写出命题“如果一个三角形是直角三角形,那么它的两个锐角的角平分线所夹的锐角是45°“的逆命题,并证明这个命题是真命题.
逆命题是:如果一个三角形的两个角的角平分线所夹的锐角是45°,那么这个三角是直角三角形.
已知:如图,△ABC中,BE是∠ABC的角平分线,交AC于E,
AD是∠CAB的角平分线,交BC于D,BE和AD相交
于O点,且∠EOA=45°.
求证:△ABC是直角三角形
A
B
C
D
E
O
21cnjy.com
证明:∵BE是∠ABC的角平分线,AD是∠CAB的角平分线,
∴∠OAB= ∠CAB,∠OBA= ∠CBA,
∴ ∠OAB+∠OBA= (∠CAB+∠CBA),
∴180°-∠AOB= (180-∠C),
∴∠AOB=90°+ ∠C
又∵∠EOA=45°,
∴∠AOB=135°=90°+ ∠C ,
∴∠C=90°,
∴△ABC是直角三角形.
A
B
C
D
E
O
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
2.5逆命题和逆定理
浙教版 八年级上
新知导入
对某一件事情作出正确或不正确的判断的句子叫做命题.
命题的概念:
命题:“平行四边形的对角线互相平分”
条件是__________________________,
结论是_____________________ .
命题:“对角线互相平分的四边形是平行四边形” 条件是__________________________________,结论是__________________________.
条件和结论,它的一般形式是“如果……,那么……”
命题的结构:
有一个四边形是平行四边形
它的对角线互相平分
有一个四边形的对角线互相平分
这个四边形是平行四边形
新知导入
思考:
命题有真有假.
正确的命题是真命题,错误的命题是假命题.
“飞机是会飞的交通工具”
“会飞的交通工具是飞机”
这两个命题有什么不同?它们都是真命题吗?
第一个命题的条件是第二个命题的结论,第二个命题的结论是第一个命题的条件
探究思考
假
a=b
a2=b2
(4)如果a2=b2,那么a=b.
真
a2=b2
a=b
(3)如果a=b,那么a2=b2.
真
两直线平行
同位角相等
(2)同位角相等,两直线平行
真
同位角相等
两直线平行
(1)两直线平行,同位角相等
真假
结论
条件
填表并思考:命题(1)和命题(2),命题(3)和命题(4)的条件和结论有什么关系?
(1)的条件是(2)的结论,(2)的结论是(1)的条件;(3)的条件是(4)的结论,(4)的结论是(3)的条件
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
我们把其中的一个叫做原命题,另一个叫做它的逆命题.
上表中,命题(1)与命题(2),命题(3)与命题(4)都是互逆命题.
每个命题都有它的逆命题,但每个真命题的逆命题是否一定为真命题?
不一定
如果一个定理的逆命题能被证明是真命题,那么就叫它是原定理的逆定理,这两个定理叫互逆定理.
知识讲解
下列定理中,哪些有逆定理?如果有逆定理,请写出它的逆定理.
(1) 两边及其夹角对应相等的两个三角形全等;
(2) 成轴对称的两个图形是全等图形;
(3) 等腰三角形顶角的平分线与底边上的高线互相重合.
解:(1) 有逆定理.如果两个三角形全等,那么这两个三
角形对应的两边及其夹角相等
(2) 无逆定理
(3) 有逆定理.若一个三角形的一个角的平分线与这个
角所对边上的高线互相重合,则这个三角形是等腰
三角形.
做一做
例题讲解
例1:说出定理“线段垂直平分线上的点到这条线段两个端
点的距离相等”的逆命题,并证明这个逆命题是真命题.
解: 这个定理的逆命题是: 到一条线段两个端点距离相等的
点,在这条线段的垂直平分线上.
P
A
B
已知:AB是一条线段,P是一点,且PA=PB
求证:点P在线段AB的垂直平分线上
(2) 当点P不在 线段AB上时,作PC⊥AB于点O.
O
C
证明:(1) 当点P在线段AB上,结论显然成立;
∵PA=PB,PO⊥AB,
∴OA=OB(等腰三角形三线合一)
下面给出证明
∴PC是AB的垂直平分线.
∴点P在线段AB的垂直平行线上
可见,线段垂直平分线性质定理的逆定理是真命题.
线段垂直平分线性质定理的逆定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
例题讲解
例2:写出命题“两个全等三角形的面积相等”的逆命题,
判断这个命题的真假,并给出证明.
解:逆命题是 “ 如果两个三角形的面积相等,那么这两个
三角形全等”.
这个逆命题是假命题. 举反例如下:
如图,在△ABC和△ABE中,CD,EF分别是△ABC和△ABE的AB边上的高线,且CD=EF,则△ABC和△ABE的面积相等,但显然它们不全等. 所以这个逆命题是假命题.
C
D
A
E
B
F
当堂练习
定理“直角三角形斜边上的中线等于斜边的一半”的逆命题是______,这个命题正确吗?若正确,请你证明这个命题,若不正确请说明理由.
逆命题是“三角形一边上的中线是这边的一半的话,那么这个三角形是直角三角形”
这个命题是正确的.
已知:△ABC中,D是AC的中点,BD=AD,BD=DC.
求证:△ABC是直角三角形.
A
C
D
B
证明:∵BD=AD,
∴∠A=∠ABD,
∵BD=DC,
∴∠C=∠DBC,
∵∠A+∠C+∠ABD+∠DBC=180°,
∴2(∠A+∠C)=180°,
解得∠A+∠C=90°,
∴∠ABC=90°.
即△ABC是直角三角形.
21cnjy.com
A
C
D
B
课堂小结
这节课我们学习了:
1. 逆命题、逆定理的定义.
2. 互逆命题的定义.
3. 线段的垂直平分线性质定理的逆定理的证明以及运用.
课堂练习
(1)下列命题的逆命题是真命题的有( )
①四边形是多边形;②两直线平行,同旁内角互补;
③若ab=0,则a=0或b=0;④三角形中等角对等边.
A. 1个 B. 2个 C. 3个 D. 4个
(1) 其逆命题是:多边形是四边形,错误;
(2) 其逆命题是:如果同旁内角互补,则两直线平行,正确;
(3) 其逆命题是:若a=0或b=0,则ab=0,正确;
(4) 其逆命题是:三角形中等边对等角,正确.
所以真命题的有三个.
故选C.
C
1. 选择题
课堂练习
A. 任何命题都有逆命题,正确,故本选项错误;
B. 任何定理不一定都有逆定理,故本选项正确;
C. 真命题的逆命题不一定为真,正确,故本选项错误;
D. 任何命题都是由条件和结论构成的,正确,故本选项错误.
故选B.
(2) 下列说法错误的是( )
A. 任何命题都有逆命题
B. 任何定理都有逆定理
C. 真命题的逆命题不一定为真
D. 任何命题都是由条件和结论构成的
B
课堂练习
(3) 对于以下说法:①如果一个命题是真命题,那么它的逆命题不一定是真命题;②每个定理都有逆定理;③基本事实是通过推理判断为正确的命题;④“同位角相等”是定理.其中正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
A
课堂练习
2. 写出下列各命题的逆命题,并判断其逆命题是真命题还是假命题,若是假命题,请举反例说明.
(1) 两直线平行,同位角相等;
(2) 垂直于同一条直线的两直线平行;
(3) 相等的角是内错角;
(4) 有一个角是60°的三角形是等边三角形.
解:同位角相等,两直线平行;真命题
解:如果两条直线平行,那么这两条直线垂直于同一
条直线;真命题
解:内错角相等;假命题,举反例略
解:等边三角形有一个角是60°;真命题
课堂练习
3. 写出符合下列条件的一个原命题
(1) 原命题和逆命题都是真命题;
(2) 原命题是假命题,但逆命题是真命题;
(3) 原命题是真命题,但逆命题是假命题;
(4) 原命题和逆命题都是假命题;
答案不唯一
(1) 若x=0或x =1,则x ( x -1)=0
(2) 若x ( x -1)=0,则x=0
(3) 若x=0,则x ( x -1)=0
(4) 若x=0,则x-1=0
4. 说出命题“等腰三角形两腰上的高相等”的逆命题,并判断逆命题的真假. 若逆命题是真命题,请加以证明;若逆命题是假命题,请举出反例.
逆命题是:如果一个三角形两边上的高相等,则这个三角形是等腰三角形.
此逆命题是真命题证明如下:
已知:如图,在ABC中,BE⊥AC于E,CF⊥AB于F,且BE=CF
求证:AB=AC.
证明:∵S△ABC= AB · CF= AC·BE,而BE=CF,
∴AB=AC,
∴△ABC是等腰三角形.
A
C
B
F
E
5. 写出命题“如果一个三角形是直角三角形,那么它的两个锐角的角平分线所夹的锐角是45°“的逆命题,并证明这个命题是真命题.
逆命题是:如果一个三角形的两个角的角平分线所夹的锐角是45°,那么这个三角是直角三角形.
已知:如图,△ABC中,BE是∠ABC的角平分线,交AC于E,
AD是∠CAB的角平分线,交BC于D,BE和AD相交
于O点,且∠EOA=45°.
求证:△ABC是直角三角形
A
B
C
D
E
O
21cnjy.com
证明:∵BE是∠ABC的角平分线,AD是∠CAB的角平分线,
∴∠OAB= ∠CAB,∠OBA= ∠CBA,
∴ ∠OAB+∠OBA= (∠CAB+∠CBA),
∴180°-∠AOB= (180-∠C),
∴∠AOB=90°+ ∠C
又∵∠EOA=45°,
∴∠AOB=135°=90°+ ∠C ,
∴∠C=90°,
∴△ABC是直角三角形.
A
B
C
D
E
O
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
