2.6.1直角三角形 (共26张PPT)

(共26张PPT)
2.6.1直角三角形
浙教版 八年级上
新知导入
日常生活中常见的直角三角形有哪些
这个图形中，你能从图中找出多少个直角三角形？
新知导入
知识讲解
直角边
直角边
斜边
A
C
B
直角三角形的定义：
有一个角是直角的三角形叫直角三角形．
直角三角形ABC用符号“Rt△ABC”表示.
探究发现
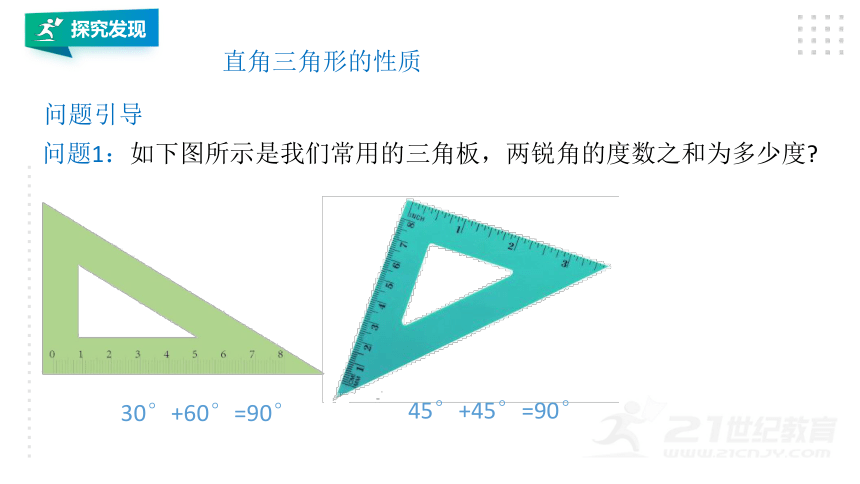
问题1：如下图所示是我们常用的三角板，两锐角的度数之和为多少度
30°+60°=90°
直角三角形的性质
问题引导
45°+45°=90°
探究发现
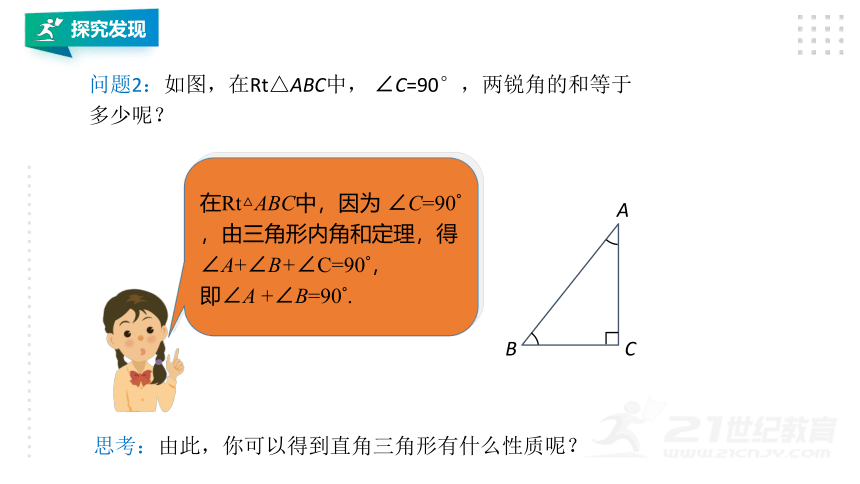
问题2：如图，在Rt△ABC中， ∠C=90°，两锐角的和等于多少呢？
在Rt△ABC中，因为 ∠C=90°，由三角形内角和定理，得∠A+∠B+∠C=90°，
即∠A +∠B=90°.
思考：由此，你可以得到直角三角形有什么性质呢？
A
C
B
A
B
C
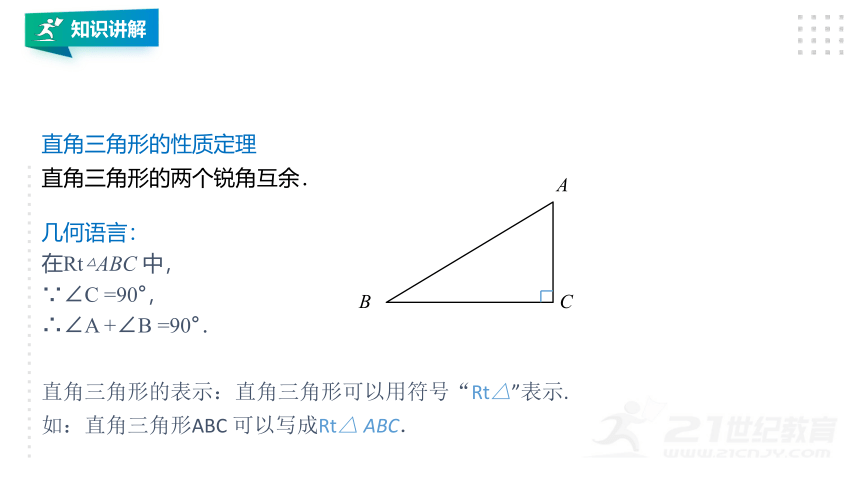
几何语言：
在Rt△ABC 中，
∵∠C =90°，
∴∠A +∠B =90°．　
直角三角形的两个锐角互余．　　
直角三角形的性质定理
直角三角形的表示：直角三角形可以用符号“Rt△”表示.
如：直角三角形ABC 可以写成Rt△ ABC．
知识讲解
例题讲解
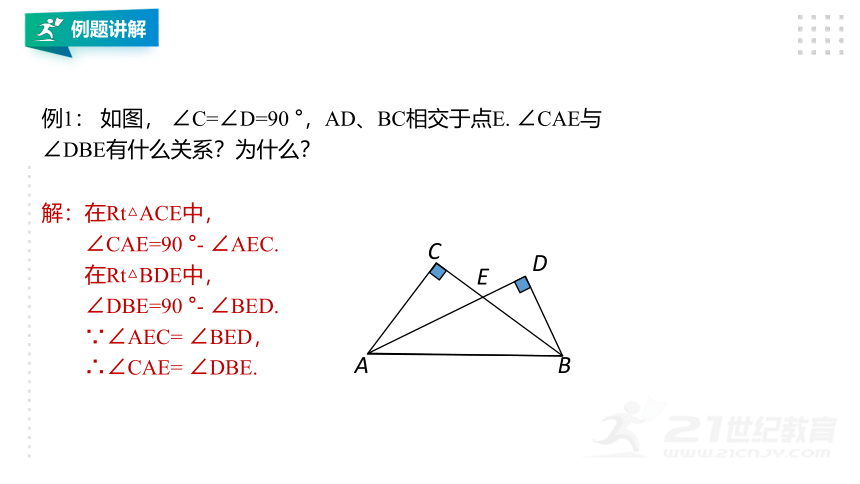
例1： 如图， ∠C=∠D=90 °，AD、BC相交于点E. ∠CAE与∠DBE有什么关系？为什么？
解：在Rt△ACE中，
∠CAE=90 °- ∠AEC.
在Rt△BDE中，
∠DBE=90 °- ∠BED.
∵∠AEC= ∠BED，
∴∠CAE= ∠DBE.
A
B
C
D
E
当堂练习
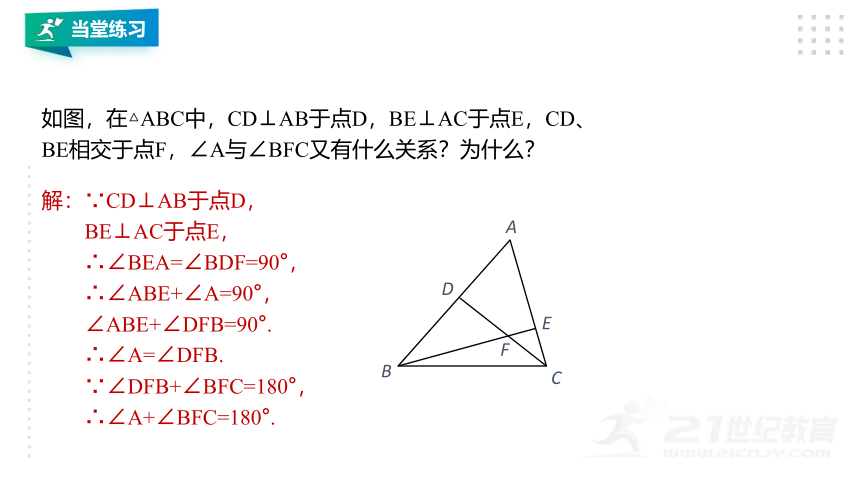
如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，CD、BE相交于点F，∠A与∠BFC又有什么关系？为什么？
解：∵CD⊥AB于点D，
BE⊥AC于点E，
∴∠BEA=∠BDF=90°，
∴∠ABE+∠A=90°，
∠ABE+∠DFB=90°.
∴∠A=∠DFB.
∵∠DFB+∠BFC=180°，
∴∠A+∠BFC=180°.
D
C
A
B
E
F
例2：一名滑雪运动员沿着倾斜角为30°的斜坡，从A滑行至B.
已知AB＝200m，问这名滑雪运动员的高度下降了多少m？
30°
A
C
B
D
例题讲解
解：如图，作Rt△ABC的斜边上的中线CD，则
CD=AD=0.5AB=0.5×200=100m
(直角三角形斜边上的中线等于斜边的一半)
∵∠B=300
∴∠A=900－∠B=900－300=600
(直角三角形的两个锐角互余)
∴△ADC是等边三角形
(有一个角是60°的等腰三角形是等边三角形)
∴AC=AD=100(m)
答:这名滑雪运动员的高度下降了100m.
例题讲解
A
B
C
在直角三角形中，30°角所对的直角边等于斜边的一半.
∵△ABC是直角三角形，∠B=30°
∴AC = AB
(在直角三角形中，30°角所对的直角边等于斜边的一半)
30°
知识讲解
证明：
延长BC到D，使CD等于BC，连结AD
∵BC=DC，∠ACB=∠ACD，AC=AC
∴△ACB≌△ACD(SAS)
∴∠ BAC=∠DAC=30°
∴∠BAD=60°
∴△ABD是等边三角形
∴AB=BD=2BC
D
C
A
B
课堂小结
1. 认识直角三角形.
直角三角形的最基本元素：直角.
2. 性质
(1) 直角三角形的两个锐角互余.
(2) 直角三角形斜边上的中线等于斜边的一半.
课堂练习
1. 选择.
(1) 在一个直角三角形中，有一个锐角等于40°，则另 一个锐角的度数是( )
A．40° B．50° C．60° D．70°
(2) 如图所示，△ABC为直角三角形，∠ACB=90°，CD⊥AB，与∠1互余的角有( )
A．∠B B．∠A
C．∠BCD和∠A D．∠BCD
B
C
A
C
B
D
1
课堂练习
2. 填空.
在Rt △ABC中，∠ACB=90 °
(1) 若∠B=75°，则 ∠A=___ °;
(2) 若∠A:∠B=3:2，则 ∠ A=____°， ∠B= ___°;
(3) 若CD是AB边上的高，图中有____对互余的角;
有___对相等的锐角.
15
54
36
4
2
∠A +∠1=90 °
∠A +∠B=90 °
∠2+∠1=90 °
∠2+∠B=90 °
A
C
B
D
1
2
课堂练习
(4) 如图：在Rt△ABC中∠A=30°，AB+BC=12cm，
则AB=_____cm.
(5) 如图：△ABC是等边三角形，AD⊥BC，DE⊥AB，
若AB=8cm，　BD= ，BE= .
8
4cm
2cm
Ｃ
Ｂ
Ａ
30°
A
C
E
B
D
课堂练习
3. 解答题.
(1) 如图1，∠B=∠C=90°，AD交BC于点O，∠A与∠D有什么关系？
解：方法一（利用平行的判定和性质）
∵∠B=∠C=90°，
∴AB∥CD，
∴∠A=∠D.
方法二（利用直角三角形的性质）
∵∠B=∠C=90°，
∴∠A+∠AOB=90°
（直角三角形的两个锐角互余）
∠D+∠COD=90°.
∵∠AOB=∠COD，
∴∠A=∠D.
图1
A
C
B
D
O
课堂练习
(2) 如图2，∠B=∠D=90°，AD交BC于点O，∠A与∠C有什么关系？请说明理由.
解：∠A=∠C.理由如下：
∵∠B=∠D=90°，
∴∠A+∠AOB=90°，
∠C+∠COD=90°.
∵∠AOB=∠COD，
∴∠A=∠C.
图2
与图1有哪些共同点与不同点？
A
C
B
D
O
4. 如图，CD是Rt△ABC斜边上的高，请找出图中各对互余的角.
解：∵CD⊥AB，
∴ △ACD、 △BCD都是Rt△，
已知△ABC是Rt△，
∴ ∠A与∠B， ∠A与∠ACD，
∠B与∠BCD互余．
(直角三角形的两个锐角互余)
又∵ ∠ACB＝90°
　∴ ∠ACD与∠BCD互余．
所以图中互余的角有4对：
∠A与∠B，∠A与∠ACD
∠B与∠BCD，∠ACD与∠BCD
A
C
B
D
课堂练习
5. 如图在△ABC中，AB=AC=2a，∠ABC=∠ACB=15°，CD是腰
AB上的高，求S△ABC.
解：∵∠ABC=∠ACB=15°
∴∠DAC=∠ABC+∠ACB=30°
∴ CD= AC=a
∴S△ABC= AB×CD= ×2a×a=a2
D
C
B
A
课堂练习
6. 如图，在Rt △ ABC与Rt △ ACE中，∠ABC=∠AEC=90 °，点M是AC边上的中点，连接BM、EM. 试判断BM，EM是否相等，并给出证明.
解：BM=EM
证明：∵ ∠ ABC= ∠ AEC=90 °
M是AC边上的中点.
∴ BM = AC，EM = AC
(直角三角形斜边上的中线等于斜边的一半)
∴ BM= EM
E
A
B
C
M
课堂练习
7. 如图，在Rt△ABC与Rt△ACE中，∠ABC=∠AEC=90 °，点M是AC的中点，连接BM、EM、BE.试判断△BME的形状，并说明理由.
解：△BME是等腰三角形.
理由：∵ ∠ ABC= ∠ AEC=90 °
M是AC边上的中点，
∴ BM= AC，BE= AC
(直角三角形斜边上的中线等于斜边的一半)
∴ BM= EM
∴ △BME是等腰三角形
A
C
B
E
M
课堂练习
作业布置
作业本
课本作业题3.4.5
https://www.21cnjy.com/help/help_extract.php